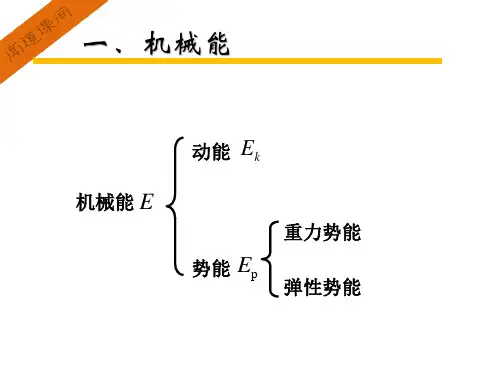
动能势能Ek+EP重力势能弹性势能

机械能守恒定律：机械能=动能+重力势能+弹性势能(条件:系统只有内部的重力或弹力做功). 守恒条件：(功角度)只有重力,弹力做功；(能转化角度)只发生动能与势能之间的相互转化。

“只有重力做功”不等于“只受重力作用”。

在该过程中，物体可以受其它力的作用，只要这些力不做功，或所做功的代数和为零，就可以认为是“只有重力做功”。

列式形式：E 1=E 2(先要确定零势面) P 减(或增)=E 增(或减) E A 减(或增)=E B 增(或减)mgh 1 +121212222mV mgh mV =+ 或者 ∆E p 减 = ∆E k 增5. 如图所示在一根细棒的中点C 和端点B ，分别固定两个质量、体积完全相同的小球，棒可以绕另一端A 在竖直平面内无摩擦地转动. 若从水平位置由静止释放，求两球到达最低位置时线速度的大小. 小球的质量为m ，棒的质量不计. 某同学对此题的解法是:设AB=L ，AC=L2，到最低位置时B 球和C 球的速度大小分别为v 1、v 2.运动过程中只有重力对小球做功，所以每个球的机械能都守恒.：C 球有21122Lmv mg =，1v (m/s) B 球有 2212m v m g L =,2v =(m/s) 你同意上述解法吗？若不同意，请简述理由并求出你认为正确的结果. 5. (10分)解： 不同意，因为在此过程中，细棒分别对小球做功，所以每个小球的机械能不守恒. 说出“不同意”得3分，说出理由得2分 但对棒、小球组成的系统，机械能守恒：mgL+mg L 2=12m 2C v +12m 2B v （2分） 又v B =2vC , （1分）可解得： v C =15gL 5, v B =215gL5（2分） 17．质量不计的直角形支架两端分别连接质量为m 和2m 的小球A 和B 。

支架的两直角边长度分别为2l 和l ，支架可绕固定轴O 在竖直平面内无摩擦转动，如图所示。

开始时OA 边处于水平位置，由静止释放，则 （ ） A ．A 球的最大速度为gl )12(632- B ．A 球的速度最大时，两小球的总重力势能为零C ．A 球的速度最大时，两直角边与竖直方向的夹角为45°D ．A 、B 两球的最大速度之比v 1∶v 2=2∶116．质量不计的轻质弹性杆P 插在桌面上，杆端套有一个质量为m 的小球，今使小球沿水平方向做半径为R 的匀速圆周运动，角速度为ω，如图所示，则杆的上端受到的作用力大小为（C ）A. R m 2ωB. 24222R m g m ω-C.24222R m g m ω+D ．不能确定22．如图所示，轻杆长为3L ，在杆的A 、B 两端分别固定质量均为m 的球A 和球B ，杆上距球A 为L 处的点O 装在光滑的水平转动轴上，杆和球在竖直面内转动，已知球B 运动到最高点时，球B 对杆恰好无作用力．求：(1)球B 在最高点时，杆对水平轴的作用力大小．(2）球B 转到最低点时，球A 和球B 对杆的作用力分别是多大？方向如何？ 解：(1)球B 在最高点时速度为v 0，有Lvm mg 220=，得gL v 20=.此时球A 的速度为gL v 221210=，设此时杆对球A 的作用力为F A ，则 ,5.1,)2/(20mg F Lv mmg F A A ==-, A 球对杆的作用力为,5.1mg F A ='.水平轴对杆的作用力与A 球对杆的作用力平衡，再据牛顿第三定律知，杆对水平轴的作用力大小为F 0=1. 5 mg.(2)设球B 在最低点时的速度为B v ，取O 点为参考平面，据机械能守恒定律有222020)2(21212)2(21212B B v m m g L m v L m g v m m gL m v L m g +++⋅-=+-+⋅解得gL v B 526=。

动能势能机械能
动能是指物体因运动而具有的能量，它与物体的质量和速度有关。

动能的公式为：Ek = 1/2mv，其中Ek表示动能，m表示物体的质量，v表示物体的速度。

势能是指物体在某种力场中由于位置的不同而具有的能量，常见的有重力势能和弹性势能。

重力势能是指物体在重力场中的能量，它与物体的质量、重力加速度以及高度有关。

重力势能的公式为：Ep = mgh，其中Ep表示重力势能，m表示物体的质量，g表示重力加速度，h表示物体的高度。

机械能是指物体在力学运动中所具有的总能量，它等于动能和势能之和。

机械能的公式为：Em = Ek + Ep。

在物理学中，能量守恒定律指出，在一个封闭系统内，能量总量是不变的，即能量既不能被创造也不能被摧毁，只能转化为其他形式。

因此，在一个机械系统中，机械能的总量也是守恒的，即机械能不会因内部力发生改变而减少或增加。

动能、势能和机械能的概念及其相互转化是物理学中的基础，对于解析机械系统的运动状态和能量变化具有重要的意义。

- 1 -。

什么是势能有哪些不同类型的势能知识点：势能及其不同类型势能是指物体由于其位置或状态而具有的能量，它可以转化为其他形式的能量，如动能。

势能的大小取决于物体的质量、位置以及与其他物体的相互作用。

以下是势能的不同类型：1.重力势能：物体由于其位置在重力场中而具有的能量。

重力势能的大小取决于物体的质量、重力加速度以及物体相对于参考点的高度。

重力势能可以转化为动能，如物体从高处落下时。

2.弹性势能：物体由于其形变而具有的能量。

当物体被拉伸或压缩时，它存储了能量，这种能量称为弹性势能。

弹性势能可以转化为动能，如弹簧枪发射弹丸时。

3.电势能：带电物体由于其位置在电场中而具有的能量。

电势能的大小取决于物体的电荷、电场强度以及物体相对于参考点的电位。

电势能可以转化为动能，如带电粒子在电场中加速时。

4.磁势能：物体由于其位置在磁场中而具有的能量。

磁势能的大小取决于物体的磁矩、磁场强度以及物体相对于参考点的磁位。

磁势能可以转化为动能，如磁铁在磁场中受到力时。

5.分子势能：物体内部由于分子间的相互作用而具有的能量。

分子势能的大小取决于分子的质量、分子间距离以及分子间的相互作用力。

分子势能可以转化为动能，如物体受热时分子运动加剧。

以上是势能的一些基本类型，它们在不同领域和情境中具有重要的应用。

了解势能及其不同类型有助于我们更好地理解自然界中的能量转化和守恒定律。

习题及方法：1.习题：一个质量为2kg的物体从地面上方10m的地方自由落下，求物体落地前的重力势能。

重力势能的计算公式为：PE = mgh其中，m为物体的质量，g为重力加速度（约为9.8m/s²），h为物体的高度。

代入已知数值：g = 9.8m/s²PE = 2kg * 9.8m/s² * 10mPE = 196J答案：物体落地前的重力势能为196焦耳。

2.习题：一个弹簧被拉伸了0.1m，弹簧的劲度系数为100N/m，求弹簧储存的弹性势能。

物理动能与势能公式整理物理学中，动能和势能是两个重要的概念。

它们描述了物体在运动过程中的状态和性质。

本文将对动能和势能的公式进行整理和介绍，帮助读者更好地理解和应用这些公式。

一、动能公式动能是描述物体运动状态的物理量，用字母K表示。

动能与物体的质量和速度有关，其计算公式为：K = 1/2 * m * v²其中，K代表动能，m代表物体的质量，v代表物体的速度。

动能公式的推导过程如下：首先，我们可以将物体的速度v表示为位移s与时间t的比值：v = s/t。

其次，物体的位移s可以表示为速度v与时间t的乘积：s = v * t。

将上述两个等式代入动能公式中，得到：K = 1/2 * m * (s/t)²化简可得：K = 1/2 * m * (v * t)² / t²进一步简化为：K = 1/2 * m * v²动能的单位是焦耳（J），常用于描述物体的能量。

二、势能公式势能是描述物体位置状态的物理量，用字母U表示。

势能与物体的位置和力量有关，其计算公式根据具体情况而定。

下面将介绍两种常见的势能公式。

1. 重力势能重力势能是指物体在重力作用下的势能，计算公式为：Ug = m * g * h其中，Ug代表重力势能，m代表物体的质量，g代表重力加速度，h代表物体的高度。

重力势能的推导过程如下：物体的重力是其质量m与重力加速度g的乘积：Fg = m * g。

物体在高度h上所受的力为Fg，其位移为h。

根据力学功的计算公式W = F * s，重力势能可表示为：Ug = W= F * s= m * g * h2. 弹性势能弹性势能是指物体在弹性力作用下的势能，计算公式为：Us = 1/2 * k * x²其中，Us代表弹性势能，k代表弹簧的劲度系数，x代表弹簧的伸长或压缩距离。

弹性势能的推导过程如下：弹性力与弹簧的伸长或压缩距离成正比，即F = k * x。

根据力学功的计算公式W = F * s，弹性势能可表示为：Us = W= F * s= k * x * x= 1/2 * k * x²弹性势能的单位也是焦耳（J），常用于描述弹簧和弹性体的弹性性质。

势能与力的关系式
1、势能计算公式有重力势能，重力势能是物体因为重力作用而
拥有的能量，公式为EP=mgh，g应取9。

2、8N/kg。

3、m 质量，g应取弹性势能是物体因为弹性形变而具有的能量。

4、公式为EP=1/2 kx^2/kg，h物体据水平面的高度d(Ep)/dh=F。

5、也可写Ep=∫Fdh。

6、在相互作用力是“耗散力”（如摩擦力）时，设物体由A点（假设它是势能零点）移到B点克服它做功为W，当物体由B点回到A点时，它并不能对物体做功，故不能说由于耗散力存在使物体具有了势能。

7、与此相反，如果上述过程是在保守力作用下进行的，那么物体从B回到A时，保守力对物体做的功正好等于W，这是因为保守力所做的功才只与物体的初始和最终的相对位置有关。

8、如果物体不受其它力的作用那么这个功W就使物体得到同样多的动能。

9、故我们说物体在B点有势能W。

10、总之势能的大小由体系内各物体之间保守力所作的功来量度。

11、势能是属于物体系共有的能量，通常说一个物体的势能，实际上是一种简略的说法。

第十章机械能、内能及其转化一、机械能知识点梳理（一）、能1.物体能对外做功，我们就说这个物体具有能。

2.物体能够做的功越多，它具有的能就越大。

3.所有能量（功、能、热量）的单位都是焦耳。

（二）、动能：1.物体由于运动具有的能叫做动能。

Ek=1/2 mv2流动的空气、抛出的保龄球、飞行的子弹、行驶的汽车、跑步的运动员2.质量相同的物体，运动的速度越大，它具有的动能就越大；3.运动速度相同的物体，它的质量越大，它具有的动能就越大。

4.物体的动能与物体的质量和速度有关。

物体的质量越大，速度越大，它具有的动能就越多。

5.在探究动能大小与什么因素有关的实验中，用到了控制变量法和转换法。

（三）、重力势能：1.受到重力的物体被举高后也具有能，这种能叫作重力势能。

Ep=Gh=mgh。

高处的砖块、高处的江水、高处的重锤、高处的铁块、瀑布、流星2.质量相同的物体，高度越高，它具有的重力势能就越大；3.高度相同的物体，质量越大，它具有的重力势能就越大；4.物体的重力势能与物体的质量和高度有关。

物体质量越大，位置越高，它做功的本领就越大，物体具有的重力势能就越多。

5.在探究重力势能大小与什么因素有关的实验中，用到了控制变量法和转换法。

（四）、弹性势能：1.具有弹性的物体发生弹性形变后也具有能，这种能叫做弹性势能。

拉弯的弓、蹦床、皮筋、弹簧、篮球、撑杆、跳板2.同一弹性物体弹性形变越大，具有的弹性势能就越大。

（五）、机械能1.动能和势能〔重力势能、弹性势能〕统称为机械能。

(机械能E=动能Ek+势能Ep)。

2.物体动能和重力势能〔及弹性势能〕之间是可以发生互相转化的（六）、机械能守恒定律1.内容：物体动能和重力势能〔及弹性势能〕之间是可以发生互相转化的。

在只有动能和势能相互转化的过程中，机械能的总量保持不变，即机械能是守恒的。

2.物体初态的总机械能等于末态的总机械能。

3.物体减少的总重力势能等于物体增加的总动能。

（七）、功能关系1.当只有重力〔或弹簧弹力〕做功时，物体的机械能守恒。

动能与势能知识点总结动能和势能是物理学中的重要概念，它们描述了物体在运动过程中所具有的能量转化和储存情况。

本文将对动能和势能的基本概念、公式及应用进行总结和归纳。

一、动能的概念及公式动能是指物体由于运动而具有的能量。

当物体在空间中做运动时，会随着速度的增加而具有更多的动能。

动能的大小与物体的质量和速度的平方成正比，可以用下式来表达：动能（E_k）= 1/2 ×质量（m） ×速度的平方（v²）二、势能的概念及公式势能是指物体由于位置而具有的能量。

当物体处于某一位置时，具有相应的势能。

势能的大小取决于物体的位置以及与其他物体之间相互作用的情况。

常见的势能形式有重力势能、弹性势能和化学势能等。

1. 重力势能重力势能是指物体由于被抬高而具有的能量，可以用下式来计算：重力势能（E_p）= 质量（m） ×重力加速度（g） ×高度（h）2. 弹性势能弹性势能是指物体由于被压缩或拉伸而具有的能量，主要出现在弹簧和弹性体上。

弹性势能可以用下式来计算：弹性势能（E_p）= 1/2 ×弹性系数（k） ×形变的平方（x²）3. 化学势能化学势能是指物质之间由于反应而储存的能量。

例如，化学反应产生的化学键能就是一种化学势能。

化学势能的计算较为复杂，通常需要具体问题具体分析。

三、动能与势能的转化与守恒在物体运动或相互作用的过程中，动能和势能之间可以相互转化，且它们的总和保持不变。

具体转化方式如下：1. 动能转化为势能：当物体从高处下落时，动能会逐渐转化为重力势能。

例如，抛掷物体上升到最高点时，动能转化为重力势能，并随着下落过程中重力势能转化回动能。

2. 势能转化为动能：当物体从高处下落时，重力势能会转化为动能。

例如，高处物体自由下落时，重力势能逐渐减少，而动能逐渐增加。

3. 动能与势能的守恒：在物理系统中，动能与势能的总和是守恒的。

也就是说，当没有外力和能量损失时，动能与势能的总和保持不变。

重力势能、弹性势能、动能一、重力势能1定义：物体由于被举高而具有的能，叫做重力势能。

2公式：mgh E P =h ——物体具参考面的竖直高度3参考面a 重力势能为零的平面称为参考面；b 选取：原则是任意选取，但通常以地面为参考面若参考面未定，重力势能无意义，不能说重力势能大小如何选取不同的参考面，物体具有的重力势能不同，但重力势能改变与参考面的选取无关。

4标量，但有正负。

重力势能为正，表示物体在参考面的上方；重力势能为负，表示物体在参考面的下方；重力势能为零，表示物体在参考面上。

5单位：焦耳（J ）6重力做功特点：物体运动时，重力对它做的功只跟它的初、末位置有关，而跟物体运动的路径无关。

7、重力做功与重力势能变化的关系 p E W ∆-=（1）物体的高度下降时，重力做正功，重力势能减少，重力势能减少的量等于重力所做的功；（2）物体的高度增加时，重力做负功，重力势能增加，重力势能增加的量等于物体克服重力所做的功。

（3）重力势能变化只与重力做功有关，与其他力做功无关。

二、弹性势能1概念：发生弹性形变的物体的各部分之间，由于弹力的相互作用具有势能，称之为弹性势能。

2 弹力做功与弹性势能的关系 p E W ∆-=当弹簧弹力做正功时，弹簧的弹性势能减小，弹性势能变成其它形式的能；、当弹簧的弹力做负功时，弹簧的弹性势能增大，其它形式的能转化为弹簧的弹性势能。

这一点与重力做功跟重力势能变化的关系相似。

3势能：相互作用的物体凭借其位置而具有的能量叫势能，势能是系统所共有的。

三、动能1概念：物体由于运动而具有的能量，称为动能。

2动能表达式：221υm E K = 3动能定理（即合外力做功与动能关系）：12K K E E W -=4理解：①合F 在一个过程中对物体做的功，等于物体在这个过程中动能的变化。

②合F 做正功时，物体动能增加；合F 做负功时，物体动能减少。

③动能定理揭示了合外力的功与动能变化的关系。

4适用范围：适用于恒力、变力做功；适用于直线运动，也适用于曲线运动。

第四节重力势能1.重力做的功(1)表达式W G＝mgh＝mg(h1－h2)，其中h表示物体起点和终点的高度差，h1、h2分别表示物体起点和终点的高度。

(2)正负物体下降时重力做正功；物体被举高时重力做负功，也可以说成物体克服重力做功。

(3)特点物体运动时，重力对它做的功只跟它的起点和终点的位置有关，而跟物体运动的路径无关。

2．重力势能(1)定义：物体由于位于高处而具有的能量。

(2)大小：等于物体所受重力与所处高度的乘积，表达式为E p＝mgh，其中h 表示物体所在位置的高度。

(3)单位：焦耳，与功的单位相同。

重力势能是标量，正负表示大小。

(4)重力做功与重力势能变化的关系①表达式：W G＝E p1－E p2。

②重力做正功，重力势能减小；重力做负功，重力势能增大。

3．重力势能的相对性和系统性(1)相对性①参考平面：物体的重力势能总是相对于某一水平面来说的，这个水平面叫做参考平面，在参考平面，物体的重力势能取作0。

②重力势能的相对性选择不同的参考平面，物体重力势能的数值是不同的。

对选定的参考平面，上方物体的重力势能是正值，下方物体的重力势能是负值，负值的重力势能，表示物体在这个位置具有的重力势能要比在参考平面上具有的重力势能小。

(2)系统性重力势能是地球与物体所组成的系统共有的。

判一判(1)重力势能E p1＝2 J，E p2＝－3 J，则E p1与E p2方向相反。

()(2)同一物体的重力势能E p1＝2 J，E p2＝－3 J，则E p1>E p2。

()(3)在同一高度的质量不同的两个物体，它们的重力势能一定不同。

()提示：(1)×重力势能是标量，没有方向。

(2)√重力势能为正值，表示物体处于参考平面的上方，为负值表示物体处于参考平面的下方，而同一物体在越高的地方重力势能越大。

(3)×若选定两物体所处的水平面为参考平面，则两物体的重力势能均为0。

说明：(1)重力做功与路径无关，只与始末位置的高度差有关。