几种常见的曲面及其方程.

各种曲面的方程
1. 球面方程
球面是一种非常常见的曲面，它的方程为：
(x-a)² + (y-b)² + (z-c)² = r²
其中，a、b、c分别为球心的坐标，r为球的半径。

这个方程描述了一个以(a,b,c)为球心，半径为r的球面。

球面在几何学中有着广泛的应用，比如在计算机图形学中，球面可以用来表示三维空间中的物体表面，比如球体、球形天体等等。

2. 椭球面方程
椭球面是一种比球面更加复杂的曲面，它的方程为：
(x/a)² + (y/b)² + (z/c)² = 1
其中，a、b、c分别为椭球面在x、y、z轴上的半轴长度。

这个方程描述了一个以原点为中心，半轴长度分别为a、b、c的椭球面。

椭球面在几何学中也有着广泛的应用，比如在地球科学中，椭球面可以用来表示地球的形状，以及计算地球的重力场等等。

3. 双曲面方程
双曲面是一种非常特殊的曲面，它的方程为：
(x/a)² + (y/b)² - (z/c)² = 1
其中，a、b、c分别为双曲面在x、y、z轴上的半轴长度。

这个方程描述了一个以原点为中心，半轴长度分别为a、b、c的双曲面。

双曲面在几何学中也有着广泛的应用，比如在物理学中，双曲面可以用来表示电磁场中的等势面，以及计算电场、磁场等等。

曲面方程是几何学中非常重要的一部分，它们可以用来描述各种不同形状的曲面，以及在各种不同领域中的应用。

常用曲线和曲面的方程及其性质曲线和曲面在三维空间中是常见的数学对象。

它们的方程可以通过几何性质描述它们的性质。

本文将介绍一些常用的曲线和曲面方程及其性质。

一、曲线方程1. 直线方程直线是一种最基本的曲线，它的方程可以写成一般式和斜截式两种形式。

一般式：$Ax+By+C=0$；斜截式：$y=kx+b$，其中$k$是直线的斜率，$b$是截距。

直线的斜率表示的是直线倾斜的程度，斜率越大表示直线越陡峭。

斜率等于零表示直线水平，而无限大则表示直线垂直于$x$轴。

2. 圆的方程圆是一种具有球面对称性质的曲线，它的方程可以写成两种形式：标准式和一般式。

标准式：$(x-a)^2+(y-b)^2=r^2$，其中$(a,b)$为圆心坐标，$r$为半径长度。

一般式：$x^2+y^2+Ax+By+C=0$，其中$A,B,C$是常数。

圆的标准式方程可以通过圆心和半径来描述圆的几何性质；而一般式方程则可以通过求圆的中心和半径来转化为标准式方程。

3. 椭圆的方程椭圆是一种内离于两个焦点的平面曲线，它的方程可以写成一般式和标准式两种形式。

标准式：$\frac{(x-a)^2}{a^2}+\frac{(y-b)^2}{b^2}=1$，其中$(a,b)$为椭圆中心坐标，$a$是横轴半径，$b$是纵轴半径。

一般式：$Ax^2+By^2+Cx+Dy+E=0$，其中$A,B,C,D,E$是常数。

椭圆的标准式方程中的$a$和$b$决定了椭圆的形状和大小。

当$a=b$时，椭圆变成了圆。

4. 抛物线的方程抛物线是一种开口朝上或朝下的U形曲线，它的方程可以写成两种形式：标准式和一般式。

标准式：$y=ax^2$，其中$a$是抛物线的参数。

一般式：$Ax^2+By+C=0$，其中$A,B,C$是常数。

抛物线的标准式方程中的参数$a$可以决定抛物线的开口方向，当$a>0$时开口向上，$a<0$时则开口向下。

5. 双曲线的方程双曲线是一种形状类似于抛物线的曲线，但它却有两个分支。

常见曲面方程总结(一)前言•引言：曲面是数学中的重要概念，广泛应用于计算机图形学、工程设计等领域。

在形状设计和模拟中，掌握常见曲面方程是非常重要的基础知识。

本文将介绍几种常见的曲面方程，并分析其特性和应用场景。

正文一、球面方程•定义：球面是由到定点距离相等于固定半径的点所组成的曲面。

它的方程一般可以表示为：(x-a)² + (y-b)² + (z-c)² = r²，其中(a,b,c)为球心坐标，r为半径。

•特性：球面是空间中对称性最高的曲面，具有旋转对称性、轴对称性和平面对称性。

•应用：球面方程广泛应用于计算机图形学中的三维建模，如球体、球形光源等。

二、圆柱面方程•定义：圆柱面是围绕某条直线旋转而形成的曲面。

它的方程可以表示为：(x-a)² + (y-b)² = r²，其中(a,b)为圆心坐标，r为半径。

•特性：圆柱面在与旋转轴垂直的方向上是无限延伸的，而在旋转轴方向上是有限长度的。

•应用：圆柱面方程常用于描述圆柱体、柱形物体等实际物体的几何特征。

三、锥面方程•定义：锥面是由定点到平面上所有点的连线所组成的曲面。

它的方程可以表示为：(x-a)² + (y-b)² = z²，其中(a,b)为锥顶坐标。

•特性：锥面在平面上形成对称的圆锥形状，而在垂直于平面的方向上是无限延伸的。

•应用：锥面方程常用于描述圆锥体、棱锥体等实际物体的几何特征。

四、椭球面方程•定义：椭球面是由到两个定点的距离之和等于常数的点所组成的曲面。

它的方程可以表示为：(x-a)²/r₁² + (y-b)²/r₂² + (z-c)²/r₃² = 1，其中(a,b,c)为椭球中心坐标，r₁、r₂、r₃为轴长。

•特性：椭球面可以是旋转椭球、扁椭球或球体等不同形状，取决于轴长的比值。

一、二次曲面
1-1球面
(X-X0)2+(Y-Y0)2+(Z-Z0)2=R2
球心为M0(X0,Y0,Z0)
1-2椭圆锥面
1-3椭球面
其中，表示xOz平面上的椭圆绕z轴旋转而成的椭球面。

1-4单叶双曲面
其中，表示xOz平面上的双曲线绕z轴旋转而成的单叶双曲面。

1-5双叶双曲面
其中，表示xOz平面上的双曲线绕x轴旋转而成的双叶双曲面。

1-6椭圆抛物面
1-7双曲抛物面（马鞍面）
二、柱面
2-1圆柱面
X2+Y2=R2
2-2椭圆柱面
2-3双曲柱面
2-4抛物柱面
y2=2px
注：形如二、柱面只含x,y而缺少z的方程F(x,y)=0在空间直角坐标系中表示母线平行于z 轴的柱面，其准线为xOy平面上的曲线C：F(x,y)=0
特别地，
1.球x2+y2+z2=R2
2.圆柱面x2+y2=R2
3.旋转抛物面X2+Y2=z(以原点为顶点，上下两个开口分别向上向下的抛物线旋转而成的图形)
4.X2+Y2=z2(以原点为顶点，上下两个开口分别向上向下的圆锥，锥顶角为90。

)。

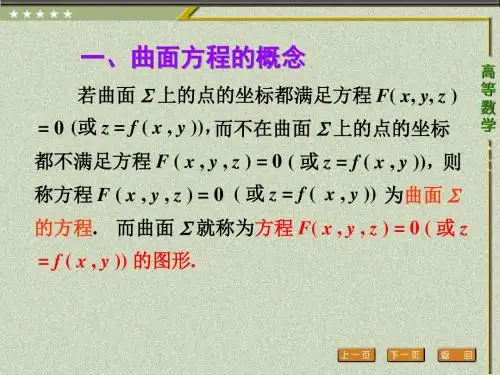
江西理工大学理学院第 4 节曲面、空间曲线及其方程江西理工大学理学院一、曲面方程的概念曲面的实例： 水桶的表面、台灯的罩子面等． 曲面在空间解析几何中被看成是点的几何轨迹． 曲面方程的定义：如果曲面 S 与三元方程 F ( x , y , z ) = 0 有下述关系：（1）曲面 S 上任一点的坐标都满足方程； （2）不在曲面 S 上的点的坐标都不满足方程；那么，方程 F ( x , y , z ) = 0 就叫做曲面 S 的方程， 而曲面 S 就叫做方程的图形．江西理工大学理学院以下给出几例常见的曲面.例 1 建立球心在点 M 0 ( x 0 , y0 , z 0 ) 、半径为 R 的球面方程.解设 M ( x , y , z ) 是球面上任一点，根据题意有| MM 0 |= R2 22 2 2( x − x0 )2+ ( y − y0 ) + ( z − z 0 ) = R2所求方程为 ( x − x0 ) + ( y − y0 ) + ( z − z0 ) = R 特殊地：球心在原点时方程为 x + y + z = R2 2 22江西理工大学理学院例 2 求与原点O 及 M 0 ( 2,3,4)的距离之比为1 : 2 的 点的全体所组成的曲面方程.解设 M ( x , y , z ) 是曲面上任一点，| MO | 1 = , 根据题意有 | MM 0 | 2 x2 + y2 + z2( x − 2) + ( y − 3) + (z − 4)2 221 = , 222⎞ 4 ⎞ 116 2 ⎛ ⎛ . 所求方程为 ⎜ x + ⎟ + ( y + 1) + ⎜ z + ⎟ = 3⎠ 3⎠ 9 ⎝ ⎝2江西理工大学理学院例 3 已知 A(1,2,3) ， B( 2,−1,4)，求线段 AB 的 垂直平分面的方程.解设 M ( x , y , z ) 是所求平面上任一点，根据题意有 | MA |=| MB |,( x − 1) + ( y − 2 ) + ( z − 3 )2 22( x − 2)2 + ( y + 1)2 + ( z − 4)2 , =化简得所求方程 2 x − 6 y + 2 z − 7 = 0.江西理工大学理学院2 2 例4 方程 z = ( x − 1) + ( y − 2) − 1的图形是怎样的？解根据题意有 z ≥ −1用平面 z = c 去截图形得圆：z( x − 1)2 + ( y − 2) 2 = 1 + c (c ≥ −1)当平面 z = c 上下移动时， 得到一系列圆coxy圆心在(1,2, c )，半径为 1 + c半径随c 的增大而增大. 图形上不封顶，下封底．江西理工大学理学院以上几例表明研究空间曲面有两个基本问题： （1）已知曲面作为点的轨迹时，求曲面方程． （讨论旋转曲面） （2）已知坐标间的关系式，研究曲面形状． （讨论柱面、二次曲面）江西理工大学理学院二、旋转曲面定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴．播放 播放江西理工大学理学院旋转过程中的特征： 如图设 M ( x , y , z ),z⋅ M ( 0, y , z ) ⋅ Md1 1 1(1) z = z1（2）点 M 到 z 轴的距离o x2 2f ( y, z ) = 0yd=x + y =| y1 |2 2将 z = z1 , y1 = ± x + y 代入f ( y1 , z1 ) = 0江西理工大学理学院z = z1 , y1 = ± x 2 + y 2 代入 f ( y1 , z1 ) = 0 将得方程f (± x + y , z = 0,2 2)yoz 坐标面上的已知曲线 f ( y , z ) = 0 绕 z 轴旋转一周的旋转曲面方程.同理： yoz 坐标面上的已知曲线 f ( y , z ) = 0 绕 y 轴旋转一周的旋转曲面方程为f y, ±(x 2 + z 2 = 0.)江西理工大学理学院例 5 直线 L绕另一条与 L相交的直线旋转一周， 所得旋转曲面叫圆锥面．两直线的交点叫圆锥面 ⎛ 0 < α < π ⎞ 叫圆锥面的 的顶点，两直线的夹角 α ⎜ ⎟ 2⎠ ⎝ 半顶角．试建立顶点在坐标原点，旋转轴为 z 轴， 半顶角为α 的圆锥面方程． z解yoz 面上直线方程为 z = y cot α2 2⋅ αoM 1 (0, y1 , z1 )y圆锥面方程z = ± x + y cot αxM ( x , y, z )江西理工大学理学院例6 将下列各曲线绕对应的轴旋转一周，求 生成的旋转曲面的方程．⎧ x2 z2 ⎪ 2 − 2 =1 （1）双曲线 ⎨ a 分别绕 x 轴和 z 轴； c ⎪ y=0 ⎩x2 y2 + z2 绕 x 轴旋转 − =1 2 2 a c x +y z − 2 =1 绕 z 轴旋转 2 a c2 2 2旋 转 双 曲 面⎧ y2 z2 ⎪ 2 + 2 =1 （2）椭圆 ⎨ a 绕 y 轴和 z 轴； c ⎪x = 0 ⎩ y2 x2 + z2 旋 绕 y 轴旋转 + =1 2 2a c x +y z + 2 =1 绕 z 轴旋转 2 a c2 2 2江西理工大学理学院转 椭 球 面⎧ y 2 = 2 pz （3）抛物线 ⎨ 绕 z 轴； ⎩x = 0x 2 + y 2 = 2 pz旋转抛物面江西理工大学理学院三、柱面定义 平行于定直线并沿定曲线 C 移动的直线 L 所形成的曲面称为柱面. 这条定曲线 C 叫柱面的准线 ，动直线 L 叫 柱面的母线. 观察柱面的形 成过程:播放 播放江西理工大学理学院柱面举例zzy = 2x2平面o xo xyyy= x抛物柱面江西理工大学理学院从柱面方程看柱面的特征：只含 x, y 而缺 z 的方程 F ( x , y ) = 0 ，在 空间直角坐标系中表示母线平行于 z 轴的柱 面，其准线为 xoy 面上曲线C . （其他类推）实 例y z + 2 = 1 椭圆柱面 // x 轴 2 b c x2 y2 − 2 = 1 双曲柱面 // z 轴 2 a b 2 抛物柱面 // y 轴 x = 2 pz22江西理工大学理学院四、空间曲线的一般方程空间曲线C可看作空间两曲面的交线.⎧F ( x, y, z ) = 0 ⎨ ⎩G ( x , y , z ) = 0空间曲线的一般方程 特点：曲线上的点都满足 方程，满足方程的点都在 曲线上，不在曲线上的点 不能同时满足两个方程.zS1 S2oxCy江西理工大学理学院⎧ x2 + y2 = 1 例7 方程组 ⎨ 表示怎样的曲线？ ⎩2 x + 3 y + 3z = 6解x 2 + y 2 = 1 表示圆柱面，2 x + 3 y + 3 z = 6 表示平面，⎧ x2 + y2 = 1 ⎨ ⎩2 x + 3 y + 3z = 6交线为椭圆.江西理工大学理学院⎧z = a2 − x2 − y2 ⎪ 2 表示怎样的曲线？ 例8 方程组 ⎨ a 2 a 2 ⎪( x − ) + y = ⎩ 2 4解z = a2 − x2 − y2上半球面,a 2 a2 2 圆柱面, (x − ) + y = 2 4交线如图.江西理工大学理学院五、空间曲线的参数方程⎧ x = x(t ) ⎪ ⎨ y = y( t ) 空间曲线的参数方程 ⎪ z = z( t ) ⎩当给定 t = t1 时，就 得到曲线上的一个点( x1 , y1 , z1 )，随着参数的变化可得到曲线上的全部点.,0αb +空间曲线投影柱面。