Voronoi图矢量算法

路径规划的主要算法与展望-应用数学论文-数学论文——文章均为WORD文档，下载后可直接编辑使用亦可打印——摘要：路径规划算法是智能领域中一项新兴的关键支撑技术；依据路径规划算法的实现原理，将其分为进化型算法与非进化型算法；再依据数学特征将非进化型算法细分为经典数学与几何图论两类；针对每类算法，分别从发展背景、设计思想、优缺点、改进与发展等方面简要归纳分析；最后对路径规划算法的未来发展趋势进行展望。

关键词：路径规划; 进化型算法; 非进化型算法; 未来展望;Summary of Path Planning AlgorithmsLIANG Xiao-hui MU Yong-hui WU Bei-hua JIANG YuShijiazhuang Campus of Army Engineering UniversityAbstract：Path planning algorithm is an emerging key supporting technology in the field of intelligence; According to the implementation principle of path planning algorithm, it is divided into evolutionary algorithm and non-evolutionary algorithm; Then based on the mathematical characteristics, the non-evolutionary algorithm can be divided into two types: classical mathematics and geometric graph theory; For each type of algorithm, the paper will give a brief summary and analysis from some aspects: the background of development,design ideas, advantages and disadvantages, improvement. Finally the future development trend of the path planning algorithm is forecasted.0 引言路径规划（Path Planning)[1]是智能技术中的热点研究问题，已在多领域有所突破并成功得以应用。

编写容易 分治法构造Delaunay三角剖分法 易于理解
Voronoi图的构造
用分治法构造角最优三角剖分，首先要对点集依照X坐 标排序。如果点集内点的个数小于等于三，那么可以直接构 造，否则将点集拆分成为两个含点数目近似的点集进行构造， 最后合并这两个点集。
点集内含点 个数为2的
情况
点集内含点 个数为3的
新增点
Voronoi图拓宽解题思路 原来障碍点
接下来，由于人还可以从走廊边与障碍物之间通过，那么对于每一个障 碍点(x,y)我们可以在走廊壁上增加障碍点(x,0),(x,W),一共增加2n个障碍 点 。 另外 在走 廊开 始和尽 头增 加四个 障碍 点（ -W,0），（-W,W）， （L+W,0），（L+W,W）这四个点与其它点之间距离不小与W，这样就 不影响结果。然后对于这3n+4个点求Voronoi图。
Ta
c
a
Tb b
Voronoi图与平面MST问题
根据这个条件，我们可以得到一个新的方案，构造角 最优三角剖分，然后计算最小生成树，总的时间复杂度是 O(n log n)。
可能大家会问这样一个问题：
除了距离问题,Voronoi图还有什么用呢?
我想告诉大家！Voronoi图不仅能快速解决距离问题
Voronoi图还可以扩宽我们的解题思路
的
交
点
D C
B
所求点
A
Voronoi图的在信息学中的应用
根据刚才分析的两种情况，我们可以构造两种方 案。第一种方案针对所求点为过三个点的圆的圆心的 状态，我们枚举三个点，求出它们组成的三角形的外 心和半径，然后枚举其它的点，看它们是不是在这个 圆中。第二种方案是枚举两个点的中垂线，求出中垂 线与矩形的交点，然后根据这三个点来计算最远位置， 进行判断。

( si s ) n s
湖北大学资源环境学院
i 1
王新生 2019/3/9
点集分布的判别标准
当某个点集的空间分布为规则分布时，CV是 低的。当为集群分布时，在集群（“类”）内的 Voronoi多边形面积较小，而在集群间的面积较大， CV是高的。但是，应该注意的是，规则的周期结 构也会导致较高的CV值；周期性重复出现的集群 分布也会形成高的CV值。 Duyckaerts and Godefroy （2000）提出了三 个建议值，当点集为随机分布时，CV值为57% （包括从33%到64%）；当点集为集群分布时， CV值为92%（包括大于64%）；当点集为规则分 布时，CV值为29%（包括小于33%）
湖北大学资源环境学院
的随机分布，不同于泊 松分布的两种情况是空间规则分布和集群分布。 Voronoi分割可以帮助我们判断点集的空间分布属 于那一种形式。当点集在平面上呈现泊松分布时， Voronoi多边形面积是有变化的，有些是面积大的 Voronoi多边形，有些是面积小的Voronoi多边形。 Voronoi多边形面积的变化性是很容易通过其方差来估 计的。变异系数（the coefficient of variation, CV）是 Voronoi多边形面积的标准差与平均值的比值，它可以 衡量现象在空间上的相对变化程度。 n 标准差计算公式： 2

湖北大学资源环境学院
王新生 2019/3/9
湖北大学资源环境学院
王新生 2019/3/9
任意形状发生元Voronoi图构建的栅格方法
1 d ( p ,p d ( p ,p w , w i) i) i 2 w i 1
wi1>0、wi2是加权Voronoi图的权重。 当 wi2=0 时 产 生 倍 增 的 加 权 Voronoi 图

目前矢量方法用离散点集代替线面，使空间实体的完整性 遭到破坏，同时生成的V图，要经过复杂的识别和修补工 作，这是一个尚待克服的困难；
增添法的基本步骤：
①搜索最邻近单元和相邻单元
最邻近单元为Pn+1所在原V图中某点 的Voronoi多边形Vk以及原来与它 相邻的若干个多边形及相应生成 元；
②局部更新
对于各邻近单元，首先与最邻近单
元Vk中Pk作中垂线，并找其余Vk 的交点，由于Vk是凸多边形，因 而只产生两个交点1、2，1与2连 线把与Vk相关的单元分为“两 半”：与Pn+1“相关的一半”及 “不相关的一半”，使Pn+1与相 关一半的各生成元Pk+1， Pk+2…作 中垂线围成各封闭多边形，即是
增添法 部件合成法
（一）对偶生成法
对偶生成法：主要是指生成V图时先生成其对偶元 Delaunay三角网，再通过做三角网每一三角形三条 边的中垂线，形成以每一三角形顶点为生成元的多 边形网 。
对偶生成法生成V图
对偶生成法的关键是Delaunay三角网的生成。
Delaunay三角网的特性： 任一三角形外接圆内部包含其他点； 三角形均衡或三边均衡，其最小角最大； 使三角网总边长最小； 在确定的n个点上，构造的Delaunay三角网网形唯一。
部件合成
（四）矢量方法生成V图的分析
以上三种方法是矢量方法中常用的，随着并行处理技术的 发展，V图生成页、也出现了并行算法，它使各生成元同 时进行各点的V图计算；
矢量方法生成V图的算法和数据结构都较为复杂，其生成 元是基于离散点集的，对于实际的地理信息，这远远不够， 应该拓展成点、线、面、体及其组合的复杂形体；
Vi Vj
PV1 V2 ...Vn R2 （假定到Pi为0的点不算在Vi内）

目前矢量方法用离散点集代替线面，使空间实体的完整性 遭到破坏，同时生成的V图，要经过复杂的识别和修补工 作，这是一个尚待克服的困难；
对于光滑、不光滑组合曲线及相应组合成的封闭面域，尽 管可用折线逼近，但折线毕竟不是曲线，在曲线光滑处， 每一点都是转折点，而化为折线，折线交接处的点就成为 唯一转折点，性质突变处。
义G的Voronoi图V（G）为
V（G）={V(g1)，V(g2)，…，V(gn)} 一般V图特性在广义V图中类似存在。
5.2 V图生成方法
V图有着按距离划分邻近区域的普遍特性，应 用范围广。
生成V图的方法很多，一般分为两种： 矢量方法 栅格方法
一、生成V图的矢量方法
矢量方法生成V图大多是对点实体。 方法分为：对偶生成法
义G的Voronoi图V（G）为
V（G）={V（g1），V（g2），…，V（gn）}
V图是与距离紧密相关的，而距离值是由尺度所 基本定义的。不同尺度，距离的概念不一样， 数值往往也不一样，因此不同的尺度空间，有 不同的V图。上述定义同样可推广到3维。
（二）广义Voronoi图
拓展Voronoi图为广义Voronoi图具有广泛意义。
（二）性质
假设平面上有n个离散点，其对应的Voronoi多边
形分别为V1，V2…Vn， Voronoi多边形之间除边
界外，其交集为空集，所有Voronoi多边形的并集 为二维平面R2，即
Vi Vj
PV1 V2 ...Vn R2 （假定到Pi为0的点不算在Vi内）
V1 V2 ...Vn R2
V图、障碍V图、广义V图的多边形边界提供了点、 线、面全形态，障碍、非障碍完备空间，广义加 权距离的等距线、等比线、等势线等，是具有严 密数学意义且极广泛使用价值的轨迹线。

维诺图（VoronoiDiagram）分析与实现一、问题描述1.Voronoi图的定义又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。

2.Voronoi图的特点（1）每个V多边形内有一个生成元；（2）每个V多边形内点到该生成元距离短于到其它生成元距离；（3）多边形边界上的点到生成此边界的生成元距离相等；（4）邻接图形的Voronoi多边形界线以原邻接界线作为子集。

3.Voronoi的应用在计算几何学科中的重要地位，由于其根据点集划分的区域到点的距离最近的特点，其在地理学、气象学、结晶学、航天、核物理学、机器人等领域具有广泛的应用。

如在障碍物点集中，规避障碍寻找最佳路径。

二、算法分析与设计Voronoi图有着按距离划分邻近区域的普遍特性，应用范围广。

生成V图的方法很多，常见的有分治法、扫描线算法和Delaunay三角剖分算法。

1.建立Voronoi图方法和步骤本次实验采用的是Delaunay三角剖分算法。

主要是指生成Voronoi图时先生成其对偶元Delaunay三角网，再找出三角网每一三角形的外接圆圆心，最后连接相邻三角形的外接圆圆心，形成以每一三角形顶点为生成元的多边形网。

如下图所示。

建立Voronoi图算法的关键是对离散数据点合理地连成三角网，即构建Delaunay三角网。

建立Voronoi图的步骤为：（1）离散点自动构建三角网，即构建Delaunay三角网。

对离散点和形成的三角形编号，记录每个三角形是由哪三个离散点构成的。

（2）计算每个三角形的外接圆圆心，并记录之。

（3）遍历三角形链表，寻找与当前三角形pTri三边共边的相邻三角形TriA，TriB和TriC。

（4）如果找到，则把寻找到的三角形的外心与pTri的外心连接，存入维诺边链表中。

如果找不到，则求出最外边的中垂线射线存入维诺边链表中。

（5）遍历结束，所有维诺边被找到，根据边画出维诺图。

Voronoi图定义任意两点p 和q 之间的欧氏距离，记作 dist(p, q) 。

就平面情况而言，我们有dist(p, q) = (px-qx)2+ (py-qy)2设P := {p1, …, pn}为平面上任意 n 个互异的点；这些点也就是基点。

按照我们的定义，所谓P对应的Voronoi图，就是平面的一个子区域划分——整个平面因此被划分为n 个单元（cell ），它们具有这样的性质：任一点q位于点pi 所对应的单元中，当且仅当对于任何的pj∈Pj, j≠i,都有dist(q, pi)<dist(q, pj)。

我们将与P对应的Voronoi图记作Vor(P)。

“Vor(P) ”或者“Voronoi图”所指示的仅仅只是组成该子区域划分的边和顶点。

在Vor(P)中，与基点pi 相对应的单元记作V (pi)——称作与pi 相对应的Voronoi单元（Voronoi cell）。

上图是Voronoi图，下图的蓝色点围成的区域（凸包）是它对应的Delaunay三角剖分。

任给平面上两点p 和q ，所谓 p 和q 的平分线（bisector），就是线段 pq 的垂直平分线。

该平分线将平面划分为两张半平面（half-plane）。

点 p 所在的那张开半平面记作 h(p, q) ，点 q 所在的那张开半平面记作 h(q, p) 。

请注意，r ∈ h(p, q) 当且仅当 dist(r, p) < dist(r, q) 。

据此，可以得出如下观察结论：V (pi) = ∩ h(pi, pj) , 1≤j≤n, j≠ i也就是说，V (pi)是(n-1)张半平面的公共交集；它也是一个（不见得有界的）开的凸多边形（convex polygon）子区域.很显然，Voronoi顶点到相邻的三个site距离相等；Voronoi边上任意一点到相邻的两个site距离相等；对于任何点q，我们将以q为中心、内部不含P中任何基点的最大圆，称作q关于P的最大空圆（largest empty circle ），记作Cp(q)。

加权 V or onoi 图是对 V o ronoi 图(即以 点为 生成 元 的普 通 V or onoi 图)的生成元赋以权 重值而 形成的 V or onoi 图[ 2] , 而分区加权 V or onoi 图是 对加权 Vo ro no i 图的扩 展 。 所谓分 区加权 V oro no i 图 , 就是将各生成元周围划 分为不同的 扇区 , 并给每个扇 区赋以自己 的权重值 , 由此 构造出来的 一种新的 Vo ro noi 图 , 这种 V or onoi 图可用于处理蜂窝制移动通信系统 中的基站优化问题 。 为便于 该应用 , 本文 还给出 了分区 加权 Vo ro noi 图生成 过 程中 形 成的 不 同 类型 区 域面 积 的 计算 方 法。
· 195 ·
图1
Vo ro noi 图的基本性质[ 4] 如下 。 性质 1 生成元 pi 的 V o ronoi 区域 V(pi)无界 的充分必 要条件是 pi ∈ BC H(P), 其中 BC H(P)表示生成 元集合 S 的 凸壳边界 。 性质 2 n 个点的 点集 S 的 Vo ro noi 图至多 有 2n -5 个 顶点和 3n -6 条边 。 性质 3 每个 Vo ro no i 点恰好是 3 条 Vo ro noi 边的交点 。 性质 4 点集 S 中的 点 p i 的 每一 个最 近临 近点 确定 V (pi)的一条边 。 2 .2 加权 V o ronoi 图 定义 2 给定平面 上 n 个点的 集合 S ={p1 , p2 , … , pn}, 对每个生成元 pi(i =1, 2 , … , n), 赋以非 负实数权重 vi(i =1 , 2 , … , n), 称 D(p , pi)=d(p -pi)/ vi 为 p 和 p i 间 的加 权距 离 , 称 V(pi , vi)=∩ {p D(p , pi)<D(p , pj)}为 点 pi 的权重

GIS原理与算法第七章Voronoi图构建算法（based on Raster）2011.6主要内容预备知识并行生长算法传统距离变换动态距离变换算法栅格算法实例球面V的生成算法原理球面格网算法实例问题讨论？？意义矢量算法对于点集十分有效，对于线集变得比较复杂，面状集则非常困难，推广到三维Voronoi图和球面Voronoi图的矢量算法则更为复杂。

算法的复杂性是Voronoi图在动态GIS模型中难以得到广泛应用的主要原因。

为解决这个矛盾，C.Gold & Yang[1992,1996]提出一个点线模型，即把复杂实体分解成点和直线，先构建点线的Voronoi图，再转换为实体的Voronoi 图。

意义•此方法的优点是结构简单，能直接建立实体的四边数据结构和容易处理区域实体的动态变化，•但是此方法缺乏数据的层次结构（即数据综合），难以从根本上解决海量数据的不同层次的综合表达。

扩展模板最简单的距离扩展模板是3×3的正方形模板，其距离扩张如图所示：扩展模板其他模版还有：菱形模版、棋盘模版、八边形模版等：只要上述a，b的取值满足1<b/a<2，那么它就是“欧氏距离”在平面栅格空间的一个整数近似。

(a) 菱形模版(b)棋盘模版(c)八边形模版不同的模板给出的栅格距离不同，如下图：对于这些距栅格VD定义栅格膨胀和腐蚀算子膨胀(dilation)和腐蚀(erosion)是数学形态学的两个基本算子。

A是原始影像，B是结构元。

定义如下：bBbbBbABAABA∈∈=Θ=⊕IU::腐蚀膨胀膨胀和腐蚀算子 膨胀和腐蚀原理：分解图（2）4、动态距离变换算法采用距离变换后，由于取整带来的误差，与欧氏距离之间的差异随距离的增大而增大，如下图：动态距离变换原理实验结果意义与研究现状由于现代测绘及相关技术的发展，人们研究的区域逐渐从局部区域发展到覆盖整个地球。

而地球本身就是一个近似的椭球体，研究球面Voronoi图的生成方法对于全球数据的动态管理和球面空间关系的推理有其重要的意义。

voronoi协方差法向量
Voronoi 协方差法向量是指在 Voronoi 图形的每个顶点处计算
的协方差矩阵的特征向量。

Voronoi 图形是指根据一组离散点将空
间分割成多个区域的图形。

在计算机图形学和计算机视觉中，Voronoi 协方差法向量通常用于表征三维模型表面的几何特征。

在计算 Voronoi 协方差法向量时，首先需要计算每个 Voronoi 区域的质心，然后以质心为中心计算协方差矩阵。

协方差矩阵是一
个对称矩阵，它描述了数据集中两个不同维度之间的线性关系。

对
协方差矩阵进行特征值分解，得到的特征向量即为 Voronoi 协方差
法向量。

Voronoi 协方差法向量在三维模型分割和特征提取中具有重要
作用。

通过计算每个 Voronoi 区域的协方差矩阵特征向量，可以获
得表面的法向量信息，这对于模型的分割和识别非常有帮助。

此外，Voronoi 协方差法向量也可以用于三维模型的压缩和简化，以及在
计算机辅助设计和计算机图形学中的应用。

总之，Voronoi 协方差法向量是一种用于表征三维模型表面几
何特征的方法，通过计算 Voronoi 区域的协方差矩阵特征向量，可
以得到模型表面的法向量信息，对于模型分割、特征提取和压缩具有重要意义。

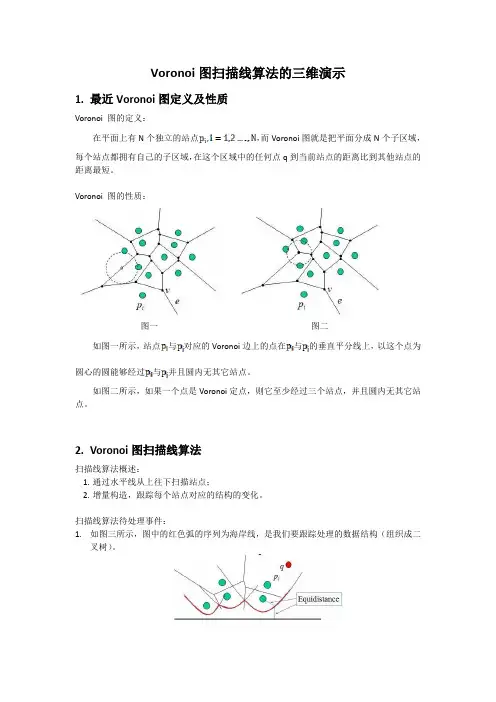
Voronoi图扫描线算法的三维演示1.最近Voronoi图定义及性质Voronoi 图的定义：在平面上有N个独立的站点，而Voronoi图就是把平面分成N个子区域，每个站点都拥有自己的子区域，在这个区域中的任何点q到当前站点的距离比到其他站点的距离最短。

Voronoi 图的性质：图一图二如图一所示，站点与对应的Voronoi边上的点在与的垂直平分线上，以这个点为圆心的圆能够经过与并且圆内无其它站点。

如图二所示，如果一个点是Voronoi定点，则它至少经过三个站点，并且圆内无其它站点。

2.Voronoi图扫描线算法扫描线算法概述：1.通过水平线从上往下扫描站点；2.增量构造，跟踪每个站点对应的结构的变化。

扫描线算法待处理事件：1.如图三所示，图中的红色弧的序列为海岸线，是我们要跟踪处理的数据结构（组织成二叉树）。

图三2.图四中到两个站点及扫描线相等的点为分裂点，为海岸线结构中的重要成分，实际上为二叉树中的内点，而每条弧则为叶子节点。

图四3.图五和图六为两个连续的瞬间，图五中间的那条弧即将消失，取而代之的是Voronoi顶点。

它的两条边为分裂点生长而成。

图五图六我们所用的数据结构：1.用DCEL记录Voronoi图：图七Vertex：点的辅助信息bool inner; 表示该点是不是一个内部点（非边界点）vector<int> inTris; 记录该点所在的三角形号vector<int> inTrisOrd; 记录该点在相应三角形中的编号（只取0，1，2）int startHe; 该点起始半边编号int endHe; 该点终止半边编号（仅对边界点有效）HalfFace3：面辅助信息int he[3]; 记录一个面中三条半边号码HalfEdge：基础半边结构int fv; 起始点int tv; 终止点int fn; 面号int prev; 前一条半边int next; 后一条半边int opp; 对面相反的半边2.海岸线结构，也即是二叉树。

２ ２ ２ ２ （ ｘ ＝０ ｉ ＋ｙ ｉ －ｘ ｊ －ｙ ｊ）
图 １ 算法基本思想 Ｆ ｉ ． １ Ｂ ａ ｓ ｉ ｃ Ｉ ｄ ｅ ａ ｏ ｆ Ａ ｌ ｏ ｒ ｉ ｔ ｈ ｍ ｇ ｇ
： ， 包 含 属 性： Ｏ ｕ ｔ ｕ ｔ Ｖｉ （ ｉ＝１，２， …，ｎ） ｐ Ｉ Ｄ， Ｖｉ 的 惟 一 标 识 ， 与 ｐ ． Ｉ Ｄ 对 应 ；Ｏ ｖ ｅ ｒ ｌ ａ Ｉ Ｄ， ｐ ｉ Ｖｉ 重叠点的 Ｉ Ｄ 集合 。 ／ ／获取 ｐ Ｇ ｅ ｔ ＭＢ Ｒ ｉ 的最小外矩形 （ ｆ ｏ ｒ ｉ ｎ ｔ ｉ ＝２； ｉ ｎ； ｉ ＋＋ ）｛ ≤ （ ； ｆ ｏ ｒ ｉ ｎ ｔ ｉ ｊ＝１； ｊ＜ ｊ＋＋ ）｛ ／ ／重叠点处理 ｖ ｅ ｒ ｌ ａ ｅ ｄ Ｐ ｎ ｔ ｓ Ｐ ｒ ｏ ｃ Ｏ ｐ ｐ （ ） Ｉ ｆ Ｗ ｅ ｉ ｈ ｔ＝ ｐ Ｗ ｅ ｉ ｈ ｔ ｇ ｇ ｐ ｉ． ｊ． ／ ／ 垂直平分线划分区域 ｉ ｖ ｉ ｄ ｅ Ｒ ｅ ｉ ｏ ｎＷ ｉ ｔ ｈ Ｐ Ｂ Ｄ ｇ ｌ ｓ ｅ Ｅ ／ ／圆弧划分区域 ｝ ｉ ｖ ｉ ｄ ｅ Ｒ ｅ ｉ ｏ ｎＷ ｉ ｔ ｈ Ａ ｒ ｃ Ｄ ｇ ／ ／区域合并 ｝ ｎ ｉ ｏ ｎ Ｒ ｅ ｉ ｏ ｎ Ｕ ｇ ／ ／加权区域重分类 Ｗ ｅ ｉ Ｖ ｏ ｒ Ｃ ｌ ａ ｓ ｓ ｉ ｆ ｉ ｃ ａ ｔ ｉ ｏ ｎ ／ ／加权区域重划分 Ｗ ｅ ｉ Ｖ ｏ ｒ Ｒ ｅ ｉ ｏ ｎ Ｒ ｅ ｄ ｉ ｖ ｉ ｓ ｉ ｏ ｎ ｇ 算法首先获 取 点 集 ｐ ｉ 的 最 小 外 包 矩 形， 作 为 起始点 ｐ １ 的占 有 区 域 ， 然 后 逐 点 插 入 ， 划 分 最 小 外包矩形 。 插入过 程 中 ， 依 次 对 比 新 插 入 点 ｐｍ 与 已插入点ｐ 的位置 ， 如果位置重叠 ， 则进行 ｉ ｎ） ≤ ｉ（ （ ； 否 则， 对 比 两 点 权 重叠 点 处 理 详 见 ２ ． ３ ． １ 节）

空间数据库查询技术
空间数据库
空间数据库是存储和管理空 间数据的数据库系统，通过 空间数据库查询技术可以快 速获取构建Voronoi图所需的
空间数据。
查询优化
空间数据库查询技术通常采 用查询优化技术，以提高查 询效率，减少构建Voronoi图
所需的时间。
数据存储
空间数据库的数据存储方式 对构建Voronoi图的速度和效 率也有影响，合理的数据存 储方式可以提高构建效率。
详细描述
利用Voronoi图对城市商业设施进行空间分析，可以识别出 商业设施的密集区域和稀疏区域，了解各区域商业设施的竞 争状况和服务范围，有助于优化商业布局，提高城市整体商 业发展水平。
地震灾害影响范围评估
总结词
Voronoi图可用于评估地震灾害的影 响范围，通过对受灾区域进行空间分 析，可以快速识别出受灾严重的区域， 为抢险救灾和灾后重建提供决策支持。
计算几何方法
计算几何
计算几何是构建Voronoi图的重要方法之一，通过计算几何 中的几何对象和算法，能够高效地生成Voronoi图。
常用算法
计算几何中常用的算法包括凸包算法、几何扫描算法等， 这些算法能够提高Voronoi图的构建效率。
精度控制
计算几何方法通常需要精度控制，以确保生成的Voronoi图 满足精度要求。
种群密度估计
通过Voronoi图，可以估计动物种群的密度，了解种群分布和数 量。
移动路径分析
Voronoi图可以用于分析动物的移动路径和活动范围，了解动物 的迁徙和行为模式。
04
Voronoi图的实际案例分 析
城市商业设施分布分析
总结词
通过Voronoi图分析城市中商业设施的分布情况，可以发现 商业设施在空间上的聚集程度和分布规律，为城市规划和商 业布局提供决策依据。

接下来，对有限元模型进行网格划分，并根据材料的晶体结构和物理性质设 置相应的本构模型。最后，通过有限元求解器解算方程，得到材料的塑性变形行 为和应力应变曲线。
通过对比不同案例的分析结果，可以得出以下结论： (1)基于Voronoi图的 晶体塑性有限元多晶几何建模能够准确描述材料的塑性变形行为和应力应变曲线。 (2)不同的晶粒尺寸和形状分布会对材料的塑性变形产生影响。较小的晶粒尺寸 和更复杂的晶粒形状会导致材料具有更高的屈服强度和塑性变形能力。
基于图论的图像分割嵌入式应用
基于图论的图像分割技术在许多嵌入式应用中都发挥着重要的作用。下面我 们列举几个典型的例子：
1、无人驾驶汽车
无人驾驶汽车是近年来研究的热点之一。在无人驾驶汽车中，基于图论的图 像分割技术可以用于识别和区分道路上的各种对象，如车辆、行人、交通标志等。 此外，还可以利用图论中的路径规划算法来制定行驶路径，确保车辆的安全行驶。
1、图像处理：在图像处理中，Voronoi图可用于图像分割、特征提取和图像 增强等方面。例如，将图像中的像素点作为输入点集，通过计算距离和插值，生 成Voronoi图，进而实现图像分割和特征提取。
2、数据挖掘：在数据挖掘中，Voronoi图可用于聚类分析、关联规则挖掘和 频繁项集挖掘等方面。通过将数据点作为输入点集，生成Voronoi图，可以更好 地理解数据分布和结构，从而发现隐藏在数据中的有用信息。
2、简化模型建立：无需手动创建复杂的几何模型，而是通过自动生成的多 晶几何模型进行模拟和分析。
3、优化计算效率：通过使用高效的有限元算法和计算机集群，可以大幅缩 短计算时间。
案例分析
以一个多晶铜材料的晶体塑性有限元分析为例，详细介绍如何基于Voronoi 图的晶体塑性有限元多晶几何建模。首先，根据实验测量的晶粒尺寸和形状分布， 创建代表晶粒的点集合，并生成Voronoi图。然后，将Voronoi图导入有限元分析 软件中，建立有限元模型。在设置边界条件时，需考虑材料的固定约束和加载条 件。

多 边 形 与 弧 段 ： P2 与 L3,L5,L2
2）邻接性： (同类元素之 间)
多边形之间、结点之间。
邻接矩阵
重叠：-- 邻接：1 不邻接： 0
P1 P2 P3 P4 P1 -- 1 1 1 P2 1 -- 1 0 P3 1 1 -- 0 P4 1 0 0 --
3）连通性：与邻接性相类似，指对弧段连接的判别，如用于网络 分析中确定路径、街道是否相通。
连通矩阵： 重叠：-- 连通：1 不连通：0
V1 V2 V3 …
V1 -- 1 0 V2 1 -- 1 V3 0 1 --
4）拓扑包含：指面状实体包含了哪些线、点或面状实体。
主要的拓扑关系：拓扑邻接、拓扑关联、拓扑包含。
P2
P1
P2
P3 P2
P1 P1
P2
拓扑关系的表达 拓扑关系具体可由4个关系表来表示： （1） 面--链关系： 面 构成面的弧段 （2） 链--结点关系： 链 链两端的结点 （3） 结点--链关系： 结点 通过该结点的链 （4） 链—面关系： 链 左面 右面
2 杨树 x1, y1；x2, y2；…； 林 xn, yn; x1, y1
3 松树 x1, y1；x2, y2；…； 林 xn, yn; x1, y1
空间对象的矢量数据模型
3.4 空间逻辑数据模型
二、栅格数据模型
在栅格数据模型中，点实体是一 个栅格单元（cell）或像元，线实体 由一串彼此相连的像元构成，面实 体则由一系列相邻的像元构成，像 元的大小是一致的。
象）
分类
子类/超类 等效
空间关系 非空间关系 时间关系
地理空间 空间要素
几何坐标
子部分 超部分
非空间属性

2
2010， 46 （22）
Computer Engineering and Applications 计算机工程与应用
状， 以及该形状对于求解最短路径的影响。 在上述文献中建立的 Voronoi 图， 都将障碍物简化为一个 点， 而忽略了障碍物边界形状对于路图通道宽度的影响。但 是在拥挤的环境中， 障碍物边界形状复杂， 需要使用广义 Voronoi 图来抽象表示拥挤的空间环境。 Kalra 等[7]提出了一种基于网格点的增量算法用于构造广 义 Voronoi 图， 用于机器人规划路径。吴海彬等 针对移动机
图1
Quad-Edge 数据结构及其基本 操作： rot， sym， next
的点不能很好地表示复杂障碍物， 需要使用多边形表示复杂 障碍物。为了对具有多边形障碍物的空间环境进行抽象， 需 要使用广义 Voronoi 图来描述。在通常由离散点生成的 Voronoi 图中只包含有直线段， 然而在广义 Voronoi 图中的边包含 有抛物线和直线。这是由于在生成 Voronoi 图的过程中， 有三 种不同的 Voronoi 边的生成情况。每一个二维的障碍物， 可以 表示为凸多边形和凹多边形， 利用直线作为边界， 点作为角。 当 Voronoi 边距离两个障碍物的边界 （线－线） 、 或者两个障碍 物的转角 （点－点） 距离相等时， 将生成直线段。然而， 当 Voronoi 边距离一个障碍物的转角和另一个障碍物的边界 （点－ 线） 距离相等时， 将会生成抛物线。生成这样的具有抛物线和 直线的 Voronoi 图是很困难的。即使生成了非常精确的广义 Voronoi 图， 也不得不通过线段来近似描述每个抛物线， 从而 生成机器人运动控制可以使用的命令。 Okabe， Boots 和 Sugihara[13] 提出了一个非常有效的近似方法用于找到一组二维障 碍物的广义 Voronoi 图， 通过将障碍物边界离散化为多个点， 从而获取具有二维障碍物空间的广义 Voronoi 图。 在通常的广义 Voronoi 图生成方法中， 将障碍物的边界通 过 Minkowski 和的方法膨胀一半机器人宽度， 获取允许一辆 小车通过的广义 Voronoi 图， 从而将多边形机器人的路径规划 问题转化为点机器人的情况， 然而此方法并不适用于多机器 人运动规划问题的求解。在多机器人运动规划中， 当两个机 器人相向通过同一通道时， 如果通道宽度允许两个机器人同 时并排通过， 则可以由交错的方式通过该通道， 如果通道宽度 只允许一个机器人通过， 则必须有一个机器人在通道外等待 另一个机器人通过之后， 才能通过该通道。所以计算通道的 宽度在多机器人运动规划中是非常必要的， 通道宽度的不同， 机器人通过通道时所采取的策略也不同。为此提出了一种计 算广义 Voronoi 图及其通道宽度的算法， 算法步骤如下。 （1） 通过将原始多边形的边界分割成许多小线段， 多边形 障碍物的边界可以近似为大量的点。这样， 就获得了表示多 边形障碍物的一组离散点。 （2） 对得到的离散点进行 Delaunay 三角剖分。在此采用 增量方法， 逐个添加顶点到图中， 并采用 Quad-Edge 表示三角 形的边。 （3） 得到 Voronoi 图及其通道的宽度。 对于得到的 Delaunay 三角剖分中的每个三角行的每条边 执行下面的操作。 ①获得与该边相关联的左边三角形的所有的顶点。计算 该三角形的外接圆的圆心， 作为 Voronoi 边的器人运动规划问题中， 需要即时规划出多移