下载文档原格式
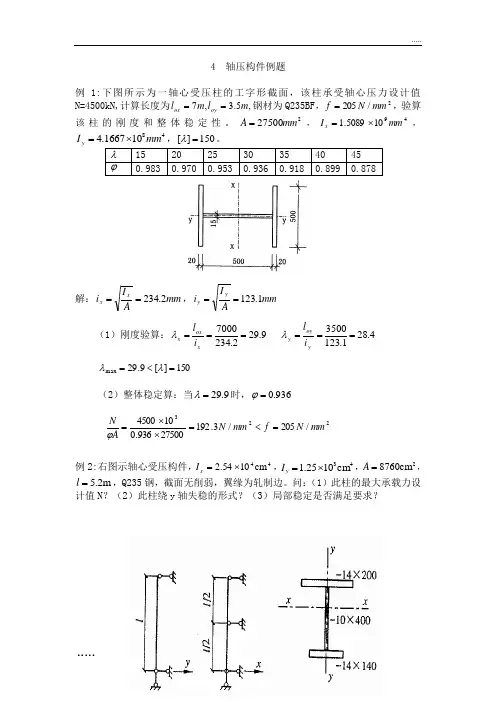
4 轴压构件例题例1:下图所示为一轴心受压柱的工字形截面，该柱承受轴心压力设计值N=4500kN,计算长度为,5.3,7m l m l oy ox ==钢材为Q235BF ，2/205mm N f =，验算该柱的刚度和整体稳定性。
227500mm A =，49105089.1mm I x ⨯=，48101667.4mm I y ⨯=，150][=λ。
λ 15 20 25 30 35 40 45 ϕ0.983 0.970 0.953 0.936 0.918 0.899 0.878解：mm AI i xx 2.234==，mm AI i y y 1.123==（1）刚度验算：4.281.12335009.292.2347000======yoy y x ox x i l i l λλ 150][9.29max =<=λλ（2）整体稳定算：当9.29=λ时，936.0=ϕ223/205/3.19227500936.0104500mm N f mm N A N =<=⨯⨯=ϕ例2:右图示轴心受压构件，44cm 1054.2⨯=x I ，43cm 1025.1⨯=y I ，2cm 8760=A ，m 2.5=l ，Q235钢，截面无削弱，翼缘为轧制边。
问：（1）此柱的最大承载力设计值N ？（2）此柱绕y 轴失稳的形式？（3）局部稳定是否满足要求？解：（1）整体稳定承载力计算 对x 轴：m2.50==l l x ，cm 176.871054.24=⨯==A I i x x 150][6.30175200=≤===λλx x x i l 翼缘轧制边，对x 轴为b 类截面，查表有：934.0=x ϕkN 1759102158760934.03=⨯⨯⨯==-Af N x x ϕ 对y 轴： m6.22/0==l l y ，cm 78.36.871025.13=⨯==A I i y y 150][8.6878.35200=≤===λλy y y i l翼缘轧制边，对y 轴为c 类截面，查表有：650.0=y ϕkN 122410215876065.03=⨯⨯⨯==-Af N y y ϕ 由于无截面削弱，强度承载力高于稳定承载力，故构件的最大承载力为：kN 1224max ==y N N （2）绕y 轴为弯扭失稳（3）局部稳定验算8.68},max {max ==y x λλλ，10030max ≤≤λ1） 较大翼缘的局部稳定y f t b 235)1.010(79.614/95/max 1λ+≤==88.16235235)8.681.010(=⨯+=，可2） 腹板的局部稳定y w f t h 235)5.025(4010/400/max 0λ+≤==4.59235235)8.685.025(=⨯+=，可例3:下图所示轴心受压格构柱承受轴力设计值N=800kN ，计算长度l ox =l oy =10m ，分肢采用2［25a ：A=2×34.91＝69.82cm 2，i y =9.81cm,I 1=175.9cm 4，i 1=2.24cm ，y 1=2.07cm ，钢材为Q235BF ，缀条用L45×4，A d =3.49cm 2。
钢结构受弯构件_附答案时磊忖呎…7.当梁上有固定较大集中荷载作用时，其作用点处应（B ）。
A ）设置纵向加劲肋B ）设置横向加劲肋C ）减少腹板宽度D ）增加翼缘的厚度X 8焊接组合梁腹板中，布置横向加劲肋对防止（A ）引起的局部失稳最有效，布置纵向加劲肋对防止（B ）引起的局部失稳最有效。
A ）剪应力B ）弯曲应力D ）复合应力D ）局部压应力X 9 .确定梁的经济高度的原则是（B ）。
A ）制造时间最短 C ）最便于施工B ）用钢量最省 D ）免于变截面的麻烦X 10 .当梁整体稳定系数抵〉0.6时，用$'弋替啟主要是因为（B ）A ）梁的局部稳定有影响B ）梁已进入弹塑性阶段C ）梁发生了弯扭变形D ）梁的强度降低了XX 11.分析焊接工字形钢梁腹板局部稳定时，腹板与翼缘相接处可简化为（练习五受弯构件、选择题（X 不做要求） 1计算梁的（ A ）时，应用净截面的几何参数。
A ）正应力 B ）剪应力 C ）整体稳定 M x 2 ?钢结构梁计算公式 -中，Y （ C ）。
x W nx A ）与材料强度有关 B ）是极限弯矩与边缘屈服弯矩之比 C ）表示截面部分进人塑性 D ）与梁所受荷载有关D ）局部稳定XX ?在充分发挥材料强度的前提下, Q235钢梁的最小咼度 h min （ C ） Q345钢梁的h min（其他条件均相同）A ）大于B ）小于 X 4 .梁的最小高度是由（C A ）强度 B ）建筑要求 5. 单向受弯梁失去整体稳定时是（ A ）弯曲 B ）扭转 6. 为了提高梁的整体稳定，（B C ）等于D ）不确定）控制的。
C ）刚度 D ）整体稳定 C ）失稳。
C ）弯扭 D ）都有可能）是最经济有效的办法。
A ）增大截面 B ）增加支撑点，减小11C ）设置横向加劲肋D ）改变荷载作用的位置D ）。
1------------------- 布磊5『彳 ----- ----- ---- --------------------A ）自由边B ）简支边C ）固定边D ）有转动约束的支承边x %2 .梁的支承加劲肋应设置在（ C ） oA ）弯曲应力大的区段B ）剪应力大的区段C ）上翼缘或下翼缘有固定荷载作用的部位D ）有吊车轮压的部位13?双轴对称工字形截面梁，经验算，其强度和刚度正好满足要求，而腹板在弯曲应力作用下有发生局部失稳的可能。
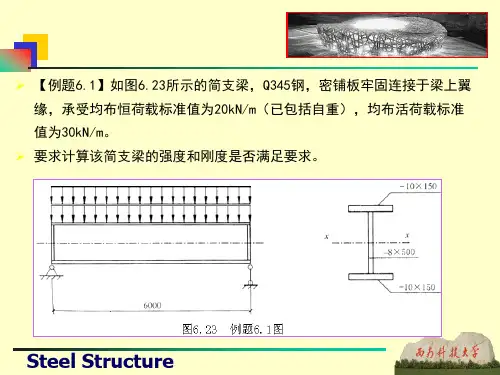
受弯构件一.强度计算（抗弯、抗剪、局部承压、复杂应力）1.已知简支轨道梁承受动力荷载，其最大弯矩设计值Mx=440KNm，采用热轧H 型钢H600×200×11×17制作，Ix=78500×104mm4，W nx=W x=2610×103mm3，钢材为Q235。
验算受弯承载力。
2.抗剪强度计算例题：某焊接工字形等截面简支楼盖梁，截面尺寸如图所示，无削弱，为Q345钢。
梁的剪力设计值：支座截面V max=224.22KN，跨中截面处V=214.5KN。
要求验算该梁的抗剪强度。
3.局部承压强度计算例题：某热轧普通工字钢简支梁如图所示，型号为I36a，跨度为5m，梁上翼缘作用有均布荷载其设计值为q=36KN/m（包括自重），该梁为支承于主梁顶上的次梁，未设加劲肋。
支承长度a=100mm，t w=10mm，h y=t+r，此处t=15.8mm，r=12.0mm，钢材为Q235，f=215N/mm2。
验算此梁的局部承压强度。
4.复杂（折算）应力强度的计算例题：如图所示一焊接组合截面吊车梁，钢梁截面尺寸如图所示。
吊车为重级工作制（A7），吊车轨道型号为QU100，轨道高度为150mm，吊车最大轮压F=355KN，吊车竖向荷载动力系数为1.1，可变荷载分项系数为1.4，车轮作用处最大弯矩设计值为M=4932KNm，对应的剪力设计值为316KN，吊车梁采用Q345-B钢，I nx=2.433×1010mm4。
求车轮作用处钢梁的折算应力。
二．整体稳定计算1.轧制工字钢梁的整体稳定计算例题：某轧制工字钢简支梁，型号为I50a，Wx=1860cm3，跨度为6m，梁上翼缘作用均布永久荷载g k=10KN/m（标准值，含自重）和可变荷载q k=2510KN/m （标准值），跨中无侧向支承。
钢材为Q235。
验算此梁的整体稳定。
例题：一焊接工字形截面简支主梁如图所示，截面无扣孔，跨度为12.75m。
6-3、图示矩形截面梁受集中力作用，试计算1-1横截面上a 、b 、c 、d 四点的正应力。
解：（1）外力分析，判变形。
荷载在纵向对称面内，与轴线垂直，梁发生平面弯曲。
中性轴z 轴过形心C 与载荷垂直，沿水平方向。
（2）内力分析，弯矩图如图（b ）所示，1-1横截面的弯矩为：1115230(M -=-⨯=-⋅kN m)（3）应力分析，梁上边有弯矩图，上侧纤维受拉。
1-1横截面上的a 点处于拉伸区，正应力为正；c 点处于中性层上，正应力为零；b 、d 两点处于压缩区，正应力为负。
3111111max2301011.1110.1800.36a a zzzM M M y y I I W σ---⨯=⋅=⋅===⨯⨯Pa MPa 。
11.11b a σσ=-=-MPa0c σ= 31133010(0.1500.050)7.4110.1800.312d d zM y I σ-⨯=-⋅=-⨯-=-⨯⨯Pa MPa37M kN V 图(kN)(a)(c)(b)(c)(e)(d)2+q l /8MkN ·m)(f)(b)180q题6-3图 题6-5图6-5、两根矩形截面简支木梁受均布荷载q 作用，如图所示。
梁的横截面有两种情况，一是如图(b)所示是整体，另一种情况如图(c)所示是由两根方木叠合而成（二方木间不加任何联系且不考虑摩擦）。
若已知第一种情况整体时梁的最大正应力为10MPa ，试计算第二种情况时梁中的最大正应力，并分别画出危险截面上正应力沿高度的分布规律图示。
解：（1）外力分析，判变形。
荷载在纵向对称面内，与轴线垂直，梁发生平面弯曲。
第一种情况中性层为过轴线的水平纵向面，中性轴z 轴过整体形心C 与载荷垂直，沿水平方向。
而第二种情况，两根木梁以各自的水平纵向面为中性层发生弯曲，两根中性轴为与荷载垂直的水平形心主轴。
如图所示。
（2）内力分析，判危险面：弯矩图如图（b ）所示，跨中截面为危险面。
第六章 例题【例题6.3】校核如图6.19所示双轴对称焊接箱形截面压弯构件的截面尺寸，截面无削弱。
承受的荷载设计值为：轴心压力880=N kN ，构件跨度中点横向集中荷载180=F kN 。
构件长10=l m ，两端铰接并在两端各设有一侧向支承点。
材料用Q235钢。
图6.19 例6.3图【解】构件计算长度1000==y x l l m ，构件段无端弯矩但有横向荷载作用，弯矩作用平面内外的等效弯矩系数为4504/)10180(4/,0.1=⨯====Fl M x tx mx ββkN·m 。
箱形截面受弯构件整体稳定系数0.1=b ϕ，因4510/450/,6.2314/330/0====w w t h t b ，均大于20，故焊接箱形截面构件对x 轴屈曲和对y 轴屈曲均属b 类截面。
一、截面几何特性 截面积：1880.14524.135222=⨯⨯+⨯⨯=+=w w t h bt A cm 2惯性矩：6795112/)45338.4735(12/)(33303=⨯-⨯=-=wx h b bh I cm 4 3602212/)3345358.47(12/)(33303=⨯-⨯=-=b h hb I w y cm 4回转半径：01.19188/67951/===A I i x x cm ，84.13188/36022/===A I i y y cm弯矩作用于平面内受压纤维的毛截面模量：28438.47/679512/2=⨯===h I W W x x 1x cm 3二、验算截面1.在弯矩作用平面内的稳定： 6.5201.1910000===x x x i l λ ＜[]150=λ（满足）。
查附表4.2，844.0=x ϕkN EAN xEx 12559106.521.110188102061.13223222'=⨯⨯⨯⨯⨯⨯==-πλπ截面截面塑性发展系数05.1=x γ，等效弯矩系数0.1=mx β。
