专题二 函数概念与基本初等函数 第六讲函数综合及其应用答案
- 格式:doc
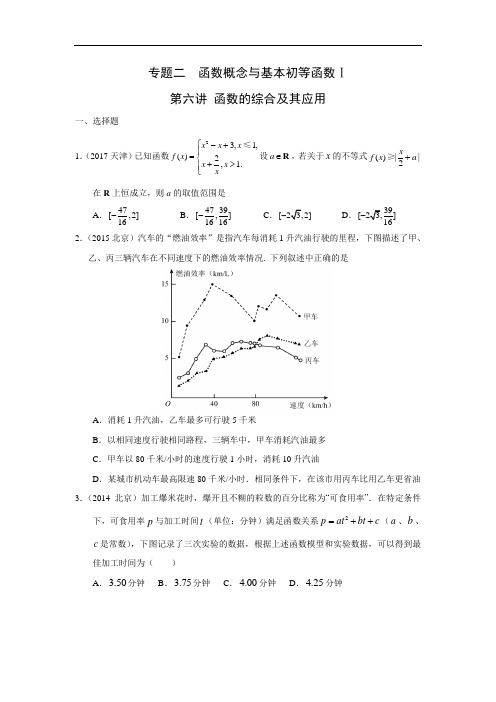
- 大小:901.16 KB
- 文档页数:8

函数及函数综合应用 一、函数的表示(分段函数)【典型例题】例1.1 设 f (x )={x +1,x ≤02x , x >0 ,则满足f(x)+f (x -12)>1的x 的取值范围是 .【答案】(-14,+∞) 【解析】当x ≥12时:显然成立; 当12≥x >0时:f(x)+f (x -12)=2x +x -12+1>1,成立 当x <0时:f(x)+f (x -12)= x +1+x -12+1>1,解得x >-14【要点】分段函数处理方法一:分段解析例1.2 设f(x)=⎪⎩⎪⎨⎧≥-+-<<-2,8620,22x x x x x x,若两两不相等的正数a 、b 、c 满足f(a)=f(b)=f(c),则:(1) a+b+c 的取值范围是 . (2) abc 的取值范围是 . 【答案】(1) (7,8) (2) (9,16)【解析】(1)作出y=f(x)的图像,不妨设a<b<c ,则显然0<a <2<b <3<c <4,由对称性b+c =6,由x =3的y max =1,此时x =1,a ∈(1,2);,a+b+c ∈(7,8)(2)设y=t ,(0<t <1) 则,a =, b 、c 是方程-x 2+6x -8=t 的两根,由韦达定理bc =8+t ,abc ==∈(9,16) 【要点】(1)图像是研究分段函数重要的辅助工具(2)多变量目标函数求范围,要点是研究多个变量之间的关系,将目标函数化为一个变量的函数例1.3 已知函数f (x )=220ln(1)0.x x x x x ⎧-+≤⎨+>⎩,,, 若|f (x )|≥ax ,则a 的取值范围是 .【答案】[-2,0]【解法一】由y =|f (x )|的图象知:①当x >0时,y =ax 只有a ≤0时,才能满足|f (x )|≥ax . ②当x ≤0时,y =|f (x )|=|-x 2+2x |=x 2-2x .a 的下界为抛物线y= x 2-2x 在(0,0) 处的切线斜率故由y’=2x -2知k 切线=-2,∴ a ≥-2. 综上可知:a ∈[-2,0].∴∴a t a =-212+t ∴1)8(2++t t 2114++t【解法二】x >0时,g(x)=|f (x )|-ax =ln(x +1)-ax ,当a >0时:x →+∞时g(x) →−∞,不符题意 当a ≤0时:g(x)为增函数,g(x)>g(0)=0,符合题意x ≤0时,g(x)=|f (x )|-ax =x 2-2x -ax =x (x -(a +2))≥0,即x -(a +2)≤0,故a ≥x -2,由x ≤0知a ≥-2例1.4 用min {a,b }表示a,b 两个数中的较小值,用max {a,b }表示a,b 两个数中的较大值,设f(x)=x 2-2(a +2)x +a 2,g(x)=-x 2+2(a -2)x -a 2+8. 令H 1(x )=max {f(x),g(x)},记H 1(x )的最小值为A ;令H 2(x )=min {f(x),g(x)},记H 2(x )的最大值为B ;则A -B=【答案】-16【解析】令f(x)=g(x)可解得x =a +2和x =a -2作出f(x)及g(x)的图像,由图像可知:A =(H 1(x ))min =f (a +2);B =(H 2(x ))max =f (a -2) 所以A -B=-16【要点】分段函数处理方法二:图像法二、函数性质及应用【典型例题】例2.1 以下命题中,正确的有 (填出所有正确的命题的序号)① 函数f(x)=-|x -1|+1 的图象关于直线x =1对称,且当 x >1时为减函数 ② 函数f(x)=2x −12x +1为奇函数,且在R 上为增函数③ 函数f(x)=lg x -lg(2-x )+2的图象关于点(1,2)对称,且在(0,2)上为增函数 ④ 所有二次函数的图象都是轴对称图形;所有三次函数的图象都是中心对称图形⑤ 函数1sin )1()(22+++=x xx x f 的图象关于点(0,1)对称 【答案】12345【解析】(1) 作图可知正确(2) 可验证f(x)+f(-x)=0,函数y =t−1t+1=1-2t+1(t >0) 和t =2x 都是增函数 (3) 可验证:f(x)+f(2-x)=4,函数y = lg x 和y =-lg(2-x )都是增函数 (4) 正确 (5) f(x)=1sin 212+++x xx (奇函数+1)【要点】对称性的验证和发现例2.2 若0<a <b <1,则以下命题中,正确的是 (填出所有正确的命题的序号) ① a b <a a ② a a <b a ③ ba a >ab a ④ a b <b a ⑤ a a <b b【答案】1234【解析】(1) 令f(x)=a x 为减函数,则f(a)>f(b),即a b <a a (2) 令f(x)=x a 为增函数,则f(a)<f(b),即a a <b a (3) 令f(x)=x a -1 为减函数,则f(a)>f(b),化简得ba a >ab a(4) 令f(x)=lnx x,由f(x)导数可得f(x)在(0,e)为增函数,则f(a)<f(b),即lna a<lnb b所以blna<alnb ,即a b <b a(5) 令f(x)=xlnx , 由f(x)导数可得f(x)在(0,e -1)为减函数,(e -1,1)为增函数,故f(a)、f(b)的大小不定 即a a 、b b 大小不定【要点】构造函数,利用函数单调性比较大小例2.3设⎪⎩⎪⎨⎧>+≤-=0,0,2)(22x bx ax x x x x f ,若f(x)是偶函数,则使得f (3x -2)>f (x 2)的x 的取值范围是【答案】(−3+√172,3)【解析】y=x 2-2x 在x <0时为减函数,而f(x)图像关于y 轴对称,故原不等式等价于: |3x -2|>|x 2|,解得答案【要点】单调性+对称性在不等式中的应用例2.4 设函数f(x)=|)|1ln(112x x +-+,则使得f(x)>f (2x -1)的x 的取值范围是 . 【答案】(-∞,13) ∪ (3,+∞)【解析】注意到f(x)为偶函数,当x >0时,f(x)=)ln(1112x x +-+为减函数, 故原不等式等价于: |x |<|2x -1|,解得答案 【要点】单调性+对称性在不等式中的应用例2.5设f(x)=x 2-2x +a (e x -1+e 1-x ) 恰有1个零点,则a = 【答案】12【解析】注意到f(x)=f (2-x ),即f(x)图像关于x =1对称,所以f (1)=0解得 【要点】主动发现f(x)的对称性注意函数g(x)=f(x -m)+f(m -x) 具有轴对称性 g(x)=f(x -m)-f(m -x )具有中心对称性 本题也有其他解法,但用对称性解决是最快捷的方法例2.6 已知函数f(x)满足f (-x )=2-f(x),若函数xx y 1+=与y=f(x)图像的交点为(x 1,y 1),(x 2,y 2)……(x m ,y m ),则=+∑=mi i iy x1)(A.0B. mC. 2mD. 4m 【答案】B【解析】f (-x )=2-f(x)表明f(x )图像关于(1,0)中心对称,而xx y 1+=图像也关于(1,0)中心对称, 所以两个函数的图像的公共点也关于(1,0)中心对称 【要点】对称性的应用例2.7 设a >0,b >0,e 是自然对数的底数,则( )A .若e a +2a =e b +3b ,则a >bB .若e a +2a =e b +3b ,则a <bC .若e a -2a =e b -3b ,则a >bD .若e a -2a =e b -3b ,则a <b 【答案】A【解析】令f(x)= e x +2x 为增函数,则f(a)=f(b)+b>f(b),所以a>b C 、D 可通过g (x)= e x -2x 的单调性判定 【要点】构造函数,通过单调性研究方程与不等式三、函数图像及图像变换【典型例题】例3.1将函数y=f(x)的图像左移1个单位、再将横坐标变成原来的2倍 (纵坐标不变),得到函数y=g(x)的图像,已知函数y=g(x)的图像与函数y =ln(x +1)的图像关于y 轴对称,则函数y=f(x)的解析式为( ) A. ln(2x -1) B. ln(-2x +3) C. ln(x +) D.ln(-x -2) 【答案】B【解析】将y =ln(x +1)对称得到g(x),再逆变换:横坐标变成原来的倍、右移1个单位得到f(x): g(x)=ln(-x +1),g(x)→g (2x )=ln(-2x +1)→ln(-2(x -1)+1)= ln(-2x +3)【要点】逆变换例3.2 设函数y=f(x)的图像与y =2log 2(x +a )-2的图像关于直线y =-x 对称,且f (2)+f (0)=3,则a = . 【答案】3【解析】-x =2log 2(-y +a )-2,解得y=a -222+-x ,即为f(x)的解析式f (2)+f (0)=2a -3=3,a =3 【要点】重要的对称变换例3.3 若实数m 、n 满足m +2m =5,n +log 2n =5,则一定有( )A. m+n >5B. m+n =5C.m+n <1D. m+n =1 【答案】B【解析】令f(x)=2x ,g(x)=log 2x ,则f(x)、g(x)图像关于y=x 对称m +2m =5化为2m =5-m ,即直线y =5-x 与f(x)的公共点为(m ,5-m ) 同理直线y =5-x 与g(x)的公共点为(n ,5-n )由于直线y =5-x 与y=x 垂直,所以两个公共点关于y=x 对称,即m =5-n 【要点】主动发现两个函数图像的对称性21212121例3.4 函数y =x cos x +sin x 的图象大致为( ).【答案】D【解析】f’(x)=2cosx -xsinx ,f’(0)=2,f’(π)<0;【要点】导数、切线、极限、渐近线等在图像识别中的应用例3.5 函数y =x x xx ee e e ---+的图象大致为( )【答案】A【解析】方法很多,例如奇函数+单调性;也可考虑渐近线例3.6函数y =f (x )的图象如图所示,在区间[a ,b ]上可找到n (n ≥2)个不同的数x 1,x 2,…,x n ,使得1212===n nf x f x f x x x x ()()(),则n 的所有可能的取值组成的集合为 ( ).A .{3,4}B .{2,3,4}C .{3,4,5} D.{2,3}【答案】B【解析】为图像上一点(x ,f(x))与原点连线的斜率,观察图像即可得到答案【要点】图像的几何意义xx f )(四、函数应用(不等式、方程)【典型例题】例4.1 当0<x ≤12时,4x <log a x ,则a 的取值范围是 【答案】(22,1) 【解析】当a >1时:4x >1,log a x <log a12<0,不成立 当0<a <1时:g(x)= 4x -log a x 为增函数,g(x)<0恒成立等价于:g (12)<0,解得答案 【要点】分类讨论例4.2 设a >41,若不等式|x 2-2ax -3a 2|≤4a 对任意x ∈[1,4a ]恒成立,则a 的取值范围是 【答案】(41,]【解析】设f(x)= |x 2-2ax -3a 2|=|(x -3a )(x +a )|;由绝对值及二次函数性质知,f(x)在(-∞,-a )减,(-a ,a )增,(a ,3a )减,(3a ,+∞)增 由f (1)=|3a 2+2a -1|≤4a ,得a ≤1;故∴ f(x)max =max {f (1),f (4a )},于是f(x)max ≤4a 等价于 解得答案【要点】二次函数、绝对值函数;图像法例4.3 若x ∈[-2,1],ax 3-x 2+4x +3≥0,则a 的取值范围是 . 【答案】[-6,-2]【解析】x =0时显然成立;-2≤x <0时原不等式等价于a ≤ 令g(t)=-3t 3-4t 2+t (t ≤-),则g(t)min =g (-1)=-2,故a ≤-2 同理,0<x ≤1时a ≥g(t) (t ≥1),g(t)max =g (1)=-6,故a ≥-6 【要点】不等式预处理—参数分离,但要合理使用 (不是万能手段)例4.4 若函数f(x)=3x -sin2x +3a sin x 在R 上单调递增,则a 的取值范围是【答案】[-31,31]【解析】原命题等价于:f’(x)≥0在R 上恒成立;f’(x)= 3-2cos2x +3a cos x =-4cos 2x +3a cos x+5考虑g(t)=-4t 2+3at+5 (-1≤x ≤1),则g(t)min =min{g (-1),g (1)}故g(t)≥0恒成立等价于⎩⎨⎧≥≥-0)1(0)1(g g ,可解得答案【要点】变量替换54⎪⎩⎪⎨⎧≤=≤-+=aa a f aa a f 45)4(4|123|)1(22xx x x x x 1)1(4)1(3342332+--=--21例4.5 f(x)=2x |log 0.5x |-1的零点个数是 . 【答案】2【解析】分别作出曲线y =|log 0.5x |和曲线y =2-x 的图像 【要点】研究零点的技巧:预处理例4.6 函数f(x)=e x (2x -a )+1有零点,则a 的取值范围是 . 【答案】[2-2ln2,+∞)【解析】f’(x)= e x (2x -a +2),故f(x)在(-∞,22-a )为减,(22-a ,+∞) 为增 x →+∞时 f(x)→+∞故f(x)有零点的充要条件为:f (22-a )≤0,解得答案 【另解】分别作出y =-e -x 和y =2x -a 的图像,当直线y =2x -a 与曲线y =-e -x 相切时, (-e -x )’=e -x =2,解得x =-ln2,y =-2,即为切点坐标带入直线可解得此时-a =2ln2-2由图像可知,当直线向下移动式满足条件,故-a ≤2ln2-2,即得 【要点】研究零点的方法:(1) 单调性+零点定理 (2) 图像法例4.7 已知函数f (x )=ax 3-3x 2+1,若f (x )存在唯一的零点x 0,且x 0>0,则a 的取值范围是( ).A .(2,+∞)B .(1,+∞)C .(-∞,-2)D .(-∞,-1) 【答案】C【解析】f’(x)=3x (ax -2)当a <0时:f(x)在(-∞,2a )减,( 2a ,0)增,(0,+∞)减依题意:f (2a)>0,解得a <-2当a =0时:f(x)有两个零点不符题意;当a >0时:f(x)在(-∞,0)增, (0,2a)减,(2a,+∞)增,而f (0)=1>0,不符题意【要点】三次函数的零点例4.8 设a >1,f(x)=a x ,若存在实数T ,使得对任意实数x 都有f (x +T )=Tf (x ),则a 的取值范围是 【答案】(1,e1e ]【解析】f(x+T)=a T a x =Ta x ,即存在T ,使得a T =T ;即T ln a =ln T ,ln a =TTln , 考虑函数g(x)=x x ln ,g’(x)=2ln 1x x -=0得x =e ,故g(x)max =g (e)=e 1,所以ln a ≤e1,解得a ≤e 1e例4.9 设a >1,若有且仅有一个常数c 使得对任意的x ∈[a ,3a ],都有y ∈[a , a 2]满足方程log a x+log a y=c ,这时a 的取值的集合为 . 【答案】{3}【解析】log a x+log a y=c 等价于y =,当x ∈[a ,3a ]时,y ∈[,]xa c 131-c a 1-c a依题意即2+log a 3≤c ≤3依题意,满足条件的c 只有1个,所以log a 3=1,a =3例4.10设函数π()x f x m=,若存在f (x )的极值点x 0满足22200+[()]x f x m <,则m 的取值范围是 . 【答案】(-∞,-2)∪(2,+∞) 【解析】∵x 0是f (x )的极值点,0ππcos 0x m m =,即012x mk m =+,k ∈Z. ∴x 02+[f (x 0)]2<m 2可转化为2221π122mk m mk m m m ⎤⎛⎫⎛⎫+++< ⎪⎪⎥⎝⎭⎝⎭⎦,k ∈Z , 即存在k ∈Z ,使221312k m ⎛⎫+<- ⎪⎝⎭;而212k ⎛⎫+ ⎪⎝⎭的最小值为14,∴23114m ->,解得m <-2或m >2.例4.11 设函数()(21)xf x e x ax a =--+,其中1a <,若存在唯一的整数0x ,使得0()0f x <,则a 的取值范围是 【答案】[32e,1)【解析】注意到f (0)= a -1<0,所以原命题成立的一个必要条件为:f (-1)≥0,解得 a ≥ 32e当x ≥1时f’(x)=e x (2x +1)-a >3e -a >0,故f(x)在(1,+ ∞)为增函数,x ≥1时f(x)≥f (1)=e >0当x <-1时f’(x)=e x (2x +1)-a <-e x -a <0,f(x)为减函数,所以f(x)>f (-1)≥0 所以存在唯一的整数0满足题设 【要点】整数命题:探究—证明【思考】若去掉条件a <1,本题如何解答?【提示】考虑预处理:参数分离 注意到f (1)=e>0, 令g(x)= e x (2x−1)x−1 则当x <1时f(x)<0等价于a < g(x);当x >1时f(x)<0等价于a > g(x);g'(x)=e x x(2x−3)(x−1)2 g(x)在(-∞,0)增, (0,1)减,(1,32)减,(32,+∞)增g (0)=1,g (32)=4e32>1,存在唯一的整数x 0<1使得a < g(x 0)的充要条件为:g (-1)≥a >g (0),解得32e≥a >1(此时对任意x >1都有g(x)> g (32)=4e32>a )存在唯一的整数x 0>1使得a > g(x 0)的充要条件为:g (3)≥a >g (2),解得5e 32≥a >3e 2(此时对任意x<1都有g(x)< g (0)=1<a )例4.12 设f(x)=,g(x)=x 2-4x -4,若∃a 使得f(a)+g(b)=0,则b 的取值范围是 . ⎪⎩⎪⎨⎧≤≥--21131a a a a c c ⎪⎪⎩⎪⎪⎨⎧-≥+-<+21),1ln(21,122x x x x x【答案】(-1,5)【解析】当x ∈(-∞,-)时f(x)=(+1)2-1∈(-1,0);当x ∈[-,+∞)时f(x)=ln(x +1)∈[-ln2,+∞),故f(x)∈(-1,+∞)∴g(b)=-f(a)<1,即b 2-4b -4<1 ⇒ b ∈(-1,5). 【要点】∃a 、b ,使得f(a)=g(b)的充要条件为:① f(a) 在函数g(x)的值域内 ② g(b) 在函数f(x)的值域内五、导数及导数的简单应用【典型例题】例5.1 设f(x)为偶函数,当x ≤0时f(x)= e -x -1-x ,则曲线y=f(x)在点(1,f (1))处的切线方程为【答案】y =2x【解析】x ≤0时f’(x)=-e-x -1-1,由f(x)为偶函数可得:f (1)=f (-1)=2,f’(1)=-f’(-1)=2 切线为:y -2=2(x -1)例5.2 若存在直线与曲线y =ln x 和曲线y =x 2+2x +a (x <0)都相切,则a 的取值范围是 . 【答案】(-ln2-1,+∞)【解析】f’(x)= 1x (x >0),g’(x)=2x +2 (x <0)设切点分别为A(s ,f(s))、B(t ,g(t)),则AB 与两条曲线都相切的充要条件为:f’(s)= g’(t)= f (s )−g(t)s−t ,带入:lns−(t 2+2t+a)s−t=1s=2t +2消去s 并化简得:t 2-ln(2t +2)-1=a由s >0解得-1<t <0,令h(t)= t 2-ln(2t +2)-1,则h ’(t)= 2t (t+1)−1t+1<0,故h(t)为减函数所以h(t)的值域为(-ln2-1,+∞) 【要点】公切线的研究方法:f’(s)= g’(t)= f (s )−g(t)s−t例5.3 已知a >0,已知曲线C :y= || (0<x <4)上存在两点,曲线C 在该两点处的切线相互垂直,则a 的取值范围是 .【答案】(0,)【解析】设曲线C 在点(x 1,f (x 1))和(x 2,f (x 2))处的切线相互垂直,不妨设x 1<x 2,则f’(x 1)f’(x 2)=-10<x <a 时,f(x)=-,f’(x)=<0;x>a 时,f(x)=,f’(x)=>0;∴ 0<a <4且0<x 1<a <x 2<4于是f’(x 1)=, f’(x)=;=-1化简得x 1+2a =, 又∵x 1+2a ∈(2a ,3a ),∈(,1)21x121ax ax 2+-21a x a x 2+-2)2(3a x a +-a x a x 2+-2)2(3a x a+21)2(3a x a +-22)2(3a x a +21)2(3a x a +-22)2(3a x a+a x a 232+ax a232+a a 243+∴(2a ,3a )∩(,1)≠Φ,即 解得 0<a <例5.4 设f(x)=x 2,g (x)=-(x -1)2,P 、Q 分别是曲线y=f(x)和y=g(x)上的动点,A(s,f(s))和B(t,g(t))分别是曲线上的定点,满足|AB |≤|PQ |对任意P 、Q 都成立. 下面四个数中,哪一个最接近s ? A.B. C. D. 【答案】B【解析】设f(x)、g(x)在A 、B 处的切线分别为l 、m ,则当l ∥m 且l ⊥AB 时|AB |取得最小值f’(x)=2x ,g’(x)= 2-2x ,所以:2s =2-2t ,且2s ×s 2+(t−1)2s−t=-1消去t 整理得:4s 3+2s -1=0,设h(s)= 4s 3+2s -1,易得h(s)为增函数 则h (0)<0,h (1)>0,h (12)>0,h (14)<0,h (38)<0所以s ∈(38,12),区间中点为716例5.5若x =-2是函数f(x)=(x 2+ax -1)e x -1的极值点,则f(x)的极小值为【答案】-1【解析】由f’(-2)=0可得a =-1,此时f ’(x)=(x +2)(x -1) e x -1 f(x)min =f (1)=-1例5.6 已知函数有两个极值点m 、n (m <n ),则 ( )A .f(m)<0,f(n)<-B .f(m)<0,f(n)>-C .f(m)>0,f(n)<-D .f(m)>0,f(n)>- 【答案】D【解析】由题意知 f ′(x )=ln x +1-2ax =0在区间(0,+∞)上有两个根.令h (x )=ln x +1-2ax ,则h ′(x )=xax21-, 当a ≤0时h ′(x )>0,f ′(x )在区间(0,+∞)上递增,f ′(x )=0不可能有两个正根,∴a >0.由h ′(x )=0,可得12x a =,因此111=ln +11=ln >0222h a a a ⎛⎫- ⎪⎝⎭,故10<<2a 且121<2x x a <.又h (1)=1-2a >0,∴1211<2x x a<<此时f (x )在区间(0,x 1)上递减,在区间(x 1,x 2)上递增,在区间(x 2,+∞)上递减. ∴f (x 1)<f (1)=-a <0,f (x 2)>f (1)=12a ->-. 故选D.例5.7设奇函数f(x)满足:f (-1)=0,当x >0时xf’(x)-f(x)<0,则使得f(x)>0成立的x 的范围是 . 【答案】(-1,0)∪(0,1) 【解析】f (0)=0不满足;令g(x)= f(x)x ,则g(x)为偶函数,且g’(x)=xf’(x)-f(x)x 2a 243+⎪⎩⎪⎨⎧<+>122433a a a a 211651671691611()(ln )f x x x ax =-21212121依题意x >0时g’(x)<0,故g(x)在(0,+∞)为减函数,在(-∞,0)为增函数 g (-1)=g (1)=0,所以-1<x <0或者0<x <1 【要点】构造函数,利用函数单调性解决不等式问题六、综合例题选讲(重要的代数方法及数学思想)【典型例题】例6.1 已知函数f(x)=x 2e 2x +m |x |e x +1有4个零点,则m 的取值范围是 【答案】(−e+1e 2,+∞) 【解析】令g(x)=|x |e x =|x e x |,令f 1(x )=x e x ,则f 1(x ) (-∞,-1)为为减函数,在(-1,+∞)为增函数 作出y=g(x)的图像,则直线y=t 与曲线y=g(x)的公共点的个数N :当t <0时N =0;当t =0时N =1;当1e<t <0时N=3;当t=1e时N=2;当t >1e时N=1考虑二次函数h(t)=t 2+mt +1,t =0不是零点, 故f(x)=x 2e 2x +m |x |e x +1有4个零点,当且仅当g(t) 在区间(0,1e)和(1e,+∞)各有1个零点,所以h (0)>0,h (1e)<0,解得 【要点】变量替换例6.2 设函数f (x )=a 1-x 2+1+x +1-x ,若总存在x 0∈[-1,1],使得f (x 0)>23,则a 的取值范围 是【答案】(-,+∞)【解析】设t=1+x +1-x ,t 2=2+2∈[2,4],t ∈[,2];此时f (x )=m(t)=t 2+t -a ,依题意:m(t)max >23 当a ≥0时, m(t)在[,2]上为增函数,m(t)max =m (2)=a +2 >23,符合题意 a <0时,m(t)的对称轴为t = 当<,即a <时,m(t)max =m ()=<23,不符题意当≤≤2,即≤a ≤-时,m(t)max ==m () =-a >23,无解当-<a <0时,m(t)max ==m (2)=a +2>23,符合题意,综上a >-【要点】变量替换例6.3 设f(x)=e x +e -x ,g(x)=f (2x )-2af(x)+4a -2,若g(x)恰有1个零点,则a 的取值范围是 【答案】[2,+∞) 【解析】由于(f(x))2= e 2x +e-2x+2,g(x)= e 2x +e-2x-2a (e x +e -x )+ 4a -2=(e x +e -x )2-2a (e x +e -x ) +4a -4=(f(x))2-2af(x)+ 4a -4=[f(x)-2][f(x)-(2a -2)]2121x -∴22a 2a1-a 1-222-222a 1-22-21a 1-a 21-2121由于f(x)-2=0恰有1个根x =0,所以f(x)-(2a -2)=0无根或只有1个0根 由于f(x)值域为[2,+∞),所以(2a -2)≤2,解得答案 【要点】变量替换、因式分解例6.4 设a >0,函数f(x)=23x 2-2ax -a 2ln x -b ,若f(x)恰有1个零点,则b 的最大值为 【答案】12e 2【解析】f’(x)=(3x+a)(x−a)x(x >0),f(x)在(0,a )减,(a ,+∞)增依题意:f(a)=0解得b =-a 2-a 2ln a (记为g(a)) g’(a)=-2a (1+ln a ),g(a)在(0,1e)为增,( 1e,+∞)为减,所以b max =g (1e)= 12e 2【要点】等价转化例6.5 已知函数f(x)=e x -ax 2+bx -1 满足f (1)=0,且f(x)在区间(0,1)内有零点,则a 的取值范围是 【答案】(e -1,1)【解析】注意到f (0)=f (1)=0,依题意f(x)在(0,1)内至少有2个极值点,即f’(x)在(0,1)内至少有2个零点 由f (1)=e -a +b -1=0,可得b =1-e +a f’(x)= e x -2ax +b ,(f’(x))’=e x -2a ,由e>e x >1若a ≤12,则(f’(x))’ >0,f’(x)为增函数,不会有2个零点,不符题意; 若a ≥e 2,同理不符题意当 12<a <e 2 时,f’(x)在(0,ln2a )为减函数,(ln2a ,1)为增函数f’(x)在(0,1)内有2个零点,充要条件为:{f ′(0)>0f ′(ln2a )<0f ′(1)>0解得:e -1<a <1 【要点】等价转化例6.6 若函数f (x )=(1-x 2)(x 2+ax +b )的图像关于直线x =-2对称,则f (x )的最大值为__________. 【答案】16【解法一】由f (1)=f (-1)=0,f(x)图像关于x =-2对称,所以f (-5)=f (-3)=0 故a =-(-3-5)=8,b =15此时f (x )=-(x +1)(x -1)(x +3)(x +5)=-(x 2+4x +3)(x 2+4x -5) =-(t 2-2t -15)=-(t -1)2+16其中:t = x 2+4x ∈[-4,+∞),当t= 1时f(x)max =16【解法二】考虑g(x)=f (x -2)为偶函数,g (-1)=g (-3)=0,所以g (1)=g (3)=0 故g(x)=-(x +3)(x +1)(x -1)(x -3)=-(x 2-1) (x 2-9)=-(x 2-5)2+16 【要点】(1) 变量替换(2) 灵活处理对称条件21例6.7 设f(x)=e x -x -e +1,命题p :f(x)≤0,命题q :-1≤x ≤1,则p 是q 的: A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件 【答案】C【解析】注意到f (1)=0,f’(x)= e x -1,所以f(x)在(-∞,0)为减,(0,+∞)为增f (-1)=2+e -1-e<0,f (-2)=3+e -2-e>0,所以f(x)在(-∞,0)上有一个零点,设为x 0, f(x)≤0的充要条件为x 0≤x ≤1由于-2<x 0<-1,故为-1≤x ≤1的必要不充分条件 【要点】单调性与不等式例6.8 设f(x)=e x -ax -1,g(x)=ln x -ax+a ,若总存在x ∈(1,2),使得f(x)g(x)<0,则a 的取值范围 是 【答案】[ln2,e 2−12]【解析】f’(x)= e x -a ,g’(x)= 1x-a ,注意到e x ∈(e ,e 2),1x∈( 12,1),故对a 分类讨论(1) 当a ≤12时,f’(x)≥0,g’(x)≥0,故f(x)、g(x)都是(1,2)上的增函数,f(x)>f (1)= e -a -1>0,g(x)>g (1)=0,故不符题意;(2) 当12<a ≤1时,同理f(x)> 0,而g(x)在(1,1a)为增,( 1a ,2)为减依题意:g (2) ≤0,解得ln2≤a ≤1(3) 1<a ≤e 时:g(x)是(1,2)上的减函数,所以g(x)<g (1)=0f(x)是(1,2)上的增函数,故f(2)≥0,解得1<a ≤e(4) e<a ≤e 2时:同理g(x)<0,此时f(x)在(1,ln a )为减,(ln a ,2)为增,故f(1)≥0或者f(2)≥0解得e<a ≤e 2−12(5) a ≥e 2时:f(x)是(1,2)上的减函数,f(x)<f (1)= e -a -1<0,同理g(x)<0,不符题意【要点】分类讨论例6.9 设f(x)=2ax 2+(a -1)x -1 (a >0),求函数y =|f(x)|在[-1,1]上的最大值【分析】结合|f(x)|的图像,判定f(x)的零点与定义域的位置关系,再比较极值与端点函数值的大小【解析】 由a >0,f (0)=-1<0, f (-1)=a >0,所以:f(x)有两个零点(设为x 1x 2)满足:x 1<-1<x 2 f(x)的对称轴为x 0=a a 41-,t 0-1=aa451- 情形①:当0<a ≤51时,1≤x 0,| f(x)|在(-1,x 1)减,(x 1, 1)增x 2x 0-1x 1而|f (1)|= 2-3a >|f (-1)|,所以:|f(x)|max =2-3a情形②:51<a <32时,x 0<x 2<1, |f(x)|在 (-1,x 1)减,(x 1, x 0)增,(x 1, x 2)减,(x 2,1)增|f(x)|max =max{|f(-1)|,|f(x 0)|,|f(1)|}|f (1)|-|f (-1)|=2(a -1)<0|f (x 0)|=a a a 8162++ |f (x 0)|-|f (-1)|=a a a 8)1)(17(-+->0所以:|f(x)|max =aa a 8162++情形③:a 32≥时, x 0<1≤x 2, |f(x)| 在(-1,x 1)减,(x 1,x 0)增,(x 0,1)减 |f(x)|max =max{|f(-1)|,|f(x 0)| } 故当 a <1时:|f(x)|max =aa a 8162++当a ≥1时:|f(x)|max =|g (1)|=3a -2综上,|f(x)|max ={2−3a ,0<a ≤15a 2+6a+18a, 15<a <13a −2, a ≥1.【要点】分类讨论。

专题二函数概念与基本初等函数Ⅰ第六讲函数综合及其应用答案部分x1.A【解析】解法一函数f (x) 的图象如图所示,当y | a |的图象经过点(0, 2) 时,可2y x a 的图象与y x 2 的图象相切时,由 2x 知a 2 .当 a x ,得2 x 2 xx x 2 2ax 4 0 ,由0,并结合图象可得a 2 ,要使f (x)≥| a |恒成立,当2a ≤时,需满足 a ≤2 ,即2≤a ≤0 ,当a 0 时,需满足a ≤2 ,所以2≤a ≤2.y654321–4–3–2O 1 2 3 4–1–1xx 解法二由题意x 0 时,f (x) 的最小值2,所以不等式f (x)≥| a |等价于2x| a |≤2 在R上恒成立.2x ,不符合题意,排除C、D;当a 2 3 时,令x 0 ,得| 2 3 | 22x ,不符合题意,排除B;当a 2 3 时,令x 0 ,得| 2 3 | 22选A.2.B【解析】由f (x ) f (2 x)知f (x)的图像关于直线x 1对称,又函数y | x 2 2x 3||(x 1)2 4 | 的图像也关于直线x 1对称,所以这两个函数图像的交点也关于直线x 1对称,不妨设x xx x x ,则 1 1,即x x ,1 m 2m1 2 m2,m同理x 2 x m 1 2 ,……,由Array x x x xi 1 2 mi11m2 x (x x ) (x x ) (x x ) 2mi 1 m 2 m 1 m 1所以i1,所以mx mii1,故选B.3.B【解析】由已知可设f(x)2 ( 0)xxx2( 0)x,则f(a)2 (a0)a2a( 0)a,因为f(x) 为偶函数,所以只考虑a 0 的情况即可.若f(a ) 2b,则2a 2b,所以a b.故选B.4.B【解析】因为第一次邮箱加满,所以第二次的加油量即为该段时间内的耗油量,故耗油量V 48 升.而这段时间内行驶的里程数S 35600 35000 600 千米.所以这段时间内,该车每100 千米平均耗油量为48100 8 升,故选B.6005.B 【解析】采用特殊值法,若x 1, y 2, z 3,a 1,b 2,c 3,则ax by cz 14 ,az by cx 10 ,ay bz cx 11,ay bx cz 13 ,由此可知最低的总费用是az by cx .6.B【解析】由题意可知p at 2 bt c过点(3,0.7),(4,0.8)(5,0.5),代入p at 2 bt c中可解得a 0.2,b 1.5,c 2 ,∴p 0.2t 2 1.5t 2 0.2(t 3.75)2 0.8125∴当t 3.75分钟时,可食用率最大.7.D【解析】设年平均增长率为x ,原生产总值为a ,则(1p )(1q)a a (1x)2 ,解得x (1p )(1q ) 1,故选D.8.A【解析】解法一由题意可知,该三次函数满足以下条件:过点(0,0),(2,0),在(0,0)处的切线方程为y= -x,在(2,0)处的切线方程为y= 3x-6,以此对选项进行检验.A选项,y 1 x 3 1 x 2 x ,显然过两个定点,又 3 2 1y x x ,2 2 2则y y ,故条件都满足,由选择题的特点知应选A.| 1, | 3x 0 x 2解法二设该三次函数为f (x) ax3 bx2 cx d ,则f (x) 3ax2 2bx c2f (0)f (2) 0由题设有,解得f (0) 1f (2) 31 1a ,b ,c 1,d 0 .2 2故该函数的解析式为 1 3 1 2y x x x ,选A.2 29.A【解析】设所求函数解析式为y f (x) ,由题意知f (5) 2, (f 5)2,且f (5) 0,代入验证易得 1 3 3y x x 符合题意,故选A.125 5110.[ , 2]【解析】当3≤x≤0 时,f (x)≤| x | 恒成立等价于x 2 2x a 2≤x 恒成8立,即a ≤x 2 3x 2 恒成立,所以a ≤(x 3x 2) 2;2min当x 0 时f (x)≤| x | 恒成立等价于x 2 2x 2a ≤x 恒成立,即x x x x 1 22a≥恒成立,所以a≥( ) .max2 2 8综上,a 的取值范围是[1 ,2].811.36【解析】取SC 的中点O ,连接OA,OB ,因为SA AC,SB BC ,所以OA SC,OB SC .因为平面SAC 平面SBC ,所以OA 平面SBC .设OA r ,1 1 1 1V S OA r r r r23A SBC SBC3 3 2 3所以1 3 9 3r r ,3所以球的表面积为4r 2 36.1【解析】由题意,u x2 y2 x2 (1x)2 2x2 2x 1,且x[0,1],12.[ ,1]2x 时, 2 2 11又x 0 时,u x2 y2 1,u x y ,当x 1时,u x2 y2 1,2 21所以x2 y2 取值范围为[ ,1].21 113.7 【解析】由体积相等得:452 +22 8= r2 4 r2 8 r 7 .3 3314.(2 10,) 【解析】函数g(x) 的定义域为[1, 2] ,h x g x( ) ( )根据已知得f x2,所以h(x)=2 f (x ) g(x ) 6x 2b 4 x2 ,h(x ) g(x) 恒成立,即6x 2b 4 x 2 4 x2 ,令y 3x b ,y 4 x2 ,则只要直线y 3x b在半圆x 2 y 2 4(y≥0) 上方即可,由| b | 2,解得b 2 10(舍去负值),故实10数b 的取值范围是(2 10,) .15.160【解析】设该容器的总造价为y 元,长方体的底面矩形的长x m ,因为无盖长方体的容积为4m3 ,高为1m,所以长方体的底面矩形的宽为4xm ,依题意,得2 4 4 4y 20 4 10(2x ) 80 20(x )≥8020 2 x 160.x x x16.①③④【解析】对于①,根据题中定义,f (x) A 函数y f (x) ,x D 的值域为R ,由函数值域的概念知,函数y f (x) ,x D 的值域为R b R ,a Df a b ,所以①正确;对于②,例如函数( ) (1)| |( ) f x 的值域(0,1]包含于区间[1,1],x2所以f (x)B,但f (x) 有最大值l,没有最小值,所以②错误;对于③,若f (x ) g(x) B ,则存在一个正数M,使得函数f (x ) g(x) B 的值域包含于区1间[M ,M ] ,所以M ≤f (x)1 1 1g(x)≤M ,由g(x)B知,存在一个正数M ,1 2使得函数g(x) 的值域包含于区间M2 g(x) M 2[M ,M ],所以≤≤,亦有2 2M2 ≤-g(x)≤M2 ,两式相加得(M M ) ≤f (x) ≤M M ,于是f (x) B ,1 2 1 2与已知“. f (x)A”矛盾,故f (x ) g(x ) B ,即③正确;对于④,如果a 0 ,那么x , f (x ) ,如果a 0 ,那么x 2, f (x ) ,所以f (x) 有最大值,必须a 0 ,此时 f (x )x 在区间(2,)上,有 1 ( ) 1≤f x ≤,所以x 2 2 21f (x)B,即④正确,故填①③④.417.【解析】(1)当0 x≤30 时,f (x ) 30 40恒成立,公交群体的人均通勤时间不可能少于自驾群体的人均通勤时间;当30 x 100 时,若40 f (x) ,即2x 1800 90 40,解得x 20(舍)或x 45 ;x∴当45 x 100 时,公交群体的人均通勤时间少于自驾群体的人均通勤时间;(2)设该地上班族总人数为n ,则自驾人数为n x% ,乘公交人数为n (1x%) .因此人均通勤时间30n x % 40n (1x%), 0 x≤30ng x( ) 1800,(2x 90)n x % 40n (1x %)x x,30 100n整理得:g(x)x40 , 0 x≤30101(x 32.5) 36.875,30 x 100250,则当x(0, 30]U(30,32.5],即x(0,32.5] 时,g(x) 单调递减;当x(32.5,100) 时,g(x) 单调递增.实际意义:当有32.5%的上班族采用自驾方式时,上班族整体的人均通勤时间最短.适当的增加自驾比例,可以充分的利用道路交通,实现整体效率提升;但自驾人数过多,则容易导致交通拥堵,使得整体效率下降.18.【解析】(1)由题意知,点M ,N 的坐标分别为5, 40,20, 2.5.将其分别代入yax b2a40a1000.25b,得,解得a b 02.5400 b(2)①由(1)知, y1000 1000( 5 x 20 ),则点 的坐标为 t ,,xt22设在点 处的切线l 交 x , y 轴分别于 A , B 点,2000,yx310002000则 l 的方程为 yx t,由此得tt23Α 3t ,0 2 , 3000Β 0,t2. 53t30003 4 10226f tt2故22t2t24,t 5, 20.410616106②设,则.令 g t0,解得t 10 2 .g ttg t 2t2tt45当t 5,10 2时, g t 0 , g t 是减函数;当t10 2, 20时,g t 0, g t是增函数.从而,当t 10 2 时,函数 g t有极小值,也是最小值,所以g t min 300 ,f t min 15 3 . 此时答:当t 10 2 时,公路l 的长度最短,最短长度为15 3 千米.19.【解析】(Ⅰ)因为蓄水池侧面积的总成本为1002rh 200rh 元,底面的总成本为160r 元,所以蓄水池的总成本为( 200rh 160r 2 )元.2又题意据 200rh 160r 2 12000 ,所以1 (300 42 )h r , 5r从而V (r ) r 2h (300r 4r 3 ).因 r 0 ,又由 h 0 可得 r 5 3 ,5故函数V (r ) 的定义域为 (0, 5 3) .(Ⅱ)因 ( )(300 4 3 ) .令V (r ) 0,V r r r ,故V (r ) (300 12r 2 )5 5解得 r r (因r r (因 1 5, 2 5r 不在定义域内,舍去).2 5 当 r (0,5)时,V (r ) 0,故V (r ) 在 (0, 5) 上为增函数;当r (5, 53) 时,V(r) 0 ,故V (r) 在(5, 5 3) 上为减函数.由此可知,V (r) 在r 5 处取得最大值,此时h 8.即当r 5 ,h 8时,该蓄水池的体积最大.20.【解析】(1)当b 1,c 1,n …2时,f (x) x n x 1.∵内存在零点.f f ,∴f (x) 在(1 ,1)( ) (1) ( ) 1 01 1 12 2n 2 2又当上是单调递增的,x时,f (x) nx n1 10,∴f (x) 在(1 ,1)( ,1)12 261∴f (x) 在区间( ,1)2内存在唯一的零点;(2)解法一由题意知剟f1 ( 1) 1,1剟f (1) 1,即0剟2,b c2剟b c0,由图像知,b 3c 在点(0,2) 取得最小值6 ,在点(0, 0) 取得最大值0 .cbO-2解法二由题意知1剟f (1) 1 b c 1,即2剟b c 0 .…①1剟f (1) 1b c 1,即2?-b c ?0.…②① 2 +②得6?2(-b c ) (b c ) b 3c ?0,当b 0,c 2 时,b 3c 6 ;当b c 0 时,b 3c 0 .所以b 3c 的最小值6,最大值0 .f (1) 1b c,解法三由题意知,f (1) 1 b c,f (1) f (1) f (1) f (1) 2解得b ,c ,2 2b 3c 2 f (1) f (1) 3.又∵剟1 f ( 1) 1,,∴6?b 3c ?0 .1剟f (1) 1,当b 0,c 2 时,b 3c 6 ;当b c 0 时,b 3c 0 .所以b 3c 的最小值6,最大值0 .(3)当n 2 时, f (x) x2 bx c .对任意x x [1,1]都有有1, 2f(x ) f (x ) …4 等价于f (x) 在[-1,1]上的最大值与最1 2小值之差M …4.据此分类讨论如下:7b ,即b 2时, M f (1) f (1) 2 b 4 ,与题设矛盾.(ⅰ)当 12b b b(ⅱ)当1…0,即0 b …2时, M f (1) f () ( 1)2 …4 恒成立.2 2 2b b b(ⅲ) 当0…1,即2剟b 0 时, M f (1) f () ( 1)2 …4 恒成立.2 2 2综上可知, 2剟b 2 .21.【解析】设包装盒的高为h (cm),底面边长为a (cm),由已知得a 2x h 60 2x x x, 2(30 ),0230.(1)S 4ah 8x (30 x ) 8(x 15)2 1800 ,所以当x 15 时,S 取得最大值.(2)V a2h 2 2 (x 2 30x2 ),V 6 2x (20 x). 由V 0得x 0(舍)或x =20.当x (0,20) 时,V 0 ;当x(20,30)时V 0 .所以当x =20 时,V 取得极大值,也是最小值.此时ha1,即装盒的高与底面边长的比值为212.8。

训练目标 (1)函数单调性的概念;(2)函数的最值及其几何意义. 训练题型 (1)判断函数的单调性;(2)利用函数单调性比较大小、解不等式;(3)利用函数单调性求最值.解题策略(1)判断函数单调性常用方法:定义法、图象法、导数法、复合函数法;(2)分段函数单调性要注意分界点处函数值的大小;(3)可利用图象直观研究函数单调性. 2.已知f (x )是定义在区间[-1,1]上的增函数,且f (x -2)<f (1-x ),则x 的取值范围是________.3.函数f (x )=11-x (1-x )的最大值是________. 4.已知函数f (x )=⎩⎪⎨⎪⎧-x 2-ax -5,x ≤1,a x,x >1在R 上为增函数,则a 的取值范围是________. 5.函数f (x )=x 2-4x +5在区间[0,m ]上的最大值为5,最小值为1,则m 的取值范围是________.6.函数f (x )=|log 3x |在区间[a ,b ]上的值域为[0,1],则b -a 的最小值为________.7.若存在正数x 使2x (x -a )<1成立,则a 的取值范围是________.8.(2015·上海黄浦区期中调研测试)若函数f (x )=2x 2+ax +1-3a 是定义域为R 的偶函数,则函数f (x )的单调递减区间是________.9.设函数f (x )=x 2+(a -2)x -1在区间(-∞,2]上是减函数,则实数a 的最大值为________.10.若定义在R 上的二次函数f (x )=ax 2-4ax +b 在区间[0,2]上是增函数,且f (m )≥f (0),则实数m 的取值范围是________.11.(2015·洛阳二模)函数y =f (x )(x ∈R )的图象如图所示,则函数g (x )=f (log a x )(0<a <1)的单调减区间是________.12.已知函数f (x )是定义在R 上的偶函数,且在区间[0,+∞)上单调递增.若实数a 满足f (log 2a )+f (log 12a )≤2f (1),则a 的取值范围是________. 13.(2015·广东深圳五校联考)已知函数f (x )=-x 3-x +sin x ,当θ∈(0,π2)时,恒有f (cos 2θ+2m sin θ)+f (-2m -2)>0成立,则实数m 的取值范围是________.14.(2015·昆明模拟)已知函数f (x )的图象向左平移1个单位后关于y 轴对称,当x 2>x 1>1时,[f (x 2)-f (x 1)]·(x 2-x 1)<0恒成立,设a =f (-12),b =f (2),c =f (3),则a ,b ,c 的大小关系为________.(用“>”连接)答案解析1.(-∞,1]∪[2,+∞)解析 二次函数在某区间内是否单调取决于对称轴的位置,函数f (x )=x 2-2mx -3的对称轴为x =m ,函数在区间[1,2]上单调,则m ≤1或m ≥2.2.[1,32) 解析 由题意,得⎩⎪⎨⎪⎧ -1≤x -2≤1,-1≤1-x ≤1,x -2<1-x ,解得1≤x <32,故满足条件的x 的取值范围是1≤x <32. 3.43解析 因为f (x )=1(x -12)2+34,所以当x =12时,f (x )取得最大值43. 4.[-3,-2]解析 要使函数在R 上是增函数则有⎩⎪⎨⎪⎧ -a 2≥1,a <0,-1-a -5≤a ,解得-3≤a ≤-2.5.[2,4] 解析 由f (x )=(x -2)2+1知,当x =2时,f (x )的最小值为1,当f (x )=5,即x 2-4x +5=5时,解得x =0或x =4.依据图象(图略),得2≤m ≤4.6.23解析 令f (x )=0,得x =1;令f (x )=1,得x =13或3. 因为f (x )在(0,1)上为减函数,在(1,+∞)上为增函数,故b -a 的最小值为1-13=23. 7.(-1,+∞)解析 由题意知,存在正数x ,使a >x -12x ,所以a >(x -12x )min ,而函数f (x )=x -12x 在(0,+∞)上是增函数,所以f (x )>f (0)=-1,所以a >-1.8.(-∞,0]解析 由已知得a =0,从而f (x )=2x 2+1,由复合函数的单调性可知函数f (x )的单调递减区间是(-∞,0].9.-2解析 函数f (x )的图象的对称轴为直线x =-a -22,则函数f (x )在(-∞,-a -22)上单调递减,在区间[-a -22,+∞)上单调递增,所以2≤-a -22,解得a ≤-2. 10.0≤m ≤4解析 由于f (x )在区间[0,2]上是增函数,所以f (2)>f (0),解得a <0.又因为f (x )图象的对称轴为x =--4a 2a=2.所以x 在[0,2]上的值域与在[2,4]上的值域相同,所以满足f (m )≥f (0)的m 的取值范围是0≤m ≤4.11.[a ,1]解析 由图象可知,函数y =f (x )的单调递减区间为(-∞,0)和(12,+∞), 单调递增区间为[0,12]. ∵0<a <1,∴函数y =log a x 在定义域内单调递减.由题意可知,0≤log a x ≤12,解得a ≤x ≤1,即所求递减区间为[a ,1].12.⎣⎡⎦⎤12,2解析 由题意知a >0,又log 12a =log 2a -1=-log 2a . ∵f (x )是R 上的偶函数,∴f (log 2a )=f (-log 2a )=f (log 12a ). ∵f (log 2a )+f (log 12a )≤2f (1), ∴2f (log 2a )≤2f (1),即f (log 2a )≤f (1).又因f (x )在[0,+∞)上递增,∴|log 2a |≤1,-1≤log 2a ≤1,∴a ∈⎣⎡⎦⎤12,2.13.[-12,+∞) 解析 因为函数f (x )=-x 3-x +sin x 是奇函数且f ′(x )=-3x 2-1+cos x ≤0,所以函数f (x )=-x 3-x +sin x 在R 上是减函数.不等式f (cos 2θ+2m sin θ)+f (-2m -2)>0等价于f (cos 2θ+2m sin θ)>-f (-2m -2)=f (2m +2)⇔cos 2θ+2m sin θ<2m +2⇔2m (1-sin θ)>cos 2θ-2⇔m >cos 2θ-22(1-sin θ)=sin 2θ+12(sin θ-1),θ∈(0,π2). 记g (θ)=sin 2θ+12(sin θ-1),令sin θ=t ∈(0,1), 则g (t )=t 2+12(t -1),g ′(t )=2t (t -1)-(t 2+1)2(t -1)2=t 2-2t -12(t -1)2=(t -1)2-22(t -1)2<0在t ∈(0,1)上恒成立,所以函数g (t )=t 2+12(t -1)在t ∈(0,1)上是减函数,从而g (θ)=sin 2θ+12×(sin θ-1)<02+12×(0-1)=-12在(0,π2)上恒成立,所以实数m 的取值范围为[-12,+∞). 14.b >a >c解析 根据已知可得函数f (x )的图象关于直线x =1对称,且在(1,+∞)上是减函数.因为a=f (-12)=f (52),且2<52<3,所以b >a >c .。

专题二函数概念与基本初等函数Ⅰ第六讲函数综合及其应用答案部分1.A【解析】解法一根据题意,作出f (x) 的大致图象,如图所示yy=f(x)O 1x当x ≤1时,若要 f (x) ≥|x+a | 恒成立,结合图象,只需x 2 -x +3≥-(x+a) ,即2x 2 -x+3 +a ≥0,故对于方程x 2 -x+3 +a =0 ,∆=(-1)2 -4(3+a)≤0,解得2a ≥-47;当x >1 时,若要f (x)≥|x+a | 恒成立,结合图象,只需x +2≥x+a ,2 2 216 2x 2即+≥a,又+≥2 ,当且仅当=,即x = 2 时等号成立,所以a ≤2 ,2 x 2 x 2 xx 2 x 2 x 2综上,a 的取值范围是[-47, 2] .选A.16解法二由题意f (x) 的最小值为11,此时x =1.不等式f (x) ≥|x+a | 在R 上恒成立等价于| x+a |≤11在R 上恒成立.422 2 4当a =-2 3 时,令x =1,|x-2 3 |=|8 3 -1|>11,不符合,排除C、D;2 2 48当a =39时,令x =1,|x+39|=|43|>11,不符合,排除B.选A.16 2 2 16 16 82.D【解析】“燃油效率”是指汽车每消耗1 升汽油行驶的里程,A 中乙车消耗1 升汽油,最多行驶的路程为乙车图象最高点的纵坐标值,A 错误;B 中以相同速度行驶相同路程,甲燃油效率最高,所以甲最省油,B 错误,C 中甲车以80 千米/小时的速度行驶1 小时,甲车每消耗1 升汽油行驶的里程10km,行驶80km,消耗8 升汽油,C 错误,D 中某城市机动车最高限速80 千米/小时.由于丙比乙的燃油效率高,相同条件下,在该市用pq丙车比用乙车更省油,选 D .3.B 【解析】由题意可知 p = at 2 + bt + c 过点(3,0.7),(4,0.8)(5,0.5),代入p = at 2 + bt + c 中可解得a = -0.2,b = 1.5, c = -2 ,∴ p = -0.2t 2 +1.5t - 2 =-0.2(t - 3.75)2 + 0.8125 ,∴当t = 3.75 分钟时,可食用率最大.4.D 【解析】设年平均增长率为 x ,原生产总值为a ,则(1+ p )(1+ q )a = a (1+ x ) 2,解得x = (1+ p )(1+ q ) -1 ,故选 D .5.①④【解析】①e xf (x ) = e x⋅2-x= ( e )x 在R 上单调递增,故 f (x ) = 2- x具有M 性质; 2② e x f (x ) = e x ⋅3 -x = ( e)x 在R 上单调递减,故 f (x ) = 3- x不具有M 性质;3③ e x f (x ) = e x ⋅ x 3,令 g (x ) = e x ⋅ x 3,则 g '( x ) = e x ⋅ x 3+ e x ⋅ 3x 2= x 2e x( x + 2) ,∴当 x > -2时, g '(x ) >0 ,当 x < -2时, g ' (x )< 0 ,∴ e x f (x ) = e x ⋅ x 3 在(-∞, -2) 上单调递减,在(-2, +∞) 上单调递增,故 f (x ) = x 3 不具有M 性质;④e xf (x ) = e x(x 2 + 2),令 g (x ) = e x (x 2 + 2), 则 g '(x ) = e x (x 2 + 2) + e x ⋅ 2x = e x [(x + 1)2+ 1]> 0 ,∴ e x f (x ) = e x (x 2 + 2) 在R 上单调递增,故 f (x ) = x 2 + 2具有M 性质.6.8【解析】由于 f (x ) ∈[0,1) ,则需考虑1≤ x <10 的情况,在此范围内, x ∈Q 且 x ∈ D 时,设x = q , p , q ∈ N * , p ≥ 2 ,且 p , q 互质, 若lg x ∈Q ,则由lg x ∈(0,1) ,可设lg x =n, m , n ∈ N *, m ≥ 2 ,且m , n 互质, mn 10 = 10n = ( q )m因此m,则pp,此时左边为整数,右边为非整数,矛盾,因此lg x ∉Q ,因此lg x 不可能与每个周期内 x ∈ D 对应的部分相等,只需考虑lg x 与每个周期 x ∉ D 的部分的交点,画出函数图象,图中交点除外(1, 0) 其他交点横坐标均为无理数,属于每个周期 x ∉ D 的部分,且 x =1处(lg x )' =1=1< 1 ,则在 x =1 附近仅有一个交点,x ln10 ln10因此方程 f (x ) - lg x = 0 的解的个数为 8.7. 4 15 【解析】如图连接OE 交 AC 于G ,由题意OE ⊥ AC ,设等边三角形ABC 的边长为 x (0 < x < 5 ),则OG = 3 x ,GE = 5- 6 3 x . 6EAGFO CBD由题意可知三棱锥的高h =GE 2 - OG 2=(5-3 x )2 - (3 x )2 = 25-5 3 x底面 S∆ABC =3 x 2, 4663三棱锥的体积为V = 1⨯3 x 2⨯ 25- 5 3 x = 15 5x4 - 3 x5 , 34 3 12 3设h (x ) = 5x 4 -3 x 5 ,则h '(x ) = 20x 3 - 5 3 x 4(0 < x < 5 ), 3 3令 h '(x ) = 0 ,解得x = 4 3 ,当x ∈(0, 4 3) 时, h '(x ) > 0 ,h (x ) 单调递增; 当 x ∈(4 3,5) 时,h '(x ) < 0 , h (x ) 单调递减,⎩所以 x = 4 3 是h (x ) 取得最大值h (4 3) = (4 3)4所以V = 15 ⨯ h (4 3) = 15⨯ (4 3)2 = 4 15. max812 12⎧ x 3- 3x ,x ≤ 0 . 2 ,(-∞, -1) .【解析】①若 a = 0 ,则 f (x ) = ⎨ -2x , x > 0,当 x > 0 时,-2x < 0 ;当 x … 0 时, f '( x ) = 3x 2 - 3 = 3( x + 1)(x - 1) ,所以函数 f ( x ) 在(-∞, -1) 上单调递增,在(-1, 0] 上单调递减,所以函数 f ( x )在(-∞, 0] 上的最大值为 f (-1) = 2 .综上函数 f (x ) 的最大值为 2.②函数 y = x 3- 3x 与 y = -2x 的大致图象如图所示y 321–2 –1 O–1–2123若 f (x ) 无最大值,由图象可知-2a > 2 ,即a < -1.⎧ e b= 192 9.24【解析】由题意得⎨ e 22k +b = 48 ⎧e b =192 ⎪⎨e 11 k = 1 ,所以该食品在33 ℃的保鲜时间是 ⎪⎩ 2y = e 33k +b = (e 11k )3 ⋅ e b = (1)3⨯ 193= 24 .210.(2 10, +∞)【解析】函数 g (x ) 的定义域为[-1, 2] ,根据已知得h ( x ) + g ( x )= f (x ) ,2所以 h (x )=2 f (x ) - g (x ) = 6x + 2b - 4 - x 2 , h (x ) > g (x ) 恒成立,即6x + 2b - 4 - x 2 > 4 - x 2 ,令 y = 3x + b ,y = 4 - x 2 ,则只要直线y = 3x + b在半圆 x 2 + y 2= 4( y ≥0) 上方即可,由 | b |10> 2,解得b > 2 10 (舍去负值),故实数b 的取值范围是(2 10, +∞) .⎩ ,即11.160【解析】设该容器的总造价为y 元,长方体的底面矩形的长x m ,因为无盖长方体的容积为4m 3 ,高为1m ,所以长方体的底面矩形的宽为4m ,依题意,得xy = 20⨯ 4+ 10(2x + 2⨯4) = 80+ 20(x + 4)≥ 80+ 20⨯ 2 x ⋅ 4= 160x x x12.①③④【解析】对于①,根据题中定义, f (x )∈ A ⇔ 函数 y = f (x ) , x ∈ D 的值域为R ,由函数值域的概念知,函数 y = f (x ) , x ∈ D 的值域为R ⇔ ∀b ∈ R ,∃a ∈ Df (a ) = b ,所以①正确;对于②,例如函数 f (x ) = ( 1)|x | 的值域(0,1] 包含于区间[-1,1] ,2所以 f (x ) ∈ B ,但 f (x ) 有最大值 l ,没有最小值,所以②错误;对于③,若f (x ) +g (x )∈ B ,则存在一个正数 M 1 ,使得函数 f (x ) + g (x )∈ B 的值域包含于区间[-M 1, M 1] ,所以-M 1 ≤ f (x ) +g (x ) ≤ M 1 ,由 g (x ) ∈ B 知,存在一个正数M 2 ,使得函数 g (x ) 的值域包含于区间[-M 2 , M 2 ],所以-M 2 ≤ g (x ) ≤ M 2 ,亦有-M 2 ≤ -g (x ) ≤ M 2 ,两式相加得 -(M 1 + M 2 ) ≤ f (x ) ≤M 1 + M 2 ,于是 f (x ) ∈ B ,与已知“. f (x ) ∈ A ”矛盾,故 f (x ) + g (x ) ∉ B ,即③正确;对于④,如果a > 0 , 那么 x → +∞, f (x ) → +∞ ,如果a < 0 ,那么 x → -2, f (x ) → +∞ ,所以 f (x ) 有最大值,必须a = 0 ,此时 f (x ) = x x 2+1 在区间(-2, +∞) 上,有- 1 ≤ f (x )≤ 1 ,2 2所以 f (x ) ∈ B ,即④正确,故填①③④.13.【解析】(1)当0 < x ≤30 时, f (x ) = 30 < 40 恒成立,公交群体的人均通勤时间不可能少于自驾群体的人均通勤时间; 当30 < x <100 时,若40 < f ( x ) ,即 2x + 1800 - 90 > 40 ,解得x < 20(舍)或x > 45 ;x∴当45 < x <100 时,公交群体的人均通勤时间少于自驾群体的人均通勤时间; (2)设该地上班族总人数为n ,则自驾人数为n ⋅ x % ,乘公交人数为n ⋅ (1- x %) .⎨ x n B⎧ 30 ⋅ n ⋅ x % + 40 ⋅ n ⋅(1 - x %) ,0 < x ≤30n 因此人均通勤时间 g (x ) = ⎪ , ⎨ (2x + 1800 - 90)⋅ n ⋅ x % + 40⋅ n ⋅ (1- x %) ⎪⎪, 30 < x < 100 ⎩⎧40 - 整理得: g (x ) = ⎪ 1 x, 0 < x ≤ 30 10 , 2⎪ ⎪⎩50(x - 32.5) + 36.875, 30 < x < 100则当 x ∈ (0, 30] (30, 32.5],即 x ∈ (0, 32.5] 时, g (x ) 单调递减; 当x ∈(32.5,100) 时, g (x ) 单调递增.实际意义:当有32.5% 的上班族采用自驾方式时,上班族整体的人均通勤时间最短. 适当的增加自驾比例,可以充分的利用道路交通,实现整体效率提升;但自驾人数过多, 则容易导致交通拥堵,使得整体效率下降.14.【解析】(1)连结PO 并延长交MN 于 H ,则PH ⊥ MN ,所以OH =10.PDCG θE KM AO HN过O 作OE ⊥ BC 于 E ,则OE ∥ MN ,所以∠COE =θ, 故OE = 40cos θ, EC = 40sin θ,则矩形 ABCD 的面积为2⨯ 40cos θ(40sin θ+10) = 800(4sin θcos θ+ cos θ) ,∆CDP 的面积为1⨯ 2 ⨯ 40 cos θ(40 - 40 sin θ) =1600(cos θ-sin θcos θ) .2过N 作GN ⊥ MN ,分别交圆弧和OE 的延长线于G 和 K ,则GK = KN = 10 .令∠GOK =θ ,则sin θ = 1 ,θ ∈ (0,π) .0 04 0 6当θ∈[θ ,π) 时,才能作出满足条件的矩形 ABCD ,0 2所以sin θ的取值范围是[ 1,1) .4答:矩形 ABCD 的面积为800(4sin θcos θ+ cos θ)平方米, ∆CDP 的面积为1600(cos θ- sin θcos θ) , sin θ的取值范围是[ 1,1).4(2)因为甲、乙两种蔬菜的单位面积年产值之比为 4∶3,设甲的单位面积的年产值为4k ,乙的单位面积的年产值为3k (k > 0) ,则年总产值为4k ⨯800(4sin θcos θ+cos θ) +3k ⨯1600(cos θ-sin θcos θ)= 8000k (sin θcos θ+ cos θ) ,θ∈[θ ,π) .0 2 设 f (θ) = sin θcos θ+ cos θ,θ∈[θ ,π) ,0 2则 f '(θ) = cos 2 θ- sin 2 θ- sin θ= -(2 sin 2 θ+ sin θ-1) = -(2 sin θ-1)(sin θ+1) . π令 f '(θ) = 0 ,得θ= 6 ,当θ∈ (θ ,π) 时, f ′(θ)>0,所以 f (θ)为增函数;0 6当θ∈ (π,π) 时, f ′(θ)<0 ,所以 f (θ) 为减函数, 6 2π因此,当θ= 6时, f (θ) 取到最大值.π答:当θ= 6时,能使甲、乙两种蔬菜的年总产值最大.15.【解析】(1)由log 2 ⎭ + 5 >1 ,解得 x ∈⎛-∞, - 1 ⎫ (0, +∞).4 ⎪ ⎝ ⎭ (2) 1+ a = (a - 4)x + 2a - 5 ,(a - 4) x 2 +(a -5)x -1= 0 ,x当a = 4 时, x = -1 ,经检验,满足题意.当a = 3时, x 1 = x 2 = -1,经检验,满足题意.当a ≠ 3 且a ≠ 4 时, x 1 =1a - 4 ,x 2 = -1 , x 1 ≠ x 2 . x 1 是原方程的解当且仅当 1+ a > 0 ,即a > 2 ;x 1 x 2 是原方程的解当且仅当 1+ a > 0 ,即a >1 .x 2于是满足题意的a ∈(1, 2] .⎛ 1 + 5 ⎫> 0 ,得 1⎝x ⎪ x1 ⎩ ⎭综上,a 的取值范围为(1, 2] {3, 4}.(3)当0 < x < x 时, + a > 1 + a ,log ⎛ 1 + a ⎫> log ⎛ 1 + a ⎫ , 1 2xx2 x ⎪ 2 x⎪ 1 2所以 f (x )在 (0, +∞)上单调递减.⎝ 1 ⎭ ⎝ 2 ⎭函数 f (x )在区间 [t ,t +1]上的最大值与最小值分别为 f (t ) , f (t +1) .f (t ) - f (t +1) = log⎛ 1 + a ⎫ - log ⎛ 1 + a ⎫≤ 1 即at 2 + (a +1)t -1≥ 0 , 2 t ⎪ 2 t +1 ⎪ ⎝ ⎭ ⎝ ⎭对任意t ∈⎡1 ,1⎤成立. ⎢⎣2 ⎥⎦因为 a > 0 ,所以函数 y = at 2 + (a +1)t -1在区间⎡ 1 ,1⎤上单调递增, ⎢⎣ 2 ⎥⎦t = 1 时, y 有最小值3 a - 1 ,由 3 a - 1 ≥ 0,得a ≥ 2 .2 4 2 4 2 3故a 的取值范围为⎡ 2 , +∞⎫.⎢⎣ 3 ⎪16.【解析】(1)由题意知,点M , N 的坐标分别为(5, 40) ,(20, 2.5) .⎧ a= 40将其分别代入y = a,得⎪ 25+ b ⎧a = 1000 ,解得. x 2+ b⎨ a ⎨b = 0⎪ 400+ b = 2.5(2)①由(1)知, y = 1000 ( 5 ≤ x ≤ 20 ),则点P 的坐标为 ⎛t , 1000⎫ ,x 2t2 ⎪ ⎝ ⎭ 设在点P 处的切线l 交 x , y 轴分别于 A , B 点, y ' = - 2000,x3 则l 的方程为 y - 1000 = - 2000 ( x - t ),由此得A ⎛ 3t , 0 ⎫, B ⎛ 0, 3000⎫. t 2 t 32 ⎪ t 2 ⎪⎛ 3t ⎫2⎛ 3000 ⎫23 24 ⨯106 ⎝ ⎭ ⎝ ⎭ t ∈ 5, 20故 f (t ) = 2 ⎪ + t 2 ⎪ = 2 t + t 4 , [ ].⎝ ⎭ ⎝ ⎭②设 g (t ) = t 2 + 4 ⨯10 6 ,则g '(t ) = 2t - 16⨯106.令g '(t )= 0 ,解得t 10 2 .t 4 t 5=⎩当t ∈(5,10 2)时,g '(t )< 0 , g (t ) 是减函数;当t ∈(10 2, 20) 时, g '(t )> 0 ,g (t ) 是增函数. 从而,当t = 10 2 时,函数g (t )有极小值,也是最小值,所以g (t )min = 300 ,此时 f (t )min = 15 3 .答:当t = 10 2 时,公路l 的长度最短,最短长度为15 3 千米.17.【解析】(Ⅰ)因为蓄水池侧面积的总成本为100⋅2πrh = 200πrh 元,底面的总成本为160πr 2 元,所以蓄水池的总成本为( 200πrh +160πr 2 )元.又题意据200πrh +160πr 2=12000π,所以h =1(300 - 4r 2 ) ,5r从而V (r ) =πr 2h = π(300r - 4r 3) .因r > 0 ,又由h > 0 可得r < 5 3 ,5故函数V (r ) 的定义域为(0, 5 3) .(Ⅱ)因V (r ) = π(300r - 4r 3 ) ,故V '(r ) = π(300 -12r 2) .令V '(r ) = 0 ,5 5解得r 1 = 5, r 2 = -5 (因 r 2 = -5不在定义域内,舍去). 当r ∈ (0,5) 时,V '(r ) > 0 ,故V (r ) 在 (0, 5) 上为增函数;当r ∈(5,5 3) 时,V '(r ) < 0 ,故V (r ) 在(5, 5 3) 上为减函数. 由此可知,V (r ) 在r = 5 处取得最大值,此时h = 8 . 即当r = 5 , h = 8时,该蓄水池的体积最大.18.【解析】(1)当b = 1,c = -1, n …2 时, f (x ) = x n+ x - 1.∵ f (1) f (1) = ( 1 - 1 )⨯1< 0 ,∴ f (x ) 在( 1,1) 内存在零点.2 2n 2 2又当 x ∈( 1 ,1) 时, f '(x ) = nx n -1+ 1> 0 ,∴ f (x ) 在( 1 ,1) 上是单调递增的,2 2∴ f (x ) 在区间( 1,1) 内存在唯一的零点;2⎧-1剟f (-1) 1, ⎧ 0 剟b - c 2, (2)解法一 由题意知 ⎨ -1剟f (1) 1, 即 ⎨-2 剟b + c 0, 由图像知,b + 3c 在点⎩ ⎩(0, -2) 取得最小值-6 ,在点(0, 0) 取得最大值0 .⎨-1剟f (1) 1,cO b - 2解法二 由题意知-1剟f (1) =1+b +c 1 ,即-2 剟b +c0 .…①-1剟f (-1) =1-b +c1,即-2 ? --b +c ?0 .…②①⨯2 +②得-6 ? 2(-b +c) + (-b +c) =b + 3c ? 0当b = 0, c =-2 时,b + 3c =-6 ;当b =c = 0 时,b + 3c = 0所以b + 3c 的最小值-6 ,最大值0 .⎧f (-1) =1 -b +c,解法三由题意知⎨⎩ f (1) =1 +b +c,,解得b = f (1) -f ( -1) , c = f (1) +f ( -1) -22 2b + 3c = 2 f (1) +f (-1) - 3 .又∵⎧-1剟f (-1) 1,, ∴-6 ?b +3c ? 0⎩当b = 0, c =-2 时,b +3c =-6 ;当b =c = 0 时,b +3c = 0 所以b + 3c 的最小值-6 ,最大值0 .(3)当n = 2 时, f (x) =x2 +bx +c .对任意x1, x2∈[-1,1] 都有有 f (x1) -f (x2) …4 等价于f (x) 在[-1,1]上的最大值与最小值之差M … 4 .据此分类讨论如下:(ⅰ)当b>1 ,即b > 2时,2M =f (1) -f (-1) = 2 b > 4 ,与题设矛盾.(ⅱ)当-1…-b<0 ,即0 <b …22 时,M =f (1)-f (-b) = (b+ 1)2 …2 24 恒成立.(ⅲ) 当0 …-b<1 ,即-2 剟b20 时, M =f (-1)-f (-b) =(b-1)2 …2 24 恒成立.综上可知, -2 剟b 2 . 19.【解析】设包装盒的高为h (cm ),底面边长为a (cm ),由已知得 2 (1) S = 4ah = 8x (30 - x ) = -8( x -15)2 +1800, 所以当x = 15 时, S 取得最大值. (2)V = a 2h = 2 2 - (x 2 + 30x 2 ),V ' = 6 2x (20- x ). a = 2x ,h = 60 - 2x = 2(30 - x ),0 < x < 30. 由V ' = 0得x = 0 (舍)或x =20. 当 x ∈ (0,20) 时,V ' > 0;当x ∈ (20, 30)时V ' < 0 . 所以当 x =20 时,V 取得极大值,也是最小值. 此时 h = 1 即1 装盒的高与底面边长的比值 a 2 2 2。

专题二 函数概念与基本初等函数Ⅰ第六讲函数的综合及其应用一、选择题1.(2017天津)已知函数23,1,()2, 1.x x x f x x x x ⎧-+⎪=⎨+>⎪⎩≤设a ∈R ,若关于x 的不等式()||2x f x a +≥在R 上恒成立,则a 的取值范围是 A .47[,2]16-B .4739[,]1616-C .[23,2]-D .39[23,]16- 2.(2015北京)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是A .消耗1升汽油,乙车最多可行驶5千米B .以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多C .甲车以80千米/小时的速度行驶1小时,消耗10升汽油D .某城市机动车最高限速80千米/小时.相同条件下,在该市用丙车比用乙车更省油 3.(2014北京)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p 与加工时间t (单位:分钟)满足函数关系2p at bt c =++(a 、b 、c 是常数),下图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( )A .3.50分钟B .3.75分钟C .4.00分钟D .4.25分钟4.(2014湖南)某市生产总值连续两年持续增加,第一年的增长率为p ,第二年的增长率为q ,则该市这两年生产总值的年平均增长率为 A .2p q + B .(1)(1)12p q ++- CD1 二、填空题5.(2017山东)若函数e ()xf x (e=2.71828L ,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是 . ①()2xf x -=②2()f x x=③()3xf x -=④()cos f x x =6.(2017江苏)设()f x 是定义在R 且周期为1的函数,在区间[0,1)上,2,(),x x Df x x x D⎧∈=⎨∉⎩其中集合1{|,}n D x x n n-==∈*N ,则方程()lg 0f x x -=的解的个数是 .7.(2017新课标Ⅰ)如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC的中心为O .D 、E 、F 为圆O 上的点,DBC ∆,ECA ∆,FAB ∆分别是以BC ,CA ,AB 为底边的等腰三角形。
专题02函数的概念与基本初等函数1.【2019年天津理科06】已知a=log52,b=log0.50.2,c=0.50.2,则a,b,c的大小关系为()A.a<c<b B.a<b<c C.b<c<a D.c<a<b【解答】解:由题意,可知:a=log52<1,b=log0.50.2log25>log24=2.c=0.50.2<1,∴b最大,a、c都小于1.∵a=log52,c=0.50.2.而log25>log24=2,∴.∴a<c,∴a<c<b.故选:A.2.【2019年天津理科08】已知a∈R.设函数f(x)若关于x的不等式f(x)≥0在R上恒成立,则a的取值范围为()A.[0,1] B.[0,2] C.[0,e] D.[1,e]【解答】解:当x=1时,f(1)=1﹣2a+2a=1>0恒成立;当x<1时,f(x)=x2﹣2ax+2a≥0⇔2a恒成立,令g(x)(1﹣x2)≤﹣(22)=0,∴2a≥g(x)max=0,∴a>0.当x>1时,f(x)=x﹣alnx≥0⇔a恒成立,令h(x),则h′(x),当x>e时,h′(x)>0,h(x)递增,当1<x<e时,h′′(x)<0,h(x)递减,∴x=e时,h(x)取得最小值h(e)=e,∴a≤h(x)e,综上a的取值范围是[0,e].故选:C.3.【2019年新课标3理科11】设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则()A.f(log3)>f(2)>f(2)B.f(log3)>f(2)>f(2)C.f(2)>f(2)>f(log3)D.f(2)>f(2)>f(log3)【解答】解:∵f(x)是定义域为R的偶函数∴,∵log34>log33=1,,∴0f(x)在(0,+∞)上单调递减,∴,故选:C.4.【2019年全国新课标2理科12】设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x(x﹣1).若对任意x∈(﹣∞,m],都有f(x),则m的取值范围是()A.(﹣∞,] B.(﹣∞,] C.(﹣∞,] D.(﹣∞,]【解答】解:因为f(x+1)=2f(x),∴f(x)=2f(x﹣1),∵x∈(0,1]时,f(x)=x(x﹣1)∈[,0],∴x∈(1,2]时,x﹣1∈(0,1],f(x)=2f(x﹣1)=2(x﹣1)(x﹣2)∈[,0];∴x∈(2,3]时,x﹣1∈(1,2],f(x)=2f(x﹣1)=4(x﹣2)(x﹣3)∈[﹣1,0],当x∈(2,3]时,由4(x﹣2)(x﹣3)解得m或m,若对任意x∈(﹣∞,m],都有f(x),则m.故选:B.5.【2019年新课标1理科03】已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a【解答】解:a=log20.2<log21=0,b=20.2>20=1,∵0<0.20.3<0.20=1,∴c=0.20.3∈(0,1),∴a<c<b,故选:B.6.【2019年浙江06】在同一直角坐标系中,函数y,y=1og a(x)(a>0且a≠1)的图象可能是()A.B.C.D.【解答】解:由函数y,y=1og a(x),当a>1时,可得y是递减函数,图象恒过(0,1)点,函数y=1og a(x),是递增函数,图象恒过(,0);当1>a>0时,可得y是递增函数,图象恒过(0,1)点,函数y=1og a(x),是递减函数,图象恒过(,0);∴满足要求的图象为:D故选:D.7.【2019年浙江09】设a,b∈R,函数f(x)若函数y=f(x)﹣ax﹣b 恰有3个零点,则()A.a<﹣1,b<0 B.a<﹣1,b>0 C.a>﹣1,b<0 D.a>﹣1,b>0【解答】解:当x<0时,y=f(x)﹣ax﹣b=x﹣ax﹣b=(1﹣a)x﹣b=0,得x;y=f(x)﹣ax﹣b最多一个零点;当x≥0时,y=f(x)﹣ax﹣b x3(a+1)x2+ax﹣ax﹣b x3(a+1)x2﹣b,y′=x2﹣(a+1)x,当a+1≤0,即a≤﹣1时,y′≥0,y=f(x)﹣ax﹣b在[0,+∞)上递增,y=f(x)﹣ax﹣b最多一个零点.不合题意;当a+1>0,即a<﹣1时,令y′>0得x∈[a+1,+∞),函数递增,令y′<0得x∈[0,a+1),函数递减;函数最多有2个零点;根据题意函数y=f(x)﹣ax﹣b恰有3个零点⇔函数y=f(x)﹣ax﹣b在(﹣∞,0)上有一个零点,在[0,+∞)上有2个零点,如右图:∴0且,解得b<0,1﹣a>0,b(a+1)3.故选:C.8.【2018年新课标1理科09】已知函数f(x),g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是()A.[﹣1,0)B.[0,+∞)C.[﹣1,+∞)D.[1,+∞)【解答】解:由g(x)=0得f(x)=﹣x﹣a,作出函数f(x)和y=﹣x﹣a的图象如图:当直线y=﹣x﹣a的截距﹣a≤1,即a≥﹣1时,两个函数的图象都有2个交点,即函数g(x)存在2个零点,故实数a的取值范围是[﹣1,+∞),故选:C.9.【2018年新课标2理科11】已知f(x)是定义域为(﹣∞,+∞)的奇函数,满足f(1﹣x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.﹣50 B.0 C.2 D.50【解答】解:∵f(x)是奇函数,且f(1﹣x)=f(1+x),∴f(1﹣x)=f(1+x)=﹣f(x﹣1),f(0)=0,则f(x+2)=﹣f(x),则f(x+4)=﹣f(x+2)=f(x),即函数f(x)是周期为4的周期函数,∵f(1)=2,∴f(2)=f(0)=0,f(3)=f(1﹣2)=f(﹣1)=﹣f(1)=﹣2,f(4)=f(0)=0,则f(1)+f(2)+f(3)+f(4)=2+0﹣2+0=0,则f(1)+f(2)+f(3)+…+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(49)+f(50)=f(1)+f(2)=2+0=2,故选:C.10.【2018年新课标3理科12】设a=log0.20.3,b=log20.3,则()A.a+b<ab<0 B.ab<a+b<0 C.a+b<0<ab D.ab<0<a+b【解答】解:∵a=log0.20.3,b=log20.3,∴,,∵,,∴ab<a+b<0.故选:B.11.【2018年上海16】设D是含数1的有限实数集,f(x)是定义在D上的函数,若f(x)的图象绕原点逆时针旋转后与原图象重合,则在以下各项中,f(1)的可能取值只能是()A.B.C.D.0【解答】解:由题意得到:问题相当于圆上由12个点为一组,每次绕原点逆时针旋转个单位后与下一个点会重合.我们可以通过代入和赋值的方法当f(1),,0时,此时得到的圆心角为,,0,然而此时x=0或者x=1时,都有2个y与之对应,而我们知道函数的定义就是要求一个x只能对应一个y,因此只有当x,此时旋转,此时满足一个x只会对应一个y,因此答案就选:B.故选:B.12.【2018年北京理科04】“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献,十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f,则第八个单音的频率为()A.f B.f C.f D.f【解答】解:从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f,则第八个单音的频率为:.故选:D.13.【2018年天津理科05】已知a=log2e,b=ln2,c,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b【解答】解:a=log2e>1,0<b=ln2<1,c log23>log2e=a,则a,b,c的大小关系c>a>b,故选:D.14.【2017年新课标1理科05】函数f(x)在(﹣∞,+∞)单调递减,且为奇函数.若f(1)=﹣1,则满足﹣1≤f(x﹣2)≤1的x的取值范围是()A.[﹣2,2] B.[﹣1,1] C.[0,4] D.[1,3]【解答】解:∵函数f(x)为奇函数.若f(1)=﹣1,则f(﹣1)=1,又∵函数f(x)在(﹣∞,+∞)单调递减,﹣1≤f(x﹣2)≤1,∴f(1)≤f(x﹣2)≤f(﹣1),∴﹣1≤x﹣2≤1,解得:x∈[1,3],故选:D.15.【2017年新课标1理科11】设x、y、z为正数,且2x=3y=5z,则()A.2x<3y<5z B.5z<2x<3y C.3y<5z<2x D.3y<2x<5z【解答】解:x、y、z为正数,令2x=3y=5z=k>1.lgk>0.则x,y,z.∴3y,2x,5z.∵,.∴lg0.∴3y<2x<5z.另解:x、y、z为正数,令2x=3y=5z=k>1.lgk>0.则x,y,z.∴1,可得2x>3y,1.可得5z>2x.综上可得:5z>2x>3y.解法三:对k取特殊值,也可以比较出大小关系.故选:D.16.【2017年浙江05】若函数f(x)=x2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M﹣m()A.与a有关,且与b有关B.与a有关,但与b无关C.与a无关,且与b无关D.与a无关,但与b有关【解答】解:函数f(x)=x2+ax+b的图象是开口朝上且以直线x为对称轴的抛物线,①当1或0,即a<﹣2,或a>0时,函数f(x)在区间[0,1]上单调,此时M﹣m=|f(1)﹣f(0)|=|a+1|,故M﹣m的值与a有关,与b无关②当1,即﹣2≤a≤﹣1时,函数f(x)在区间[0,]上递减,在[,1]上递增,且f(0)>f(1),此时M﹣m=f(0)﹣f(),故M﹣m的值与a有关,与b无关③当0,即﹣1<a≤0时,函数f(x)在区间[0,]上递减,在[,1]上递增,且f(0)<f(1),此时M﹣m=f(1)﹣f()=1+a,故M﹣m的值与a有关,与b无关综上可得:M﹣m的值与a有关,与b无关故选:B.17.【2017年北京理科05】已知函数f(x)=3x﹣()x,则f(x)()A.是奇函数,且在R上是增函数B.是偶函数,且在R上是增函数C.是奇函数,且在R上是减函数D.是偶函数,且在R上是减函数【解答】解:f(x)=3x﹣()x=3x﹣3﹣x,∴f(﹣x)=3﹣x﹣3x=﹣f(x),即函数f(x)为奇函数,又由函数y=3x为增函数,y=()x为减函数,故函数f(x)=3x﹣()x为增函数,故选:A.18.【2017年北京理科08】根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080,则下列各数中与最接近的是()(参考数据:lg3≈0.48)A.1033B.1053C.1073D.1093【解答】解:由题意:M≈3361,N≈1080,根据对数性质有:3=10lg3≈100.48,∴M≈3361≈(100.48)361≈10173,∴1093,故选:D.19.【2017年天津理科06】已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(﹣log25.1),b =g(20.8),c=g(3),则a,b,c的大小关系为()A.a<b<c B.c<b<a C.b<a<c D.b<c<a【解答】解:奇函数f(x)在R上是增函数,当x>0,f(x)>f(0)=0,且f′(x)>0,∴g(x)=xf(x),则g′(x)=f(x)+xf′(x)>0,∴g(x)在(0,+∞)单调递增,且g(x)=xf(x)偶函数,∴a=g(﹣log25.1)=g(log25.1),则2<log25.1<3,1<20.8<2,由g(x)在(0,+∞)单调递增,则g(20.8)<g(log25.1)<g(3),∴b<a<c,故选:C.20.【2017年天津理科08】已知函数f(x),设a∈R,若关于x的不等式f(x)≥|a|在R上恒成立,则a的取值范围是()A.[,2] B.[,] C.[﹣2,2] D.[﹣2,]【解答】解:当x≤1时,关于x的不等式f(x)≥|a|在R上恒成立,即为﹣x2+x﹣3a≤x2﹣x+3,即有﹣x2x﹣3≤a≤x2x+3,由y=﹣x2x﹣3的对称轴为x1,可得x处取得最大值;由y=x2x+3的对称轴为x1,可得x处取得最小值,则a①当x>1时,关于x的不等式f(x)≥|a|在R上恒成立,即为﹣(x)a≤x,即有﹣(x)≤a,由y=﹣(x)≤﹣22(当且仅当x1)取得最大值﹣2;由y x22(当且仅当x=2>1)取得最小值2.则﹣2a≤2②由①②可得,a≤2.另解:作出f(x)的图象和折线y=|a|当x≤1时,y=x2﹣x+3的导数为y′=2x﹣1,由2x﹣1,可得x,切点为(,)代入y a,解得a;当x>1时,y=x的导数为y′=1,由1,可得x=2(﹣2舍去),切点为(2,3),代入y a,解得a=2.由图象平移可得,a≤2.故选:A.21.【2019年全国新课标2理科14】已知f(x)是奇函数,且当x<0时,f(x)=﹣e ax.若f(ln2)=8,则a=.【解答】解:∵f(x)是奇函数,∴f(﹣ln2)=﹣8,又∵当x<0时,f(x)=﹣e ax,∴f(﹣ln2)=﹣e﹣aln2=﹣8,∴﹣aln2=ln8,∴a=﹣3.故答案为:﹣322.【2019年江苏04】函数y的定义域是.【解答】解:由7+6x﹣x2≥0,得x2﹣6x﹣7≤0,解得:﹣1≤x≤7.∴函数y的定义域是[﹣1,7].故答案为:[﹣1,7].23.【2019年江苏14】设f(x),g(x)是定义在R上的两个周期函数,f(x)的周期为4,g(x)的周期为2,且f(x)是奇函数.当x∈(0,2]时,f(x),g(x)其中k>0.若在区间(0,9]上,关于x的方程f(x)=g(x)有8个不同的实数根,则k的取值范围是.【解答】解:作出函数f(x)与g(x)的图象如图,由图可知,函数f(x)与g(x)(1<x≤2,3<x≤4,5<x≤6,7<x≤8)仅有2个实数根;要使关于x的方程f(x)=g(x)有8个不同的实数根,则f(x),x∈(0,2]与g(x)=k(x+2),x∈(0,1]的图象有2个不同交点,由(1,0)到直线kx﹣y+2k=0的距离为1,得,解得k(k>0),∵两点(﹣2,0),(1,1)连线的斜率k,∴k.即k的取值范围为[,).故答案为:[,).24.【2018年江苏05】函数f(x)的定义域为.【解答】解:由题意得:log2x≥1,解得:x≥2,∴函数f(x)的定义域是[2,+∞).故答案为:[2,+∞).25.【2018年江苏09】函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f(x),则f(f(15))的值为.【解答】解:由f(x+4)=f(x)得函数是周期为4的周期函数,则f(15)=f(16﹣1)=f(﹣1)=|﹣1|,f()=cos()=cos,即f(f(15)),故答案为:26.【2018年浙江11】我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一.凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁,鸡母,鸡雏个数分别为x,y,z,则,当z=81时,x=,y=.【解答】解:,当z=81时,化为:,解得x=8,y=11.故答案为:8;11.27.【2018年浙江15】已知λ∈R,函数f(x),当λ=2时,不等式f(x)<0的解集是.若函数f(x)恰有2个零点,则λ的取值范围是.【解答】解:当λ=2时函数f(x),显然x≥2时,不等式x﹣4<0的解集:{x|2≤x<4};x<2时,不等式f(x)<0化为:x2﹣4x+3<0,解得1<x<2,综上,不等式的解集为:{x|1<x<4}.函数f(x)恰有2个零点,函数f(x)的草图如图:函数f(x)恰有2个零点,则1<λ≤3或λ>4.故答案为:{x|1<x<4};(1,3]∪(4,+∞).28.【2018年上海04】设常数a∈R,函数f(x)=1og2(x+a).若f(x)的反函数的图象经过点(3,1),则a=.【解答】解:∵常数a∈R,函数f(x)=1og2(x+a).f(x)的反函数的图象经过点(3,1),∴函数f(x)=1og2(x+a)的图象经过点(1,3),∴log2(1+a)=3,解得a=7.故答案为:7.29.【2018年上海07】已知α∈{﹣2,﹣1,,1,2,3},若幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,则α=.【解答】解:∵α∈{﹣2,﹣1,,1,2,3},幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,∴a是奇数,且a<0,∴a=﹣1.故答案为:﹣1.30.【2018年上海11】已知常数a>0,函数f(x)的图象经过点P(p,),Q(q,).若2p+q=36pq,则a=.【解答】解:函数f(x)的图象经过点P(p,),Q(q,).则:,整理得:1,解得:2p+q=a2pq,由于:2p+q=36pq,所以:a2=36,由于a>0,故:a=6.故答案为:631.【2018年北京理科13】能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是.【解答】解:例如f(x)=sin x,尽管f(x)>f(0)对任意的x∈(0,2]都成立,当x∈[0,)上为增函数,在(,2]为减函数,故答案为:f(x)=sin x.32.【2018年天津理科14】已知a>0,函数f(x).若关于x的方程f(x)=ax 恰有2个互异的实数解,则a的取值范围是.【解答】解:当x≤0时,由f(x)=ax得x2+2ax+a=ax,得x2+ax+a=0,得a(x+1)=﹣x2,得a,设g(x),则g′(x),由g′(x)>0得﹣2<x<﹣1或﹣1<x<0,此时递增,由g′(x)<0得x<﹣2,此时递减,即当x=﹣2时,g(x)取得极小值为g(﹣2)=4,当x>0时,由f(x)=ax得﹣x2+2ax﹣2a=ax,得x2﹣ax+2a=0,得a(x﹣2)=x2,当x=2时,方程不成立,当x≠2时,a设h(x),则h′(x),由h′(x)>0得x>4,此时递增,由h′(x)<0得0<x<2或2<x<4,此时递减,即当x=4时,h(x)取得极小值为h(4)=8,要使f(x)=ax恰有2个互异的实数解,则由图象知4<a<8,故答案为:(4,8)33.【2017年江苏14】设f(x)是定义在R上且周期为1的函数,在区间[0,1)上,f(x),其中集合D={x|x,n∈N*},则方程f(x)﹣lgx=0的解的个数是.【解答】解:∵在区间[0,1)上,f(x),第一段函数上的点的横纵坐标均为有理数,又f(x)是定义在R上且周期为1的函数,∴在区间[1,2)上,f(x),此时f(x)的图象与y=lgx有且只有一个交点;同理:区间[2,3)上,f(x)的图象与y=lgx有且只有一个交点;区间[3,4)上,f(x)的图象与y=lgx有且只有一个交点;区间[4,5)上,f(x)的图象与y=lgx有且只有一个交点;区间[5,6)上,f(x)的图象与y=lgx有且只有一个交点;区间[6,7)上,f(x)的图象与y=lgx有且只有一个交点;区间[7,8)上,f(x)的图象与y=lgx有且只有一个交点;区间[8,9)上,f(x)的图象与y=lgx有且只有一个交点;在区间[9,+∞)上,f(x)的图象与y=lgx无交点;故f(x)的图象与y=lgx有8个交点,且除了(1,0),其他交点横坐标均为无理数;即方程f(x)﹣lgx=0的解的个数是8,故答案为:834.【2017年新课标3理科15】设函数f(x),则满足f(x)+f(x)>1的x的取值范围是.【解答】解:若x≤0,则x,则f(x)+f(x)>1等价为x+1+x1>1,即2x,则x,此时x≤0,当x>0时,f(x)=2x>1,x,当x0即x时,满足f(x)+f(x)>1恒成立,当0≥x,即x>0时,f(x)=x1=x,此时f(x)+f(x)>1恒成立,综上x,故答案为:(,+∞).35.【2017年浙江17】已知a∈R,函数f(x)=|x a|+a在区间[1,4]上的最大值是5,则a的取值范围是.【解答】解:由题可知|x a|+a≤5,即|x a|≤5﹣a,所以a≤5,又因为|x a|≤5﹣a,所以a﹣5≤x a≤5﹣a,所以2a﹣5≤x5,又因为1≤x≤4,4≤x5,所以2a﹣5≤4,解得a,故答案为:(﹣∞,].36.【2017年上海08】定义在(0,+∞)上的函数y=f(x)的反函数为y=f﹣1(x),若g(x)为奇函数,则f﹣1(x)=2的解为.【解答】解:若g(x)为奇函数,可得当x>0时,﹣x<0,即有g(﹣x)=3﹣x﹣1,由g(x)为奇函数,可得g(﹣x)=﹣g(x),则g(x)=f(x)=1﹣3﹣x,x>0,由定义在(0,+∞)上的函数y=f(x)的反函数为y=f﹣1(x),且f﹣1(x)=2,可由f(2)=1﹣3﹣2,可得f﹣1(x)=2的解为x.故答案为:.37.【2017年上海09】已知四个函数:①y=﹣x,②y,③y=x3,④y,从中任选2个,则事件“所选2个函数的图象有且仅有一个公共点”的概率为.【解答】解:给出四个函数:①y=﹣x,②y,③y=x3,④y,从四个函数中任选2个,基本事件总数n,③④有两个公共点(0,0),(1,1).事件A:“所选2个函数的图象有且只有一个公共点”包含的基本事件有:①③,①④共2个,∴事件A:“所选2个函数的图象有且只有一个公共点”的概率为P(A).故答案为:.38.【2019年江苏18】如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB (AB是圆O的直径).规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA,规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).(1)若道路PB与桥AB垂直,求道路PB的长;(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;(3)在规划要求下,若道路PB和QA的长度均为d(单位:百米),求当d最小时,P、Q两点间的距离.【解答】解:设BD与圆O交于M,连接AM,AB为圆O的直径,可得AM⊥BM,即有DM=AC=6,BM=6,AM=8,以C为坐标原点,l为x轴,建立直角坐标系,则A(0,﹣6),B(﹣8,﹣12),D(﹣8,0)(1)设点P(x1,0),PB⊥AB,则k BP•k AB=﹣1,即•1,解得x1=﹣17,所以P(﹣17,0),PB15;(2)当QA⊥AB时,QA上的所有点到原点O的距离不小于圆的半径,设此时Q(x2,0),则k QA•k AB=﹣1,即•1,解得x2,Q(,0),由﹣17<﹣8,在此范围内,不能满足PB,QA上所有点到O的距离不小于圆的半径,所以P,Q中不能有点选在D点;(3)设P(a,0),Q(b,0),则a≤﹣17,b,PB2=(a+8)2+144≥225,QA2=b2+36≥225,则b≥3,当d最小时,PQ=17+3.39.【2018年上海19】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族S中的成员仅以自驾或公交方式通勤.分析显示:当S中x%(0<x<100)的成员自驾时,自驾群体的人均通勤时间为f(x)(单位:分钟),而公交群体的人均通勤时间不受x影响,恒为40分钟,试根据上述分析结果回答下列问题:(1)当x在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族S的人均通勤时间g(x)的表达式;讨论g(x)的单调性,并说明其实际意义.【解答】解;(1)由题意知,当30<x<100时,f (x )=2x90>40,即x 2﹣65x +900>0,解得x <20或x >45,∴x ∈(45,100)时,公交群体的人均通勤时间少于自驾群体的人均通勤时间; (2)当0<x ≤30时,g (x )=30•x %+40(1﹣x %)=40;当30<x <100时,g (x )=(2x 90)•x %+40(1﹣x %)x +58;∴g (x );当0<x <32.5时,g (x )单调递减; 当32.5<x <100时,g (x )单调递增;说明该地上班族S 中有小于32.5%的人自驾时,人均通勤时间是递减的; 有大于32.5%的人自驾时,人均通勤时间是递增的; 当自驾人数为32.5%时,人均通勤时间最少.1.【山西省晋城市2019届高三第三次模拟考试】若函数(()sin ln f x x ax =⋅的图象关于y 轴对称,则实数a 的值为( ) A .2 B .4C .2±D .4±【答案】C 【解析】依题意,函数()f x 为偶函数.由于()sin m x x =为奇函数,故(()ln g x ax =也为奇函数.而(()ln g x ax -=-+,故((()()ln ln 0g x g x ax ax -+=-+++=,即()222ln 140x a x +-=,解得2a =±.故选:C.2.【广东省东莞市2019届高三第二学期高考冲刺试题(最后一卷)】己知()f x 是定义在R 上的偶函数,在区间(]0-∞,为增函数,且()30f =,则不等式(12)0f x ->的解集为( ) A .()10-,B .()12-,C .()02,D .()2,+∞ 【答案】B 【解析】根据题意,因为f (x )是定义在R 上的偶函数,且在区间(一∞,0]为增函数, 所以函数f (x )在[0,+∞)上为减函数,由f (3)=0,则不等式f (1﹣2x )>0⇒f (1﹣2x )>f (3)⇒|1﹣2x|<3, 解可得:﹣1<x <2,即不等式的解集为(﹣1,2). 故选:B .3.【天津市河北区2019届高三一模】已知()f x 是定义在R 上的偶函数,且()f x 在[)0,+∞内单调递减,则( )A .()()()320log 2log 3f f f <<-B .()()()32log 20log 3f f f <<-C .()()()23log 3log 20f f f -<<D .()()()32log 2log 30f f f <-<【答案】C 【解析】∵f (x )为偶函数∴()()22f log 3?f log 3-= ∵320log 21,log 31,< f (x )在[0,+∞)内单调递减,∴()()()23f log 3f log 2f 0<<,即()()()23f log 3f log 2f 0-<<故选:C4.【天津市红桥区2019届高三二模】已知 1.22a =,52log 2=b ,1ln 3c =,则( ) A .a b c >> B .a c b >>C .b a c >>D .b c a >>【答案】A【解析】1.21222a =>=5552log 2log 4log 51b ==<=且55log 4log 10b =>=1ln ln3ln 13c e ==-<-=-即1012c b a <-<<<<<a b c ∴>>本题正确选项:A5.【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】已知函数()221log 2xf x x+=-,若()f a b =,则()4f a -=( )A .bB .2b -C .b -D .4b -【答案】B 【解析】因为()()()()22222213log log log 42222x xf x f x x x -++-=+==--- 故函数()f x 关于点(2,1)对称,则()4f a -=2b - 故选:B6.【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】已知函数()21x f x x =-,则( )A .()f x 在()0,1单调递增B .()f x 的最小值为4C .()y f x =的图象关于直线1x =对称D .()y f x =的图象关于点()1,2对称【答案】D 【解析】由题意知:()()()()()()222222122111x x x x x x xf x x x x ----'===---当()0,1x ∈时,()0f x '<,则()f x 在()0,1上单调递减,A 错误; 当10x -<时,()0f x <,可知()f x 最小值为4不正确,B 错误;()()()22221x f x f x x --=≠--,则()f x 不关于1x =对称,C 错误; ()()()()2211114x x f x f x xx+-++-=+=-,则()f x 关于()1,2对称,D 正确.本题正确选项:D7.【山东省栖霞市2019届高三高考模拟卷(新课标I)】已知定义在R 上的奇函数()f x 满足(2)()f x f x +=-,当01x ≤≤时,2()f x x =,则(1)(2)(3)(2019)f f f f ++++=L ( )A .2019B .0C .1D .-1【答案】B 【解析】由()()()42f x f x f x +=-+=得:()f x 的周期为4 又()f x 为奇函数()11f ∴=,()()200f f =-=,()()()3111f f f =-=-=-,()()400f f ==即:()()()()12340f f f f +++=()()()()()()()()()1232019505123440f f f f f f f f f ∴+++⋅⋅⋅=⨯+++-=⎡⎤⎣⎦本题正确选项:B8.【天津市红桥区2019届高三一模】若方程2121x kx x -=--有两个不同的实数根,则实数k 的取值范围是( ) A .(),1-∞- B .()1,0-C .()0,4D .()()0,11,4【答案】D 【解析】 解:y 211111111x x x x x x x -+-⎧==⎨----⎩,>或<,<<, 画出函数y =kx ﹣2,y 211x x -=-的图象,由图象可以看出,y =kx ﹣2图象恒过A (0,﹣2),B (1,2),AB 的斜率为4,①当0<k <1时,函数y =kx ﹣2,y 211x x -=-的图象有两个交点,即方程211x x -=-kx ﹣2有两个不同的实数根;②当k =1时,函数y =kx ﹣2,y 211x x -=-的图象有1个交点,即方程211x x -=-kx ﹣2有1个不同的实数根;③当1<k <4时,函数y =kx ﹣2,y 211x x -=-的图象有两个交点,即方程211x x -=-kx ﹣2有两个不同的实数根;④当k 0≤时,函数y =kx ﹣2,y 211x x -=-的图象有1个交点.因此实数k 的取值范围是0<k <1或1<k <4. 故选:D .9.【天津市部分区2019届高三联考一模】设,m n R ∈,则“m n <”是“112m n-⎛⎫> ⎪⎝⎭”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】C 【解析】()12xf x ⎛⎫= ⎪⎝⎭在R 上递减,∴若011,0,122m nm n m n -⎛⎫⎛⎫<-<>= ⎪ ⎪⎝⎭⎝⎭充分性成立, 若112m n-⎛⎫> ⎪⎝⎭,则01122m n-⎛⎫⎛⎫> ⎪⎪⎝⎭⎝⎭, 0,m n m n -<<必要性成立,即“m n <”是“112m n-⎛⎫> ⎪⎝⎭”的充要条件,故选C.10.【广东省2019届高考适应性考试】某罐头加工厂库存芒果()m kg ,今年又购进()n kg 新芒果后,欲将芒果总量的三分之一用于加工为芒果罐头。
专题02 函数概念与基本初等函数
(新定义,高数观点,选填压轴题)
目录
一、函数及其表示 (1)
二、函数的基本性质 (2)
三、分段函数 (4)
四、函数的图象 (5)
五、二次函数 (7)
六、指对幂函数 (7)
七、函数与方程 (8)
八、新定义题 (9)
一、函数及其表示
二、函数的基本性质
三、分段函数
四、函数的图象..
..
2023春·广东韶关·高二统考期末)
e3
cosπ
e2
x
x
x
⎫
-⎛⎫
⋅+
⎪ ⎪
+⎝⎭
⎭
部分图象大致是(
..
. .
2023春·云南楚雄·高二统考期末)函数)32e e 1
x
x x =-的部分图象大致为( )
2023春·湖北武汉·高一华中师大一附中校考期末)下列四个函数中的某个函数在区间致图象如图所示,则该函数是(
A .322x
x
x x
y --=+B .cos222x
x
x x
y -=+5.(2023春·河北沧州·高二统考期中)函数. .
. .
2023·内蒙古赤峰·统考二模)函数2
1
sin x x -
在()π,0-
A.B.
C.D.
五、二次函数
六、指对幂函数
七、函数与方程
八、新定义题A.2
=-B.
4
y x x。
专题二 函数概念与基本初等函数Ⅰ第六讲 函数综合及其应用答案部分1.A 【解析】解法一 函数()f x 的图象如图所示,当||2xy a =+的图象经过点(0,2)时,可知2a =±.当2x y a =+的图象与2y x x =+的图象相切时,由22x a x x+=+,得2240x ax -+=,由0∆=,并结合图象可得2a =,要使()||2xf x a +≥恒成立,当0a ≤时,需满足2a -≤,即20a -≤≤,当0a >时,需满足2a ≤,所以22a -≤≤.解法二 由题意0x =时,()f x 的最小值2,所以不等式()||2xf x a +≥等价于 ||22xa +≤在R 上恒成立. 当a=0x =,得|22x+>,不符合题意,排除C 、D ; 当a =-0x =,得|22x->,不符合题意,排除B ;选A .2.B 【解析】由()(2)f x f x =-知()f x 的图像关于直线1x =对称,又函数22|23||(1)4|y x x x =--=--的图像也关于直线1x =对称,所以这两个函数图像的交点也关于直线1x =对称, 不妨设12m x x x <<⋅⋅⋅<,则112mx x +=,即12m x x +=, 同理212m x x -+=,……,由121mim i xx x x ==++⋅⋅⋅+∑,所以121112()()()2mim m m i xx x x x x x m -==++++⋅⋅⋅++=∑,所以1mii xm ==∑,故选B .3.B 【解析】由已知可设2(0)()2(0)-⎧≥⎪=⎨<⎪⎩x xx f x x ,则2(0)()2(0)-⎧≥⎪=⎨<⎪⎩a a a f a a ,因为()f x 为偶函数,所以只考虑0≥a 的情况即可.若()2≤b f a ,则22≤a b,所以≤a b .故选B .4.B 【解析】因为第一次邮箱加满,所以第二次的加油量即为该段时间内的耗油量,故耗油量48V =升.而这段时间内行驶的里程数3560035000600S =-=千米.所以这段时间内,该车每100千米平均耗油量为481008600⨯=升,故选B . 5.B 【解析】采用特殊值法,若1,2,3,1,2,3x y z a b c ======,则14ax by cz ++=,10az by cx ++=,11ay bz cx ++=,13ay bx cz ++=,由此可知最低的总费用是az by cx ++.6.B 【解析】由题意可知2p at bt c =++过点(3,0.7),(4,0.8)(5,0.5),代入2p at bt c =++中可解得0.2, 1.5,2a b c =-==-, ∴220.2 1.520.2( 3.75)0.8125p t t t =-+-=--+ ∴当 3.75t =分钟时,可食用率最大.7.D 【解析】设年平均增长率为x ,原生产总值为a ,则2(1)(1)(1)p q a a x ++=+,解得1x =,故选D .8.A 【解析】解法一 由题意可知,该三次函数满足以下条件:过点(0,0),(2,0),在(0,0)处的切线方程为y = -x ,在(2,0)处的切线方程为y = 3x -6,以此对选项进行检验.A 选项,321122y x x x =--,显然过两个定点,又2312y x x '=--, 则02|1,|3x x y y ==''=-=,故条件都满足,由选择题的特点知应选A .解法二 设该三次函数为32()f x ax bx cx d =+++,则2()32f x ax bx c '=++由题设有(0)0(2)0(0)1(2)3f f f f =⎧⎪=⎪⎨'=-⎪⎪'=⎩,解得11,,1,022a b c d ==-=-=.故该函数的解析式为321122y x x x =--,选A .9.A 【解析】设所求函数解析式为()y f x =,由题意知(5)2,52f f =--=(),且(5)0f '±=,代入验证易得3131255y x x =-符合题意,故选A . 10.1[,2]8【解析】当30x -≤≤时,()||f x x ≤恒成立等价于222x x a x ++--≤恒成立,即232a x x --+≤恒成立,所以2min (32)2a x x --+=≤; 当0x >时()||f x x ≤恒成立等价于222x x a x -+-≤恒成立,即22x x a -+≥恒成立,所以2max 1()28x x a -+=≥.综上,a 的取值范围是1[,2]8.11.36π【解析】取SC 的中点O ,连接,OA OB ,因为,SA AC SB BC ==,所以,OA SC OB SC ⊥⊥. 因为平面SAC ⊥平面SBC ,所以OA ⊥平面SBC . 设OA r =,3111123323A SBC SBC V S OA r r r r -∆=⨯⨯=⨯⨯⨯⨯=所以31933r r =⇒=,所以球的表面积为2436r ππ=.12.1[,1]2【解析】由题意,22222(1)221u x y x x x x =+=+-=-+,且[0,1]x ∈,又0x =时,221u x y =+=,12x =时,2212u x y =+=,当1x =时,221u x y =+=,所以22x y +取值范围为1[,1]2.1322221145+28=4833r r r ππππ⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯⇒.14.)+∞【解析】函数()g x 的定义域为[1,2]-,根据已知得()()()2h x g x f x +=,所以()=2()()62h x f x g x x b -=+-()()h x g x >恒成立,即62x b +>令3y x b =+,y =,则只要直线3y x b=+在半圆224(0)x y y +=≥2>,解得b >,故实数b 的取值范围是)+∞.15.160【解析】设该容器的总造价为y 元,长方体的底面矩形的长x m ,因为无盖长方体的容积为34m ,高为1m ,所以长方体的底面矩形的宽为4m x,依题意,得24420410(2)8020()8020160y x x x x ⨯=⨯++=+++⨯=≥. 16.①③④【解析】对于①,根据题中定义,()A f x ∈⇔函数()y f x =,x D ∈的值域为R ,由函数值域的概念知,函数()y f x =,x D ∈的值域为,R b R a D ⇔∀∈∃∈()f a b =,所以①正确;对于②,例如函数||1()()2x f x =的值域(0,1]包含于区间[1,1]-,所以()f x B ∈,但()f x 有最大值l ,没有最小值,所以②错误;对于③,若()()f x g x B +∈,则存在一个正数1M ,使得函数()()f x g x B +∈的值域包含于区间11[,]M M -,所以1M -≤()f x 1()g x M +≤,由()g x B ∈知,存在一个正数2M ,使得函数()g x 的值域包含于区间22[,]M M -,所以22()M g x M -≤≤,亦有22()M g x M -≤-≤,两式相加得12()M M -+≤()f x ≤12M M +,于是()f x B ∈,与已知“.()f x A ∈”矛盾,故()()f x g x B +∉,即③正确;对于④,如果0a >,那么,()x f x →+∞→+∞,如果0a <,那么2,()x f x →-→+∞,所以()f x 有最大值,必须0a =,此时2()1x f x x =+在区间(2,)-+∞上,有11()22f x -≤≤,所以()f x B ∈,即④正确,故填①③④.17.【解析】(1)当030x <≤时,()3040f x =<恒成立,公交群体的人均通勤时间不可能少于自驾群体的人均通勤时间;当30100x <<时,若40()f x <,即180029040x x+->,解得20x <(舍)或45x >; ∴当45100x <<时,公交群体的人均通勤时间少于自驾群体的人均通勤时间; (2)设该地上班族总人数为n ,则自驾人数为%n x ⋅,乘公交人数为(1%)n x ⋅-.因此人均通勤时间30%40(1%),030()1800(290)%40(1%),30100n x n x x ng x x n x n x x x n ⋅⋅+⋅⋅-⎧<⎪⎪=⎨+-⋅⋅+⋅⋅-⎪<<⎪⎩≤,整理得:240,0010()1(32.5)36.875,3010050x x g x x x ⎧-<⎪⎪=⎨⎪-+<<⎪⎩≤3,则当(0,30](30,32.5]x ∈,即(0,32.5]x ∈时,()g x 单调递减;当(32.5,100)x ∈时,()g x 单调递增.实际意义:当有32.5%的上班族采用自驾方式时,上班族整体的人均通勤时间最短. 适当的增加自驾比例,可以充分的利用道路交通,实现整体效率提升;但自驾人数过多,则容易导致交通拥堵,使得整体效率下降.18.【解析】(1)由题意知,点M ,N 的坐标分别为()5,40,()20,2.5.将其分别代入2a y xb =+,得4025 2.5400aba b⎧=⎪⎪+⎨⎪=⎪+⎩,解得10000a b =⎧⎨=⎩. (2)①由(1)知,21000y x =(520x ≤≤),则点P 的坐标为21000,t t ⎛⎫ ⎪⎝⎭, 设在点P 处的切线l 交x ,y 轴分别于A ,B 点,32000y x'=-, 则l 的方程为()2310002000y x t t t -=--,由此得3,02t Α⎛⎫ ⎪⎝⎭,230000,Βt ⎛⎫⎪⎝⎭.故()f t ==,[]5,20t ∈.②设()624410g t t t ⨯=+,则()6516102g t t t⨯'=-.令()0g t '=,解得t =当(t ∈时,()0g t '<,()g t 是减函数;当()20t ∈时,()0g t '>,()g t 是增函数.从而,当t =()g t 有极小值,也是最小值,所以()min 300g t =, 此时()min f t =答:当t =l的长度最短,最短长度为19.【解析】(Ⅰ)因为蓄水池侧面积的总成本为1002200rh rh ππ⋅=元,底面的总成本为2160r π元,所以蓄水池的总成本为(2200160rh r ππ+)元.又题意据220016012000rh r πππ+=,所以21(3004)5h r r=-, 从而23()(3004)5V r r h r r ππ==-.因0r >,又由0h >可得r <故函数()V r的定义域为. (Ⅱ)因3()(3004)5V r r r π=-,故2()(30012)5V r r π'=-.令()0V r '=,解得125,5r r ==-(因25r =-不在定义域内,舍去). 当(0,5)r ∈时,()0V r '>,故()V r 在(0,5)上为增函数;当r ∈时,()0V r '<,故()V r在上为减函数. 由此可知,()V r 在5r =处取得最大值,此时8h =. 即当5r =,8h =时,该蓄水池的体积最大.20.【解析】(1)当1,1,2b c n ==-…时,()1nf x x x =+-.∵111()(1)()10222nf f =-⨯<,∴()f x 在1(,1)2内存在零点. 又当1(,1)2x ∈时,1()10n f x nx -'=+>,∴()f x 在1(,1)2上是单调递增的,∴()f x 在区间1(,1)2内存在唯一的零点;(2)解法一 由题意知1(1)1,1(1)1,f f --⎧⎨-⎩剟剟即02,20,b c b c -⎧⎨-+⎩剟剟由图像知,3b c +在点(0,2)-取得最小值6-,在点(0,0)取得最大值0.b解法二 由题意知1(1)11f b c-=++剟,即20b c -+剟.…①1(1)11f b c --=-+剟,即20b c --+?-?.…② ①2⨯+②得62()()30b c b c b c -++-+=+?-?, 当0,2b c ==-时,36b c +=-;当0b c ==时,30b c +=. 所以3b c +的最小值6-,最大值0. 解法三 由题意知(1)1,(1)1,f b c f b c -=-+⎧⎨=++⎩,解得(1)(1)(1)(1)2,22f f f f b c --+--==,32(1)(1)3b c f f +=+--.又∵1(1)1,1(1)1,f f --⎧⎨-⎩剟剟,∴630b c -+??.当0,2b c ==-时,36b c +=-;当0b c ==时,30b c +=. 所以3b c +的最小值6-,最大值0. (3)当2n =时,2()f x x bx c =++.对任意12,x x [1,1]∈-都有有12()()4f x f x -…等价于()f x 在[-1,1]上的最大值与最小值之差4M ….据此分类讨论如下: (ⅰ)当12b>,即2b >时, (1)(1)24M f f b =--=>,与题设矛盾. (ⅱ)当102b --<…,即02b <…时, 2(1)()(1)422b bM f f =--=+…恒成立.(ⅲ) 当012b-<…,即20b -剟时, 2(1)()(1)422b bM f f =---=-…恒成立.综上可知,22b-剟.21.【解析】设包装盒的高为h (cm ),底面边长为a (cm ),由已知得.300),30(22260,2<<-=-==x x xh x a(1),1800)15(8)30(842+--=-==x x x ah S 所以当15=x 时,S 取得最大值.(2)).20(26),30(22222x x V x x h a V -='+-==由00=='x V 得(舍)或x =20.当)20,0(∈x 时,0V '>;(20,30)0x V '∈<当时. 所以当x =20时,V 取得极大值,也是最小值. 此时12h a =,即装盒的高与底面边长的比值为12.。