重庆市梁平实验中学高中数学+第一章+三角函数复习(一)教案+新人教A版必修四

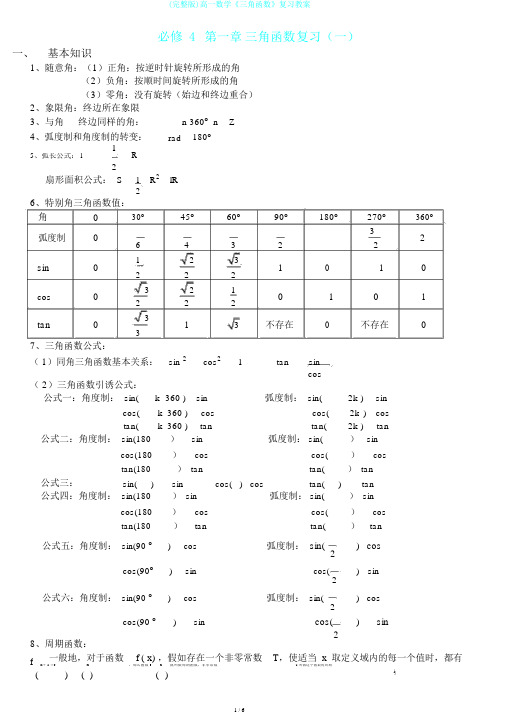
必修 4 第一章 三角函数 复习（一）一、 基本知识1、随意角：（1）正角：按逆时针旋转所形成的角（2）负角：按顺时间旋转所形成的角（3）零角：没有旋转（始边和终边重合） 2、象限角：终边所在象限 3、与角 终边同样的角： n 360o n Z 4、弧度制和角度制的转变：rad180o1R5、弧长公式： l21 扇形面积公式： SR 2 lR26、特别角三角函数值：角 0 30o45o60o90o 180o270o 360o弧度制3 2 643 22sin1 23 10 1 0222cos3 21 011 222tan31 3不存在不存在37、三角函数公式：（ 1）同角三角函数基本关系： sin 2cos 21tansin （ 2）三角函数引诱公式：cos公式一：角度制： sin(k 360 ) sin弧度制： sin(2k ) sincos( k 360 ) cos cos( 2k ) costan( k 360 ) tantan(2k ) tan公式二：角度制： sin(180 ） sin弧度制： sin(） sin cos(180 ）coscos( ）costan(180） tantan(） tan 公式三： sin( ) sincos( ) costan()tan公式四：角度制： sin(180） sin 弧度制： sin(） sin cos(180 ） cos cos(）costan(180） tantan(） tan 公式五：角度制： sin(90 o)cos 弧度制： sin(2) coscos(90o)sincos(2) sin公式六：角度制： sin(90 o)cos弧度制： sin(2) coscos(90 o)sincos()sin8、周期函数：2f一般地，对于函数 f ( x) ，假如存在一个非零常数 T ，使适当 x 取定义域内的每一个值时，都有( x ＋ T ＝fx ，那么函数 f ( x 就叫做周期函数，非零常数 T 叫做这个函数的周期) ( ))9、正弦函数： y=sinx（ 1）定义域： R 值域： [-1,1]（ 2）图象：五点法绘图正弦函数 y=sinx ，x∈[0 ， 2π ] 的图象中，五个重点点是： (0,0) (,1) (,0) (3,-1) (2 ,0)22（ 3）周期性： 2kπ (k ∈Z 且 k≠ 0) 都是它的周期，最小正周期是2π（4）奇偶性：正弦函数在定义域 R 内为奇函数，图象对于原点对称（5）单一性：在［－2＋ 2kπ，2＋2kπ］( k∈ Z) 上都是增函数；3在［2＋2kπ，2＋2kπ］( k∈ Z) 上都是减函数。

高中数学 第1章 三角函数复习与小结教案 新人教版必修4 教学目标：1．进一步巩固三角函数的图象、性质；2．应用三角函数解决实际问题；3．渗透数形结合与转化思想．教学重点：让学生掌握三角函数的图象；熟练运用三角公式．教学难点：图象变换．教学过程：一、问题情景问题：本章有哪些知识点？1．任意角的概念；2．角度制与弧度制；3．任意角的三角函数；4．三角函数的图象与性质；二、学生活动1．sin390°＋cos120°＋sin225°的值是 ．2．︒-︒︒-︒23cos 37cos 23sin 37sin ＝ ． 3．已知sin θ＋cos θ＝51-，(0,),πθ∈ tan θ的值是 ． 4．关于函数f (x )＝4sin(2x ＋π3)(x ∈R)，有下列命题： （1）y ＝f (x )的表达式可改写为y ＝4·cos(2x －π6)； （2）y ＝f (x )是以2π为最小正周期的周期函数；（3）y ＝f (x )的图象关于点（－π6，0）对称； （4）y ＝f (x )的图象关于直线x ＝－π6对称．其中正确的命题序号是 （注：把你认为正确的命题序号都填上）．三、数学应用1．例题：例1 已知角α终边上一点0),3,4(≠-a a a P ，求)29sin()211cos()sin()2cos(απαπαπαπ+---+的值． 分析 利用三角函数的定义，以及诱导公式．例2 已知函数cos 2(0)6y a b x b π=-+>⎛⎫ ⎪⎝⎭的最大值为23，最小值为21-. （1）求b a ,的值；（2）求函数)3sin(4)(π--=bx a x g 的最小值并求出对应x 的集合.分析：（1）利用三角函数的性质，]1,1[)62cos(-∈+πx （2）利用三角函数的性质，]1,1[)3sin(-∈-πbx 2．练习：（1）函数)22cos(π+=x y 的图象的对称轴方程是 ；（2）要得到函数y ＝sin(2x -3π)的图象，只要将函数y ＝sin2x 的图象 ； （3）已知()sin()cos()4f x a x b x παπβ=++++（,,,a b αβ为非零实数），(2007)5f =，则(2008)f = ；（4）函数)32cos(π--=x y 的单调递增区间是 ． 四、要点归纳与方法小结1．进一步巩固、熟悉了三角函数的图象、性质并加以灵活应用；2．初步学会了如何应用三角函数解决实际问题；3．进一步渗透了数形结合与转化思想．。

第一章三角函数复习(一)教学目的【过程与方法】一、知识结构：二、知识要点：1. 角的概念的推广：(1) 正角、负角、零角的概念：(2) 终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合：}Z ,360|{∈+︒⋅==k k S αββ① 象限角的集合：第一象限角集合为： ；第二象限角集合为： ；第三象限角集合为： ；第四象限角集合为： ；② 轴线角的集合：终边在x 轴非负半轴角的集合为： ；终边在x 轴非正半轴角的集合为： ；故终边在x 轴上角的集合为： ；终边在y 轴非负半轴角的集合为： ；终边在y 轴非正半轴角的集合为： ；故终边在y 轴上角的集合为： ；终边在坐标轴上的角的集合为： .2. 弧度制： 我们规定，长度等于半径的弧所对的圆心角叫做1弧度的角；用弧度来度量角的单位制叫做弧度制. 在弧度制下，1弧度记做1rad.(1) 角度与弧度之间的转换：① 将角度化为弧度：π2360=︒ π=︒180rad 01745.01801≈=︒π rad n n 180π=︒② 将弧度化为角度： ︒=3602π ︒=180π 815730.57)180(1'︒=︒≈︒=πrad ︒=) 180(πn n 任意角与弧度制：单位圆任意角的三角函数三角函数线；三角函数的图象和性质三角函数线模型的简单应用同角三角函数的基本关系式诱导公式(2) 把上述象限角和轴线角用弧度表示.(3) 上述象限角和轴线角用弧度表示：; α⋅=r l 弧长公式：. 21lR S =扇形面积公式：3. 任意角的三角函数：.0 ),( (1)22>+=y x r y x P 是它与原点的距离，的坐标是其终边上任意一点是一个任意大小的角，设α ①;sin sin r y r y =ααα，即的正弦，记作叫做比值 ②;cos cos r x r x =ααα，即的余弦，记作叫做比值 ③.tan tan x y x y =ααα，即的正切，记作叫做比值 (2) 判断各三角函数在各象限的符号：(3) 三角函数线：4. 同角三角函数基本关系式：(1) 平方关系： 1cos sin 22=+αα(2) 商数关系：αααcos sin tan =5. 诱导公式诱导公式(一) )Z (tan )2tan()Z (cos )2cos()Z (sin )2sin(∈=+∈=+∈=+k k k k k k ααπααπααπ诱导公式(二)tan )tan(cos )cos(sin )sin(ααπααπααπ=+-=+-=+诱导公式(三)tan )tan(cos )cos(sin )sin(αααααα-=-=--=-诱导公式(四)sin(π－α)=sin αcos(π －α)=－cos αtan (π－α)=－tan α诱导公式(五)ααπααπααπtan )2tan(cos )2cos(sin )2sin(-=-=--=-对于五组诱导公式的理解 ：可以是任意角；公式中的α .1. 360,180, 180 , , )Z ( 360 .2符号看成锐角时原函数值的前面加上一个把它的同名三角函数值，于等的三角函数值，括为：这五组诱导公式可以概αααααα-︒-︒+︒-∈+︒⋅k k 函数名不变，符号看象限3.利用诱导公式将任意角三角函数转化为锐角三角函数的基本步骤：三、基础训练：) ( sin ],2,[,23)(cos .1的值为则且已知αππααπ∈=+23 D. 21 C. 21- B. 21 A.±±23 D. 23 C. 21- B. 21 A.) ( )647(-cos .2-的值为π.__________)3cos(,tan )3tan(,101-)sin(3 .3=--=-=+παααπαπ则且若. _______)tan()cos(-)sin( .4=--⋅+απααπ化简：诱导公式二或四或五诱导公式三或一任意负角的三角函数任意正角的三角函数0o 到360o 角的三角函数锐角的三角函数诱导公式一) (cot tan ,32cos sin .5的值是则已知θθθθ+=+518- D. 45 C. 49 B. 185 A.. _____cos sin ,83cos sin .6=+=⋅ααααα是第三象限角，则且已知 四、典型例题：.),360,360(),2,2()2( _____630(1) 1.中绝对值最小的角，并求出的集合试写出角并且的终边经过点若角象限角；是第角，则后成为角边在按顺时针方向旋转是第二象限角，当其终若例A A P αααααθ︒︒-∈-︒. ,30 125 (2) ___,43tan ___,34cos ___,3sin 2.(1)2求扇形的弧长和半径长弧度，面积为已知扇形的圆心角为计算：例cm πππππ===例3. 化简：设Z,∈k .])1cos[(])1sin[()cos()sin(απαπαπαπ-++++-k k k k 五、课堂小结1. 任意角的三角函数；2. 同角三角函数的关系；3. 诱导公式.六、课后作业阅读教材P.67-P.68；《习案》作业十六中1至6题.精美句子1、善思则能“从无字句处读书”。

第一章《三角函数》教学设计（复习课）【教学目标】１．任意角的概念与弧度制；任意角三角函数（正弦、余弦、正切）的定义； 2．同角三角函数的关系（22sin cos 1x x +=，sin tan cos xx x=），诱导公式； 3．正弦、余弦、正切函数的图象与性质；4．利用三角函数的图象求三角函数的定义域、值域等；5．函数sin()y A x ωϕ=+的实际意义；函数sin()y A x ωϕ=+图象的变换（平移平换与伸缩变换）；6.会用三角函数解决一些简单实际问题及最值问题. 【导入新课】 复习回顾本章知识 新授课阶段一、同角三角函数基本关系式的运用 例1若tan α=，求：（1）sin cos cos sin αααα+-的值；（2）222sin sin cos cos αααα-+的值． 解：（1）cos sin 1tan 3cos sin 1tan αααααα++===----（2）原式2222222sin sin cos cos 2tan tan 1sin cos tan 1ααααααααα-+-+==++41533-==. 例2 若1sin cos ,,,cos sin 842ππθθθθθ⎛⎫=∈- ⎪⎝⎭求的值． 解：222(cos sin )cos sin 2sin cos θθθθθθ-=+-13144=-=，,,cos sin .42cos sin ππθθθθθ⎛⎫∈∴< ⎪⎝⎭∴-=例3 已知sin()cos(2)tan(3)2()tan()sin()2f παπααπαππαα---+=++．（1） 化简()f α；（2） 若α是第三象限的角，且31cos()25πα-=，求()f α的值； （3） 若01860α=-，求()f α的值．解：（1）cos cos (tan )()cos tan cos f ααααααα-==-.（2）3cos()sin 2παα-=-，1sin ,5αα∴=-又是第三象限的角.()f αα∴==∴=cos . （3）0186********α=-=-⨯+，00()(1860)cos(1860)f f α∴=-=--0001cos(6360300)cos602=--⨯+=-=-.二、正弦函数、余弦函数的图象与性质的应用 例4求下列函数的定义域： （1）()f x =（2）()tan(sin )f x x =；（3）()lg(tan 1)f x x =+．解：（1tan 0x ≥，得tan x ≤()23k x k k Z ππππ-<≤+∈．∴()f x 的定义域为(,]()23k k k Z ππππ-+∈．（2）∵1sin 122x ππ-<-≤≤<，∴x R ∈．即()f x 的定义域为R ．（3）由已知2cos 10,lg(tan 1)0,tan 10,(Z),2x x x x k k ππ-≥⎧⎪+≠⎪⎪⎨+>⎪⎪≠+∈⎪⎩得1cos ,2tan 0,tan 1,(Z).2x x x x k k ππ⎧≥⎪⎪≠⎪⎨>-⎪⎪≠+∈⎪⎩∴22,33,.42k x k x k k x k πππππππππ⎧-≤≤+⎪⎪≠⎨⎪⎪-<<+⎩(Z)k ∈ ∴原函数的定义域为(2,2)(2,2)(Z)43k k k k k ππππππ-+∈．例5求下列函数的周期：（1）sin 2sin(2)3cos 2cos(2)3x x y x x ππ++=++；（2）2sin()sin 2y x x π=-；（3）cos 4sin 4cos 4sin 4x x y x x +=-．解：（1）1)sin 2sin 2cos 26tan(2)6)6x x x xy x x πππ+++===++， ∴周期2T π=．（2）2sin cos sin 2y x x x =-=-，故周期T π=． （3）1tan 4tan(4)1tan 44x y x x π+==+-，故周期4T π=．例6已知函数f(x)=3sin(2x －π6)+2sin 2(x －π12) (x∈R)．(1)求函数f (x )的最小正周期； (2)求使函数f(x )取得最大值的x 的集合． 解:(1) f (x )=3sin(2x －π6)+1－cos2(x －π12)= 2[32sin2(x －π12)－12 cos2(x －π12)]+1 =2sin[2(x －π12)－π6]+1=2sin(2x －π3)+1，∴ T=2π2=π.(2)当f(x)取最大值时, sin(2x －π3)=1,有2x －π3 =2k π+π2.即x=k π+ 5π12 (k∈Z).∴所求x 的集合为{x∈R|x= kπ+ 5π12,k∈Z}.例7判断下列函数的奇偶性：（１）()sin 2tan f x x x =-； (2 ) 1sin cos ()1sin cos x xf x x x+-=++；(3 ) ()cos(sin )f x x =； (4 ) ()f x = 解：（1）()f x 的定义域为()2x k k Z ππ≠+∈，故其定义域关于原点对称，又()sin(2)tan()sin 2tan ()f x x x x x f x -=---=-+=-，()f x ∴为奇函数.（2）2x π=时，1sin cos 2x x ++=，而1sin cos 02x x x π=-++=时,，()f x ∴的定义域不关于原点对称，()f x ∴为非奇非偶函数.（3）()f x 的定义域为R ，又()cos(sin())cos(sin )()f x x x f x -=-==，()f x ∴为偶函数.（4）由lgcos 0x ≥得cos 1x ≥，又cos 1x ≤cos 1x ∴=，故此函数的定义域为2()x k k Z π=∈，关于原点对称，此时()0.f x = ()f x ∴既是奇函数，又是偶函数.例8已知:函数()()x x x f cos sin log 21-=．(1)求它的定义域和值域； (2)判断它的奇偶性； (3)求它的单调区间； （4）判断它的周期性,若是周期函数,求它的最小正周期.解:(1).由0cos sin >-x x 04sin 2>⎪⎭⎫ ⎝⎛-⇒πx ，ππππ+<-<∴k x k 242(Z)k ∈.∴定义域为()52,2Z .44k k k ππππ⎛⎫++∈ ⎪⎝⎭(]2,04sin 2∈⎪⎭⎫ ⎝⎛-πx ，∴值域为.,21⎪⎭⎫⎢⎣⎡+∞-(2) 定义域不关于原点对称,∴函数为非奇非偶函数.（3） sin cos 04x x x π⎛⎫-=-> ⎪⎝⎭，()f x ∴的递增区间为35[2,2)(Z)44k k k ππππ++∈， 递减区间为3(2,2]()44k k k Z ππππ++∈.(4)()()()122log sin 2cos 2f x x x πππ+=+-+⎡⎤⎣⎦()12log sin cos x x =-()f x =，()f x ∴是周期函数,最小正周期T π2=.例9已知函数22()sin 2sin cos 3cos f x x x x x =++，x R ∈．求: (I)函数()f x 的最大值及取得最大值的自变量x 的集合； (II) 函数()f x 的单调增区间． 解：(I)1cos 23(1cos 2)()sin 21sin 2cos 22),224x x f x x x x x π-+=++=++=+∴当2242x k πππ+=+,即()8x k k Z ππ=+∈时, ()f x 取得最大值2函数()f x 的取得最大值的自变量x 的集合为{/,()}8x x R x k k Z ππ∈=+∈.(II) ()2)4f x x π=++.由题意得: 222()242k x k k Z πππππ-≤+≤+∈，即: 3()88k x k k Z ππππ-≤≤+∈. 因此函数()f x 的单调增区间为3[,]()88k k k Z ππππ-+∈.三、函数sin()y A x ωϕ=+的图象与变换例10已知函数2()2cos 2,(01)f x x x ωωω=+<<其中，若直线3x π=为其一条对称轴.（1）试求ω的值；（2）作出函数()f x 在区间[,]ππ-上的图象．解：（1）2()2cos 21cos 22f x x x x x ωωωω=+=+2sin(2)16x πω=++.3x π=是()y f x =的一条对称轴，2sin()136ωππ∴+=±. 2,,362k k Z ωππππ∴+=+∈13()22k k Z ω∴=+∈.101,.2ωω<<∴=（2）用五点作图例11 已知函数2()sin ()(0,0,0)2f x A x A πωϕωϕ=+>><<，且()y f x =的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1,2）．（I ）求ϕ；（II ）计算(1)(2)(2008)f f f +++．解：（I ）2sin ()cos(22).22A Ay A x x ωϕωϕ=+=-+()y f x =的最大值为2，0A >.2, 2.22A AA ∴+==又其图象相邻两对称轴间的距离为2，0ω>，12()2,.224ππωω∴== 22()cos(2)1cos(2)2222f x x x ππϕϕ∴=-+=-+.()y f x =过(1,2)点，cos(2) 1.2πϕ∴+=-22,,2k k Z πϕππ∴+=+∈22,,2k k Z πϕπ∴=+∈ ,,4k k Z πϕπ∴=+∈又0,2πϕ<<4πϕ∴=.（II ）4πϕ=，1cos()1sin .222y x x πππ∴=-+=+(1)(2)(3)(4)21014f f f f ∴+++=+++=.又()y f x =的周期为4，20084502=⨯，(1)(2)(2008)45022008.f f f ∴++⋅⋅⋅+=⨯=例12设函数2()sin cos f x x x x a ωωω=++（其中0,a R ω>∈）.且()f x 的图像在y 轴右侧的第一个最高点的横坐标是6π． （Ⅰ）求ω的值；（Ⅱ）如果()f x 在区间5[,]36ππ-，求a 的值．解：（I ）1()cos 2sin 2sin(2)22232f x x x x a πωωαω=+++=+++ 依题意得 126322πππωω⋅+=⇒=．（II ）由（I ）知，3()sin()32f x x πα=+++．又当5[,]36x ππ∈-时， 7[0,]36x ππ+∈，故1sin()123x π-≤+≤，从而()f x 在区间π5π36⎡⎤-⎢⎥⎣⎦，上的最小值为13322a =-++，故31.2a +=四、三角函数的运用例13某港口水的深度y （米）是时间240(≤≤t t ，单位：时）的函数，记作)(t f y =，下面是某日水深的数据：经长期观察，)(t f y =的曲线可以近似地看成函数sin y A x b ω=+的图象. （1）试根据以上数据，求出函数)(t f y =的近似表达式，（2）一般情况下船舶航行时，船底离海底的距离为5米或5米以上时认为是安全的（船舶停靠时，船底只需不碰海底即可）.某船吃水深度（船底离水面的距离）为，如果该船希望在同一天内安全进出港，请问，它至多能在港内停留多长时间（忽略进出港所需时间）？解：（1）由已知数据，易知函数)(t f y =的周期T=12，振幅A=3，b=10，3sin106y t π∴=+.13sin1011.5,sin662t t ππ∴+≥∴≥,解得:)(652662Z k k t k ∈+≤≤+πππππ. )(512112Z k k t k ∈+≤≤+,在同一天内,取1713,5110≤≤≤≤∴==t t k k 或或.∴该船可在当日凌晨1时进港,下午17时出港,在港口内最多停留16个小时. 例14如图所示，一个摩天轮半径为10米，轮子的底部在地面上2米处，如果此摩天轮每20秒转一圈，且当摩天轮上某人经过点P 处（点P 与摩天轮中心Ｏ高度相同）时开始计时，（1） 求此人相对于地面的高度关于时间的函数关系式；t 时 0 3 6 9 12 15 18 21 24 y 米（2） 在摩天轮转动的一圈内，有多长时间此人相对于 地面的高度不超过10米？解：（1）以Ｏ为坐标原点，以OP 所在直线为x 轴建立如图所示的平面直角坐标系，设摩天轮上某人在Q 处，则在t 秒内OQ 转过的角为220t π，所以t 秒时，Q 点的纵坐标为220t π，故在t 秒时此人相对于地面的高度为10sin1210y t π=+（米）.（2）令10sin121210y t π=+≤，则1sin105t π≤-. 020,t ≤≤10.6419.36t ∴≤≤地面的高度不超过10米.例15 如图,ABCD 是一块边长为100米的正方形地皮，其中ATPS 是一半径为90米的扇形小山，P 是弧TS 上一点，其余部分都是平地，现一开发商想在平地上建造一个有边落在BC 与CD 上的长方形停车场PQCR ，求长方形停车场的最大值与最小值.解：如图，连结AP ，设0(090)PAB θθ∠=<<，延长RP 交AB 于M ， 则90cos ,90sin AM MP θθ==，10090cos PQ MB AB AM θ==-=-，10090sin PR MR MP θ=-=-，故矩形PQCR 的面积(10090cos )(10090sin )S PQ PR θθ=⋅=-- 100009000(sin cos )8100sin cos θθθθ=-++.设21sin cos (12),sin cos (1)2t t t θθθθ+=<≤=-则，2810010()95029S t ∴=-+，故当109t =时，2min 950()S m =.当2t =时，2max 1405090002()S m =-.例16．将一块圆心角为1200，半径为20㎝的扇形铁片裁成一块矩形，有如图(1)、(2)的两种裁法：让矩形一边在扇形的一条半径OA 上，或让矩形一边与弦AB 平行，请问哪种裁法能得到最大面积的矩形？并求出这个最大值.解：按图(1)的裁法：矩形的一边OP 在OA 上，顶点M 在圆弧上，设MOA θ∠=，则20sin ,20cos MP OP θθ==，所以矩形OPMN 的面积400sin cos 200sin 2,S θθθ==即当4πθ=时，max 200S =.按图(2)的裁法：矩形一边PQ 与弦AB 平行，设MOQ α∠=，在△MOQ 中，0009030120OQM ∠=+=，则正弦定理得：020sin sin sin1203MQ αα==. 又002sin(60)40sin(60)MN OM αα=-=-，0sin(60)3S MQ MN αα∴=⋅=-1(sin )322ααα=-1cos 2(2)344αα-=-030)33α=+-.∴ 当030α=时，max S =200>2cm .课堂小结主要掌握正弦函数与余弦函数的图象与性质，这是本章的核心知识点，主要的思想方法就是数形结合思想和分类讨论思想.作业 见同步练习 拓展提升1．34sin ,cos ,255θθθ=-=若则角的终边在 （ ） A ．第一象限 B ．第二象限 Ｃ．第三象限 Ｄ．第四象限２．已知sin 1,cos 43k k θθ=-=-，且θ是第二象限角，则k 应满足的条件是( )A ．43k >Ｂ．1k = Ｃ．85k = Ｄ．1k > ３．已知1sin 1cos ,cos 2sin 1x xx x +=--那么的值是 （ ） A ．12 B ．12- Ｃ．２ Ｄ．－２4. 给出四个函数，则同时具有以下两个性质的函数是：①最小正周期是π；②图象关于点（6π，0）对称 （ ） （A ）)62cos(π-=x y （B ）)62sin(π+=x y （C ）)62sin(π+=x y （D ）)3tan(π+=x y5．为了使函数)0(sin >=ωωx y 在区间[0，1]上至少出现50次最大值，则ω的最小值是（ ）（A ）π98 （B ）π2197 （C ）π2199（D ）π100 f （x ）=cos 2x +sin x 在区间［－4π，4π］上的最小值是 （ ） A.212- B.－221+ C.－1 D.221- 7．函数f (x )=sin(2x+φ)+3cos(2x +φ)的图像关于原点对称的充要条件是 （ ） A ．φ=2k π－π6 ，k ∈Z B ．φ=k π－π6 ，k ∈ZC ．φ=2k π－π3 ，k ∈ZD ．φ=k π－π3 ，k ∈Z8．在ABC ∆中，2π>C ，若函数)(x f y =在[0，1]上为单调递减函数，则下列命题正确的是（A ）)(cos )(cos B f A f > （B ）)(sin )(sin B f A f > （C ）)(cos )(sin B f A f > （D ）)(cos )(sin B f A f <9.同时具有性质“⑴ 最小正周期是π；⑵ 图象关于直线3x π=对称；⑶ 在[,]63ππ-上是增函数”的一个函数是( )A ．)62sin(π+=x y B.)32cos(π+=x yC ．)62cos(π-=x y D.)62sin(π-=x y 10．若把一个函数的图象按a =（3π-，－2）平移后得到函数x y cos =的图象，则原图象的函数解析式是 （ ）（A ）2)3cos(-+=πx y （B ）2)3cos(--=πx y（C ）2)3cos(++=πx y （D ）2)3cos(+-=πx y11．为了得到函数y =sin （2x －6π）的图象，可以将函数y =cos2x 的图象 （ ） 6π3π个单位长度 6π3π个单位长度12．若函数f （x ）=sin （ωx +ϕ）的图象（部分）如下图所示，则ω和ϕ的取值是 （ ）A.ω=1，ϕ=3π B.ω=1，ϕ=－3π C.ω=21，ϕ=6π D.ω=21，ϕ=－6π 13．若函数()f x 图象上每一个点的纵坐标保持不变，横坐标伸长到原来的两倍，然后再将整个图象沿x 轴向右平移2π个单位，向下平移3个单位，恰好得到1sin 2y x =的图象，则()f x =．14．函数sin(),(0,0)y A x A ωϕω=+>>为奇函数的充要条件是；为偶函数的充要条件是．15．一正弦曲线的一个最高点为1(,3)4，从相邻的最低点到这最高点的图象交x 轴于1(,0)4-，最低点的纵坐标为-3,则这一正弦曲线的解析式为. 16．已知方程sin x +cos x =k 在0≤x ≤π上有两解，求k 的取值X 围.17．数)2||,0,0(),sin(π<ϕ>ω>ϕ+ω=A x A y 的最小值是-2，其图象相邻最高点与最低点横坐标差是3π，又图象过点(0,1)，求函数解析式.18．已知函数f （x ）=A sin ωx +B cos ωx （A 、B 、ω是实常数，ω＞0）的最小正周期为2，并当x =31时，2)(max =x f .（1）求f （x ）. （2）在闭区间［421，423］上是否存在f （x ）的对称轴?如果存在，求出其对称轴方程；如果不存在，请说明理由.参考答案1．Ｄ 提示；由24sin 22sin cos 0,25θθθ==-< 227cos 2cos sin 025θθθ=-=>可得 2．Ｃ 提示：由22sin 0,cos 0sin cos 1θθθθ><+=及可得．3．Ａ 提示：221sin sin 1sin 11cos cos cos x x x x x x+--⋅==- 4．D 5．B 提示:4941×T ≤1，即4197×ωπ2≤1，∴ω≥2π197. 6．提示：f （x ）=1－sin 2x +sin x =－（sin x －21）2+45，当x =－4π时，()f x 取最小值7．D 提示：()sin(2))2sin(2)3f x x x x πϕϕϕ=++=++令3k πϕπ+=可得8．C 提示：根据00222A B A B πππ<+<<<-<,得，所以sin sin()cos 2A B B π<-=9．D 提示：由性质(1)和(2)可排除 A 和C ,再求出)62sin(π-=x y 的增区间即可10．D 提示：将函数x y cos =的图象按a -平移可得原图象的函数解析式 11．B 提示：∵y =sin （2x －6π）=cos ［2π－（2x －6π）］=cos （3π2－2x ）=cos （2x －3π2）=cos ［2（x －3π）］，∴将函数y =cos2x 的图象向右平移3π个单位长度 12．C 提示：由图象知，T =4（3π2+3π）=4π=ωπ2，∴ω=21.又当x =3π2时，y =1， sin （21×3π2+ϕ）=1，3π+ϕ=2k π+2π，k ∈Z ，当k =0时，ϕ=6π. 13．()f x =11sin(2)3cos 23222x x π++=+ 14．()k k Z ϕπ=∈ ；()2k k Z πϕπ=+∈15．3sin()4y x ππ=+16解：原方程sinx+cosx=k ⇔2sin （x+4π）=k ，在同一坐标系内作函数y 1=2sin （x+4π）与y 2=k 的图象.对于y=2sin （x+4π），令x=0，得y=1. ∴当k∈［1，2在［0，π］上有两交点，方程有两解 17．解：易知：A = 2，半周期π=32T ，∴T = 6π，即π=ωπ62，从而：31=ω. 设：)31sin(2ϕ+=x y ，令x = 0，有1sin 2=ϕ.又：2||π<ϕ，∴6π=ϕ. ∴所求函数解析式为)631sin(2π+=x y 18．解：（1）由22,T πωπω===得，()sin cos f x A x B x ππ∴=+. 由题意可得sin cos 2,332.A B ππ⎧+=⎪= 解得 1.A B ⎧=⎪⎨=⎪⎩()cos 2sin()6f x x x x ππππ∴=+=+.（2）令,62x k k Z ππππ+=+∈，所以1,3x k k Z =+∈.由21123434k ≤+≤ 得 59651212k ≤≤，5k ∴=. 所以在［421，423］上只有f （x ）的一条对称轴x =316。

新编人教版精品教学资料第一章三角函数复习(一)教学目的【过程与方法】一、知识结构：(1) 正角、负角、零角的概念：(2) 终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合：}Z ,360|{∈+︒⋅==k k S αββ ① 象限角的集合：第一象限角集合为： ；第二象限角集合为： ；第三象限角集合为： ；第四象限角集合为： ；② 轴线角的集合：终边在x 轴非负半轴角的集合为： ；终边在x 轴非正半轴角的集合为： ；故终边在x 轴上角的集合为： ；终边在y 轴非负半轴角的集合为： ；终边在y 轴非正半轴角的集合为： ；故终边在y 轴上角的集合为： ；终边在坐标轴上的角的集合为： .2. 弧度制：我们规定，长度等于半径的弧所对的圆心角叫做1弧度的角；用弧度来度量角的单位制叫做弧度制. 在弧度制下，1弧度记做1rad .(1) 角度与弧度之间的转换：① 将角度化为弧度： π2360=︒ π=︒180 rad 01745.01801≈=︒πrad n n 180π=︒② 将弧度化为角度：︒=3602π ︒=180π 815730.57)180(1'︒=︒≈︒=πrad ︒=) 180(πn n (2) 把上述象限角和轴线角用弧度表示.(3) 上述象限角和轴线角用弧度表示：; α⋅=r l 弧长公式：. 21lR S =扇形面积公式： 3. 任意角的三角函数：. 0 ),( (1)22>+=y x r y x P 是它与原点的距离，的坐标是其终边上任意一点是一个任意大小的角，设α ①;sin sin ry r y =ααα，即的正弦，记作叫做比值 ②;cos cos rx r x =ααα，即的余弦，记作叫做比值 ③.tan tan x y x y =ααα，即的正切，记作叫做比值(2) 判断各三角函数在各象限的符号：(3) 三角函数线：4. 同角三角函数基本关系式：(1) 平方关系： 1cos sin 22=+αα(2) 商数关系：αααcos sin tan =5. 诱导公式诱导公式(一) )Z (tan )2tan()Z (cos )2cos()Z (sin )2sin(∈=+∈=+∈=+k k k k k k ααπααπααπ诱导公式(二)tan )tan(cos )cos(sin )sin(ααπααπααπ=+-=+-=+诱导公式(三)tan )tan(cos )cos(sin )sin(αααααα-=-=--=-诱导公式(四)sin(π－α)=sin αcos(π －α)=－cos αtan (π－α)=－tan α诱导公式(五)ααπααπααπtan )2tan(cos )2cos(sin )2sin(-=-=--=-对于五组诱导公式的理解 ：可以是任意角；公式中的α .1.360,180, 180 , , )Z ( 360 .2符号看成锐角时原函数值的前面加上一个把它的同名三角函数值，于等的三角函数值，括为：这五组诱导公式可以概αααααα-︒-︒+︒-∈+︒⋅k k 函数名不变，符号看象限3.利用诱导公式将任意角三角函数转化为锐角三角函数的基本步骤：三、基础训练： ) ( sin ],2,[,23)(cos .1的值为则且已知αππααπ∈=+ 23 D. 21 C. 21- B. 21 A.±±23 D. 23 C. 21- B. 21 A.) ( )647(-cos .2-的值为π . __________)3cos(,tan )3tan(,101-)sin(3 .3=--=-=+παααπαπ则且若. _______)tan()cos(-)sin( .4=--⋅+απααπ化简： ) (cot tan ,32cos sin .5的值是则已知θθθθ+=+ 518- D. 45 C. 49 B. 185 A. . _____cos sin ,83cos sin .6=+=⋅ααααα是第三象限角，则且已知 四、典型例题：.),360,360(),2,2()2( _____630(1) 1.中绝对值最小的角，并求出的集合试写出角并且的终边经过点若角象限角；是第角，则后成为角边在按顺时针方向旋转是第二象限角，当其终若例A A P αααααθ︒︒-∈-︒ . ,30 125 (2) ___,43tan ___,34cos ___,3sin 2.(1)2求扇形的弧长和半径长弧度，面积为已知扇形的圆心角为计算：例cm πππππ===例3. 化简：设Z,∈k .])1cos[(])1sin[()cos()sin(απαπαπαπ-++++-k k k k 五、课堂小结1. 任意角的三角函数；2. 同角三角函数的关系；3. 诱导公式.六、课后作业1. 阅读教材P.67-P.68；2. 《习案》作业十六中1至6题.高中任一科任一课的教案、课件、试题、每年的高考试题及答案均可在免费免注册的教学资源网“备课吧”域名（谐音：123皮皮的呐）内搜到。

第一章 三角函数1.1任意角和弧度制1.1.1任意角一、 教学目标：1、知识与技能（1）推广角的概念、引入大于360︒角和负角；（2）理解并掌握正角、负角、零角的定义；（3）理解任意角以及象限角的概念；(4)掌握所有与α角终边相同的角（包括α角）的表示方法；（5）树立运动变化观点，深刻理解推广后的角的概念；（6）揭示知识背景，引发学生学习兴趣.（7）创设问题情景，激发学生分析、探求的学习态度，强化学生的参与意识.2、过程与方法通过创设情境：“转体720︒，逆（顺）时针旋转”，角有大于360︒角、零角和旋转方向不同所形成的角等，引入正角、负角和零角的概念；角的概念得到推广以后，将角放入平面直角坐标系，引入象限角、非象限角的概念及象限角的判定方法；列出几个终边相同的角，画出终边所在的位置，找出它们的关系，探索具有相同终边的角的表示；讲解例题，总结方法，巩固练习.3、情态与价值通过本节的学习，使同学们对角的概念有了一个新的认识，即有正角、负角和零角之分.角的概念推广以后，知道角之间的关系.理解掌握终边相同角的表示方法，学会运用运动变化的观点认识事物.二、教学重、难点重点: 理解正角、负角和零角的定义，掌握终边相同角的表示法.难点: 终边相同的角的表示.三、学法与教学用具之前的学习使我们知道最大的角是周角,最小的角是零角.通过回忆和观察日常生活中实际例子,把对角的理解进行了推广.把角放入坐标系环境中以后,了解象限角的概念.通过角终边的旋转掌握终边相同角的表示方法.我们在学习这部分内容时,首先要弄清楚角的表示符号,以及正负角的表示.另外还有相同终边角的集合的表示等.教学用具:电脑、投影机、三角板四、教学设想【创设情境】思考:你的手表慢了5分钟，你是怎样将它校准的？假如你的手表快了1.25小时，你应当如何将它校准？当时间校准以后，分针转了多少度？[取出一个钟表,实际操作]我们发现，校正过程中分针需要正向或反向旋转，有时转不到一周，有时转一周以上,这就是说角已不仅仅局限于0360︒︒~之间，这正是我们这节课要研究的主要内容——任意角.【探究新知】1．初中时，我们已学习了0360︒︒~角的概念，它是如何定义的呢？[展示投影]角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.如图1.1-1，一条射线由原来的位置OA ，绕着它的端点O 按逆时针方向旋转到终止位置OB ，就形成角α.旋转开始时的射线OA 叫做角的始边，OB 叫终边，射线的端点O 叫做叫α的顶点.2.如上述情境中所说的校准时钟问题以及在体操比赛中我们经常听到这样的术语：“转体720︒” （即转体2周），“转体1080︒”（即转体3周）等,都是遇到大于360︒的角以及按不同方向旋转而成的角.同学们思考一下:能否再举出几个现实生活中“大于360︒的角或按不同方向旋转而成的角”的例子,这些说明了什么问题?又该如何区分和表示这些角呢?[展示课件]如自行车车轮、螺丝扳手等按不同方向旋转时成不同的角, 这些都说明了我们研究推广角概念的必要性. 为了区别起见，我们规定:按逆时针方向旋转所形成的角叫正角(positive angle),按顺时针方向旋转所形成的角叫负角(negative angle).如果一条射线没有做任何旋转,我们称它形成了一个零角(zero angle).[展示课件]如教材图1.1.3(1)中的角是一个正角,它等于750︒；图1.1.3(2)中，正角210α︒=，负角150,660βγ︒︒=-=-；这样，我们就把角的概念推广到了任意角（any angle ）,包括正角、负角和零角. 为了简单起见，在不引起混淆的前提下，“角α”或“α∠”可简记为α.3.在今后的学习中，我们常在直角坐标系内讨论角，为此我们必须了解象限角这个概念. 角的顶点与原点重合，角的始边与x 轴的非负半轴重合。

人教A版数学必修4 第一章三角函数教学设计一、教材分析1、本单元教学内容的范围1.1 任意角的概念与弧度制1.1.1 角的概念的推广1.1.2 弧度制和弧度制与角度制的换算1.2 任意角的三角函数1.2.1 三角函数的定义1.2.2 单位圆与三角函数线1.2.3 同角三角函数的基本关系式1.2.4 诱导公式1.3 三角函数的图象与性质1.3.1 正弦函数的图象与性质1.3.2 余弦函数、正切函数的图象与性质1.3.3 已知三角函数值求角本章知识结构如下：2、本单元教学内容在模块内容体系中的地位和作用（1）三角函数是一类十分重要的初等函数，它与本模块第三章“三角恒等变换”构成了高中“三角”知识的主体，是中学数学的重要内容之一，也是学习后继内容和高等数学的基础。

（2）三角函数是数学中重要的数学模型之一，是研究度量几何的基础，又是研究自然界周期变化规律最强有力的数学工具。

（3）三角函数作为描述周期现象的重要数学模型，与其它学科如天文学、物理学等联系非常紧密。

因此三角函数的学习可以培养学生的数学应用能力。

（4）三角函数的基础知识，主要是平面几何中的相似形和圆。

研究三角函数的方法，主要是在必修1中建立的研究初等函数的方法。

因此，通过对三角函数的学习，可以初步地把“数”与“形”联系起来。

（5）通过对三角函数的学习，不仅能使学生获得新的知识和技能，而且可以培养学生的辨证唯物主义观点，提高分析问题和解决问题的能力。

3、本单元教学内容总体教学目标 （1）任意角的概念、弧度制了解任意角的概念．了解弧度制的概念，能进行弧度与角度的互化． （2）任意角的三角函数理解任意角的正弦、余弦、正切的定义；了解任意角的余切、正割、余割的定义；并会利用单位圆中的有向线段表示正弦、余弦和正切，并理解其原理。

理解同角三角函数的基本关系式： 22sin cos 1x x +=，sin tan cos xx x=；借助单位圆的直观性探索正弦、余弦、正切的诱导公式，能进行同角三角函数之间的变换，会求任意角的三角函数值，并记住某些特殊角的三角函数值。

人教版高中数学高一必修4第一章三角函数章末复习第1课时教案◆一、核心素养1.会用弧度制来表示角度，以及弧长公式和面积公式，借助单位圆理解任意角的三角函数（正弦、余弦、正切的定义；2.能根据任意角的三角函数的定义求出具体的角的各三角函数值；能根据定义探究出三角函数值在各个象限的符号。

3.掌握诱导公式并运用之进行三角函数式的求值、化简以及简单三角恒等式的证明．4.在定义的学习过程中渗透数形结合的思想。

◆二、教学重点、难点重点：能正确地进行弧度和角度的换算；会判断三角函数值的符号；能熟练地运用终边相同角的集合及诱导公式研究相关问题；能利用公式化简，证明三角函数式、三角恒等式。

难点：熟记特殊角的三角函数值，同角三角函数关系，善于运用特殊值解决问题。

◆三、教学过程设计回顾本章的整体内容，构建知识网络，启发、引导学生建立各节内容的知识结构图知识梳理：1、角的概念推广，零角，正角，负角推广到实数集R2、角度值与弧度制的互化特殊角的转化结果0 3、任意角的三角函数定义(1)与a 终边相同的角的集合A={x|x=a+k.360}(2)第一象限角的表示方法从而推到所以象限角的表示以及坐标角的表示方法︒306π︒454π3π︒602π︒12032π︒13543π︒15065π︒270π23π︒180 ︒0︒360π2︒90y x x r y r x y rx r y ======ααααααcot ,sec ,csc tan ,cos ,sin符号口诀：一全正，二正弦，三正切，四余弦4、同角三角函数关系式aa a cos sin tan = 1cos sin 22=+a a5、三角函数线6、诱导公式 奇变偶不变，符号看象限例题练习：本题目的是为了练习弧长公式以及三角函数定义的应用例2、已知扇形周长为20cm ，当半径和圆心角为多少时，才能使扇形面积最大，最大面积为多少？本题是为了明确弧度制实际上是实数集范围内的，又结合了二次函数求值域的方法。