电工技术：复数的表示形式及复数的四则运算

复数的基本运算与性质复数是数学中一种重要的数，包括实部和虚部。

在复数运算中，我们将探讨复数的基本运算规则和性质。

一、复数的表示形式复数可以用标准形式或者三角形式来表示。

标准形式为a+bi，其中a为实部，b为虚部，i为虚数单位。

三角形式为r(cosθ+isinθ)，其中r 为模，θ为辐角。

二、复数的加法复数的加法与实数的加法类似。

将两个复数的实部相加得到新复数的实部，虚部相加得到新复数的虚部。

例如，将复数z1=a1+b1i和复数z2=a2+b2i相加得到新复数z=a+b。

三、复数的减法复数的减法与实数的减法类似。

将被减数减去减数的实部得到新复数的实部，虚部相减得到新复数的虚部。

例如，将复数z1=a1+b1i减去复数z2=a2+b2i得到新复数z=a+b。

四、复数的乘法复数的乘法是根据乘法分配律进行计算的。

将实部相乘减去虚部相乘得到新复数的实部，实部相乘再相加得到新复数的虚部。

例如，将复数z1=a1+b1i和复数z2=a2+b2i相乘得到新复数z=a+b。

五、复数的除法复数的除法是根据乘法的逆运算进行计算的。

将复数的实部相乘再相加除以模的平方，得到新复数的实部；将虚部相乘再相减除以模的平方，得到新复数的虚部。

例如，将复数z1=a1+b1i除以复数z2=a2+b2i得到新复数z=a+b。

六、复数的共轭复数的共轭是将复数的虚部取负得到的新复数。

即将复数z=a+bi的共轭为z*=a-bi。

七、复数的乘方复数的乘方是将复数自乘n次得到的结果。

例如，将复数z=a+bi自乘n次得到z^n。

八、复数的性质1. 加法的交换律：z1+z2=z2+z12. 加法的结合律：(z1+z2)+z3=z1+(z2+z3)3. 乘法的交换律：z1*z2=z2*z14. 乘法的结合律：(z1*z2)*z3=z1*(z2*z3)5. 分配律：z1*(z2+z3)=z1*z2+z1*z3以上是复数的基本运算与性质的介绍。

复数运算在数学中有着广泛的应用，特别是在物理学和工程学领域中。

电路基础原理交流电路中的复数形式与复数运算电路基础原理：交流电路中的复数形式与复数运算电路是电子科学与技术中的重要分支，交流电路是其中一类最常见的电路。

交流电路是指电压或电流的方向和大小周期性变化的电路。

在交流电路中，复数形式与复数运算是理解和分析电路行为的重要工具。

交流电路中的电压和电流可以用复数表示。

复数是由实部和虚部构成的数学对象。

在电学中，实部表示电压或电流的振幅，虚部表示相位角。

通过将交流电压或电流看作复数，我们可以用更简洁的方式表示电路中的信号。

复数形式也便于进行电路参数之间的计算和分析。

复数形式的交流电压和电流是通过欧姆定律和基尔霍夫定律推导得到的。

在交流电路中，电压和电流的频率通常是固定的，因此可以用复数形式表示交流电压和电流。

我们通常将复数形式的交流电压表示为V=|V|∠θ，其中|V|表示电压的幅值，θ表示相位角。

同样，复数形式的交流电流表示为I=|I|∠φ，其中|I|表示电流的幅值，φ表示相位角。

相位角表示了电压和电流之间的相对关系，它们的变化可以描述电路中的频率和相位差。

复数运算在交流电路分析中扮演着重要角色。

复数的加法和减法可以用来计算电压和电流的叠加效果。

例如，当两个电源连接到一个电路上时，通过复数运算可以计算出总电压和总电流。

复数的乘法和除法可以用来计算电路中的电压和电流的变换。

例如，当电压经过电感时，可以用乘法计算出电感的负载。

在交流电路中，阻抗是一个重要的概念。

阻抗是复数形式中电压和电流之间的比值。

复数形式的电压和电流可以写为V=IZ，其中Z表示复数形式的阻抗。

阻抗是在交流电路中表示电阻、电感和电容的有效值。

利用复数运算，我们可以方便地计算电路中的阻抗，从而分析交流电路的性质。

除了用于分析交流电路之外，复数形式与复数运算还在实际电路设计中起着重要作用。

在实际电路设计中，我们通常使用电阻、电感和电容来构建各种功能电路。

通过使用复数形式和复数运算，我们可以更好地理解和设计这些电路。

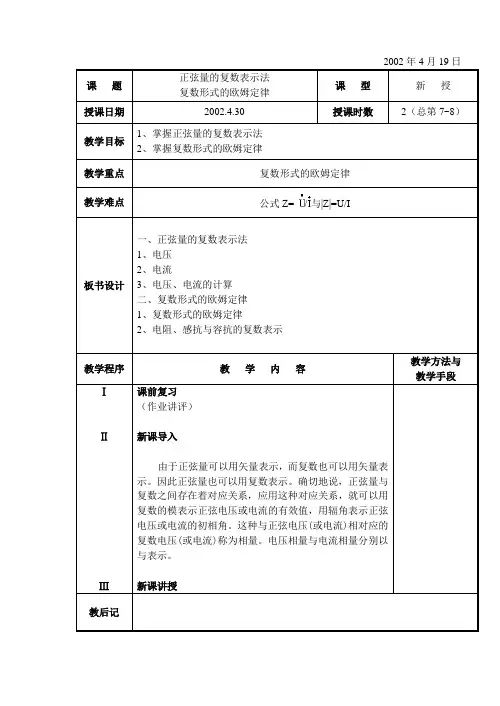
2002年4月19日课题正弦量的复数表示法复数形式的欧姆定律课型新授授课日期2002.4.30 授课时数2（总第7~8）教学目标1、掌握正弦量的复数表示法2、掌握复数形式的欧姆定律教学重点复数形式的欧姆定律教学难点公式Z= /与|Z|=U/I板书设计一、正弦量的复数表示法1、电压2、电流3、电压、电流的计算二、复数形式的欧姆定律1、复数形式的欧姆定律2、电阻、感抗与容抗的复数表示教学程序教学内容教学方法与教学手段ⅠⅡⅢ课前复习（作业讲评）新课导入由于正弦量可以用矢量表示，而复数也可以用矢量表示。

因此正弦量也可以用复数表示。

确切地说，正弦量与复数之间存在着对应关系，应用这种对应关系，就可以用复数的模表示正弦电压或电流的有效值，用辐角表示正弦电压或电流的初相角。

这种与正弦电压(或电流)相对应的复数电压(或电流)称为相量。

电压相量与电流相量分别以与表示。

新课讲授教后记教学程序教学内容教学方法与教学手段一、正弦量的复数表示法正弦交流电的解析式与复数之间的对应关系可表示为1、电压u=Usin（ωt+φu0）=U∠φu02、电流i=Isin（ωt+φi0）=I∠φi0例如：u=220sin（ωt+30°）V，i=5sin（ωt－60°）A 将它们表示成有效值的相量式为=220∠30°V，=5∠－60°A这也就是正弦交流电有效值的复数表示式。

上述电压相量与电流相量的相量图，如图所示。

3、电压、电流的计算用相量表示正弦交流电后，正弦交流电路的分析与计算就可以用复数来进行。

例题1、已知两个正弦交流电流为i1=6sin（ωt＋120°）A，i2=8sin（ωt＋30°）A，用相量来表示它们，并求它们的与。

举例讲解板书作图例题1教后记教学程序教学内容教学方法与教学手段解：i1与i2分别用相量表示为1=6∠120°A2=8∠30°A将复数的极坐标表示式变换为代数表示式，分别为1=6∠120°A=（－3＋j5.2）A2=8∠30°A=（6.9＋j4）A所以=1＋2=（－3＋j5.2＋6.9＋j4）A=（3.9＋j9.2）A=10∠67°A最后，将电流相量写成对应的解析式i=10sin（ωt＋67°）A。

高一数学必修1复数的四则运算知识点讲解数学课程中学习复数代数形式的四则运算时,重点理解四则运算法则、运算律以及复数加减法的几何意义。

下面是店铺给大家带来的高一数学必修1复数的四则运算知识点讲解，希望对你有帮助。

高一数学复数的四则运算知识点(一)复数的概念：形如a+bi(a，b∈R)的数叫复数，其中i叫做虚数单位。

全体复数所成的集合叫做复数集，用字母C表示。

复数的表示：复数通常用字母z表示，即z=a+bi(a，b∈R)，这一表示形式叫做复数的代数形式，其中a叫复数的实部，b叫复数的虚部。

复数的几何意义：(1)复平面、实轴、虚轴：点Z的横坐标是a，纵坐标是b，复数z=a+bi(a、b∈R)可用点Z(a，b)表示，这个建立了直角坐标系来表示复数的平面叫做复平面，x轴叫做实轴，y轴叫做虚轴。

显然，实轴上的点都表示实数，除原点外，虚轴上的点都表示纯虚数(2)复数的几何意义：复数集C和复平面内所有的点所成的集合是一一对应关系，即这是因为，每一个复数有复平面内惟一的一个点和它对应;反过来，复平面内的每一个点，有惟一的一个复数和它对应。

这就是复数的一种几何意义，也就是复数的另一种表示方法，即几何表示方法。

复数的模：复数z=a+bi(a、b∈R)在复平面上对应的点Z(a，b)到原点的距离叫复数的模，记为|Z|，即|Z|=虚数单位i：(1)它的平方等于-1，即i2=-1;(2)实数可以与它进行四则运算，进行四则运算时，原有加、乘运算律仍然成立(3)i与-1的关系：i就是-1的一个平方根，即方程x2=-1的一个根，方程x2=-1的另一个根是-i。

(4)i的周期性：i4n+1=i，i4n+2=-1，i4n+3=-i，i4n=1。

复数模的性质：复数与实数、虚数、纯虚数及0的关系：对于复数a+bi(a、b∈R)，当且仅当b=0时，复数a+bi(a、b∈R)是实数a;当b≠0时，复数z=a+bi叫做虚数;当a=0且b≠0时，z=bi叫做纯虚数;当且仅当a=b=0时，z就是实数0。

交流电路中的复数表示法在电子技术中，交流电路是一个重要的概念。

在交流电路中，电流和电压随时间而变化，因此需要一种方法来表示这种变化。

复数表示法是一种常用的方法，它能有效地描述交流电路中电压和电流的变化。

复数表示法是基于复数的概念，其中虚数单位'i'被定义为√(-1)。

在交流电路中，电压和电流可以用复数来表示，其中实数部分表示电压或电流的幅值，虚数部分表示相位角或相位差。

以交流电压为例，它可以用以下形式表示：V = Vm * cos(ωt + φ)，其中V是电压的复数表示形式，Vm是电压的幅值，ω是角频率，t是时间，φ是相位角。

复数形式的电流表示也类似。

复数表示法的优点之一是它能方便地进行计算。

在复平面上，电压和电流可以表示为一个向量，在计算时可以使用向量的运算规则。

例如，两个电压的复数表示形式相乘时，只需要将它们对应的幅值相乘，相位角相加。

此外，复数表示法还可以很好地描述电压和电流之间的关系。

由于虚数单位'i'的定义，相位差可以用虚数表示。

例如，当两个电压的复数表示形式相减时，得到的结果即为它们之间的相位差。

复数表示法在分析和设计交流电路时非常有用。

通过将电压和电流用复数表示，我们可以方便地进行计算和推导。

例如，通过复数表示法可以方便地推导出频率选择电路的传递函数，进而分析电路的频率响应。

此外，复数表示法还使得交流电路的分析更加简洁。

以欧姆定律为例，我们知道在直流电路中，电压等于电流乘以电阻。

然而，在交流电路中，电压和电流存在相位差的情况，导致简单的乘法不再成立。

通过使用复数表示法，我们可以方便地将电阻、电感和电容的作用整合在一起，从而得到更简洁的表达式。

综上所述，复数表示法在交流电路中扮演着重要角色。

它能够方便地进行计算和推导，同时提供了更简洁的电路分析方法。

掌握复数表示法有助于我们更好地理解和设计交流电路。

在电子技术的学习和实践中，复数表示法是一个不可或缺的工具。

高考数学中的复数基本概念及相关性质复数是高中数学中的一个基础概念，也是考研、考博、研究生数学课程中的重要内容。

复数可以表示成实部加虚部的形式，其中虚部用单位虚数 $i$ 表示。

本文将主要介绍高考数学中的复数基本概念及相关性质，包括常见的复数表示法、复数的四则运算、复数的共轭、模、幅角，并结合一些例题进行详解。

一、复数的表示法1. 普通表示法形如 $a + bi$ 的形式，其中 $a$ 为实部，$b$ 为虚部，$i$ 为虚数单位。

2. 模角表示法形如 $r(\cos\theta + i\sin\theta)$ 的形式，其中 $r$ 为复数的模，$\theta$ 为复数的幅角。

二、复数的四则运算复数相加减可以看做实部和虚部分别相加减，即 $(a + bi) \pm (c + di) = (a \pm c) + (b \pm d)i$。

复数相乘时，利用分配律得到 $(a + bi)(c + di) = ac + adi + bic + bdi^2$，因为 $i^2 = -1$，所以 $bdi^2 = -bd$，将其代入可得 $(ac - bd) + (ad + bc)i$。

对于复数相除这一运算，在分子分母同时乘上分母的共轭，然后利用分配律将虚部表示出来进行化简，可以得到 $\dfrac{a + bi}{c + di} = \dfrac{(a + bi)(c - di)}{c^2 + d^2} = \dfrac{ac + bd}{c^2 + d^2} + \dfrac{bc - ad}{c^2 + d^2}i$。

三、复数的共轭、模、幅角复数 $a + bi$ 的共轭为 $a - bi$，可以用于求模和幅角。

设 $z = a + bi$，则 $|z| = \sqrt{a^2 + b^2}$，$\text{Arg}z$ 为 $z$ 的幅角，满足 $z = |z|(\cos\text{Arg}z + i\sin\text{Arg}z)$。

复数基础知识及其运算规律一、复数的概念1.复数的定义：复数是由实数和虚数构成的数，一般形式为a+bi，其中a和b分别为实数，i为虚数单位，满足i^2=-1。

2.复数的分类：a)纯虚数：实部为0的复数，如i、-i等；b)实数：虚部为0的复数，如2、-3等；c)混合数：实部和虚部都不为0的复数，如1+2i、-3-4i等。

二、复数的表示方法1.代数表示法：用a+bi的形式表示复数；2.极坐标表示法：用r(cosθ+isinθ)的形式表示复数，其中r为模长，θ为辐角。

三、复数的运算规律1.加减法：a)(a+bi) + (c+di) = (a+c) + (b+d)i；b)(a+bi) - (c+di) = (a-c) + (b-d)i。

c)(a+bi)(c+di) = (ac-bd) + (ad+bc)i；d)特殊情形：两个纯虚数相乘，结果为实数；e)单位根的乘法：i^k，其中k为整数。

f)(a+bi)/(c+di) = [(ac+bd)/(c2+d2)] + [(bc-ad)/(c2+d2)]i。

g)(a+bi)^2 = (a2-b2) + 2abi；h)(a+bi)3、(a+bi)4等，可以利用乘方公式进行展开。

2.共轭复数：a)若复数为a+bi，则它的共轭复数为a-bi；b)共轭复数具有以下性质：两数相加为实数，两数相乘为实数。

四、复数的性质1.模长：表示复数在复平面上的长度，公式为|a+bi| = √(a2+b2)；2.辐角：表示复数在复平面上与实轴的夹角，公式为θ = arctan(b/a)，其中a≠0；3.复数的平方等于1的解：i、-1、1+i、1-i等；4.复数的平方等于-1的解：i、-i等；5.复数的平方等于k（k为非零实数）的解：±√k、±i√k等。

五、复数在实际应用中的例子1.信号处理：在通信系统中，信号往往可以表示为复数形式，如调制解调器中的正弦波信号；2.物理学：在电磁学、量子力学等领域，复数用于描述物理量，如电流、电压、波函数等；3.工程学：在电子工程、控制理论等领域，复数用于分析电路、系统稳定性等。

高一数学必修二复数知识点笔记一、复数的概念和表示方法复数是由一个实数和一个虚数组成，通常写作a + bi的形式，其中a为实部，b为虚部，i为虚数单位。

表示复数的常用形式包括标准形式、三角形式和指数形式。

二、复数的四则运算1. 加法和减法复数加法：(a + bi) + (c + di) = (a + c) + (b + d)i复数减法：(a + bi) - (c + di) = (a - c) + (b - d)i2. 乘法和除法复数乘法：(a + bi) × (c + di) = (ac - bd) + (ad + bc)i复数除法：(a + bi) ÷ (c + di) = [(ac + bd) ÷ (c² + d²)] + [(bc - ad) ÷ (c² + d²)]i3. 幂运算复数的n次幂：(a + bi)ⁿ = (rⁿcos(nθ)) + (rⁿsin(nθ))i其中，r为复数的模，θ为复数的幅角。

三、复数共轭和模1. 复数的共轭设有复数z = a + bi，则z的共轭复数记作z* = a - bi。

具体来说，如果一个复数的虚部为正数b，则它的共轭复数则为虚部为负数-b。

2. 复数的模设有复数z = a + bi，则z的模记作|z| = √(a² + b²)。

复数模的计算公式即为将复数的实部和虚部的平方和开方。

四、复数的三角形式和指数形式1. 复数的三角形式设有复数z = a + bi，其模为r，幅角为θ，则z可表示为z= r(cosθ + isinθ)。

具体来说，复数的三角形式包括两部分，一部分是mod_r= r，另一部分是arg_z = θ。

2. 复数的指数形式复数的指数形式可以通过欧拉公式得到，即z = r^(iθ) = e^(iθ)。

其中，e为自然对数的底，i为虚数单位。

五、复数在解析几何中的应用1. 复数与向量复数可以用来表示平面上的向量，实部和虚部分别表示向量的x和y坐标。