管理运筹学讲义 第6章动态规划
- 格式:ppt
- 大小:1.09 MB
- 文档页数:84

第6章 动态规划动态规划(Dynamic Programming )是解决多阶段决策过程最优化的一种有用的数学方法。
它是由美国学者Richard .Bellman 在1951年提出的,1957年他的专著《动态规划》一书问世,标志着运筹学的一个重要分支-动态规划的诞生.动态规划也是一种将多变量问题转化为单变量问题的一种方法。
在动态规划中,把困难的多阶段决策问题变换成一系列相互联系的比较容易的单阶段问题一个个地求解。
动态规划是考察解决问题的一种途径 ,而不是一种特殊的算法,不像线性规划那样有统一的数学模型和算法(如单纯形法).事实上,在运用其解决问题的过程中还需要运用其它的优化算法。
因此,动态规划不像其它方法局限于解决某一类问题,它可以解决各类多阶段决策问题。
动态规划在工程技术、经济管理等社会各个领域都有着广泛的应用,并且获得了显著的效果。
在经济管理方面,动态规划可以用来解决最优路径问题、资源分配问题、生产调度问题、库存管理问题、排序问题、设备更新问题以及生产过程最优控制问题等,是经济管理中一种重要的决策技术。
许多规划问题用动态规划的方法来处理,常比线性规划或非线性规划更有效。
特别是对于离散的问题,由于解析数学无法发挥作用,动态规划便成为了一种非常有用的工具。
动态规划可以按照决策过程的演变是否确定分为确定性动态规划和随机性动态规划;也可以按照决策变量的取值是否连续分为连续性动态规划和离散性动态规划。
本教材主要介绍动态规划的基本概念、理论和方法,并通过典型的案例说明这些理论和方法的应用。
6.1动态规划的基本理论6.1.1多阶段决策过程的数学描述有这样一类活动过程,其整个过程可分为若干相互联系的阶段,每一阶段都要作出相应的决策,以使整个过程达到最佳的活动效果。
任何一个阶段(stage ,即决策点)都是由输入(input )、决策(decision )、状态转移律(transformation function )和输出(output )构成的,如图6-1(a )所示.其中输入和输出也称为状态(state ),输入称为输入状态,输出称为输出状态。






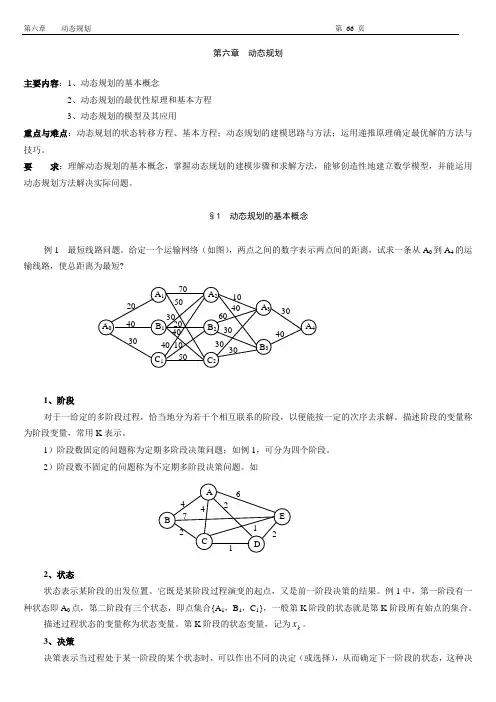
第六章 动态规划主要内容:1、动态规划的基本概念2、动态规划的最优性原理和基本方程3、动态规划的模型及其应用重点与难点:动态规划的状态转移方程、基本方程;动态规划的建模思路与方法;运用递推原理确定最优解的方法与技巧。
要 求:理解动态规划的基本概念,掌握动态规划的建模步骤和求解方法,能够创造性地建立数学模型,并能运用动态规划方法解决实际问题。
§1 动态规划的基本概念例1 最短线路问题。
给定一个运输网络(如图),两点之间的数字表示两点间的距离,试求一条从A 0到A 4的运输线路,使总距离为最短?1、阶段对于一给定的多阶段过程,恰当地分为若干个相互联系的阶段,以便能按一定的次序去求解。
描述阶段的变量称为阶段变量,常用K 表示。
1)阶段数固定的问题称为定期多阶段决策问题;如例1,可分为四个阶段。
2)阶段数不固定的问题称为不定期多阶段决策问题。
如2、状态状态表示某阶段的出发位置。
它既是某阶段过程演变的起点,又是前一阶段决策的结果。
例1中,第一阶段有一种状态即A 0点,第二阶段有三个状态,即点集合{A 1,B 1,C 1},一般第K 阶段的状态就是第K 阶段所有始点的集合。
描述过程状态的变量称为状态变量。
第K 阶段的状态变量,记为k x 。
3、决策决策表示当过程处于某一阶段的某个状态时,可以作出不同的决定(或选择),从而确定下一阶段的状态,这种决A 0A 1B 1C 1A 2B 2C 2B 3A 3A 420 40 3070 5030 2040 40 1050 10 4060 3030 3030 40B ACDE4 724 2621 1定称为决策。
描述决策的变量称为决策变量,常用)(k k x u 表示处于状态k x 时的决策变量,它是状态变量的函数。
如: 21A B → , 记为()212A B U =决策变量可取值的全体,称为允许决策集合。
常用()k k x D 表示状态k x 的允许决策集合。



第六章 单纯形法的灵敏度分析与对偶• §1 单纯形表的灵敏度分析 • §2 线性规划的对偶问题 • §3 对偶规划的基本性质 • §4 对偶单纯形法§1 单纯形表的灵敏度分析一、目标函数中变量C k系数灵敏度分析1. 在最终的单纯形表里,X k 是非基变量由于约束方程系数增广矩阵在迭代中只是其本身的行的初等变换与C k 没有任何关系,所以当C k 变成C k +ΔC k 时,在最终单纯形表中其系数的增广矩阵不变,又因为X k 是非基变量,所以基变量的目标函数的系数不变,即C B 不变,可知Z k 也不变,只是C k 变成了C k +ΔC k 。
这时δK = C k -Z k 就变成了C k +ΔC k - Z k =δK +ΔC k 。
要使原来的最优解仍为最优解,只要δK + ΔC k ≤0即可,也就是C k 的增量ΔC k ≤—δK 。
2. 在最终的单纯形表中, X k 是基变量当C k 变成C k + ΔC k 时,最终单纯形表中约束方程的增广矩阵不变,但是基变量的目标函数的系数C B 变了,则Z J (J=1,2,…,N)一般也变了,不妨设C B =(C B1, C B2…, C k ,…,C Bm ),当C B 变成=(C B1, C B2…,C k + ΔC k ,…,C Bm ),则:Z J =(C B1, C B2…, C k ,…,C Bm )(a’1j , a’2j ,…, a’Kj ,…, a’mj )Z’J =(C B1, C B2…, C k +ΔC k ,…,C Bm )(a’1j , a’2j ,…, a’Kj ,…, a’mj ) T = Z J + ΔC k a’Kj根据上式可知检验数δJ (J=1,2,…..,M)变成了δ’J ,有δ’ J =C J -Z’J =δJ +ΔC K a’Kj 。
要使最优解不变,只要当J ≠K 时,δ’J <=0⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>-≤≤⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<--≥-≤===⋅--+=-+==≤--≥<≥--≤>-≤≤+0a'a'δMin ΔC 0a'a'δMax ΔC a'δΔC a'0a'δΔC a'0a'0δ'1a'0δX ,a'ΔC Z ΔC C 'Z ΔC C δ'k j ;0a'δ,a'δΔC ,0a';0a'δ,a'δΔC ,0a'δa'ΔC 0,a'ΔC δkj kj jk kj kj j kkjjkkjkjj k kjkkkkkkK kk k k k k k k k k kjj kjj k kj kj j kj j k kj jkj k kj k j 的变化范围为,所以可知满足的,所有小于,满足的以外的所有大于于除了要使得最优解不变,对。