基于小波变换的瑞利波信号去噪分析
- 格式:pdf
- 大小:529.66 KB
- 文档页数:4

小波分析的语音信号噪声消除方法小波分析是一种有效的信号处理方法,可以用于噪声消除。
在语音信号处理中,噪声常常会影响语音信号的质量和可理解性,因此消除噪声对于语音信号的处理非常重要。
下面将介绍几种利用小波分析的语音信号噪声消除方法。
一、阈值方法阈值方法是一种简单而有效的噪声消除方法,它基于小波变换将语音信号分解为多个频带,然后通过设置阈值将各个频带的噪声成分消除。
1.1离散小波变换(DWT)首先,对语音信号进行离散小波变换(DWT),将信号分解为近似系数和细节系数。
近似系数包含信号的低频成分,而细节系数包含信号的高频成分和噪声。
1.2设置阈值对细节系数进行阈值处理,将细节系数中幅值低于设定阈值的部分置零。
这样可以将噪声成分消除,同时保留声音信号的特征。
1.3逆变换将处理后的系数进行逆变换,得到去噪后的语音信号。
1.4优化阈值选择为了提高去噪效果,可以通过优化阈值选择方法来确定最佳的阈值。
常见的选择方法有软阈值和硬阈值。
1.4.1软阈值软阈值将细节系数进行映射,对于小于阈值的细节系数,将其幅值缩小到零。
这样可以在抑制噪声的同时保留语音信号的细节。
1.4.2硬阈值硬阈值将细节系数进行二值化处理,对于小于阈值的细节系数,将其置零。
这样可以更彻底地消除噪声,但可能会损失一些语音信号的细节。
二、小波包变换小波包变换是对离散小波变换的改进和扩展,可以提供更好的频带分析。
在语音信号噪声消除中,小波包变换可以用于更精细的频带选择和噪声消除。
2.1小波包分解将语音信号进行小波包分解,得到多层的近似系数和细节系数。
2.2频带选择根据噪声和语音信号在不同频带上的能量分布特性,选择合适的频带对语音信号进行噪声消除。
2.3阈值处理对选定的频带进行阈值处理,将噪声成分消除。
2.4逆变换对处理后的系数进行逆变换,得到去噪后的语音信号。
三、小波域滤波小波域滤波是一种基于小波变换的滤波方法,通过选择合适的小波函数和滤波器来实现噪声消除。

摘要小波变换是一种新型的数学分析工具,是80年代后期迅速发展起来的新兴学科。
小波变换具有多分辨率的特点,在时域和频域都具有表征信号局部特征能力,适合分析非平稳信号,可以由粗及精地逐步观察信号。
小波分析的理论和方法在信号处理、图像处理、语音处理、模式识别、量子物理等领域得到越来越广泛的应用,它被认为是近年来在工具及方法上的重大突破。
信号的采集与传输过程中,不可避免会受到大量噪声信号的干扰,对信号进行去噪,提取出原始信号是一个重要的课题。
那么究竟应该如何从含噪声的信号中提取出原始的信号,这就成了最重要的问题。
经过长期的探索与努力、实验仿真,对比于加窗傅里叶对信号去噪,提取原始信号的方法,终于找到了一种全新的信号处理方法——小波分析。
它将信号中各种不同的频率成分分解到互不重叠的频带上,为信号滤波、信噪分离和特征提取提供了有效途径,特别在信号去噪方面显出了独特的优势。
本文从小波变换的定义和信号与噪声的不同特性出发,在对比分析了各种去噪方法的优缺点基础上,运用了对小波分解系数进行阈值化的方法来对一维信号去噪,该方法对去除一维平稳信号含有的白噪声有非常满意的效果,具有有效性和通用性,能提高信号的信噪比。
与此同时,本文还补充介绍了强制消噪处理、默认阈值处理、给定软阈值处理等对信号消噪的方法。
在对含噪信号运用阈值进行消噪的过程中,对比了用不同分解层数进行处理的去噪效果。
本文采用的是用传感器采集的微弱生物信号。
生物信号通常是噪声背景小的低频信号,而噪声信号通常集中在信号的高频部分。
因此,应用小波分解,把信号分解成不同频率的波形信号,并对高频波进行相关的处理,处理后的高频信号在和分离出的低频信号进行重构,竟而,就得到了含少量噪声的原始信号。
而且,随着分解层数的不同,小波去噪的效果也是不同的。
并对此进行了深入的分析。
关键词:小波变换;声信号;默认阈值处理;降噪小波重构The signal denoising based on wavelet transformQING Xue-zhenAbstractWavelet transform is a new-style mathematic analysis tool. Itis a new subjectwhich was rapidly developed inlate 1980s. The wavelet transform has the characteristicof multi-analysis and the ability to analyse partial characteristic both in the time domainand the frequency range, so it is suitable to analyze non-steady state signal and observesignal gradually from coarse to fine. The method has been used in many domains suchas signal processing, image processing, pronunciation distinction, pattern recognition,quantum physics and so on. It is considered as a great breakthrough of tools andmethods recently.It is inevitable to be interfered by a large amount of noise signal in the process of signal gathering and transmission. It’s a main topic to deniose and extract originalsignal.How should contain the noise signal from the original signal, which became a most important problem. After a long period of exploration and efforts, experimental simulation, compared to add window Fourier to signal denoising, extraction method of original signal, finally found a new signal processing method, wavelet analysis. It will signal in different frequency components of the decomposition into non-overlapping band, signal-to-noise ratio (SNR) for signal filtering, feature extraction separation and provides effective ways, especially in the aspect of signal denoising show a unique advantage.This article from the definition of wavelet transform and the different characteristics of signal and noise, the comparison and analysis the advantages and disadvantages of various denoising method, based on the use of the wavelet decomposition coefficient method for one-dimensional signal threshold denoising, the method for denoising the white noise of one dimensional steady signal contains a very satisfactory results, with the effectiveness and generality, can improve the SNR of signal. At the same time, this paper adds the compulsory treatment, the default threshold denoising, given the soft threshold processing method for signal de-noising. On noise signal using the threshold de-noising, compared with different decomposition layers for processing the denoising effect.This article USES the sensor with a weak biological signal acquisition. Biological signal is usually low frequency signal of background noise, the noise signal is usually focused on the highfrequency part of signal. Wavelet decomposition, therefore, the signal is decomposed into different frequency waveform signal, and the high frequency wave are related to processing, processing of high frequency signal in low frequency signal and isolated refactoring, unexpectedly and, get the original signal containing a small amount of noise. And as the number of decomposition layers, wavelet denoising effects are also different. And carried on the thorough analysis.Key words: wavelet transform; pronunciation signal;The default threshold processing;wavelet reconstruction目录1 绪论 (1)1.1 研究背景 (1)1.2 小波分析的研究现状 (3)1.3 本文研究的内容 (3)2 小波分析概述 (5)2.1 小波分析的定义 (5)2.2 小波变化的时、频局部性 (6)2.3 小波去噪常用的算法 (7)3 实验仿真 (8)3.1 一维小波去噪原理 (8)3.1.1 小波降噪的两个准则 (8)3.1.2 小波分析用于降噪的步骤 (8)3.1.3小波去噪的基本模型 (8)3.2基于阈值对生物信号消噪的运行结果 (10)4 结论 (13)4.1 本文工作总结 (13)4.2 小波分析的发展前景 (13)参考文献 (15)附录 (17)致谢 (18)1 绪论1.1 研究背景自从1822年傅里叶(Fourier)提出非周期信号分解概念以来,傅里叶变换一直是信号处理领域中应用最广泛的分析手段和方法,傅里叶变换是一种纯频域的分析方法,在时域无任何定位性,即不能提供任何局部时间段上的频率信息。

基于小波分析的信号去噪小波分析是一种用于信号处理的数学工具,可以用于信号的去噪。
它能够有效地分解信号并在不同频率和时间尺度上进行分析。
在信号处理中,噪声是不可避免的,因此去除噪声是非常重要的。
在这篇文章中,我们将介绍使用小波分析进行信号去噪的方法。
首先,让我们了解一下信号的特性。
信号可以分为两种类型:确定性信号和随机信号。
确定性信号是指在给定时间内具有确定的数学函数形式的信号,而随机信号是在给定时间内以随机方式变化的信号。
噪声通常是由随机信号引起的,而小波分析可以有效地处理这种随机信号的噪声。
小波分析使用小波函数对信号进行分解,这些小波函数具有平滑和局部化特性。
通过分解信号,我们可以将信号分解为具有不同频率和时间尺度的子信号。
然后,我们可以通过滤波来去除噪声,并重新构造干净的信号。
小波分析的主要步骤如下:1. 选择适当的小波函数:小波函数的选择取决于信号的特性。
常用的小波函数有Haar小波、Daubechies小波和Symlet小波等。
根据信号的特点选择合适的小波函数是非常重要的。
2.进行小波分解:将信号分解成不同尺度的子信号。
这可以通过对信号进行多级小波分解来实现。
在每个尺度上,信号被分解为近似系数和细节系数。
3.对细节系数进行滤波:由于噪声主要包含在细节系数中,所以我们需要对细节系数进行滤波来去除噪声。
可以使用阈值滤波等方法来实现。
4.合成信号:将滤波后的细节系数和近似系数合成为一个信号。
合成信号将不包含噪声。
小波分析的一个重要优点是它具有局部化特性。
这意味着小波分析可以在频域和时间域上同时提供信息。
这使得它在信号去噪中非常有用,因为它能够有效地捕捉到噪声的频率和时间特征。
除了去噪之外,小波分析还可以应用于信号压缩、模式识别和特征提取等领域。
它在图像处理中也得到了广泛应用。
综上所述,小波分析是一种有效的信号去噪方法。
通过对信号进行小波分解和滤波处理,可以成功去除噪声,得到干净的信号。
小波分析的局部化特性使其在信号处理中得到广泛应用,并在实际应用中取得了很好的效果。

基于小波变换和维纳滤波的半导体器件1 /f 噪声滤波1. 引言1 / f 信号最早是在1925 年对真空管的研究中作为一种超低频噪音被发现和研究的,它具有非平稳性、自相似性、持久相关性和1 / f 类型的功率谱密度等特性,广泛地存在于各类半导体器件中[1,2].对于1 / f 噪声具体的产生机理以及影响1 / f 噪声的物理机理,前人针对晶体管、结型场效应管和金属氧化物半导体场效管等器件进行了深入而广泛的研究[3,4],而如何从1 / f 噪声中提取有用信号是在半导体器件的使用过程中经常遇到的问题,比方对用于信号调理的模拟电路而言,当有用信号的频率较低时,用于放大、滤波的半导体器件产生的1 / f 噪声是主要噪声,如果不能滤除,1 / f 噪声将直接导致输出信号的低频漂移.考虑到1 / f 信号的小波变换域特性,本文首先估计了1 / f 噪声的参数,提出对叠加了1 / f 噪声的有用信号进行提升小波变换,而后利用有限冲击响应( FIR) 型维纳滤波器处理每一个尺度下的小波变换系数,最后进行逆提升小波变换重建有用信号的方法.2. 1 /f 噪声及其小波变换域特性1 / f 噪声通常是以它的功率谱定义,如果半导体器件的某种噪声电压信号f( x) 的能量主要集中在低频阶段,其功率谱Sf( ω) 满足Sf( ω) = AIσωγ, ( 1)式中σ和γ是常数,A 是由器件结构决定的参数,I表示通过器件的电流,则称f( x) 为1 / f 噪声[5].值得注意的是,( 1) 式中当γ> 1 时,Sf( ω) 的积分为无穷大,通常假设存在一个很低的频率,低于该频率功率谱的形状发生变化,Sf( ω) 变得可积,对实际器件的测试说明,这个很低的频率确实存在[5]. Tewfik等[6]利用分数布朗运动模型研究了1 / f 噪声在小波变换域的信号特征,他们已经证明,如果正交小波的消失矩R 满足R >γ /2,利用该小波对1 / f 噪声进行离散小波变换,得到的细节系数序列的持久相关性和自相似性被大幅度地削弱,可以认为是相互独立的随机变量,也就是小波变换能够将1 / f 噪声“白化”.这就提供了一种有效滤除1 / f 噪声的方法: 在对1 / f 噪声初步分析之后选择适合的正交或双正交小波,而后分别对每一层的小波系数进行滤波,最后通过小波逆变换就可得到滤除1 /f 噪声后的有用信号序列[7,8].3. 基于提升小波变换和维纳滤波的1 /f噪声滤波方法3. 1. 1 / f 噪声功率谱参数的估计为了利用基于小波变换的方法滤除1 / f 噪声,需要首先估计噪声的功率谱参数.对( 1 ) 式取对数,( 2)从( 2) 式中可见当电流I 是定值时lg[Sf( ω) ]与lgω之间是线性函数关系,通常都是用传统的最小二乘法进行直线拟合以获得γ等参数[1,7].然而,最小二乘法缺乏鲁棒性,这是因为它是基于残差是独立且正态分布这样一个假设,即使存在少量残差较大且不遵从正态分布的数据,也会导致拟合的直线与实际情况不符.不同于传统的最小二乘法,重新加权迭代最小二乘法( IRLS ) 受离群点的影响较小[9,10]. IRLS 的原理是对残差ri的平方加权wi使得Σ r2iwi最小.为了使直线拟合的结果对原始数据中的离群点具有鲁棒性,IRLS 需要选择合适的权函数.由于实际信号中不可能仅存在1 / f 噪声,当频率稍高一些时半导体器件中还会有较显著的白噪声和g-r 噪声,这将导致lg[Sf( ω) ]随着lgω的增大而弯曲,此外还可能有固定频率的干扰,并且还可能由于采集信号所用的模数转换器的采样精度不够高或者量化精度不够高导致lg[Sf( ω) ]曲线上会出现很多尖锋.基于上述分析,本文选用Tukey 重加权函数[11]式中hi是来自于最小二乘拟合的平均值函数,d 设定为4. 685,r s由残差绝对值的中值除以一个常数计算,即常数0. 6745 使IRLS 对正态分布的估计无偏.在IRLS 中,每个残差的平方都乘以一个在每次迭代中不断变化的权值,这个权值决定了每一对原始数据( lgω,lg[Sf( ω) ]) 对最终直线拟和结果的影响.如( 3) 式所示,Tukey 重加权函数赋以距离估计直线最近的数据点以最大的权重,而对距离估计直线较远的数据点则赋以较小的权重( 甚至能够取0) ,这就使得离群点对直线拟和结果的影响随着迭代次数的增加越来越小.3. 2. 提升小波变换Sweldens[12 ,13]提出了一种提升格式的小波构造方法,并且已经证明所有传统的第一代小波都可以采用提升的方法构造出来.与以傅里叶变换为基础的第一代小波变换相比,提升小波变换具有以下优点: 1 ) 提升小波变换提供了一种实现离散小波变换的快速算法,比计算第一代小波变换的Mallat 算法运算量减少一半;2 ) 逆小波变换的实现非常简单和快速;3 ) 易于实现整数小波变换.正是由于这些优点,使得提升小波变换在高速数字信号或图像处理、嵌入式和低功耗设备应用中有广阔的应用空间.设输入信号序列x( n)由两部分组成,即x( n) = u( n) + f( n) , ( 5)式中u( n) 表示有用信号,f( n) 表示1 / f 噪声,则计算x( n) 的第一层提升小波变换有三个步骤: 分解、预测和更新.1) 分解: 将输入信号x( n) 分成偶序列xe( n)和奇序列xo( n) .2) 预测: 将偶数序列xe( n) 作为奇序列xo( n)的预测值,则细节序列d1( n) 就是奇序列和预测值之间的差d1( n) = xo( n) - P( xe( n) ) , ( 6)式中P(·) 表示预测算子.3) 更新: 为了使近似信号s1( n) 能保持原信号x( n) 的某些性质,用细节序列d1( n) 来更新:s1( n) = xe( n) + U( d1( n) ) , ( 7)式中U(·) 表示更新算子.对于选定的小波,将其对应的分解和重建滤波器用多项矩阵表示,然后根据Laurent 多项式的Euclidean 算法得到计算中用到的预测算子P(·) 和更新算子U(·) [12,13].如果需要进行多层小波变换,将前一层变换获得的近似信号作为当前层的输入序列即可,如图1 所示.3. 3. FIR 型维纳滤波器的设计1 / f 噪声序列经提升小波变换得到多层系数,每一层的小波变换系数都可视为白噪声,Zhao 等[14]采用直接对小波系数限定阈值的消噪方法,在这个方法中需要根据信号和噪声的特点选择适合的阈值,而阈值的选择不能自动进行.考虑到维纳滤波是在最小均方误差准则下的最优线性滤波器,本文将其用于对小波变换系数的滤波.如图1 所示,利用FIR 型维纳滤波器对每一层的小波变换系数滤波.以第一层为例,FIR 型维纳滤波器的输入为细节序列d1( n) ,输出信号为d'1( n) ,设滤波器的学习文档 仅供参考冲击响应序列为{ g1d( n) ,n = 0,1,…,q - 1} ,则d'1( n) 由下式计算:式中r1d( 0) ,r1d( 1) ,…,r1d( q - 1) 是d1( n) 的自相关函数:4. 实验分析本文提出的1 / f 噪声滤波方法在用于微创外科手术机器人的力传感器中得到了应用. 具备力感知功能的四自由度微创外科手术机械手如图2 所示,机械手通过右端的快换接口安装在微创外科手术图1 基于提升小波变换和维纳滤波的1 / f 噪声滤波方法机器人的机械臂末端,机械手中部是外径10 mm,长约500 mm 的空心金属圆杆,手术开始时机械手经开在患者腹部的通道插入体内,由机械手左端钳形工具夹持手术针或其他微型器械完成整个手术,钳形工具的动力来源于安装在圆杆内的丝传动系统.为了测量手术过程中钳形工具与患者内脏组织的接触力,将应变片阵列布置在圆杆外表上靠近钳形工具的位置.用于应变信号调理( 包括调零、37400倍的放大、低通滤波和以TMS230F2806 型数字信号处理器为核心的数字电路) 的电路板密封在机械手右端的快换接口盒内,受到体积和功耗的严格限制,放大电路设计为二级直流放大,这就不可防止地将半导体器件产生的1 / f 噪声引入到应变信号中,并且二者的频带互相交叠.二级直流放大均选择常用的仪表放大器AD8221,AD8221 基于传统三运放的拓扑结构,具有低电压失调、低增益漂移和低噪声( 输入电压噪声为 8nV / 槡Hz) 的特点,模拟电路输出信号中的1 / f 噪声大部分来源于AD8221.为了减小电源噪声的影响,在机械臂上安装可充电镍氢电池组为整个信号调理电路供电.在传感器的初始化阶段,微创外科手术机械手还未进入工作状态,应变信号调理电路的输出可视为噪声.以1000 Hz 的采样频率和15 s 的采样时长获得一段噪声序列,图3 给出了根据该噪声序列估计的功率谱( 横轴是对数刻度) ,从图中可见在低频段功率谱和频率的函数关系接近线性,图中的虚线和点划线就是分别利用IRLS 和最小二乘法对频率小于50 Hz 的数据点进行拟合的结果,显然IRLS 拟合的直线更合理,而最小二乘法的拟合结果受功率谱曲线上的尖锋影响大一些.从IRLS 拟合直线的斜率得到γ = 2. 0.考虑到小波的消失矩R 应满足R >γ /2,即R > 1,本文选择消失矩为2 的Db 2 小波.图3 噪声的功率谱曲线图4( a) 给出了传感器进入工作状态之后采集的160s 数据,造成图中信号中部凸起的原因学习文档 仅供参考是给微创外科手术机械手的末端加载了一个0. 02 kg 的砝码( 上升沿表示加载,下降沿表示卸载) . 图4 ( b)是直接利用维纳滤波器对图4 ( a) 所示的信号处理的结果,由于1 / f 噪声的持久相关性,这种滤波器的效果不够好. 利用提升小波变换对图4( a) 所示的信号进行了八层分解,取维纳滤波器的参数q = 4,按照( 9) 式对每一层的小波变换系数设计了维纳滤波器以及相应的全通滤波器,图5 ( a) 和( b) 是对三层小波变换系数设计的维纳滤波器的幅频和相频曲线,图5( c) 是将该维纳滤波器和全通滤波器级联后的群延迟,从图中可见群延迟很接近常数6. 为了得到最优的全通滤波器,图6 给出了全通滤波的阶数v 和群延迟E 取不同值时的残差RES ,当v = 7以及E = 4 时RES 取得最小值1. 02.图4( c) 给出了经本文提出的方法处理后的信号,从图中可以看出信噪比得到了有效提升. 经过多次加载砝码的测试,最终传感器的测力分辨力不大于0. 09 N; 如果不采用任何滤波方法,传感器的测力分辨力不大于0. 12 N .图4 ( a) 原始信号; ( b) 经维纳滤波后的信号; ( c) 经本文提出的方法处理后的信号图5 ( a) 维纳滤波器的幅频响应; ( b) 维纳滤波器的相频响应;( c) 维纳滤波器和全通滤波器级联后的群延迟图6 最优全通滤波器的选择5. 结论本文针对半导体器件中普遍存在的1 / f 噪声提出了一种结合了提升小波变换和维纳滤波器的处理方法.这种方法需要首先利用重新加权迭代最小二乘法拟合1 / f 噪声的功率谱曲线并估计噪声参数,而后选择恰当的分析小波.这种处理方法包括三个过程: 1) 提升小波分解; 2) 滤波: 考虑到小波变换对1 / f 噪声的白化作用,利用维纳滤波器对每一层小波系数进行处理.设计了最优全通滤波器以校正维纳滤波器的相频特性,使得小波系数经滤波后相位不变; 3 ) 提升小波重构.在用于微创外科手术机器人的力传感器上进行的实验说明提出的方法能够有效抑制1 / f 噪声,并使传感器的分辨力提高了25% ,同时也为分析和检测半导体器件的1 / f 噪声提供了实验依据.[1] Zhang Z G,Guo S X,Gao F L,Yu S Y,Li X Y 2009 ActaPhys. Sin. 58 2772 ( in Chinese) [张振国、郭树旭、郜峰利、于思瑶、李雪妍2009 物理学报58 2772][2] Bao J L,Zhuang Y Q,Du L,Li W H,Wan C X,Zhang P 2005Acta Phys. Sin. 54 2118 ( in Chinese) [包军林、庄奕琪、杜磊、李伟华、万长兴、张萍2005 物理学报54 2118][3] Liu Y A,Du L,Bao J L 2008 Acta Phys. Sin. 57 2468 ( inChinese) [刘宇安、杜磊、包军林2008 物理学报57 2468][4] Lin L Y,Du L,Bao J L,He L 2011 Acta Phys. Sin. 60 047202( in Chinese) [林丽艳、杜磊、包军林、何亮2011 物理学报60 047202][5] Zhuang Y Q,Sun Q 1993 Noise and its Minimizing Technology inSemiconductor Devices ( Beijing: National Defense Industry Press) pp80—128 ( in Chinese) [庄奕琪、孙青1993 半导体器件中的噪声及其低噪声化技术( 北京: 国防工业出版社) 第80—128 页][6] Tewfik A H,Kim M 1992 IEEE Trans. Inform. Theory 38 904[7] Ninness B 1998 IEEE Trans. Inform. Theory 44 32[8] Atto A M,Pastor D,Mercier G 2010 IEEE Trans. Inform.Theory 56 4741[9] Jabr R A 2006 Int. J. Elec. Power 28 86[10] Fomenko I,Durst M,Balaban D 2006 Comput. Meth. Prog.Bio. 82 31[11] Hund E,Massart D L,Smeyers-Verbeke J 2002 Anal. Chim.Acta 463 53[12] Sweldens W 1996 Appl. Comput. Harmon. A 3 186[13] Sweldens W 1998 SIAM J. Math. Anal. 29 511[14] Zhao Z H,Zhang Y H,Jiang H 2002 J. Shanghai Jiaotong Univ. 36 1037 ( in Chinese) [赵忠华、张炎华、江红2002 上海交通大学学报36 1037]学习文档仅供参考。

基于小波变换的噪声消除的方法作者:罗俊来源:《硅谷》2009年第15期[摘要]介绍小波变换的一般理论及在信号降噪应用中的理论基础,分析染噪后语音信号的特性,并使用多种小波和不同阈值对语音信号进行小波变换降噪,对结果进行分析比较。
[关键词]小波变换信号降噪 MATLAB实现中图分类号:TN92文献标识码:A文章编号:1671-7597(2009)0810019-01语音的传输在多媒体通信、数字音频广播中占有非常重要的地位;而语音在信道中的传输总会伴随着一定的噪声,这不仅损害了语音的质量,严重时还会干扰语音的正常接收。
所以,语音信号的降噪是语音传输过程中必须解决的一个重要问题。
传统的降噪方法是将接收到的混合信号进行傅里叶变换,去除掉高频成分(噪声),保留低频成分(有用信号),然后再做逆变换,恢复信号。
这样虽然能去掉噪声,但同时也把有用信号中的高频信息丢失了,产生了高频失真。
小波变换是一种信号的时间-尺度(时间-频率)分析方法,它具有多分辨率分析(Multiresolution Analysis)的特点,而且在时频两域都具有表征信号局部特征的能力,是一种窗口大小固定不变但形状改变的时频局部化分析方法。
即在低频部分具有较高的频率分辩率和较低的时间分辩率,在高频部分具有较高的时间分辩率和较低的频率分辩率,很适合于探测正常信号中夹带的瞬态反常现象并展示其成分,所以小波变换用于语音信号的消噪是近年来比较热门的方法。
一、小波变换理论概述小波是一种特殊的长度有限,平均值为0的波形。
它有两个特点:一是在时域都具有紧支集或近似紧支集;二是正负交替的“波动性”,也即直流分量为零。
小波分析是将信号分解成一系列小波函数的叠加,这些小波函数都是同一个母小波函数经过平移与尺度伸缩得来的,用不规则小波函数来逼近尖锐变换的信号显然要比光滑的正弦曲线要好。
小波变换主要有以下特点:1.具有多分辨率的特点,可以由粗及细地逐步观察信号;2.可以看成用基本频率特性Ψ(ω)的通带滤波器在不同尺度a下对信号做滤波。

基于小波分析的信号去噪技术[摘要] 介绍了小波变换的基本思想和优点及多分辨率分析的过程, 并在MA TLAB 下利用小波变换工具箱, 编写程序实现信号去噪处理。
充分显示了小波变换在处理非平稳信号中的优势。
[关键词] 小波变换 信号去噪 模极大值 李普西兹指数在通信及计算机过程控制系统中,对信号进行实时采样是很重要的环节。
但由于信号在激励、传输和检测过程中,可能不同程度地受到随机噪声的污染,特别在小信号采集和测量中,噪声干扰显得尤其严重。
因此,如何消除实际信号中的噪声,从混有噪声的信号中提取有用信息一直是信息学科研究的焦点之一。
傅里叶变换是一种经典方法,适用于诸多场合。
但由于傅里叶变换是一种全局变换,无法表述信号的时域局部性质,而这种性质恰恰是非平稳信号最根本和最关键的性质。
为了更有效地处理非平稳信号,人们提出了小波变换这种新的信号分析理论。
小波变换是一种信号的时频分析,它具有多分辨率的特点,可以方便地从混有强噪声的信号中提取原始信号,被誉为分析信号的显微镜。
本文主要讨论应用小波变换的理论,利用Matlab 软件在计算机上实现了信号的噪声消除,从混有噪声的实际信号中提取了原始信号,具有非常实用的意义。
1.小波变换与多分辨率分析设ψ是定义在(-,+)∞∞上能量有限的函数,Ψ构成平方可积信号空间,记为Ψ∈L2(R),则生成函数族{ab ψ }: 1/2()||()ab t b t a a --ψ=ψ ,0b a -∞<<+∞> (1)Ψ(t)称为小波函数,()ab t ψ由Ψ(t)伸缩和平移生成,为小波基函数。
a 为伸缩因子,b 为平移因子。
对任一信号()f i ∈L2(R)的连续小波变换可定义为信号与小波基函数的内积:1/2(();,),||()ab R t b WT f t a b f a dt a --=<ψ>=ψ⎰ (2)连续小波变换具有线性、平移不变性、伸缩共变性、自相似性和冗余性等重要性质。

基于小波分析的信号去噪一、实验目的1、掌握小波分析的原理;2、利用小波分析进行信号去噪,并编写Matlab 程序。
二、实验内容1、使用不同小波函数对信号去噪,比较消噪效果;2、采取不同分解层数对信号去噪,比较消噪效果;3、阈值设定方法对信号去噪的影响;三、实验原理小波分析方法是一种窗口大小(即窗口面积)固定但其形状可改变,时间窗和频率窗都可改变的时频局部化分析方法。
即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,所以被誉为数学显微镜。
正是这种特性,使小波变换具有对信号的自适应性。
原则上讲,传统上使用傅里叶分析的地方,都可以用小波分析取代。
小波分析优于傅里叶变换的地方是,它在时域和频域同时具有良好的局部化性质。
小波函数的定义:设()t ψ为平方可积函数,即())(2R L t ∈ψ,若其傅里叶变换()ωψ∧(()ωψ∧是()t ψ的傅里叶变换)满足∞<=⎰∧ωωωψψd C R 2)( 称()t ψ为一个基本小波或母小波(Mother Wavelet ),并称上式为小波函数的允许条件。
与标准的傅立叶变换相比,小波分析中用到的小波函数不具有唯一性,对于一个时频分析问题,如何选者最佳的小波基函数是一个重要的问题。
常用的小波函数有Haar 小波、dbN 小波、Morl 小波、Mexh 小波、Meyer 小波等,不同的小波函数对应不同的尺度函数和性能。
从下图中可以看出小波变换与傅立叶变换在时频窗口特性上有很大的不同,更显示了上述小波变换的特点。
图6-1 小波变换的时频分析窗小波变换的多分辨率分析实际上就是对一个频带信号进行低频分解,对每一步分解出来的低频部分在分解,使频率分辨率越来越高,其目的是构造一个理想的正交小波基。
小波包分析实际上就是对与多分辨率分析没有分解的高频信号也进行逐层分解,进一步提高时频分辨率。
小波分析地这些原理与特点与测控领域中的滤波原理非常相似,常常被用于信号噪声的消除。

小波变换方法消除热重实验噪音信号郁青春1) 张世超2) 王新东1)1)北京科技大学冶金与生态学院,北京100083 2)北京航空航天大学材料科学与工程学院,北京100083摘 要 由于受实验条件的影响,在用等温热重法进行稀土氧化物脱除烟气中SO 2的动力学实验过程中有噪音信号的干扰,因而采用Daubechies (N =3)小波函数和Matlab 软件讨论了小波变换方法消除热重实验噪音信号的影响因素.研究发现阀值的选取规则和软硬阀值处理方式对消除噪音信号的影响不大,分解层数则对消除噪音信号的影响较大.当信噪比变化平缓时所对应的分解层数是最佳分解层数.经Daubechies (N =3)小波函数消噪后得到的信号能够比较真实地反映等温热重实验的动力学过程.关键词 稀土氧化物;脱硫;热重分析法;去噪;小波变换分类号 TP 391;X70113收稿日期:2006201208 修回日期:2006205222基金项目:国家自然科学基金资助课题(No.90210003);北京市自然科学基金资助课题(No.2012010)作者简介:郁青春(1971—),男,博士研究生;张世超(1963—),男,教授 热重分析是指在程序控制温度下测量物质的质量变化与温度关系的一种技术,通常又称之为热重法(TG )[1-2].同属于热重分析范围的还有等温质量变化测定、等压质量变化测定、溢出气体监测、微商热量法等,这些方法都是在热重法基础上略加变动和控制而发展起来的.其中等温质量变化测定可以看作热重法在控温程序为“恒温”时的一种特例,该法在进行等温动力学分析时经常被采用.对于稀土氧化物脱除烟气中SO 2来说,采用等温热重实验进行研究是很重要的实验手段.由于受到实验仪器、实验条件等其他因素的影响,使测得的热重曲线失真,因此消除热重实验的噪音信号对于保证实验正常进行具有重要意义.对于含有噪声的信号滤波方法,常用的有滑动平均法、曲线拟合法、样条函数拟合法、Fourier 变换法等.这些滤波方法可以认为是根据信号的特征设计最佳的低通滤波器.小波变换是近年发展起来的一门新的数学分支,属于时频分析,小波函数由于具有良好的时频分辨能力而成为信号处理的一种强有力的工具[3].本文采用了小波变换方法来消除热重实验中的噪音信号.1 小波变换消噪的思想111 小波变换[4]假设带分析信号f (x )为能量有限的一维函数,f (x )∈L 2(R ),则连续小波变换定义为:Wf (a ,b )=1a ∫Rf (x )ψx -bad x (1)式中,a 称为尺度因子,b 为平移因子,R 为时域,ψ(x )称为母小波,a 为归一化因子.ψ(x )存在逆变换须满足的条件为:设ψ(x )的傅里叶变换为ψ(ω),则∫R |ψ(ω)|2ωd ω<∞(2)这时,称ψ(x )为小波函数.小波变换的逆变换公式为:f (x )=1c∫+∞0Wf (a ,b )=1aψx -a bd b (3)其中,c =∫+∞|ψ(aω)|2ad a <∞(4)可以进行信号重构.112 小波变换的消噪原理[5]一个含噪的一维信号模型可表示为如下形式:s (i )=f (i )+σe (i ) i =0,…,n -1(5)其中,s (i )为含噪信号,f (i )为真实信号,σ为噪声系数,e (i )为噪音信号,i 为采样时间点.为了从含噪信号s (i )中还原出真实信号f (i ),可以利用信号和噪声在小波变换下的不同特性,通过对小波分解系数进行处理来达到信号和噪声分离的目的.在实际工程中,有用信号通常表现为低频信号或是一些比较平稳的信号,而噪声信号则表现为高频信号.小波变换可以将信号多层分解,如图1所示.图中S 为原始信号,cA 1、cA 2和cA 3为分解后的低频部第29卷第5期2007年5月北京科技大学学报Journal of U niversity of Science and T echnology B eijingV ol.29N o.5May 2007分,cD 1、cD 2和cD 3为分解后的高频部分,下标1,2和3分别代表分解的层次.分解具有关系:S =cA 3+cD 3+cD 2+cD 1.可以看出,如要进行进一步的分解,则可以将低频部分cA 3分解为低频部分cA 4和高频部分cD 4,以下再分解依次类推.图1 小波分解图Fig.1 Diagram of decomposition of a w avelet利用门限阀值等形式对高频小波系数进行处理,然后重构,即可达到消噪的目的.对信号消噪实质上是抑制信号中的无用部分,恢复信号中的有用部分的过程.113 小波基的选取[6]Daubechies 小波系是由法国学者Daubechies 提出的一系列二进制小波的总称,MA TLAB 中记为db N ,N 为小波的序号,由于它易于实现快速算法而被普遍关注.Daubechies 小波基系列定义为:假设存在p (y )=∑n -1k =0Cn -1+k ky k(6)则|m 0(ω)|2=cos 2ω2nP sin2ω2(7)其中,C n -1+kk 是二项式系数,m 0=12∑2n -1k =0h k e -i k ω.Daubechies 小波基系列由系数C μn 来确定尺度函数Φ(x )和小波函数ψ(x ),二者长度均为2n -1,其中μ取近似值012.不同的小波基的表现形式是不同的.小波基的选用主要考虑以下几个方面:(1)小波基函数连续;(2)必须有足够的消失矩;(3)便于实现离散算法.经过多次优化编程计算比较,采用db3小波满足测量要求.db3小波函数如图2所示.2 结果与讨论211 处理前的热重信号图3是热重实验直接得到的原始信号.从图中可以看出:大约300s 左右质量开始有变化,说明此时开始有反应发生;随着反应时间的延长,质量趋于稳定,说明反应接近结束.另外从图中可以发现一种随机的噪音信号自始至终都伴随着热重信号,该噪音信号平稳,没有较大的波动,是典型的平稳噪音信号.该噪音来源是热重实验中AD 转换及实验温度、气体流量等因素造成的,由于这些因素在实验过程中保持恒定,体现在热重信号中便是一种平稳的随机噪音信号.图2 Daubechies (N =3)小波函数Fig.2 W avelet function of Daubechies (N =3)图3 原始热重信号Fig.3 Original thermogravimetric signal212 不同阀值对消噪的影响[7]图4是采用Minimaxi 、Sqtwolog 和Heursure 阀值选取规则和db3小波函数分解4层后得到的信号.通过对比发现Minimaxi 阀值规则和Sqtwolog 阀值规则得到的去噪曲线大致相同,两者都能较多地保留原始信号的特点;Heursure 阀值规则去噪后的信号略微比其他两种阀值规则光滑一点,但不是很明显.说明阀值的选取对热重信号消噪不产生较大的影响.213 分解层数的影响[8]图5是采用db3小波函数处理后的信号.信号低频部分代表着信号的发展趋势,随着分解层数的增加,信号高频噪音信号随之减少,热重曲线的变化趋势更加明显.这表明通过小波变换的方法可以将热重曲线的基本形状反映出来.一般来讲,所有来辨识的信号本身不能有很大的突变,这是因为信号的发展趋势是由信号的低频部分所表征的.如果在信号本身中包含有很大的突变,那么在小波变换的·335·第5期郁青春等:小波变换方法消除热重实验噪音信号图4 不同阀值选取规则去噪.(a)Minim axi;(b)Sqt w olog;(c)H eursureFig.4 Denoising signals with different rules of threshold :(a )Minim axi;(b)Sqt w olog;(c)H eursure低频部分中,显示出来的信号会和原始信号有很大的差别,因为小波变换会将信号本身的突变当作高频部分给滤掉了.在图6的d6已经反映出信号在400s 左右突变的特征,说明已经有一部分低频信号给滤掉了;但是在图5中a6的近似图上没有明显体现出来,一直到a8近似层才明显看到已经有部分信号失真了.因而在实际应用中信号的分解层数不是越多越好.为了定量地说明分解层数对信号的影响,对采用db3小波函数不同分解层数的信噪比进行了计算.当分解层数为1~9时,信噪比分别为:28125,24125,22100,20191,20142,20113,19183,18167,13122.可以看出:随着分解层数的增加,信噪比显著降低,这是由于把噪音信号分离出去所致;但到达顶层数后信噪比变化平缓,此时大部分噪音已经分离出,再增加分解层数对噪音的分离效果已经不起图5 原始信号和各层近似Fig.5 Original signal and its approxim ations with different de 2compositionlayers图6 原始信号和各层细节Fig.6 Original signal and its details with different decomposition layers·435·北 京 科 技 大 学 学 报第29卷主要作用;之后,随分解层数增加,信噪比又显著增加,说明此时已经把部分低频信号当作高频噪音去除.合适的分解层数应该是在信噪比变化比较平缓的时刻所对应的分解层数.针对信噪比变化平缓的分解层数,分别作了分解层数是6,7和8时的信号处理曲线,如图7所示.分解层数以7层最佳,8层已经明显看到曲线失真了.图7 不同分解层数消噪信号.(a)6;(b)7;(c)8Fig.7 Denoisingsignals at different decomposition layers with db3:(a)6;(b)7;(c)8214 阀值处理方式的影响对阀值的应用可以采用软阀值或者硬阀值两种方式.软阈值法:进行趋零处理,算子D 将数据域U 中所有|U |≤λ的数值置为零,并对|U |>λ的数值以量λ缩小,它将不置为0的那些系数值进行趋零处理.硬阈值法:进行截断处理,若|U |>λ,则保留;否则置为0[9].一般来讲采用硬阀值处理的信号与采用软阀值处理的信号相比,仍有少量毛刺,信号波形较粗糙,采用软阀值处理的信号波形形状好,比较平缓.图8分别是db3小波函数7层分解采用软硬阀值处理方式后的信号.从图8可以看到软硬阀值的选取似乎对热重信号处理的影响不是很大,这可能是与该热重信号和噪音信号都比较平缓所致.图8 不同阀值消噪方式信号.(a)软阀值;(b)硬阀值Fig.8 Denoising signals with different methods of threshold :(a)soft threshold;(b)h ard threshold3 结论(1)阀值的选取规则对消除热重信号的噪音信号影响不大.(2)软阀值和硬阀值的不同处理方式对消除热重信号的噪音信号影响不大.(3)信号的分解层数对消除热重信号的噪音信号影响较大,当信噪比变化平缓时分解层数最佳.实验表明用db3小波函数消除热重信号的噪音信号,其最佳分解层数为7.参 考 文 献[1] 周静,龚欣,于遵宏.煤焦二氧化碳气化动力学研究.煤炭转化,2003,26(1):78[2] 胡晓静,盛向军,赵恒英,等.热重量法分析石墨成分.理化检验化学分册,2003,38(9):443[3] 郑忠龙,于飞,刘喜梅,等.应用小波分析研究信号消噪.青岛化工学院学报,2002,23(4):71[4] 王仲民,戴士杰.基于小波变换的信号消噪.河北工业大学学报,2000,29(5):48[5] 董小刚,秦喜文.信号消噪的小波处理方法及其应用.吉林师·535·第5期郁青春等:小波变换方法消除热重实验噪音信号范大学学报:自然科学版,2003,24(2):13[6] 井文才,李强,任莉,等.小波变换在白光干涉数据处理中的应用.光电子·激光,2005,16(2):195[7] 胡松,孙学信,熊友辉.小波分析在热重实验数据处理中的应用.化工学报,2002,53(12):1276[8] 邓懿波,谭志洪,黄媛.小波降噪影响因素的研究.华东交通大学学报,2005,22(2):161[9] 林克正,李殿璞.基于小波变换的去噪方法.哈尔滨工程大学学报,2000,21(4):21 Denoising of thermogravimetry signal by wavelet transformY U Qi ngchun 1),ZHA N G S hichao 2),W A N G Xi ndong 1)1)Metallurgical and Ecological Engineering School ,University of Science and Technology Beijing ,Beijing 100083,China 2)School of Material Science and Engineering ,Beijing University of Aeronautics and Astronautics ,Beijing 100083,ChinaABSTRACT There exists noise signal in the kinetic experiment of desulfurization of flue gas with rare earth ox 2ides by means of isotherm thermogravimetry because of experimental conditions.The contributing factors of thedenoising of thermogravimetric signal were discussed by the Daubechies (N =3)function of wavelet transform and Matlab software.The results showed that different rules of threshold and methods of threshold have little effect on denoising ,but the number of decomposition layers play an important role in denoising.The optimal number of decomposition layers could be obtained when the rate of signal to noise changed slow.The signal rep 2resented the kinetics process of the isotherm thermogravimetric experiment truly after denising.KE Y WOR DS rare earth oxides ;sulphur dioxide ;thermogravimetry ;denoising ;wavelet transform·635·北 京 科 技 大 学 学 报第29卷。


基于小波变换的噪声消除算法研究在电工和电子技术实验中,需要对各种参数进行测量,但由于电磁噪声的存在直接影响了测量的结果,有时甚至会将有用信号完全淹没而导致测量失败。
本文以小波变换为基础,对消除测量信号中的白噪声方法进行了研究,以求达到合理消除白噪声的目的。
1小波消噪的原理一般地,有用信号通常表现为低频信号或是一些比较平稳的信号,而噪声信号则通常表现为高频信号。
所以消噪过程主要进行以下处理:首先对原始信号进行小波分解,则噪声部分在电工和电子技术实验中,需要对各种参数进行测量,但由于电磁噪声的存在直接影响了测量的结果,有时甚至会将有用信号完全淹没而导致测量失败。
本文以小波变换为基础,对消除测量信号中的白噪声方法进行了研究,以求达到合理消除白噪声的目的。
1 小波消噪的原理一般地,有用信号通常表现为低频信号或是一些比较平稳的信号,而噪声信号则通常表现为高频信号。
所以消噪过程主要进行以下处理:首先对原始信号进行小波分解,则噪声部分通常包含在高频系数中;然后对小波分解的高频系数以门限阈值等形式进行量化处理;最后再对信号重构即可达到消噪的目的。
对信号消噪实质上是抑制信号中的无用部分,恢复信号中有用部分的过程。
设一个含噪声的一维信号的模型可以表示成如下形式:s(i)=f(i)+σ·e(i), i=0,1,…,n-1其中,f(i)为真实信号,e(i)为噪声,s(i)为含噪声的信号。
一般来说,一维信号的降噪过程可分为一维信号的小波分解,小波分解高频系数的阈值量化处理和一维小波的重构3个步骤。
小波能够消噪主要由于小波变换具有如下特点:低熵性小波系数的稀疏分布,使图像处理后的熵降低。
多分辨特性由于采用了多分辨的方法,所以可以非常好地刻画信号的非平稳性,如突变和断点等,可以在不同分辨率下根据信号和噪声的分布来去除噪声。
去相关性小波变换可对信号去相关,且噪声在变换后有白化趋势,所以小波域比时域更利于去噤。
基函数选择更灵活小波变换可以灵活选择基函数,也可以根据信号特点和降噪要求选择多带小波、小波包等,对不同的场合,可以选择不同的小波基函数。
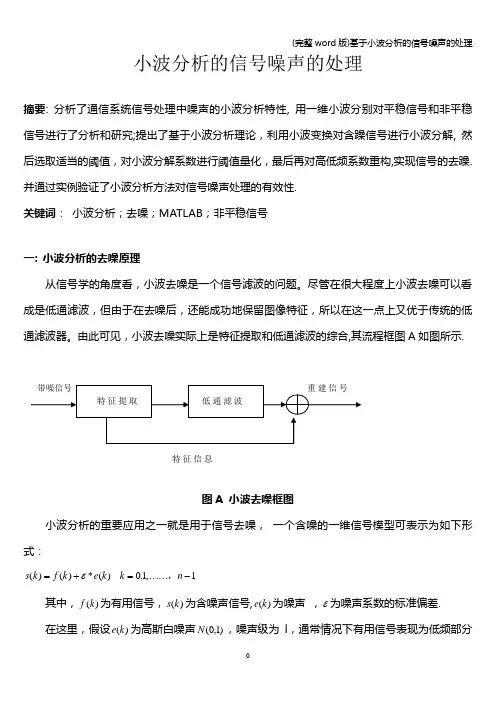
小波分析的信号噪声的处理摘要: 分析了通信系统信号处理中噪声的小波分析特性, 用一维小波分别对平稳信号和非平稳信号进行了分析和研究;提出了基于小波分析理论,利用小波变换对含躁信号进行小波分解, 然后选取适当的阈值,对小波分解系数进行阈值量化,最后再对高低频系数重构,实现信号的去躁.并通过实例验证了小波分析方法对信号噪声处理的有效性.关键词: 小波分析;去噪;MATLAB ;非平稳信号一: 小波分析的去噪原理从信号学的角度看,小波去噪是一个信号滤波的问题。
尽管在很大程度上小波去噪可以看成是低通滤波,但由于在去噪后,还能成功地保留图像特征,所以在这一点上又优于传统的低通滤波器。
由此可见,小波去噪实际上是特征提取和低通滤波的综合,其流程框图A 如图所示.图A 小波去噪框图小波分析的重要应用之一就是用于信号去噪, 一个含噪的一维信号模型可表示为如下形式:)(*)()(k e k f k s ε+= 1,1,0-⋯⋯=n k ,其中,)(k f 为有用信号,)(k s 为含噪声信号,)(k e 为噪声 ,ε为噪声系数的标准偏差. 在这里,假设)(k e 为高斯白噪声)1,0(N ,噪声级为l,通常情况下有用信号表现为低频部分特征信息或是一些比较平稳的信号,而噪声信号则表现为高频的信号,下面对S (k )信号进行如图B结构的小波分解,则噪声部分通常包含在C d l 、C d 2 、C d 3 中,只要对C d l ,C d 2 , C d 3作相应的小波系数处理, 然后对信号进行重构即可以达到去噪的目的。
图B上述信号消噪的过程可分为三个步骤进行:1 )一维信号的小波分解。
选择一个小波并确定分解的层次N,然后对信号S进行N层小波分解;2 )小波分解高频系数的阈值量化。
对各个分解尺度下的高频系数选择一个阈值进行软阈值量化处理;3 ) 一维小波重构。
根据小波分解的最底层低频系数和各层高频系数进行一维小波重构。
在这3个步骤中, 最关键的是如何选择阈值及如何进行阈值量化,在某种程度上,它关系到信号消噪的质量。
基于小波变换的信号去噪技术研究近年来,信号处理技术在各个领域中扮演着越来越重要的角色。
在传统的信号处理方法中,一般利用滤波器等手段进行去噪处理。
然而,这种方法存在很多不足,例如难以处理多变的噪声,也容易出现误判等问题。
随着小波变换技术的不断发展,基于小波变换的信号去噪技术正逐渐成为一种有效的替代方法。
小波变换在信号处理中具有许多优点,能够有效地提取信号中的特征,并将其与噪声分开进行处理。
本文将会对基于小波变换的信号去噪技术进行详细探讨。
一、小波变换简介小波变换是一种最近20年内发展起来的新型信号分析方法,它具有许多传统傅里叶变换所不具备的特性。
小波变换可以将信号分成低频和高频两部分进行处理,这种能够提供更加细致的信号分解能力,使得信号的特征更加明显。
此外,小波变换还能够适应信号的现实特性,更好地适用于一些特定的应用。
二、小波去噪方法小波去噪方法是基于小波变换所开发而来的,其主要思路是通过多级小波变换将原始信号分解成不同尺度下的子带信号,再通过对每个分解出来的子带信号进行阈值处理,从而实现对信号噪声的去除。
具体地,小波去噪方法可分为以下三个步骤:(1)小波分解将原始信号进行多级小波分解,得到不同尺度下的子带信号。
(2)阈值处理对每个子带信号进行阈值处理,去除低于一定阈值的信息,降低噪声对原始信号的影响。
(3)小波重构将处理后的信号进行多级小波重构,得到去噪后的信号。
三、小波去噪算法小波去噪算法是指通过运用小波变换理论,将原信号去除其中混杂的噪声,实现信号的准确重构的一种算法。
其中最常用的算法分别有软阈值、硬阈值和连续小波变换。
1. 软阈值算法软阈值算法是指将小于某一特定阈值的绝对值的所有系数设为零,大于这一阈值的系数变成更小的数。
这种方法在去噪量得到充分保证的同时,可以让最终信号更加平滑。
2. 硬阈值算法硬阈值算法是指将所有绝对值小于某特定阈值的系数取零,即对所有小于固定阈值的系数进行直接处理。
这种方法相对MSE的处理方法容易使得处理后的信号比较平稳,但同时误差较大。
基于小波变换的语音信号去噪净化实现研究的开题报告一、研究背景与意义语音信号是人类重要的沟通方式之一,但在实际中,许多语音信号都存在噪声干扰。
这些噪声不仅会影响语音的质量,也会干扰语音识别的准确率,因此语音信号去噪净化技术具有重要的研究意义。
小波变换是一种广泛应用于语音信号处理的有效工具,可以将信号分解为高频和低频成分,提取信号的本质特征。
因此,基于小波变换的语音信号去噪净化方法是一种值得研究的技术。
二、研究内容与方法本文将研究基于小波变换的语音信号去噪净化方法。
具体研究内容包括以下几个方面:(1)对语音信号进行小波分解,得到高频和低频成分。
(2)利用小波分析特性来选择合适的小波基函数和阈值处理方法。
(3)对高频成分进行阈值处理,去除噪声信号。
(4)对低频成分进行加权平均并重构信号。
(5)比较本文提出的方法与其他去噪方法的效果,验证方法的有效性。
研究方法主要包括以下几个步骤:(1)准备语音信号和噪声信号。
(2)进行小波分解和阈值处理,得到去噪后的语音信号。
(3)利用评价指标来比较本文提出的方法和其他去噪方法的效果。
(4)通过实验来验证方法的有效性。
三、研究目标与意义本文旨在提出一种基于小波变换的语音信号去噪净化方法,对语音信号进行处理,去除其中的噪声信号,从而提高语音信号的质量和识别准确率。
本研究的意义在于:(1)提出一种新的语音信号去噪净化方法,具有一定的创新性。
(2)通过实验验证所提出方法的有效性。
(3)为语音信号去噪净化方向的研究提供参考。
四、预期结果通过本文研究,预计可以得到以下几个结果:(1)提出一种基于小波变换的语音信号去噪净化方法。
(2)通过实验验证所提出方法的有效性。
(3)得到比较好的去噪净化效果,提高语音信号的质量和识别准确率。
五、研究计划1. 第一阶段(2周)a. 确定研究方向,阅读相关文献b. 熟悉小波变换的基本理论和相关知识2. 第二阶段(4周)a. 对语音信号进行小波分解,得到高频和低频成分b. 选择合适的小波基函数和阈值处理方法3. 第三阶段(4周)a. 对高频成分进行阈值处理,去除噪声信号b. 对低频成分进行加权平均并重构信号4. 第四阶段(4周)a. 比较本文提出的方法与其他去噪方法的效果b. 验证方法的有效性5. 第五阶段(2周)a. 总结研究成果,撰写毕业论文b. 准备学术报告六、预期步骤和成果通过本文的研究,将来可以对基于小波变换的语音信号去噪净化方法进行更深入的探讨。
基于小波变换的去噪摘要:本文说明小波变换的基本原理,实现小波分解与重构的Mallat 算法以及利用小波变换去除信号噪声的方法和原理,并在Matlab 环境下进行了仿真。
关键词:小波变换; 多分辨分析; Mallat 算法; 消噪;1.引言由于信号在产生、传输和检测过程中,不可避免地会受到不同程度噪声的影响,特别是小信号,干扰显得尤为明显,因此在信号处理过程中,最重要的就是消除信号中的噪声。
对此,傅立叶分析是一种经典方法,但其无法同时描述和定位信号在时间和频率上的突变部,而小波变换具有多分辨率的特点,能表征信号局部特征,因此在信号处理中有着重要的应用。
本文主要介绍小波变换理论和去噪原理及方法,并通过MATLAB 仿真实现信号噪声消除。
2.小波变换记()t ψ,总假设()t ψ是能量有限的,即()()R L t 2∈ψ。
通过对()t ψ作平移,伸缩可以得到一族小波函数,其中a 称为尺度因子或伸缩因子,b 称为平移因子,()⎭⎬⎫⎩⎨⎧∈>⎪⎭⎫⎝⎛-=R b a a b t a t b a ,0|1,ψψ所以小波函数()t ψ又被称作为母小波。
这族函数中每一个都有规范化的函数()1,==t b a ψψ。
设()()R L t f 2∈,则()t f 的连续小波变换定义为()t f 与()t b a ,ψ的内积()()()()()()()dt a b t t f ab a Wf t t f b a Wf b a ⎪⎭⎫ ⎝⎛-==⎰∞+∞-*,1,,,ψψ 从中可以看出小波变换也是一种积分变换,它将单变量的函数()t f 变换成时频平面上的二元函数()b a Wf ,。
从时频分析来看,小波变换将信号()t f 的每个瞬态分量映射到时频平面上的位置正好对应于分量的频率和发生的时间,而函数()b a Wf ,在()b a ,处的值反映了在时刻b 频率为a1的分量的有关信息。
由()b a Wf ,到原始信号()t f ,称为逆变换或重构。