戴维南定理及应用_张巨芳

戴维南定理典型例子_戴维南定理解题方法什么是戴维南定理戴维南定理（又译为戴维宁定理）又称等效电压源定律，是由法国科学家L·C·戴维南于1883年提出的一个电学定理。

由于早在1853年，亥姆霍兹也提出过本定理，所以又称亥姆霍兹-戴维南定理。

其内容是：一个含有独立电压源、独立电流源及电阻的线性网络的两端，就其外部型态而言，在电性上可以用一个独立电压源V和一个松弛二端网络的串联电阻组合来等效。

在单频交流系统中，此定理不仅只适用于电阻，也适用于广义的阻抗。

戴维南定理在多电源多回路的复杂直流电路分析中有重要应用。

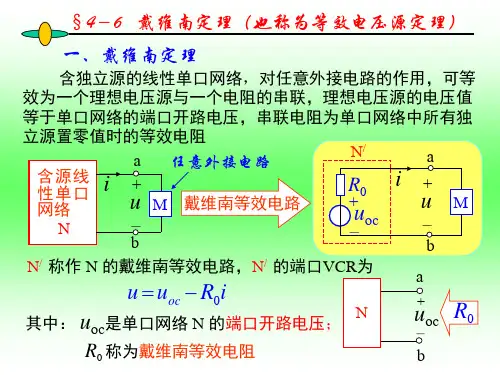
戴维南定理（Thevenin‘stheorem）：含独立电源的线性电阻单口网络N，就端口特性而言，可以等效为一个电压源和电阻串联的单口网络。

电压源的电压等于单口网络在负载开路时的电压uoc；电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。

戴维南定理典型例子戴维南定理指出，等效二端网络的电动势E等于二端网络开路时的电压，它的串联内阻抗等于网络内部各独立源和电容电压、电感电流都为零时，从这二端看向网络的阻抗Zi。

设二端网络N中含有独立电源和线性时不变二端元件（电阻器、电感器、电容器），这些元件之间可以有耦合，即可以有受控源及互感耦合；网络N的两端ɑ、b接有负载阻抗Z（s），但负载与网络N内部诸元件之间没有耦合，U（s）=I（s）/Z（s）。

当网络N中所有独立电源都不工作（例如将独立电压源用短路代替，独立电流源用开路代替），所有电容电压和电感电流的初始值都为零的时候，可把这二端网络记作N0。

这样，负载阻抗Z（s）中的电流I（s）一般就可以按下式1计算（图2）式中E（s）是图1二端网络N的开路电压，亦即Z（s）是无穷大时的电压U（s）；Zi（s）是二端网络N0呈现的阻抗；s是由单边拉普拉斯变换引进的复变量。

和戴维南定理类似，有诺顿定理或亥姆霍兹－诺顿定理。

按照这一定理，任何含源线性时不变二端网络均可等效为二端电流源，它的电流J等于在网络二端短路线中流过的电流，并联内阻抗同样等于看向网络的阻抗。

戴维南定理和诺顿定理戴维南定理（Thev enin’s theorem ）是一个极其有用的定理，它是分析复杂网络响应的一个有力工具。

不管网络如何复杂，只要网络是线性的，戴维南定理提供了同一形式的等值电路。

先了解一下二端网络/也叫一端口网络的概念。

（一个网络具有两个引出端与外电路相联，不管其内部结构多么复杂，这样的网络叫一端口网络）。

含源单口（一端口）网络──内部含有电源的单口网络。

单口网络一般只分析端口特性。

这样一来，在分析单口网络时，除了两个连接端钮外，网络的其余部分就可以置于一个黑盒子之中。

含源单口网络的电路符号：图中N ──网络 方框──黑盒子U单口松驰网络──含源单口网络中的全部独立电源置零，受控电源保留，（动态元件为零状态），这样的网络称为单口松驰网络。

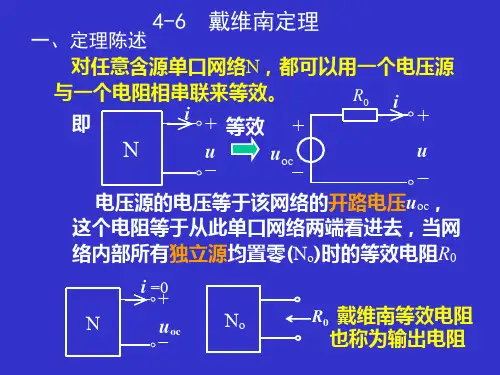
电路符号：一、戴维南定理（一）定理：一含源线性单口一端网络N ，对外电路来说，可以用一个电压源和电阻的串联组合来等效置换，此电压源的电压等于端口的开路电压，电阻等于该单口网络对应的单口松驰网络的输入电阻。

（电阻等于该单口网络的全部独立电源置零后的输入电阻）。

上述电压源和电阻串联组成的电压源模型，称为戴维南等效电路。

该电阻称为戴维南等效电阻。

U任意负载任意负载U oc =U s求戴维南等效电路，对负载性质没有限定。

用戴维南等效电路置换单口网络后，对外电路的求解没有任何影响，即外电路中的电流和电压仍然等于置换前的值。

（二）戴维南定理的证明：1. 设一含源二端网络N 与任意负载相接，负载端电压为U ，端电流为I 。

2. 任意负载用电流源替代，取电流源的电流为I I S 。

方向与I 相同。

替代后，整个电路中的电流、电压保持不变。

下面用叠加定理分析端电压U 与端电流I 。

3. 设网络N 内的独立电源一起激励，受控源保留，电流源I S 置零，即ab 端开路。

这时端口电压、电流加上标（1），有SU (1)=U ocI (1)=04. I S 单独激励，网络N 内的独立电源均置零，受控电源保留，这时，含源二端网络N 转化成单口松驰网络N 0，图中端口电流、电压加上标（2），有I R I R U eq S eq -=-=)2(I I I S ==)2( 应用叠加定理，得⎪⎩⎪⎨⎧=+=-=+=I I I I I R U U U U eq oc )2()1()2()1( （1）可以看到，在戴维南等效电路中，关于ab 端的特性方程与（1）式相同。

戴维南定理和诺顿定理、最大功率传输定理分析在电路的求解过程中, 如果不要求计算全部支路的电压、电流，而只计算某支路的电压、电流或功率时，应用回路(网孔)电流法和结点电压法列写方程进行求解将十分繁琐，而采用一端口网络定理即戴维南/诺顿定理求解则较简便。

戴维南定理指出：任何线性含源一端口网络对于外部性能来说，可以用一个电压源等效代替。

其电压源的电压等于原一端口网络的开路电压Uoc，其内阻等于原一端口网络变为无源一端口网络后的入端电阻Req。

应用戴维南定理的关键是求开路电压和入端电阻。

诺顿定理指出：任何线性含源一端口网络对于外部性能来说，可以用一个电流源等效代替。

电流源的电流等于原一端口网络的短路电流Isc，其内电导Geq(或电阻Req)等于原一端口网络变为无源一端口网络后的入端电导Geq(或电阻Req)。

应用诺顿定理的关键是求短路电流Isc和入端电导Geq。

1、戴维南定理图1.14(a)中,电路结构和参数已给定,应用戴维南定理求电流I=？(图中电阻的单位为欧姆)。

分析：应用戴维南定理的关键是求出a,b两端的开路电压Uoc和入端电阻Req。

Uoc等于ab两端将负载开路后的电压；Req等于将ab左边的含源二端网络变为无源二端网络时的入端电阻。

求开路电压的等效电路如图(b)所示,方法不限。

本题用结点电压法。

入端电阻的等效电路如(c)所示；利用图(d)求出待求量。

方程式及结果如下：将负载开路,如(b)。

在(b)中求ab两端的开路电压Uoc：[(1/R1)+(1/R2)]Uoc=(Us1/R1)+IS代入数据, 解得 Uoc=32V为求入端电阻，在(b)中，将独立源置零，如(c)。

则ab两端的入端电阻：Req=4+5//20=8Ω则戴维南等效电路如图(d)。

电流I=32/(8+2)=3.2A图1.142、诺顿定理图1.15(a)中,电路结构和参数已给定,用诺顿定理求电流I=？(图中电阻的单位为欧姆)。

分析：应用诺顿定理的关键是求出a,b两端的短路电流Isc和入端电阻Req(或电导Geq),Isc等于ab两端将负载短路时的电流如图(b)所示；Req(或电导Geq)等于将ab左边的含源二端网络变为无源二端网络时的入端电阻(或电导), 其等效电路如 (c)所示；最后利用图(d)求得待求量。

戴维南定理的适用条件介绍戴维南定理，又称戴维南–洛杰斯定理，是离散数学中的一个重要定理，被广泛应用于图论、计算机科学和网络分析等领域。

该定理通过刻画了图的性质与其补图的性质之间的关系，为图论的研究提供了重要的工具。

本文将介绍戴维南定理的适用条件及其应用。

适用条件戴维南定理的适用条件主要包括以下几个方面：1. 图的顶点情况戴维南定理要求图是可递归分割的，也就是说，图的顶点集合可以被分割成两个非空且互斥的子集合。

这个分割过程可以一直进行下去，直到得到的子集合无法再被分割为止。

因此，图的顶点集合必须满足可分割性质。

2. 边的情况对于图的边集合，戴维南定理要求边的数量是有限的。

这是因为戴维南定理是基于递归的思想来证明的，而递归的停止条件需要有限性的保证。

因此，图的边数必须是有限的。

3. 图的完备性戴维南定理还要求图是完备的。

所谓完备性是指图中的每两个不同的顶点之间都存在边。

如果存在两个顶点没有边相连，则这个图是不完备的。

对于戴维南定理的应用，图的完备性是一个必要条件。

应用戴维南定理在图论、计算机科学和网络分析等领域有着广泛的应用。

以下是戴维南定理的一些应用领域：1. 图的同构性判定戴维南定理可以用于判断两个图是否同构。

如果两个图的顶点集合和边集合满足戴维南定理的适用条件，且它们的补图同构，那么这两个图是同构的。

2. 图的特征值戴维南定理可以用于研究图的特征值问题。

特征值问题是指对于一个给定的图，确定其特征矩阵的特征值和特征向量。

戴维南定理提供了一种方法来计算图的特征值和特征向量。

3. 分布式计算在分布式计算中，戴维南定理可以用于划分大规模图的顶点集合，将图的计算任务分配到不同的计算节点上进行并行计算，从而提高计算效率。

4. 社交网络分析在社交网络分析中，戴维南定理可以用于发现社交网络中的社群结构。

通过将社交网络转化为图的补图，然后应用戴维南定理进行图的划分，可以将社交网络划分为不同的社群，并对社群结构进行进一步的分析。

《电工技术》教案（2017～2018学年第1学期）适用机电一体化专业院系（部）_______机电系________班级____17机电航空___ __ 教师________ 李丽___教案首页教学设计教学内容【复习导入】【告知目的】1、戴维南定理的应用。

2、二端网络的应用。

【知识链接】一、二端网络二端网络：任何具有两个出线端的部分电路。

有源二端网络：含有电源的二端网络。

（如图a 所示）无源二端网络：不含有电源的二端网络。

（如图b 所示）如果将二端网络等效成电源，R 0，那么原来复杂电路就可化为单一回路的简单电路，我们便能方便求解未知量，所以问题的关键变成：如何计算等效电压源的电动势E 和内阻R 0？E 1bI I 3（a ）RabE rR线性 有源 二端 网络a b (a)无源二端网络二、戴维南定理戴维南定理内容：任何一个线性有源二端网络，对外电路而言，都可以用一个等效电源代替； 这个等效电源的电动势等于该网络两端点间的开路电压U ab ；等效电源的内阻等于该网络中所有电源不作用（电压源短路、电流源开路）时所得无源二端网络的输入电阻R ab 。

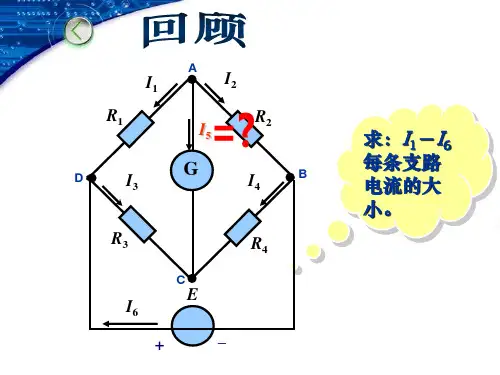
三、戴维南定理的应用1、例题：在图示电路中，已知E 1=40V ，E 2=20V ，R 1=R 2=4Ω，R 3=13 Ω，试用戴维南定理求电流I 3。

.原题图（1） 图（2）图（3） 图（4） 解：(1) 断开待求支路求等效电源的电动势 E ，如图(1)所示。

E = U 0= E 2 + I R 2 = 20+2.5 ⨯ 4= 30V(2) 求等效电源的内阻R 0，如图(1)所示。

从a 、b 两端看进去， R 1 和 R 2并联： (3) 画出等效电路求电流I 3，如图（3）所示求内阻 图(c) R 2E 1I E 2 + – R 1+ –ab+ U 0 –E 1bI I 3––ER 0+_ R 3ab I 3R 1R 2abA 5.2A 4420402121=+-=+-=R R EE I Ω=+⨯=221210R R R R R A2A 13230303=+=+=R R E I四、例题引入已知电路图如下，求出电流I 和电压U 的大小（让学生用前面所学的知识解题，巩固学生的知识点，并且可以检查学生的接受情况） 求解过程：1、利用黑板上刚才讲的例题的求解过程，分别在黑板上画出只有电压源和电流源作用的图形，进行电压和电流的求解引导学生学生发现下面的规律U sI sR 1R 2)11(/211R R I R U U ss ++=21212R R I R R R U s s ++=ss I R R R R R U I 21121+++=sU R R R U 212+='sI R R R R U 2112+=''21R R U I s +='sI R R R I 211+=''五、定理线性电路中任一条支路电流或电压等于各个独立电源单独作用时在该支路所产生的电流或电压的代数和。

戴维南定理和诺顿定理戴维南定理（Thev enin’s theorem ）是一个极其有用的定理，它是分析复杂网络响应的一个有力工具。

不管网络如何复杂，只要网络是线性的，戴维南定理提供了同一形式的等值电路。

先了解一下二端网络/也叫一端口网络的概念。

（一个网络具有两个引出端与外电路相联，不管其内部结构多么复杂，这样的网络叫一端口网络）。

含源单口（一端口)网络──内部含有电源的单口网络。

单口网络一般只分析端口特性.这样一来，在分析单口网络时,除了两个连接端钮外，网络的其余部分就可以置于一个黑盒子之中.含源单口网络的电路符号：图中N ──网络 方框──黑盒子U单口松驰网络──含源单口网络中的全部独立电源置零，受控电源保留，(动态元件为零状态），这样的网络称为单口松驰网络。

电路符号：一、戴维南定理(一）定理:一含源线性单口一端网络N ，对外电路来说,可以用一个电压源和电阻的串联组合来等效置换，此电压源的电压等于端口的开路电压，电阻等于该单口网络对应的单口松驰网络的输入电阻.(电阻等于该单口网络的全部独立电源置零后的输入电阻).上述电压源和电阻串联组成的电压源模型,称为戴维南等效电路.该电阻称为戴维南等效电阻.U任意负载任意负载U oc =U s求戴维南等效电路,对负载性质没有限定。

用戴维南等效电路置换单口网络后，对外电路的求解没有任何影响，即外电路中的电流和电压仍然等于置换前的值。

(二）戴维南定理的证明：1. 设一含源二端网络N 与任意负载相接，负载端电压为U ，端电流为I 。

2。

任意负载用电流源替代，取电流源的电流为I I S 。

方向与I 相同.替代后，整个电路中的电流、电压保持不变. 下面用叠加定理分析端电压U 与端电流I 。

3。

设网络N 内的独立电源一起激励，受控源保留,电流源I S 置零，即ab 端开路.这时端口电压、电流加上标（1），有4. I S 单独激励,网络N 内的独立电源均置零，受控电源保留，这时，含源二端网络N 转化成单口松驰网络N 0,图中端口电流、电压加上标（2），SU (1)=U ocI (1)=0(2)S有I R I R U eq S eq -=-=)2( I I I S ==)2(应用叠加定理，得⎪⎩⎪⎨⎧=+=-=+=I I I I I R U U U U eq oc )2()1()2()1(（1） 可以看到，在戴维南等效电路中，关于ab 端的特性方程与（1）式相同。

戴维南定理的适用范围
戴维南定理：一个连续函数的导数可以使用积分来求解。

戴维南定理是求解一个连续函数的导数的重要定理，它由英国数学家阿尔弗雷德·戴维南在1830年首次提出。

它的定义是：如果一个函数在一个闭区间上连续，那么它的导数在这个闭区间上也是连续的，这种函数可以用积分来求解它的导数。

简单来说，戴维南定理表明，如果一个函数在一个闭区间上连续，那么它的导数也必须在该闭区间上连续，并且可以通过积分来求解它的导数。

这是一个非常有用的定理，因为它可以帮助我们解决一些关于导数的问题。

戴维南定理的适用范围可以用一句话来总结：它可以用来求解一个在某个区间上连续的函数的导数。

它给我们提供了一个有用的计算机技术，可以帮助我们计算函数的导数。

总之，戴维南定理提供了一种有效的方法来解决一些关于导数的问题，它的适用范围是一个在某个区间上连续的函数的导数，并且可以通过积分来求解它的导数。