2019版同步优化探究文数(北师大版)练习：第七章 第一节 空间几何体的结构特征及三视图与直观图 含解析

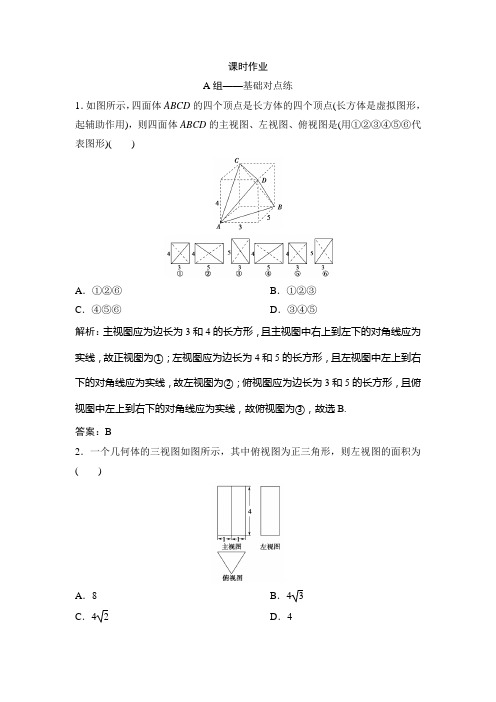
课时作业A组——基础对点练1．如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的主视图、左视图、俯视图是(用①②③④⑤⑥代表图形)()A．①②⑥B．①②③C．④⑤⑥D．③④⑤解析：主视图应为边长为3和4的长方形，且主视图中右上到左下的对角线应为实线，故正视图为①；左视图应为边长为4和5的长方形，且左视图中左上到右下的对角线应为实线，故左视图为②；俯视图应为边长为3和5的长方形，且俯视图中左上到右下的对角线应为实线，故俯视图为③，故选B.答案：B2．一个几何体的三视图如图所示，其中俯视图为正三角形，则左视图的面积为()A．8B．4 3C．4 2 D．4解析：由三视图可知，该几何体是一个正三棱柱，高为4，底面是一个边长为2的正三角形．因此，左视图是一个长为4，宽为3的矩形，其面积S＝3×4＝4 3.答案：B3．某几何体的三视图如图所示，则该几何体中最长的棱长为()A．3 3 B．2 6C.21 D．2 5解析：由三视图得，该几何体是四棱锥P-ABCD，如图所示，ABCD为矩形，AB＝2，BC＝3，平面P AD⊥平面ABCD，过点P作PE⊥AD，则PE＝4，DE＝2，所以CE＝22，所以最长的棱PC＝PE2＋CE2＝26，故选B.答案：B4．某空间几何体的三视图如图所示，则该几何体的表面积为()A．12＋4 2 B．18＋8 2C．28 D．20＋8 2解析：由三视图可知该几何体是底面为等腰直角三角形的直三棱柱，如图．则该几何体的表面积为S＝2×12×2×2＋4×2×2＋22×4＝20＋82，故选D.答案：D5．已知某几何体的三视图如图所示，则该几何体的表面积是( )A ．(25＋35)πB ．(25＋317)πC ．(29＋35)πD ．(29＋317)π解析：由三视图可知该几何体的直观图如图所示，所以该几何体的表面积为π＋π×(1＋2)×17＋2×π×2×4＋4π×222＝π＋317π＋16π＋8π＝(25＋317)π，故选B. 答案：B6．某几何体的三视图如图所示，则该几何体的体积为( )A ． 16＋8πB ．8＋8πC ．16＋16πD ．8＋16π解析：由三视图复原的几何体是一个长方体与半个圆柱的组合体，如图．其中长方体的长、宽、高分别是4,2,2，半个圆柱的底面半径为2，母线长为4.∴长方体的体积V 1＝4×2×2＝16， 半个圆柱的体积V 2＝12×22×π×4＝8π. ∴这个几何体的体积是16＋8π. 答案：A7．一个半径为2的球体经过切割之后所得几何体的三视图如图所示，则该几何体的表面积为( )A ．16πB ．12πC ．14πD ．17π解析：根据三视图可知几何体是一个球体切去四分之一，则该几何体的表面是四分之三球面和两个截面(半圆)． 由题意知球的半径是2，∴该几何体的表面积S ＝34×4π×22＋π×22＝16π. 答案：A8．球面上有A ，B ，C 三点，球心O 到平面ABC 的距离是球半径的13，且AB ＝22，AC ⊥BC ，则球O 的表面积是( ) A ．81π B ．9π C.81π4D.9π4解析：由题意可知，AB 为△ABC 的外接圆的直径，设球O 的半径为R ，则R 2＝(R 3)2＋(2)2，可得R ＝32，则球的表面积S ＝4πR 2＝9π.故选B.答案：B9．某几何体的三视图如图所示，则该几何体的体积为 ．解析：将三视图还原成直观图，得到如图所示几何体，设BC 的中点为G ，连接AG ，DG ，△ABC 是一个边长为2的等边三角形，其高AG ＝ 3.该几何体可以看成一个三棱锥与一个四棱锥组合而成．∴该几何体的体积V ＝V三棱锥D -ABG ＋V 四棱锥A -DECG ＝13×S △ABG ×DG＋13×S 四边形DECG ×AG ＝13×12×1×3×2＋13×2×1×3＝ 3. 答案： 310．某空间几何体的三视图如图所示，则该几何体的体积为 ．解析：由题意得到几何体的直观图如图，即从四棱锥P ABCD 中挖去了一个半圆锥．其体积V ＝13×2×2×2－12×13×π×12×2＝8－π3.答案：8－π3B 组——能力提升练1．若三棱锥S -ABC 的底面是以AB 为斜边的等腰直角三角形，AB ＝SA ＝SB ＝SC ＝2，则该三棱锥的外接球的表面积为( ) A.16π3 B.8π3 C.43π3D.4π3解析：在等腰直角三角形ABC 中，AB 是斜边且AB ＝2，取AB 的中点D ，连接CD ，SD .∴CD ＝AD ＝BD ＝1.又SA ＝SB ＝SC ＝2，∴SD ⊥AB ，且SD ＝3，在△SCD 中，SD 2＋CD 2＝SC 2，∴SD ⊥CD ，∴SD ⊥平面ABC .∴三棱锥S -ABC 的外接球球心在SD 上，记为O ，设球半径为R ，连接OA ，则SO ＝OA ＝R ，∴在Rt △AOD 中，AD ＝1，OD ＝3－R ，AO ＝R ，∴12＋(3－R )2＝R 2⇒R ＝233，∴三棱锥S -ABC 的外接球的表面积S ＝4πR 2＝4π×(233)2＝16π3.故选A. 答案：A2．一个几何体的三视图如图所示，则该几何体的体积为( )A.163B.203C.152D.132解析：该几何体可视为正方体截去两个三棱锥所得，如图所示，所以其体积为23－13×12×2×2×2－13×12×1×1×1＝132.故选D. 答案：D3．高为4的直三棱柱被削去一部分后得到一个几何体，它的直观图和三视图中的左视图、俯视图如图所示，则该几何体的体积是原直三棱柱的体积的( )A.34B.14C.12D.38解析：由左视图、俯视图知该几何体是高为2、底面积为12×2×(2＋4)＝6的四棱锥，其体积为4.易知直三棱柱的体积为8，则该几何体的体积是原直三棱柱的体积的48＝12，故选C. 答案：C4．如图，某三棱锥的主视图、左视图和俯视图分别是直角三角形、等腰三角形和等边三角形．若该三棱锥的顶点都在同一个球面上，则该球的表面积为( )A ．27πB ．48πC ．64πD ．81π解析：由三视图可知该几何体为三棱锥，该棱锥的高VA ＝4，棱锥底面ABC 是边长为6的等边三角形，作出直观图如图所示．因为△ABC 是边长为6的等边三角形，所以外接球的球心D 在底面ABC 上的投影为△ABC 的中心O ，过D 作DE ⊥VA 于E ，则E 为VA 的中点，连接OD ，OA ，DA ，则DE ＝OA ＝23×33＝23，AE ＝12VA ＝2，DA 为外接球的半径，所以DA ＝DE 2＋AE 2＝4，所以外接球的表面积S ＝4πr 2＝64π.故选C.答案：C5．(2018·天津测试)若一个几何体的表面积和体积相同，则称这个几何体为“同积几何体”．已知某几何体为“同积几何体”，其三视图如图所示，则a ＝( )A.14＋223B.8＋223C.12＋223D ．8＋2 2解析：根据几何体的三视图可知该几何体是一个四棱柱，如图所示，可得其体积为12(a ＋2a )·a ·a ＝32a 3，其表面积为12·(2a＋a )·a ·2＋a 2＋a 2＋2a ·a ＋2a ·a ＝7a 2＋2a 2，所以7a 2＋2a 2＝32a 3，解得a ＝14＋223，故选A. 答案：A6．(2018·郑州质检)如图所示是一个几何体的三视图，则这个几何体外接球的表面积为()A．8π B．16πC．32π D．64π解析：还原三视图可知该几何体为一个四棱锥，将该四棱锥补成一个长、宽、高分别为22，22，4的长方体，则该长方体外接球的半径r＝(22)2＋(22)2＋422＝22，则所求外接球的表面积为4πr2＝32π.答案：C7．(2018·南昌模拟)某四棱锥的三视图如图所示，则该四棱锥最长的一条侧棱的长度是．解析：由题意可知该几何体是一个底面为直角梯形的四棱锥，梯形的两底边长分别为4,2，高为3，棱锥的高为2，所以最长侧棱的长度为22＋32＋42＝29.答案：298．在三棱锥A BCD中，侧棱AB，AC，AD两两垂直，△ABC，△ACD，△ADB的面积分别为22，32，62，则该三棱锥外接球的表面积为．解析：设相互垂直的三条侧棱AB，AC，AD分别为a，b，c，则12ab＝22，12bc＝32，12ac＝62，解得a＝2，b＝1，c＝ 3.所以三棱锥A BCD的外接球的直径2R＝a2＋b2＋c2＝6，则其外接球的表面积S＝4πR2＝6π.答案：6π9．一个直三棱柱被削去一部分后的几何体ABCDE及其左视图、俯视图如图所示，其中左视图是直角梯形，俯视图是等腰直角三角形．设M 是BD 的中点，点N 在棱DC 上，且MN ⊥平面BDE ，则CN ＝ .解析：由题意可得，DC ⊥平面ABC ，所以DC ⊥CB .若MN ⊥平面BDE ，则MN ⊥BD .又因为∠MDN ＝∠CDB ，所以△DMN ∽△DCB ，所以DN DB ＝DM DC ，故DN 26＝64，解得DN ＝3，所以CN ＝CD －DN ＝1. 答案：1。

课时作业 A 组——基础对点练1、(2018·合肥市质检)已知一个圆锥底面半径为1，母线长为3，则该圆锥内切球的表面积为( ) A 、π B.3π2 C 、2πD 、3π解析：依题意，作出圆锥与球的轴截面，如图所示，设球的半径为r ，易知轴截面三角形边AB 上的高为22，因此22－r 3＝r1，解得r ＝22，所以圆锥内切球的表面积为4π×(22)2＝2π，故选C. 答案：C2、平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为( ) A.6π B 、43π C 、46πD 、63π解析：设球的半径为R ，由球的截面性质得R ＝(2)2＋12＝3，所以球的体积V ＝43πR 3＝43π. 答案：B3、已知一个几何体的三视图如图所示，则该几何体的体积为( )A.323B.163C.83D.43解析：该几何体由一个三棱锥和一个三棱柱组合而成，直观图如图所示，V ＝V 柱＋V 锥＝12×(1＋1)×1×2＋13×12×(1＋1)×1×2＝83，故选C. 答案：C4、如图，网格纸上小正方形的边长为1，粗线(实线和虚线)表示的是某几何体的三视图，则该几何体外接球的表面积为( )A 、24πB 、29πC 、48πD 、58π解析：如图，在3×2×4的长方体中构造符合题意的几何体(三棱锥A BCD )，其外接球即为长方体的外接球，表面积为4πR 2＝π(32＋22＋42)＝29π.答案：B5、(2018·合肥市质检)如图，网格纸上小正方形的边长为1，实线画出的是某多面体的三视图，则该多面体的体积为( )A 、3B 、3 2C 、9D 、9 2解析：由题中的三视图，可得该几何体是一个以俯视图中的梯形为底面的四棱锥，其底面面积S ＝12×(2＋4)×1＝3，高h ＝3，故其体积V ＝13Sh ＝3，故选A. 答案：A6、若三棱锥P ABC 的最长的棱P A ＝2，且各面均为直角三角形，则此三棱锥的外接球的体积是 、解析：如图，根据题意，可把该三棱锥补成长方体，则该三棱锥的外接球即该长方体的外接球，易得外接球的半径R ＝12P A ＝1，所以该三棱锥的外接球的体积V＝43×π×13＝43π.答案：43π7、已知矩形ABCD 的顶点都在半径为2的球O 的球面上，且AB ＝3，BC ＝3，过点D 作DE 垂直于平面ABCD ，交球O 于E ，则棱锥E ABCD 的体积为 、解析：如图所示，BE 过球心O ，∴DE ＝42－32－(3)2＝2，∴V E －ABCD ＝13×3×3×2＝2 3. 答案：2 38、已知H 是球O 的直径AB 上一点，AH ∶HB ＝1∶2，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为 、解析：如图，设截面小圆的半径为r ，球的半径为R ，因为AH ∶HB ＝1∶2，所以OH ＝13R .由勾股定理，有R 2＝r 2＋OH 2，又由题意得πr 2＝π，则r ＝1，故R 2＝1＋(13R )2，即R 2＝98.由球的表面积公式，得S ＝4πR 2＝9π2.答案：9π29、如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置、(1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝54，OD ′＝22，求五棱锥D ′-ABCFE 的体积、 解析：(1)证明：由已知得AC ⊥BD ，AD ＝CD . 又由AE ＝CF 得AE AD ＝CFCD ，故AC ∥EF .由此得EF ⊥HD ，EF ⊥HD ′，所以AC ⊥HD ′.(2)由EF∥AC得OHDO＝AEAD＝14.由AB＝5，AC＝6得DO＝BO＝AB2－AO2＝4.所以OH＝1，D′H＝DH＝3.于是OD′2＋OH2＝(22)2＋12＝9＝D′H2，故OD′⊥OH.由(1)知，AC⊥HD′，又AC⊥BD，BD∩HD′＝H，所以AC⊥平面BHD′，于是AC⊥OD′.又由OD′⊥OH，AC∩OH＝O，所以OD′⊥平面ABC.又由EFAC ＝DHDO得EF＝92.五边形ABCFE的面积S＝12×6×8－12×92×3＝694.所以五棱锥D′-ABCFE的体积V＝13×694×22＝2322.10.(2018·莆田质检)如图，在四棱锥S ABCD中，四边形ABCD为矩形，E为SA的中点，SA＝SB＝2，AB＝23，BC＝3.(1)证明：SC∥平面BDE；(2)若BC⊥SB，求三棱锥C BDE的体积、解析：(1)证明：连接AC，设AC∩BD＝O，∵四边形ABCD为矩形，则O为AC的中点、在△ASC中，E为AS的中点，∴SC∥OE，又OE平面BDE，SC平面BDE，∴SC∥平面BDE.(2)∵BC ⊥AB ，BC ⊥SB ，AB ∩SB ＝B ，∴BC ⊥平面SAB ，又BC ∥AD ，∴AD ⊥平面SAB . ∵SC ∥平面BDE ，∴点C 与点S 到平面BDE 的距离相等， ∴V CBDE ＝V SBDE ＝V D SBE ，在△ABS 中，SA ＝SB ＝2，AB ＝23， ∴S △ABS ＝12×23×1＝ 3.又∵E 为AS 的中点，∴S △BES ＝12S △ABS ＝32. 又点D 到平面BES 的距离为AD ， ∴V D BES＝13S △BES ·AD ＝13×32×3＝32， ∴V CBDE ＝32，即三棱锥CBDE 的体积为32. B 组——能力提升练1、(2018·湖北七市联考)一个几何体的三视图如图所示，该几何体外接球的表面积为( )A 、36π B.1123π C 、32πD 、28π解析：根据三视图，可知该几何体是一个四棱锥，其底面是一个边长为4的正方形，高是2 3.将该四棱锥补形成一个三棱柱，如图所示，则其底面是边长为4的正三角形，高是4，该三棱柱的外接球即为原四棱锥的外接球、∵三棱柱的底面是边长为4的正三角形，∴底面三角形的中心到该三角形三个顶点的距离为23×23＝433，∴外接球的半径R ＝ ⎝ ⎛⎭⎪⎫4332＋22＝283，外接球的表面积S ＝4πR 2＝4π×283＝112π3，故选B. 答案：B2、(2018·广州模拟)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马；将四个面都为直角三角形的三棱锥称为鳖臑、若三棱锥P ABC 为鳖臑，P A ⊥平面ABC ，P A ＝AB ＝2，AC ＝4，三棱锥P ABC 的四个顶点都在球O 的球面上，则球O 的表面积为( ) A 、8π B 、12π C 、20πD 、24π解析：如图，因为四个面都是直角三角形，所以PC 的中点到每一个顶点的距离都相等，即PC 的中点为球心O ，易得2R ＝PC ＝20，所以R ＝202，球O 的表面积为 4πR 2＝20π，选C.答案：C3、在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球、若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( ) A 、4π B.9π2 C 、6πD.32π3解析：由题意可得若V 最大，则球与直三棱柱的部分面相切，若与三个侧面都相切，可求得球的半径为2，球的直径为4，超过直三棱柱的高，所以这个球放不进去，则球可与上下底面相切，此时球的半径R ＝32，该球的体积最大，V max ＝43πR 3＝4π3×278＝9π2. 答案：B 4、四棱锥SABCD 的所有顶点都在同一个球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥体积取得最大值时，其表面积等于8＋83，则球O 的体积等于( ) A.32π3 B.322π3 C 、16πD.162π3解析：依题意，设球O 的半径为R ，四棱锥SABCD 的底面边长为a 、高为h ，则有h ≤R ，即h 的最大值是R ，又AC ＝2R ，则四棱锥S ABCD 的体积V SABCD＝13×2R 2h ≤2R 33.因此，当四棱锥SABCD 的体积最大，即h ＝R 时，其表面积等于(2R )2＋4×12×2R × (2R2)2＋R 2＝8＋83，解得R ＝2，因此球O 的体积等于4πR 33＝32π3，选A. 答案：A5、(2017·河北质量监测)多面体的三视图如图所示，则该多面体的体积为 cm 3.解析：由三视图可知该几何体是一个三棱锥，如图所示，在三棱锥D ABC 中，底面ABC 是等腰三角形，设底边AB 的中点为E ，则底边AB 及底边上的高CE 均为4，侧棱AD ⊥平面ABC ，且AD ＝4，所以三棱锥D ABC 的体积V ＝13S △ABC ·AD ＝13×12×4×4×4＝323(cm 3)、 答案：3236、已知正四棱锥OABCD 的体积为322，底面边长为3，则以O 为球心，OA为半径的球的表面积为 、解析：过O 作底面ABCD 的垂线段OE (图略)，则E 为正方形ABCD 的中心、由题意可知13×(3)2×OE ＝322，所以OE ＝322，故球的半径R ＝OA ＝OE 2＋EA 2＝6，则球的表面积S ＝4πR 2＝24π. 答案：24π7、如图，已知正三棱锥P -ABC 的侧面是直角三角形，P A ＝6.顶点P 在平面ABC 内的正投影为点D ，D 在平面P AB 内的正投影为点E ，连接PE 并延长交AB 于点G .(1)证明：G是AB的中点；(2)在图中作出点E在平面P AC内的正投影F(说明作法及理由)，并求四面体PDEF的体积、解析：(1)证明：因为P在平面ABC内的正投影为D，所以AB⊥PD.因为D在平面P AB内的正投影为E，所以AB⊥DE.因为PD∩DE＝D，所以AB⊥平面PED，故AB⊥PG.又由已知，可得P A＝PB，所以G是AB的中点、(2)在平面P AB内，过点E作PB的平行线交P A于点F，F即为E在平面P AC内的正投影、理由如下：由已知可得PB⊥P A，PB⊥PC，又EF∥PB，所以EF⊥P A，EF⊥PC.因此EF⊥平面P AC，即点F为E在平面P AC内的正投影、连接CG，因为P在平面ABC内的正投影为D，所以D是正三角形ABC的中心、由(1)知，G是AB的中点，所以D在CG上，故CD＝23CG.由题设可得PC⊥平面P AB，DE⊥平面P AB，所以DE∥PC，因此PE＝23PG，DE＝13PC.由已知，正三棱锥的侧面是直角三角形且P A＝6，可得DE＝2，PE＝2 2.在等腰直角三角形EFP中，可得EF＝PF＝2，所以四面体PDEF 的体积V ＝13×12×2×2×2＝43.8、(2018·西安调研)如图所示，平行四边形ABCD 中，∠DAB ＝60°，AB ＝2，AD ＝4.将△CBD 沿BD 折起到△EBD 的位置，使平面EBD ⊥平面ABD .(1)求证：AB ⊥DE ；(2)求三棱锥E ABD 的侧面积和体积、解析：(1)证明：在△ABD 中，∵AB ＝2，AD ＝4，∠DAB ＝60°，∴BD ＝AB 2＋AD 2－2AB ·AD cos ∠DAB ＝2 3.∴AB 2＋BD 2＝AD 2，∴AB ⊥BD .又平面EBD ⊥平面ABD ，平面EBD ∩平面ABD ＝BD ，AB 平面ABD ， ∴AB ⊥平面EBD .又DE平面EBD ，∴AB ⊥DE .(2)由(1)知AB ⊥BD .∵CD ∥AB ，∴CD ⊥BD ，从而DE ⊥BD .在Rt △DBE 中，∵DB ＝23，DE ＝DC ＝AB ＝2，∴S △EDB ＝12DB ·DE ＝2 3.∵AB ⊥平面EBD ，BE 平面EBD ，∴AB ⊥BE . ∵BE ＝BC ＝AD ＝4，∴S △EAB ＝12AB ·BE ＝4.∵DE ⊥BD ，平面EBD ⊥平面ABD ，∴ED ⊥平面ABD ，而AD 平面ABD ，∴ED ⊥AD ，∴S △EAD ＝12AD ·DE ＝4.综上，三棱锥E ABD 的侧面积S ＝S △EDB ＋S △EAB ＋S △EAD ＝8＋2 3.∵DE⊥平面ABD，且S△ABD＝S△EBD＝23，DE＝2，∴V E ABD＝13S△ABD·DE＝13×23×2＝433.。

陕西北师版数学文复习方略课时提升作业第七章第一节空间几何体的结构特征及三视图和直观图温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

课时提升作业(四十)一、选择题1.以下四个命题:①正棱锥的所有侧棱相等;②直棱柱的侧面都是全等的矩形;③圆柱的母线垂直于底面;④用经过旋转轴的平面截圆锥,所得的截面一定是全等的等腰三角形.其中,真命题的个数为()(A)4(B)3(C)2(D)12.下列几何体各自的三视图中,有且仅有两个视图相同的是()(A)①②(B)①③(C)①④(D)②④3.(2022安康模拟)一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是()4.如图,△ABC为正三角形,AA′∥BB′∥CC′,CC′⊥平面ABC且3AA′=BB′=CC′=AB,则多面体ABC-A′B′C′的主视图是()5.(2022·铜川模拟)一个水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为()(A)+(B)2+(C)+(D)+6.(能力挑战题)一个正方体截去两个角后所得几何体的主视图、左视图如图所示,则其俯视图为()7.(2022·西安模拟)一只蚂蚁从正方体ABCD-A1B1C1D1的顶点A处出发,经正方体的表面,按最短路线爬行到达顶点C1位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的主视图是()(A)①②(B)①③(C)②④(D)③④二、填空题8.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为某轴,则由斜二测画法画出的直观图A′B′C′D′的面积为.9.(2022·德州模拟)一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,左视图是一个矩形,则这个矩形的面积是.10.(2022·宝鸡模拟)一个三棱锥的主视图和左视图及其尺寸如图所示,则该三棱锥的俯视图的面积为.三、解答题11.(能力挑战题)某几何体的一条棱长为,在该几何体的主视图中,这条棱的投影是长为的线段,在该几何体的左视图与俯视图中,这条棱的投影分别是长为a和b的线段,求a+b的最大值.答案解析1.【解析】选B.由正棱锥的定义可知所有侧棱相等,故①正确;由于直棱柱的底面的各边不一定相等,故侧面矩形不一定全等,因此②不正确;由圆柱母线的定义可知③正确;结合圆锥轴截面的作法可知④正确.综上,正确的命题有3个.2.【解析】选D.在各自的三视图中,①正方体的三个视图都相同;②圆锥的两个视图相同;③三棱台的三个视图都不同;④正四棱锥的两个视图相同,故选D.【变式备选】正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1如图所示,以四边形ABB1A1为水平面,四边形BCC1B1的前面为正前方画出的三视图正确的是()【解析】选A.矩形图为矩形,左侧为△ABC,BCC1B1的前面为正前方,故主视所以左视图为三角形.俯视图为两个有公共边的矩形,公共边为CC1在面ABB1A1内的投影,故选A.3.【解析】选C.当俯视图为A,B时表示底面为等腰直角三角形,且过直角顶点的棱与底面垂直的三棱锥.当俯视图为D时,表示底面为正方形,且有一条侧棱与底面垂直的四棱锥.故选C.【方法技巧】由直观图画三视图的技巧(1)可以想象将一几何体放在自己面前,然后从正前方,左侧及上面观察该几何体,进而得到主视图、左视图和俯视图.(2)在画三视图时,要注意看得见的轮廓线画成实线,看不见的轮廓线画成虚线.4.【解析】选D.由AA′∥BB′∥CC′及CC′⊥平面ABC,知AA′⊥平面ABC,BB′⊥平面ABC.又CC′=BB′=3AA′,且△ABC为正三角形,故主视图应为D中的图形.5.【解析】选B.如图将直观图ABCD还原后为直角梯形A′BCD′,其中A′B=2AB=2,BC=1+,A′D′=AD=1,∴S=某(1+1+)某2=2+.6.【解析】选C.依题意可知该几何体的直观图如图所示,故其俯视图应为C.。

课时作业A 组——基础对点练1．平面α的一个法向量为v 1＝(1,2,1)，平面β的一个法向量为v 2＝(－2，－4，－2)，则平面α与平面β( )A ．平行 B ．垂直C ．相交D ．不确定解析：由v 1∥v 2故可判断α∥β.答案：A2．若＝λ＋μ，则直线AB 与平面CDE 的位置关系是( )AB → CD → CE→ A ．相交 B ．平行C ．在平面内D ．平行或在平面内答案：D3．已知平面α内有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则下列点P 中，在平面α内的是( )A ．P (2,3,3) B ．P (－2,0,1)C ．P (－4,4,0) D ．P (3，－3,4)答案：A4．设平面α的法向量为(1,2，－2)，平面β的法向量为(－2，－4，k )，若α∥β，则k ＝( )A ．2 B ．－4C ．4D ．－2解析：∵α∥β，∴＝＝，∴k ＝4，故选C.1－22－4－2k 答案：C5.在正方体ABCD ­A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 、AC 的中点，则MN 与平面BB 1C 1C 的位置关系是( )A ．相交 B ．平行C ．垂直D．不能确定答案：B6.(2018·西安月考)如图，F 是正方体ABCD ­A 1B 1C 1D 1的棱CD 的中点．E 是BB 1上一点，若D 1F ⊥DE ，则有( )A ．B 1E ＝EBB ．B 1E ＝2EBC ．B 1E ＝EBD ．E 与B 重合12答案：A7.如图所示，在平行六面体ABCD ­A 1B 1C 1D 1中，点M ，P ，Q 分别为棱AB ，CD ，BC 的中点，若平行六面体的各棱长均相等，则：①A 1M ∥D 1P ；②A 1M ∥B 1Q ；③A 1M ∥平面DCC 1D 1；④A 1M ∥平面D 1PQB 1.以上说法正确的个数为( )A ．1 B ．2C ．3 D ．4答案：C8．若＝λ＋μ(λ，μ∈R )，则直线AB 与平面CDE 的位置关系是 AB → CD → CE→ ．答案：AB ∥平面CDE 或AB 平面CDE9．(2018·武汉调研)已知平面α内的三点A (0,0,1)，B (0，1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是 ．答案：α∥β10．(2018·西安调研)已知＝(1,5，－2)，＝(3,1，z )，若AB → BC→ ⊥，＝(x －1，y ，－3)，且BP ⊥平面ABC ，则实数x ＋y ＝.AB→ BC → BP →答案：25711.如图所示，在空间四边形ABCD 中，AB ＝BC ，CD ＝DA ，E ，F ，G 分别是CD ，DA 和AC 的中点，则平面BEF 与平面BDG 的位置关系是 ．解析：由AB ＝BC ，G 是AC 中点得BG ⊥AC ，由CD ＝DA ，G 是AC 中点得DG ⊥AC ，∴AC ⊥平面GBD ，又EF ∥AC ，∴EF ⊥平面GBD ，∴平面BEF ⊥平面BDG .答案：垂直12.如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝PD .证明：平面PQC ⊥12平面DCQ .证明：如图，以D 为坐标原点，线段DA 的长为单位长，射线DA ，DP ，DC 分别为x 轴，y 轴，z 轴的正半轴，建立空间直角坐标系D ­xyz.依题意有Q (1,1,0)，C (0,0,1)，P (0,2,0)，则＝(1,1,0)，＝(0,0,1)，＝(1，－1,0)．DQ → DC → PQ→ ∴·＝0，·＝0.PQ → DQ → PQ→ DC → 即PQ ⊥DQ ，PQ ⊥DC ，又DQ ∩DC ＝D ，∴PQ ⊥平面DCQ ，又PQ 平面PQC ，∴平面PQC ⊥平面DCQ.13．在底面是菱形的四棱锥P ­ABCD 中，∠ABC ＝60°，PA ＝AC ＝a ，PB ＝PD ＝a ，F 为PC 的中点，点E 在PD 上，且＝2，求证：2PEED BF ∥平面AEC .证明：∵＝＋＝＋(＋)＝＋＋BF → BC → 12CP → AD → 12CD → DP → AD → 12CD → 32DE→ ＝＋(－)＋(－)＝－，AD → 12AD → AC → 32AE → AD → 32AE → 12AC →∴、、共面．BF→ AE → AC → 又BF 平面AEC ，从而BF ∥平面AEC .14．已知三棱锥P ­ABC ，D 、E 、F 分别为棱PA 、PB 、PC 的中点，求证平面DEF ∥平面ABC .证明：如图．设＝a ，＝b ，＝c ，则由条件知，＝2a ，＝2b ，＝2c ，PD → PE → PF → PA → PB → PC→ 设平面DEF 的法向量为n ，则n ·＝0，n ·＝0，DE → DF→ ∴n ·(b －a )＝0，n ·(c －a )＝0，∴n ·＝n ·(－)＝n ·(2b －2a )＝0，n ·＝n ·(－)＝n ·(2c －2a )AB → PB → PA → AC → PC→ PA → ＝0，∴n ⊥，n ⊥，AB → AC→ ∴n 是平面ABC 的法向量，∴平面DEF ∥平面ABC .B 组——能力提升练1.如图，正方形ABCD 与矩形ACEF 所在平面互相垂直，AB ＝，AF ＝1，M 在EF 上，且AM ∥平面BDE .则M 点的坐标为( )2A ．(1,1,1)B ．(，，1)2323C ．(，，1) D ．(，，1)22222424答案：C2．(2018·合肥调研)如图所示，在正方体ABCD ­A 1B 1C 1D 1中，棱长为a ，M ，N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝，2a3则MN 与平面BB 1C 1C 的位置关系是( )A ．相交 B ．平行C ．垂直 D ．不能确定答案：B3.如图，正方体ABCD ­A 1B 1C 1D 1的棱长为1，E ，F 分别是棱BC ，DD 1上的点，如果B 1E ⊥平面ABF ，则CE 与DF 的和的值为 ．答案：14．已知点P 是平行四边形ABCD 所在平面外一点，如果＝(2，－1，－4)，AB→ ＝(4,2,0)，＝(－1,2，－1)．对于结论：①AP ⊥AB ；②AP ⊥AD ；③是AD → AP → AP → 平面ABCD 的法向量；④∥.其中正确的是．AP→ BD → 解析：·＝2×(－1)＋(－1)×2＋(－4)×(－1)＝－2－2＋4＝0，则⊥.AB → AP → AB→ AP → ·＝4×(－1)＋2×2＋0＝0，则⊥，AP → AD → AP→ AD → ∵⊥，⊥，∩＝A ，AP→ AB → AP → AD →AB → AD → ∴⊥平面ABCD ，故是平面ABCD 的一个法向量．AP → AP→答案：①②③5.(2018·郑州调研)如图所示，四棱锥P ­ABCD 的底面是边长为1的正方形，PA ⊥CD ，PA ＝1，PD ＝，E 为PD 上2一点，PE ＝2ED .(1)求证：PA ⊥平面ABCD ；(2)在侧棱PC 上是否存在一点F ，使得BF ∥平面AEC ？若存在，指出F 点的位置，并证明；若不存在，说明理由．解析：(1)证明：∵PA ＝AD ＝1，PD ＝，2∴PA 2＋AD 2＝PD 2，即PA ⊥AD .又PA ⊥CD ，AD ∩CD ＝D ，∴PA ⊥平面ABCD .(2)以A 为原点，AB ，AD ，AP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系．则A (0,0,0)，B (1,0,0)，C (1,1,0)，P (0,0,1)，E (0，，)，2313＝(1,1,0)，AC→ ＝(0，，)．设平面AEC 的法向量为n ＝(x ，y ，z )，AE → 2313则Error!即Error!令y ＝1，则n ＝(－1,1，－2)．假设侧棱PC 上存在一点F ，且＝λ(0≤λ≤1)，CF → CP→ 使得BF ∥平面AEC ，则·n ＝0.BF→ 又∵＝＋＝(0,1,0)＋(－λ，－λ，λ)＝(－λ，1－λ，λ)，BF→ BC → CF → ∴·n ＝λ＋1－λ－2λ＝0，∴λ＝，BF→ 12∴存在点F ，使得BF ∥平面AEC ，且F 为PC 的中点．6．如图，在棱长为2的正方体ABCD ­A1B1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0＜λ＜2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ ；(2)是否存在λ，使平面EFPQ ⊥平面PQMN ？若存在，求出实数λ的值；若不存在，说明理由．解析：(1)证明：以D 为坐标原点，建立如图所示的空间直角坐标系．由已知得B (2,2,0)，C 1(0,2,2)，E (2,1,0)，F (1，0,0)，P (0,0，λ)，M (2,1,2)，N (1,0,2)，＝(－2,0,2)，＝(－1,0，λ)，＝(1,1,0)，＝(－1，－1,0)，BC 1→ FP → FE → MN→ ＝(－1,0，λ－2)．当λ＝1时，＝(－1,0,1)，NP → FP→ 因为＝(－2,0,2)，BC1→所以＝2，BC 1→ FP → 即BC 1∥FP .而FP 平面EFPQ ，且BC 1平面EFPQ ，故直线BC 1∥平面EFPQ .(2)设平面EFPQ 的一个法向量为n ＝(x ，y ，z )，则由Error!可得Error!于是可取n ＝(λ，－λ，1)．同理可得平面PQMN 的一个法向量为m ＝(λ－2，2－λ，1)．则m ·n ＝(λ－2,2－λ，1)·(λ，－λ，1)＝0，即λ(λ－2)－λ(2－λ)＋1＝0，解得λ＝1±.222故存在λ＝1±，使平面EFPQ⊥平面PQMN.2。

课时作业A 组——基础对点练1．(2018·合肥市质检)已知一个圆锥底面半径为1，母线长为3，则该圆锥内切球的表面积为( )A ．π B.3π2C ．2πD ．3π解析：依题意，作出圆锥与球的轴截面，如图所示，设球的半径为r ，易知轴截面三角形边AB 上的高为2，因此＝，解得r ＝，所以圆锥222－r3r122内切球的表面积为4π×()2＝2π，故选C.22答案：C2．平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为，则此球的体积2为( )A.π B ．4π63C ．4πD ．6π63解析：设球的半径为R ，由球的截面性质得R ＝＝，所以球的体积(2)2＋123V ＝πR 3＝4π.433答案：B3．已知一个几何体的三视图如图所示，则该几何体的体积为( )A. B.323163C.D.8343解析：该几何体由一个三棱锥和一个三棱柱组合而成，直观图如图所示，V ＝V 柱＋V 锥＝×(1＋1)×1×2＋××(1＋1)×1×2＝，故选C.12131283答案：C4．如图，网格纸上小正方形的边长为1，粗线(实线和虚线)表示的是某几何体的三视图，则该几何体外接球的体积为( )A ．24πB ．29πC ．48πD ．58π解析：如图，在3×2×4的长方体中构造符合题意的几何体 (三棱锥A BCD )，其外接球即为长方体的外接球，表面积为4πR 2＝π(32＋22＋42)＝29π.答案：B5．(2018·合肥市质检)如图，网格纸上小正方形的边长为1，实线画出的是某多面体的三视图，则该多面体的体积为( )A ．3B ．32C ．9D ．92解析：由题中的三视图，可得该几何体是一个以俯视图中的梯形为底面的四棱锥，其底面面积S ＝×(2＋4)×1＝3，高h ＝3，故其体积V ＝Sh ＝3，故选A.1213答案：A6．若三棱锥P ABC 的最长的棱PA ＝2，且各面均为直角三角形，则此三棱锥的外接球的体积是________．解析：如图，根据题意，可把该三棱锥补成长方体，则该三棱锥的外接球即该长方体的外接球，易得外接球的半径R ＝PA ＝1，所以该三棱锥的外接球的体积V ＝×π×13＝π.124343答案：π437．已知矩形ABCD 的顶点都在半径为2的球O 的球面上，且AB ＝3，BC ＝，过点D 3作DE 垂直于平面ABCD ，交球O 于E ，则棱锥E ABCD 的体积为________．解析：如图所示，BE 过球心O ，∴DE ＝＝2，42－32－(3)2∴V E －ABCD ＝×3××2＝2.1333答案：238．已知H 是球O 的直径AB 上一点，AH ∶HB ＝1∶2，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为________．解析：如图，设截面小圆的半径为r ，球的半径为R ，因为AH ∶HB ＝1∶2，所以OH ＝R .由勾股定理，有R 2＝r 2＋OH 2，又由题意13得πr 2＝π，则r ＝1，故R 2＝1＋(R )2，即R 2＝.由球的表面积公式，得S ＝4πR 2＝.13989π2答案：9π29．如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置．(1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝，OD ′＝2，求五棱锥D ′­ABCFE 的体积．542解析：(1)证明：由已知得AC ⊥BD ，AD ＝CD .又由AE ＝CF 得＝，故AC ∥EF .AEAD CFCD 由此得EF ⊥HD ，EF ⊥HD ′，所以AC ⊥HD ′.(2)由EF ∥AC 得＝＝.OHDO AEAD 14由AB ＝5，AC ＝6得DO ＝BO ＝＝4.AB 2－AO 2所以OH ＝1，D ′H ＝DH ＝3.于是OD ′2＋OH 2＝(2)2＋12＝9＝D ′H 2，2故OD ′⊥OH .由(1)知，AC ⊥HD ′，又AC ⊥BD ，BD ∩HD ′＝H ，所以AC ⊥平面BHD ′，于是AC ⊥OD ′.又由OD ′⊥OH ，AC ∩OH ＝O ，所以OD ′⊥平面ABC .又由＝得EF ＝.EFAC DHDO 92五边形ABCFE 的面积S ＝×6×8－××3＝.121292694所以五棱锥D ′­ABCFE 的体积V ＝××2＝.136942232210.(2018·莆田质检)如图，在四棱锥S ABCD 中，四边形ABCD 为矩形，E 为SA 的中点，SA ＝SB ＝2，AB ＝2，BC ＝3.3(1)证明：SC ∥平面BDE ；(2)若BC ⊥SB ，求三棱锥C BDE 的体积．解析：(1)证明：连接AC ，设AC ∩BD ＝O ，∵四边形ABCD 为矩形，则O 为AC 的中点．在△ASC 中，E 为AS 的中点，∴SC ∥OE ，又OE 平面BDE ，SC 平面BDE ，∴SC ∥平面BDE .(2)∵BC ⊥AB ，BC ⊥SB ，AB ∩SB ＝B ，∴BC ⊥平面SAB ，又BC ∥AD ，∴AD ⊥平面SAB .∵SC ∥平面BDE ，∴点C 与点S 到平面BDE 的距离相等，∴V C BDE ＝V S BDE ＝V D SBE ，在△ABS 中，SA ＝SB ＝2，AB ＝2，3∴S △ABS ＝×2×1＝.1233又∵E 为AS 的中点，∴S △BES ＝S △ABS ＝.1232又点D 到平面BES 的距离为AD ，∴V D BES ＝S △BES ·AD ＝××3＝，13133232∴V C BDE ＝，即三棱锥C BDE 的体积为.3232B 组——能力提升练1．(2018·湖北七市联考)一个几何体的三视图如图所示，该几何体外接球的表面积为( )A ．36π B.π1123C ．32πD ．28π解析：根据三视图，可知该几何体是一个四棱锥，其底面是一个边长为4的正方形，高是2.将该四棱锥补形成一个三棱柱，如图所示，则其底面是边长为4的正三角形，高是4，3该三棱柱的外接球即为原四棱锥的外接球．∵三棱柱的底面是边长为4的正三角形，∴底面三角形的中心到该三角形三个顶点的距离为×2＝，∴外接球的半径R ＝233433＝，外接球的表面积S ＝4πR 2＝4π×＝，故选B.(433)2＋22283283112π3答案：B2．(2018·广州模拟)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马；将四个面都为直角三角形的三棱锥称为鳖臑．若三棱锥P ABC 为鳖臑，PA ⊥平面ABC ，PA ＝AB ＝2，AC ＝4，三棱锥P ABC 的四个顶点都在球O 的球面上，则球O 的表面积为( )A ．8π B ．12πC ．20πD ．24π解析：如图，因为四个面都是直角三角形，所以PC 的中点到每一个顶点的距离都相等，即PC 的中点为球心O ，易得2R ＝PC ＝，所以R ＝，球O 的表面积为4πR 2＝20π，20202选C.答案：C3．在封闭的直三棱柱ABC ­A 1B 1C 1内有一个体积为V 的球．若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A ．4π B.9π2C ．6πD.32π3解析：由题意可得若V 最大，则球与直三棱柱的部分面相切，若与三个侧面都相切，可求得球的半径为2，球的直径为4，超过直三棱柱的高，所以这个球放不进去，则球可与上下底面相切，此时球的半径R ＝，该球的体积最大，V max ＝πR 3＝×＝.32434π32789π2答案：B4．四棱锥S ABCD 的所有顶点都在同一个球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥体积取得最大值时，其表面积等于8＋8，则球O 的体积等于( )3A. B.32π3322π3C ．16πD.162π3解析：依题意，设球O 的半径为R ，四棱锥S ABCD 的底面边长为a 、高为h ，则有h ≤R ，即h 的最大值是R ，又AC ＝2R ，则四棱锥S ABCD 的体积V S ABCD ＝×2R 2h ≤.因132R 33此，当四棱锥S ABCD 的体积最大，即h ＝R 时，其表面积等于(R )2＋4××R × 2122＝8＋8，解得R ＝2，因此球O 的体积等于＝，选A.(2R2)2＋R 234πR 3332π3答案：A5．(2017·河北质量监测)多面体的三视图如图所示，则该多面体的体积为________cm 3.解析：由三视图可知该几何体是一个三棱锥，如图所示，在三棱锥D ABC 中，底面ABC 是等腰三角形，设底边AB 的中点为E ，则底边AB 及底边上的高CE 均为4，侧棱AD ⊥平面ABC ，且AD ＝4，所以三棱锥D ABC 的体积V ＝S △13ABC ·AD ＝××4×4×4＝(cm 3)．1312323答案：3236．已知正四棱锥O ABCD 的体积为，底面边长为，则以O 为球心，OA 为半径的球3223的表面积为________．解析：过O 作底面ABCD 的垂线段OE (图略)，则E 为正方形ABCD 的中心．由题意可知×()2×OE ＝，所以OE ＝，故球的半径R ＝OA ＝＝，则球的表面133322322OE 2＋EA 26积S ＝4πR 2＝24π.答案：24π7．如图，已知正三棱锥P ­ABC 的侧面是直角三角形，PA ＝6.顶点P 在平面ABC 内的正投影为点D ，D 在平面PAB 内的正投影为点E ，连接PE 并延长交AB 于点G .(1)证明：G 是AB 的中点；(2)在图中作出点E 在平面PAC 内的正投影F (说明作法及理由)，并求四面体PDEF 的体积．解析：(1)证明：因为P 在平面ABC 内的正投影为D ，所以AB ⊥PD .因为D 在平面PAB 内的正投影为E ，所以AB ⊥DE .因为PD ∩DE ＝D ，所以AB ⊥平面PED ，故AB ⊥PG .又由已知，可得PA ＝PB ，所以G 是AB 的中点．(2)在平面PAB 内，过点E 作PB 的平行线交PA 于点F ，F 即为E 在平面PAC 内的正投影．理由如下：由已知可得PB ⊥PA ，PB ⊥PC ，又EF ∥PB ，所以EF ⊥PA ，EF ⊥PC .因此EF ⊥平面PAC ，即点F 为E 在平面PAC 内的正投影．连接CG ，因为P 在平面ABC 内的正投影为D ，所以D 是正三角形ABC 的中心．由(1)知，G 是AB 的中点，所以D 在CG 上，故CD ＝CG .23由题设可得PC ⊥平面PAB ，DE ⊥平面PAB ，所以DE ∥PC ，因此PE ＝PG ，DE ＝PC .2313由已知，正三棱锥的侧面是直角三角形且PA ＝6，可得DE ＝2，PE ＝2.2在等腰直角三角形EFP 中，可得EF ＝PF ＝2，所以四面体PDEF 的体积V ＝××2×2×2＝.131243。

2019版高考数学一轮复习第7章立体几何7.1 空间几何体的结构及其三视图和直观图课后作业文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2019版高考数学一轮复习第7章立体几何7.1 空间几何体的结构及其三视图和直观图课后作业文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2019版高考数学一轮复习第7章立体几何7.1 空间几何体的结构及其三视图和直观图课后作业文的全部内容。

7．1 空间几何体的结构及其三视图和直观图[基础送分提速狂刷练]一、选择题1．一个几何体的三视图如图所示,则该几何体的直观图可以是（）答案D解析由俯视图是圆环可排除A，B，C,进一步将已知三视图还原为几何体，故选D.2．如图所示，在正方体ABCD－A′B′C′D′中，M，E是AB的三等分点,G，N是CD的三等分点，F，H分别是BC，MN的中点，则四棱锥A′－EFGH的侧视图为（）答案C解析侧视图中A′E，A′G重合，A′H成为A′N，A′F，A′B重合,侧视图为向左倾斜的三角形．故选C.3．(2017·临沂模拟)如图甲，将一个正三棱柱ABC－DEF截去一个三棱锥A－BCD，得到几何体BCDEF，如图乙，则该几何体的正视图（主视图）是( )答案C解析由于三棱柱为正三棱柱，故平面ADEB⊥平面DEF，△DEF是等边三角形，所以CD在后侧面上的投影为AB的中点与D的连线，CD的投影与底面不垂直．故选C.4．（2018·江西景德镇质检)如图所示，正方体ABCD－A1B1C1D1上、下底面中心分别为O1，O2，将正方体绕直线O1O2旋转一周，其中由线段BC1旋转所得图形是( ）答案D解析由图形的形成过程可知,在图形的面上能够找到直线，在B，D中选,显然B不对,因为BC1中点绕O1O2旋转得到的圆比B点和C1点的小．故选D.5．（2017·内江模拟)如图，已知三棱锥P－ABC的底面是等腰直角三角形，且∠ACB＝错误!，侧面PAB⊥底面ABC，AB＝PA＝PB＝2.则这个三棱锥的三视图中标注的尺寸x，y，z分别是( )A。

课时作业
A 组——基础对点练
1．设 m，n 是不一样的直线，α，β是不一样的平
面，且
m，n α，则“α∥β”是“ m ∥β且 n∥β”的 ()
A．充足不用要条件
C．充要条件
分析：若 m，nα，α∥β，则m∥β
且
B．必需不充足条件
D．既不充足也不用要条件
n∥β；反之若 m， nα，m∥β且n∥β，则α与
β订交或平行，即“α∥β”是“ m∥β且 n∥β”的充足不用要条件．
答案： A
2．设α，β是两个不一样的平面， m，n 是平面α内的两条不一样直线， l1， l2是平面β内的两条订交直线，则α∥β的一个充足不用要条件是 ( )
A． m∥ l1且 n∥l 2 B．m∥β且 n∥l2
C． m∥β且 n∥βD．m∥β且 l1∥α
分析：由 m∥l1，
m α， 1 β，得 1 2 1 2
订交，因此
α∥β，反l l ∥α，同理 l ∥α，又 l ，l
之不建立，因此m∥l1且 n∥l2是α∥β的一个充足不用要条件．
答案： A
3．设α，β是两个不一样的平面， m 是直线且 mα，“m∥β”是“ α∥β”的()
A．充足而不用要条件
B．必需而不充足条件
C．充足必需条件
D．既不充足也不用要条件
分析：若 mα且m∥β，则平面α与平面β不必定平行，有可能订交；而mα且α∥β必定能够推出 m∥β，因此“ m∥β”是“α∥β”的必需而不充足条件．
答案： B
4．已知 m，n 是两条不一样的直线，α，β，γ是三个不一样的平面，则以下命题中正确的是()
A．若α⊥γ，α⊥β，则γ∥β
B．若 m∥n，mα，nβ，则α∥β。

学习资料第七章立体几何第一节空间几何体的结构、三视图和直观图课时规范练A组——基础对点练1．(2020·青岛模拟）以下命题：①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台；②圆柱、圆锥、圆台的底面都是圆面；③一个平面截圆锥，得到一个圆锥和一个圆台．其中正确命题的个数为（)A．0B．1C．2 D．3解析:由圆台的定义可知①错误，②正确．对于命题③，只有平行于圆锥底面的平面截圆锥，才能得到一个圆锥和一个圆台，③不正确．答案：B2．如图（1)所示，是一个棱长为2的正方体被削去一个角后所得到的几何体,其中DD1＝1，AB＝BC＝AA1＝2,若此几何体的俯视图如图（2）所示，则可以作为其主视图的是（)解析：根据该几何体的直观图和俯视图知，其主视图的长应为底面正方形的对角线长，宽应为正方体的棱长，故排除B，D；而在三视图中看不见的棱用虚线表示，故排除A。

答案：C3．一个三角形用斜二测画法画出来的直观图是边长为2的正三角形，则原三角形的面积是()A．2错误!B．4错误!C. 3 D．都不对解析:根据斜二测画法的规则,正三角形的底边长是原三角形的底边长，原三角形的高是正三角形高的2错误!倍,而正三角形的高是错误!，故原三角形的高为2错误!,于是其面积为错误!×2×26＝2错误!.答案：A4.如图，正方体ABCD-A1B1C1D1中，E为棱BB1的中点，用过点A、E、C1的平面截去该正方体的下半部分，则剩余几何体的主视图是(）解析：取DD1的中点F，连接AF,C1F.平面AFC1E为截面．如图：则上半部分的主视图如A选项,故选A。

答案：A5．如图，网格纸的各小格都是正方形，粗实线画出的是一个凸多面体的三视图（两个矩形，一个直角三角形),则这个几何体可能为(）A．三棱台B．三棱柱C．四棱柱D．四棱锥解析:根据三视图的法则：长对正，高平齐，宽相等，可得几何体如图所示，这是一个三棱柱．答案：B6.如图所示，右面的几何体由一个圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得,现用一个竖直的平面去截这个几何体，则截面图形可能是()A．①②B．②③C．③④D．①⑤解析：圆锥的轴截面为等腰三角形,此时①符合条件；当截面不过旋转轴时,圆锥在截面上为双曲线的一支，此时⑤符合条件，故截面图形可能是①⑤。