第十七章 反比例函数复习

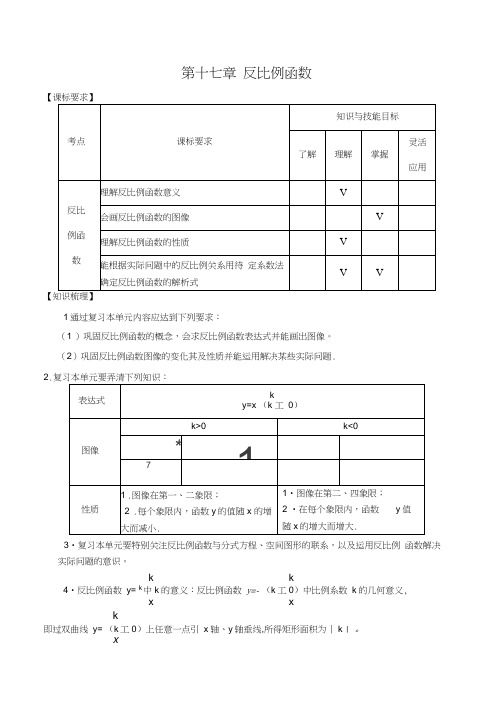
第十七章 反比例函数1通过复习本单元内容应达到下列要求：（1 ）巩固反比例函数的概念，会求反比例函数表达式并能画出图像。

（2）巩固反比例函数图像的变化其及性质并能运用解决某些实际问题. 2.3•复习本单元要特别关注反比例函数与分式方程、空间图形的联系，以及运用反比例 函数解决实际问题的意识。

k k 4•反比例函数 y= k 中k 的意义：反比例函数 y=- （k 工0）中比例系数 k 的几何意义,xxk即过双曲线 y= （k 工0）上任意一点引 x 轴、y 轴垂线,所得矩形面积为丨k | 。

x【能力训练】6.1 .如果双曲线 ym经过点(2 , - 1),那么m= _________________ ；x2 .己知反比例函数 ym 1(x >0) , y 随x 的增大而增大，则m 的取值范围是__________x如图，一次函数 y=kx+b 的图像与反比例函数y=’的图像相交于 A 、B 两点,x(1) 利用图中条件，求反比例函数和一次函数的解析式；(2) 根据图像写出使一次函数的值小于反比例函数的值 x 的取值范围.12y 的图像与一次函数x图像相交于 P 、Q 两点，并且 P 点的纵坐标是 (1) 求这个一次函数的解析式；4 •如果变阻器两端电压不变， 那么通过变阻器的电流 y 与电阻x 的函数关系图像大致是( )如图，已知反比例函数 3.BC(2)求厶POQ的面积. 6.其图像如图所示。

(1)求p 与S 之间的函数关系式；⑵ 求当S=0.5m 2时,物体承受的压强p 。

11.如图，等腰梯形 ABCD 中, AB = CD AD / BC, AD = 2 , BC = 4 ,如果P 是BC 上一点，Q 是AP 上一点，且 AQD 60⑴求证：" ABP s" DQA⑵当点P 在BC 上移动时，线段 DQ 的长度也随之变化，设 之间的函数关系式，并指出x 的取值范围.7 .给出下列函数：(1)y=2x; (2)y=-2x+1; (3)y=的增大而减小的函数是( )—(x>0) (4)y=x xA. ( 1)、(2)B . (1 )、( 3)C .⑵、(4) D—(x<-1)其中，y 随x.(2)、(3)、( 4) k8.设双曲线y=—与直线y=-x+1相交于点xA 、B , O 为坐标原点，则/ AOB 是(A.锐角 B .直角C.钝角D.锐角或钝角49 .如图，在直角坐标系中，直线y=6-x 与函数y= (x>0)的图像相交x于点A 、B ,设点A 的坐标为(x 1, , y 1)，那么长为 X 1,宽为y 1的矩 形面积和周长分别为()A. 4, 12 B . 8, 12 C . 4, 6 D . 8, 6 10 .在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,S(m 2)B 60PA =P C12 .已知：如图，矩形 ABCD 中，AB=5, AD=3, E 是CD 上一点(不与 C D 重合)连接 AE , 过点B 作BF丄AE ,垂足为 F 。

第17章 反比例函数复习练习题（二）一、填空题1．已知反比例函数y=2x的图像经过点A （m ，1）,则m 的值为 。

2．若反比例函数1k y x -=（k 为常数，1k ≠），若点2A (1 )，在这个函数的图象上，求k 的值；若在这个函数图象的每一支上，y 随x 的增大而减小，求k 的取值范围；3.已知反比例函数 y=x m 12+的图象在第一、三象限，则m 的取值范围是 ． 4.在反比例函数1my x -=图象每一条曲线上，y 都随x 的增大而减小，则m 的取值范围 ．5．根据反比例函数xy 3=和一次函数12+=x y 的图象，请写出它们的一个共同点 ________________________ ；一个不同点 _____ _______________ . 6.正比例函数y kx =的图象与反比例函数my x=的图象有一个交点的坐标是（12--，），则另一个交点的坐标为 。

7．若1122()()A x y B x y ，，，是双曲线3y x=上的两点，且120x x >>，则12_______y y . 8．反比例函数xn y 1-=的图象在第二、四象限，则n 的取值范围为 ， ),3(),,2(21y B y A 为图象上两点，则y 1 y 2（用“<”或“>”填空）9．已知点),2(),,1(),,1(321y C y B y A -在反比例函数)0(<=k xky 的图象上，则321,,y y y 的大小关系为 （用“>”或“<”连接） 10．),(),,(2211y x B y x A 都在反比例函数xy 6=图象上。

若321-=x x ，则21y y 的值为 。

11．函数1(0)y x x =≥ , xy 92=(0)x >的图象如图所示，则结论： ① 两函数图象的交 点A 的坐标为（3 ,3 ) ② 当3x >时，21y y > ③ 当 1x =时， BC = 8 ④当 x 逐渐增 大时，1y 随着x 的增大而增大，2y 随着x 的增大而减小．其中正确结论的序号是 .12．两个反比例函数k y x =和1y x =在第一象限内的图象如图7所示，点P 在ky x=的图象上，PC ⊥x 轴于点C ，交1y x =的图象于点A ，PD ⊥y 轴于点D ，交1y x =的图象于点B ，当点P 在ky x=的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化；③PA 与PB 始终相等；其中一定正确的是 .13．函数y= 4x 和y=1x 在第一象限内的图像如图，点P 是y= 4x 的图像上一动点，PC⊥x 轴于点C ，交y=1x的图像于点B.给出如下结论：①△ODB 与△OCA 的面积相等；②PA 与PB 始终相等；③四边形PAOB 的面积大小不会发生变化；④CA= 13AP.其中所有正确结论的序号是______________.14.如图，一次函数y 1=ax+b （a ≠0）与反比例函数y 2=()0≠k xk的图象交于A （1,4）、B （4,1）两点，若y 1＞y 2，则x 的取值范围是15.近视眼镜的度数y (度)与镜片焦距x (m )成反比例(即)0(≠=k xky )，已知200度近视眼镜的镜片焦距为m 5.0,则y 与x 之间的函数关系式是 . 16.反比例函数ky =x的图象与一次函数21y =x +的图象的一个交点是(1，k )，则反比例函数的解析式是 ．17. 14、点P 在反比例函数)0(≠=k xky 的图像上，点Q （2,4）与点P 关于y 轴对称，则反比例函数的解析式为18.若点Ｐ()2,a 在一次函数42+=x y 的图象上，它关于y 轴的对称点在反比例函数xky =的图象上，则反比例函数的解析式为 . 19.已知点()P a b ，在反比例函数2y x =的图象上，若点P 关于y 轴对称的点在反比例函数k y x=的图象上，则k 的值为____________.20.若一次函数的图象经过反比例函数4y x=-图象上的两点（1，m ） 和（n ，2），则这个一次函数的解析式是 _.21.已知：多项式x 2－kx ＋1是一个完全平方式，则反比例函数y =1k x-的解析式为_ __。

第十七章 反比例函数
1.定义：形如x k
y =（k 为常数，k≠0）的函数称为反比例函数。

反比例函数的其他形式xy=k 1-=kx y x
k y 1= 2.图像：反比例函数的图像属于双曲线。

反比例函数的图象既是轴对称图形又是中心对称图形。

有两条对称轴：直线y=x 和 y=-x 。

对称中心是：原点
3.性质:当k ＞0时双曲线分别位于第一、第三象限，在每个象限内y 值随x 值的增大而减小；如：图1 当k ＜0时双曲线分别位于第二、第四象限，在每个象限内y 值随x 值的增大而增大。

如：图2
4.|k|的几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积。

图3
5. 反比例函数解析式的球阀：待定系数法
先根据题意设出函数解析式，再根据条件求出常数k 或b 系数，从而写出这个函数解析式的方法叫做待定系数法.可用待定系数法求一次函数和反比例函数的解析式
图2 图3
图1
6. 反比例函数知识结构图。

第⼗七章_反⽐例函数__复习教学案第⼗七章反⽐例函数⼀、知识点与⽅法（⼀）反⽐例函数的意义（1）⼀般地，形如的函数称为反⽐例函数，其中，⾃变量x 的取值范围是。

（2）反⽐例函数的特点是：①②③（3）反⽐例函数除了⼀般形式外，它的表达形式还有、。

【练习】1、下列哪个等式中的y 是x 的反⽐例函数？① y = 4x ②y = -2x -1 ③ y = 6x + 1 ④ xy = 123 ⑤ x y = 3 ⑥xy 2-= ⑦ 25+=x y ⑧ x y 23-= ⑨ 31+=x y ⑩ 28xy = （11） x ay = 2、已知点（1，-2）在反⽐例函数y ＝kx的图象上，则k=_______3、（2010·凉⼭）已知函数52)2(--=mx m y 是反⽐例函数，求m 的值？4、已知y 是x 的反⽐例函数，当x ＝2时，y ＝8，写出y 与x 的关系式，并求当y ＝－4时，x 的值。

5、y 与x 成正⽐例，x 与z 成反⽐例，那么y 与z 成什么函数？写出推理过程。

（⼆）反⽐例函数的图象和性质（1）反⽐例函数y ＝kx （k 为常数，且0k ≠）的图象是。

（2）反⽐例函数y ＝x 6的两个分⽀关于对称；在同⼀直⾓坐标系中，反⽐例函数y ＝x 6与y ＝—x6的图象关于对称。

（3）完成表格说明：表格中划线的内容还可以说成。

【练习】4、反⽐例函数4y x =-的图象⼤致是（）5、如果函数y=kx-2（k ≠0）的图象不经过第⼀象限，那么函数ky x=的图象⼀定在( ) A.第⼀、⼆象限 B.第三、四象限 C.第⼀、三象限 D.第⼆、四象限 6、函数)1(+=x k y 和xky -=（k ≠0）在同⼀坐标系中的⼤致图象是（? ）A B C D 7、函数y kx =-与y k x=（k ≠0）的图象的交点个数是（）A 、0B 、1C 、2D 、不确定 8、已知反⽐例函数()0ky k x=<的图象上有两点A（1x ，1y ），B （2x ，2y ），且12x x <则12y y -的值是（）A 、正数B 、负数C 、⾮正数D 、不能确定 9、正⽐例函数y = k 1x （k ≠0）和反⽐例函数y = xk 2（k ≠0）的的⼀个交点坐标为（1，—3），则另⼀个交点坐标为。

八年级下册数学十七章知识点数学，是研究数量、结构、变化、空间以及信息等概念的一门学科。

不同的数学家对数学的确切范围有不同看法。

下面是整理的八年级下册数学十七章知识点，仅供参考希望能够帮助到大家。

八年级下册数学十七章知识点反比例函数的定义定义：形如函数y=k/x(k为常数且k≠0)叫做反比例函数，其中k叫做比例系数，x是自变量，y是自变量x的函数，x的取值范围是不等于0的一切实数。

反比例函数的性质函数y=k/x 称为反比例函数，其中k≠0，其中X是自变量，1.当k0时，图象分别位于第一、三象限，同一个象限内，y随x的增大而减小;当k0时，图象分别位于二、四象限，同一个象限内,y随x的增大而增大。

2.k0时，函数在x0上同为减函数、在x0上同为减函数;k0时，函数在x0上为增函数、在x0上同为增函数。

3.x的取值范围是：x≠0;y的取值范围是：y≠0。

4..因为在y=k/x(k≠0)中，x不能为0，y也不能为0，所以反比例函数的图象不可能与x轴相交，也不可能与y轴相交。

但随着x无限增大或是无限减少，函数值无限趋近于0，故图像无限接近于x轴5. 反比例函数的图象既是轴对称图形，又是中心对称图形，它有两条对称轴y=x y=-x(即第一三，二四象限角平分线)，对称中心是坐标原点。

反比例函数的一般形式一般地，如果两个变量x、y之间的关系可以表示成(k为常数，k≠0)的形式，那么称y是x的反比例函数。

其中，x是自变量，y是函数。

由于x在分母上，故取x≠0的一切实数，看函数y的取值范围，因为k≠0，且x≠0，所以函数值y也不可能为0。

补充说明：1.反比例函数的解析式又可以写成：(k是常数，k≠0).2.要求出反比例函数的解析式，利用待定系数法求出k即可.反比例函数解析式的特征⑴等号左边是函数，等号右边是一个分式。

分子是不为零的常数(也叫做比例系数)，分母中含有自变量，且指数为1。

⑴比例系数⑴自变量的取值为一切非零实数。