扫描线填充算法--有效边表填充算法
- 格式:doc
- 大小:63.00 KB
- 文档页数:6

扫描线多边形填充算法扫描线多边形填充算法(Scanline Polygon Fill Algorithm)是一种计算机图形学中广泛使用的算法,用于将一个封闭的多边形形状涂色填充。
它通过扫描线的方式,从上到下将多边形内的像素按照预设的填充颜色来进行填充。
本文将详细介绍扫描线多边形填充算法的原理、流程和实现细节。
1.算法原理:扫描线多边形填充算法基于扫描线的思想,在水平方向上扫描每一行像素,并检测多边形边界与扫描线的交点。
通过将扫描线从上到下扫过整个多边形,对于每一行像素,找出与多边形边界交点的水平线段,然后根据填充颜色将像素点进行填充。
2.算法流程:-找出多边形的最小和最大Y坐标,确定扫描线的范围。
-从最小Y坐标开始,到最大Y坐标结束,逐行进行扫描。
-对于每一行,找出与多边形边界交点的水平线段。
-根据填充颜色,为每个水平线段上的像素点进行填充。
3.算法实现:-首先,需要根据给定的多边形描述边界的顶点坐标,计算出每条边的斜率、最小和最大Y值以及每条边的X坐标交点。
-然后,对于每一扫描线,找出与多边形边界交点的水平线段,即找出交点的X坐标范围。
-最后,根据填充颜色,将该范围内的像素点进行填充。
4.算法优化:- 针对复杂多边形,可以使用活性边表(AET,Active Edge Table)来管理边界信息,加快查找交点的速度。
-可以使用桶排序来排序边界事件点,提高扫描速度。
-根据多边形边的特征,对算法进行优化,减少不必要的计算和内存消耗。
5.算法应用:-扫描线多边形填充算法广泛应用于计算机图形学中的图形渲染、图像处理等领域。
-在游戏开发、CAD绘图、虚拟现实等应用中,扫描线多边形填充算法被用于快速绘制和渲染复杂多边形。
总结:扫描线多边形填充算法是一种经典的计算机图形学算法,通过扫描线的方式对多边形进行填充。
它可以高效地处理各种形状的多边形,包括凸多边形和凹多边形。
算法虽然简单,但在实际应用中具有广泛的用途。


扫描线种子填充算法扫描线种子填充算法的基本过程如下:当给定种子点(x, y)时,首先分别向左和向右两个方向填充种子点所在扫描线上的位于给定区域的一个区段,同时记下这个区段的范围[xLeft, xRight],然后确定与这一区段相连通的上、下两条扫描线上位于给定区域内的区段,并依次保存下来。
反复这个过程,直到填充结束。
扫描线种子填充算法可由下列四个步骤实现:(1) 初始化一个空的栈用于存放种子点,将种子点(x, y)入栈;(2) 判断栈是否为空,如果栈为空则结束算法,否则取出栈顶元素作为当前扫描线的种子点(x, y),y是当前的扫描线;(3) 从种子点(x, y)出发,沿当前扫描线向左、右两个方向填充,直到边界。
分别标记区段的左、右端点坐标为xLeft和xRight;(4) 分别检查与当前扫描线相邻的y - 1和y + 1两条扫描线在区间[xLeft, xRight]中的像素,从xLeft开始向xRight方向搜索,若存在非边界且未填充的像素点,则找出这些相邻的像素点中最右边的一个,并将其作为种子点压入栈中,然后返回第(2)步;这个算法中最关键的是第(4)步,就是从当前扫描线的上一条扫描线和下一条扫描线中寻找新的种子点。
如果新扫描线上实际点的区间比当前扫描线的[xLeft, xRight]区间大,而且是连续的情况下,算法的第(3)步就处理了这种情况。
如图所示:新扫描线区间增大且连续的情况假设当前处理的扫描线是黄色点所在的第7行,则经过第3步处理后可以得到一个区间[6,10]。
然后第4步操作,从相邻的第6行和第8行两条扫描线的第6列开始向右搜索,确定红色的两个点分别是第6行和第8行的种子点,于是按照顺序将(6, 10)和(8, 10)两个种子点入栈。
接下来的循环会处理(8, 10)这个种子点,根据算法第3步说明,会从(8, 10)开始向左和向右填充,由于中间没有边界点,因此填充会直到遇到边界为止,所以尽管第8行实际区域比第7行的区间[6,10]大,但是仍然得到了正确的填充。
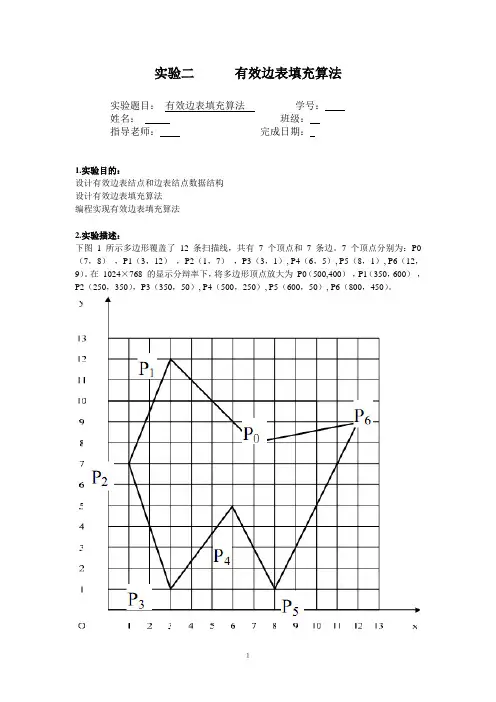
实验二有效边表填充算法实验题目:有效边表填充算法学号:姓名:班级:指导老师:完成日期:1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图1 所示多边形覆盖了12 条扫描线,共有7 个顶点和7 条边。
7 个顶点分别为:P0(7,8),P1(3,12),P2(1,7),P3(3,1), P4(6,5), P5(8,1), P6(12,9)。
在1024×768 的显示分辩率下,将多边形顶点放大为P0(500,400),P1(350,600),P2(250,350),P3(350,50), P4(500,250), P5(600,50), P6(800,450)。
图1示例多边形图2屏幕显示多边形3.算法设计:多边形的有效边表填充算法的基本原理是按照扫描线从小到大的移动顺序,计算当前扫描线与多边形各边的交点,然后把这些交点按x值递增的顺序进行排序、配对,以确定填充区间,然后用指定颜色点亮填充区间的所有像素,即完成填充工作。
有效边表填充算法通过访问多边形覆盖区间内的每个像素,可以填充凸、凹多边形和环,已成为目前最为有效的多边形填充算法。
4.源程序:1)//AET.h和AET..cppclass AET{public:AET();virtual ~AET();double x;int yMax;double k; //代替1/kAET *next;}2)//Bucket.h和Bucket.cppclass Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;}3) // TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数,顶点存放在整型二维数组Point[N]中class CTestView : public CView{。

区域填充的扫描线算法区域填充是一种常见的计算机图形学算法,用于将一个封闭区域内的所有像素点填充为指定的颜色。
扫描线算法是区域填充的一种常用方法,本文将介绍扫描线算法的基本原理、实现步骤和一些优化技巧。
扫描线算法的基本原理是利用扫描线从图像的上边界向下扫描,检测每个扫描线与区域的交点。
当遇到一个交点时,根据该交点的左右两侧的交点情况,确定将该交点连接到哪个交点上。
通过不断地扫描和连接交点,最终将整个区域填充为指定的颜色。
下面是扫描线算法的具体实现步骤:1.首先需要确定区域的边界,可以由用户提供或通过其他算法生成。
边界可以用一系列的线段、多边形或曲线表示。
2. 创建一个数据结构来存储每个扫描线与区域的交点。
常用的数据结构是活性边表(Active Edge Table,AET)和扫描线填充表(Scanline Fill Table,SFT)。
AET用于存储当前扫描线与区域边界的交点,SFT用于存储所有扫描线的交点。
3.初始化扫描线的起始位置为图像的上边界,并创建一个空的AET。
4.开始扫描线的循环,直到扫描线到达图像的下边界。
每次循环都进行以下操作:-将扫描线与区域边界进行相交,找出所有与区域相交的线段,并将它们的交点加入到AET中。
-对AET按照交点的x坐标进行排序。
-从AET中取出相邻的两个交点,根据这两个交点之间的像素点是否在区域内来决定是否填充这些像素点。
5.当扫描线到达图像的下边界时,完成填充。
扫描线算法的实现可能会遇到一些边界情况和优化需求。
下面是一些常见的优化技巧:1.边界处理:在AET中存储的交点需要进行边界处理,确保交点处于图像范围内。
2.垂直线段处理:对于垂直线段,可以进行特殊处理,避免在AET中重复存储相同的交点。
3.区域内部边界处理:当区域内部有不连续的边界时,需要对交点进行合并,避免出现多余的像素点填充。
4.使用扫描线填充算法优化:对于大尺寸的区域填充,可以使用扫描线填充算法进行优化。

有效边表填充算法基本思想:⽤⽔平扫描线从上到下(或从下到上)扫描由多条⾸尾相连的线段构成的多边形,每根扫描线与多边形的某些边产⽣⼀系列的交点。
将这些交点按照x坐标排序,将排序后的点两两配对,作为线段的两个端点,以所填的颜⾊画⽔平直线。
步骤1.求交,计算扫描线与多边形的交点。
2.交点排序,对第1步得到的交点按照x从⼩到⼤排序3.颜⾊填充,对排序后的交点两两组成⼀个⽔平线段,以画线段的⽅式进⾏颜⾊填充。
4.完成多边形扫描,就结束算法,否则,继续1有效边多边形与当前扫描线相交的边成为有效边(active edge)。
在处理⼀条扫描线时仅对有效边进⾏求交运算,避免与多边形所有边求交,提⾼效率。
x y max1/k next桶表与边表有效边给出了扫描线与有效边交点的计算⽅法,但没有给出新边出现的位置坐标。
为了确定在哪条扫描线上加⼊了新边,就需要构造⼀个边表(edge table ET),⽤以存放扫描线上多边形各条边出现的信息。
⽔平边本⾝就是扫描线在建⽴边表时可以不予考虑。
桶表与边表的表⽰法桶表是按照扫描线顺序管理边出现的⼀个数据结构。
⾸先,构造⼀个纵向扫描线链表,链表的长度为多边形所占有的最⼤扫描线数,链表的每个节点称为桶(bucket),对应多边形覆盖的每⼀条扫描线。
将每条边的信息链加⼊该边最⼩y坐标对应的桶处。
对每⼀条扫描线,如果新增多条边,按照x|y min 坐标递增的顺序存放在⼀个链表中,若x|y min 相等,则按照1/k递增,就形成边表。
x|ymin ymax1/k next。
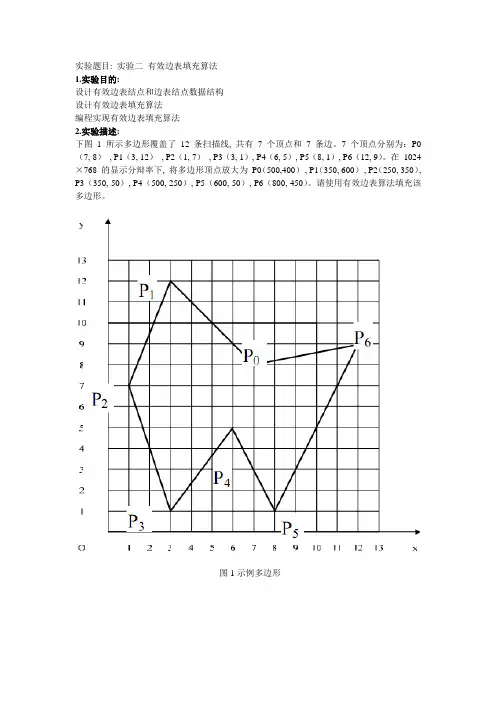
实验题目: 实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线, 共有7 个顶点和7 条边。
7 个顶点分别为:P0(7, 8), P1(3, 12), P2(1, 7), P3(3, 1), P4(6, 5), P5(8, 1), P6(12, 9)。
在1024×768 的显示分辩率下, 将多边形顶点放大为P0(500,400), P1(350, 600), P2(250, 350), P3(350, 50), P4(500, 250), P5(600, 50), P6(800, 450)。
请使用有效边表算法填充该多边形。
图1示例多边形图2 屏幕显示多边形3.算法设计:(1)建立AET和BUCKET类;(2)初始化桶, 并在建立桶结点时为其表示的扫描线初始化为带头结点的链表;(3)对每个桶结点进行循环, 将桶内每个结点的边表合并为有效边表, 并进行有效边表循环;(4)按照扫描线从小到大的移动顺序, 计算当前扫描线与多边形各边的交点, 然后把这些交点按X值递增的顺序进行排序, 配对, 以确定填充区间;(5)用指定颜色点亮填充区间内的所有像素, 即完成填充工作。
4.源程序:1)//AET.hclass AET{public:AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h"class Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数, 顶点存放在整型二维数组Point[N]中class CTestView : public CView{。

实验六扫描线填充算法一、实验目的编写多边形的扫描线填充算法程序,加深对扫描线算法的理解,验证算法的正确性。
二、实验任务(2学时)编写多边形的扫描线填充算法程序,利用数组实现AET,考虑与链表实现程序的不同。
三、实验内容1、算法对一条扫描线的填充一般分为以下4个步骤:(1)求交:计算扫描线与多边形各边的交点;(2)排序:把扫描线上所有交点按递增顺序进行排序;(3)配对:将第一个交点与第二个交点,第三个交点与第四个交点等等进行配对,每对交点代表扫描线与多边形的一个相交区间。
(4)着色:把区间内的像素置为填充色。
2、成员函数的关系主程序名为fill_area(count, x, y),其中参数x, y是两个一维数组,存放多边形顶点(共c ount个)的x和y坐标。
它调用8个子程序,彼此之间的调用关系图1所示为:图1 fill_area的程序结构3、算法的程序设计步骤1:创建“S_L_Fill”工程文件;步骤2:创建类class:“EACH_ENTRY”。
在工作区“S_L_Fill classes”单击右键-→“new class”-→选择类型“Generic Class”名称为“EACH_ENTRY”,添加成员变量(添加至“class EACH_ENTRY { public:”之内):int y_top;float x_int;int delta_y;float x_change_per_scan;步骤3:包含头文件,同时初始化定义多边形顶点数目。
在“class CS_L_FillView : public Cview……”之前添加代码“#include EACH_ENTRY.h”及“#define MAX_POINT 9”。
#define MAX_POINT 9#include "EACH_ENTRY.h"步骤4:在类“class CS_L_FillView”中添加成员变量(鼠标双击工作区“CS_L_FillView”,代码添加至“class CS_L_FillView : public Cview {protected: ……public:之后”):EACH_ENTRY sides[MAX_POINT];int x[MAX_POINT],y[MAX_POINT];int side_count,first_s,last_s,scan,bottomscan,x_int_count;步骤5:利用构造函数“CS_L_FillView::CS_L_FillView()”初始化顶点坐标(鼠标双击工作区“CS_L_FillView”,代码添加至“CS_L_FillView()之内”):x[0]=200;y[0]=100;x[1]=240;y[1]=160;x[2]=220;y[2]=340;x[3]=330;y[3]=100;x[4]=400;y[4]=180;x[5]=300;y[5]=400;x[6]=170;y[6]=380;x[7]=120;y[7]=440;x[8]=100;y[8]=220;步骤6:在“class CS_L_FillView”下添加实现不同功能的成员函数。


多边形区域填充算法--扫描线填充算法(有序边表法)有代码⼆、扫描线算法(Scan-Line Filling)转载 https:///u013044116/article/details/49737585扫描线算法适合对⽮量图形进⾏区域填充,只需要直到多边形区域的⼏何位置,不需要指定种⼦点,适合计算机⾃动进⾏图形处理的场合使⽤,⽐如电脑游戏和三维CAD软件的渲染等等。
对⽮量多边形区域填充,算法核⼼还是求交。
⼀⽂给出了判断点与多边形关系的算法――扫描交点的奇偶数判断算法,利⽤此算法可以判断⼀个点是否在多边形内,也就是是否需要填充,但是实际⼯程中使⽤的填充算法都是只使⽤求交的思想,并不直接使⽤这种求交算法。
究其原因,除了算法效率问题之外,还存在⼀个光栅图形设备和⽮量之间的转换问题。
⽐如某个点位于⾮常靠近边界的临界位置,⽤⽮量算法判断这个点应该是在多边形内,但是光栅化后,这个点在光栅图形设备上看就有可能是在多边形外边(⽮量点没有⼤⼩概念,光栅图形设备的点有⼤⼩概念),因此,适⽤于⽮量图形的填充算法必须适应光栅图形设备。
2.1扫描线算法的基本思想扫描线填充算法的基本思想是:⽤⽔平扫描线从上到下(或从下到上)扫描由多条⾸尾相连的线段构成的多边形,每根扫描线与多边形的某些边产⽣⼀系列交点。
将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜⾊画⽔平直线。
多边形被扫描完毕后,颜⾊填充也就完成了。
扫描线填充算法也可以归纳为以下4个步骤:(1)求交,计算扫描线与多边形的交点(2)交点排序,对第2步得到的交点按照x值从⼩到⼤进⾏排序;(3)颜⾊填充,对排序后的交点两两组成⼀个⽔平线段,以画线段的⽅式进⾏颜⾊填充;(4)是否完成多边形扫描?如果是就结束算法,如果不是就改变扫描线,然后转第1步继续处理;整个算法的关键是第1步,需要⽤尽量少的计算量求出交点,还要考虑交点是线段端点的特殊情况,最后,交点的步进计算最好是整数,便于光栅设备输出显⽰。
扫描线区域填充算法算法步骤如下:1.找到图形区域的上下边界:-遍历图形的所有边界点,找到最大纵坐标和最小纵坐标,确定扫描线的上下边界。
2.初始化扫描线列表:-从上到下依次生成扫描线,建立一个扫描线列表。
3.计算扫描线与图形的交点:-遍历扫描线列表中的每个扫描线,与图形的所有边界进行求交。
-如果与边界有交点,将交点的横坐标存入一个集合中,集合中的数据按从小到大排序。
4.进行填充:-遍历扫描线列表中的每个扫描线,找到对应的交点集合。
-将集合中的每两个横坐标之间的像素点进行填充。
以下是对算法的详细解释:首先,我们需要遍历所有边界点,找到最大纵坐标和最小纵坐标。
这样就确定了我们需要扫描的区域范围,也就是扫描线的上下边界。
接下来,我们生成一个扫描线列表。
从上到下依次生成每一条扫描线,将其存储在扫描线列表中。
然后,对于每一条扫描线,我们需要计算该扫描线与图形的交点。
我们遍历图形的所有边界,并与当前扫描线进行求交。
如果与边界有交点,我们将交点的横坐标存入一个集合中。
这个集合中的数据按从小到大排序,以便后续的填充操作。
最后,我们对于每一条扫描线,找到对应的交点集合。
我们遍历集合中的每两个横坐标之间的像素点,将其进行填充。
这可以通过修改像素的颜色或设置像素的属性来实现。
总结一下,扫描线区域填充算法通过逐行扫描图形区域,计算每行与区域内部的交点,然后进行填充。
该算法的优点是简单、高效,适用于填充简单凸多边形等闭合图形。
然而,该算法对于非凸多边形或包含内孔的图形表现较差,可能需要额外的处理逻辑。
扫描线区域填充算法算法步骤如下:1.首先需要定义一个边表(ET)和活动边表(AET)。
-边表是存储多边形所有边的一张表格,将每条边的y坐标、x坐标以及斜率存储起来。
-活动边表是指当前扫描线与多边形边的交点,它是一个按照x坐标排列的列表。
2.初始化边表(ET)和活动边表(AET)。
-通过遍历多边形的边,将边表中存储对应的边信息。
-初始时活动边表为空。
3.根据多边形的顶点,将边添加到边表中。
-对于每条边,计算出其斜率,以及y坐标的最小值和最大值。
4.进行扫描线填充:a.设置当前扫描线的y坐标,从最小的y值开始,逐行向下扫描。
b.遍历边表,将与当前扫描线相交的边添加到活动边表中。
c.按照x坐标对活动边表进行排序。
d.遍历活动边表,两两配对,填充对应的像素点。
e.过滤掉扫描线下方的边。
f.更新活动边表,将不再与当前扫描线相交的边从活动边表中删除。
5.重复步骤4,直到扫描完整个区域。
然而,扫描线区域填充算法也存在一些局限性和问题:-对于包含小尺寸多边形的大区域填充,算法的迭代次数会增加,导致填充时间变长。
-在多边形内有重叠区域时,算法无法区分内外部,可能导致填充错误。
-当多边形内有孔洞时,算法无法正确填充孔洞。
为了解决以上问题,可以采用一些优化策略来改进算法性能和填充效果。
例如,可以使用边表索引和活动边表的双向链表结构,减少查找和插入操作的时间开销。
此外,还可以使用扫描线的上下两根线段来同时填充两个相邻区域,提高填充速度。
总结起来,扫描线区域填充算法是一种常用且有效的图形填充算法,通过逐行扫描和交点判断来填充封闭区域。
它可以广泛应用于计算机图形学领域,如图形渲染、图像处理等。
算法在实际应用中需根据具体场景进行优化和改进,以满足不同需求。
多边形的填充——扫描线算法(原理)2007年10月05日星期五 11:52多边形在计算机中有两种表示:点阵表示和顶点表示。
顶点表示是用多边形的顶点的序列来描述多边形,该表示几何意义强、占内存少,但它不能直观地说明哪些像素在多边形内。
点阵表示是用位于多边形内的象素的集合来刻划多边形,该方法虽然没有多边形的几何信息,但具有面着色所需要的图像表示形式。
多边形填充就是把多边形的顶点表示转换为点阵表示,即从多边形的给定边界出发,求出位于其内部的各个像素,并将帧缓冲器内的各个对应元素设置为相应的灰度或颜色。
多边形填充最常用的方法就是扫描线算法。
下面分两篇文章介绍这种算法的原理和具体实现。
这里所介绍的算法只是针对非自交多边形,这些多边形可以是凸的、凹的或者带有空洞的。
所谓扫描线算法就是找到多边形的最小y值和最大y值,然后用这个范围内的每一条水平线与多边形相交,求得交点,再绘制线段。
所以我们只需要对一条水平线进行分析就可以。
很显然,一条扫描线和多边形有偶数个交点,将这些交点按照x值从小到大排列,然后取第1、2个绘制,第3、4个绘制......直到所有交点都被取完。
所以,对于一条扫描线,我们需要做的工作可以分为三个步骤:1)求出扫描线与多边形边的交点 2)将交点按照x升序排列 3)将排好序的交点两两配对,然后绘制相应线段。
这三个步骤中,后两个步骤很简单,没有特别的内容需要介绍。
但是第一个步骤比较麻烦。
这里有几个问题需要解决。
一是当扫描线与顶点相交时,交点的取舍。
当与那个顶点关联的边在扫描线同侧时,交点自然算两次,当与那个顶点关联的边在扫描线两侧时,交点只能算一次。
我们使用“下闭上开”的办法。
二是多边形边界上的像素取舍,我们采用“左闭右开”的办法。
三是如何减少计算量。
在绘制直线时,有一种DDA算法,它是利用(x,y)直接求出下一个点位于(x+1,y+m)或者(x+1/m, y+1)。
在这里可以利用这一点。
当已经得到y = e和多边形所有边的交点时,对于下一条扫描线y=e+1,如果没有新边与y=e+1相交,就可以推出y = e+1 和多边形所有边的交点。
区域填充算法区域填充算法
下面将介绍两种常见的区域填充算法:扫描线填充算法和种子填充算法。
1. 扫描线填充算法(Scanline Fill Algorithm):
-扫描线填充算法基于扫描线的原理,从图像的上方向下扫描,对每条扫描线上的像素进行填充。
-算法流程如下:
-选择一个初始扫描线,例如选择图像的最上面一条扫描线;
-遍历该扫描线上的每一个像素,判断是否需要填充该像素;
-如果需要填充,则向区域内部延伸扫描线,同时判断该扫描线上的相邻像素是否需要填充;
-一直延伸扫描线,直到整个区域被填充完毕。
-扫描线填充算法的优点是简单、易于实现,但是算法的效率较低,在处理大尺寸区域时耗时较长。
2. 种子填充算法(Seed Fill Algorithm):
-种子填充算法基于种子点的概念,选择一个起始点作为种子点,然后根据预设的填充规则进行填充。
-算法流程如下:
-选择一个起始点作为种子点,将该点填充上颜色;
-判断该种子点的相邻像素是否需要填充,如果需要则将其填充;
-一直延伸填充,直到整个区域被填充完毕。
-种子填充算法的优点是效率较高,能够处理较大的区域,但是需要选择合适的填充规则,否则可能会导致填充区域不准确或者出现漏填的情况。
以上两种区域填充算法在实际应用中会根据具体的场景和需求选择合适的算法进行使用。
在实际实现时,还需要考虑一些特殊情况,如图像边界处理、扫描顺序等,以确保算法的正确性和效率。
代码:
draw.cpp
//using OpenGL
#include "opengl.h"
#include <iostream>
#include <vector>
#include <algorithm>
#include <unistd.h>
#define PN 6
int
point[N][2]={{40,5},{75,40},{60,70},{35,50},{25,80},{5,30 }};
//AE
struct AE{
AE(float _x,float _dx,int
_ymax){x=_x;dx=_dx;ymax=_ymax;}
float x;
float dx;
int ymax;
void operator++(int){
x+=dx;
}
};
//AET
//which eage is on the right
bool fill_comp(const AE& ae1,const AE& ae2){
if(ae1.x<ae2.x){
return true;
}
if(ae1.x==ae2.x&&ae1.dx<ae2.dx){
return true;
}
return false;
}
void fillline(int y,int x1,int x2){
for(int i=x1;i<=x2;i++) drawpoint(i,y);
flush();
}
void fill(){
//make k=(x2-x1)/(y2-y1)
float k[PN]={0.0};for(int
i=0;i!=PN;i++){k[i]=((float)(point[(i+1)%PN][0]-point[i][ 0])/(float)(point[(i+1)%PN][1]-point[i][1]));}
//find min and max with selection sort.
int min=point[0][1],max=min;for(int
i=0;i!=PN;i++){if(point[i][1]>max){max=point[i][1];};;if( point[i][1]<min){max=point[i][1];}}
//make scanning line list
std::vector<AE>*ET =new std::vector<AE>[max-min+1];
//make ET
//
for(int i =0; i<PN;++i){
//get ymin, ymax
int yminn=point[i][1]<point[(i+1)%PN][1]? i :
(i+1)%PN;
int ymaxn=point[i][1]>=point[(i+1)%PN][1]? i :
(i+1)%PN;
AE *tmp =new
AE(point[yminn][0],k[i],point[ymaxn][1]);
//insert node
ET[point[yminn][1]-min].push_back(*tmp);
}
//init AET
std::vector<AE> AET;
for(int i=0;i!=max-min+1;i++){
//insert node from ET to AET
for(int ii=0;ii!=ET[i].size();ii++){
//sort with selection sort.
AET.insert(std::upper_bound(AET.begin(),
AET.end(),ET[i][ii],fill_comp),ET[i][ii]);
}
//delete y=ymax,"下闭上开"
for(int
ii=0;ii!=AET.size();){if(i+min==AET[ii].ymax)
{AET.erase(AET.begin()+ii);}else{ii++;}}
//draw
{
bool flag=false;
for(int ii=0;ii!=AET.size();ii++){
if(flag)
fillline(i+min,(int)(AET[ii-1].x+0.5),(int)(AET[ii].x+0.5 ));
//if(flag)
std::cout<<i+min<<'\t'<<(int)(AET[ii].x+0.5)<<','<<(int)( AET[ii-1].x+0.5)<<'\n';
flag=!flag;
}}
for(int ii=0;ii!=AET.size();ii++){AET[ii]++;} }
delete[](ET);
}
void draw(){
drawgrid(0.8,0.8,0.8);
setcolor(1,0.5,0.5);
fill();
draweage(point,PN);
}
int main(int n,char*avg[]){
init(n,avg,"L2");
reinit(draw);
loop();
return0;
}
opengl.h
#include <GL/glut.h>
#define N 100
#define GRIDSIZE 5
int size=N*GRIDSIZE;
void init(int argc,char** argv,char*title){
//init openGL
size = N * GRIDSIZE;
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);
glutInitWindowPosition(10,10);
glutInitWindowSize(size, size);
glutCreateWindow(title);
glClearColor(1.0, 1.0, 1.0, 1.0);//white
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0,0.0,0.0);//black
gluOrtho2D(0, size,0, size);
}
void reinit(void(*p)()){
glutDisplayFunc(p);
}
void flush(){
glFlush();
}
void loop(){
glutMainLoop();
}
void clear(){
glClearColor(1.0, 1.0, 1.0, 1.0);//white
glClear(GL_COLOR_BUFFER_BIT);
}
void setcolor(double r,double g,double b){
glColor3f(r, g, b);
}
void drawline(int x1,int y1,int x2,int y2){
glBegin(GL_LINES);
glVertex2i(x1, y1);
glVertex2i(x2, y2);
glEnd();
flush();
}
void drawgrid(double r,double g,double b){
int i =0;
glColor3f(r, g, b);
for(i =0;i !=N *GRIDSIZE;i +=GRIDSIZE){drawline(i, 0, i, size);}
for(i =0;i !=N *GRIDSIZE;i +=GRIDSIZE){drawline(0, i, size, i);}
flush();
}
void drawpoint(int x,int y){
glPointSize((double)GRIDSIZE);
glBegin(GL_POINTS);
glVertex2i(x * GRIDSIZE, y * GRIDSIZE);
glEnd();
flush();
}
void draweage(int p[][2],int pn){
if(pn<2)return;
setcolor(0,0.8,0.8);
for(int i=0;i!=pn-1;i++){
drawline(p[i][0]*GRIDSIZE,p[i][1]*GRIDSIZE,p[i+1][0]*GRID SIZE,p[i+1][1]*GRIDSIZE);
}
drawline(p[pn-1][0]*GRIDSIZE,p[pn-1][1]*GRIDSIZE,p[0][0]* GRIDSIZE,p[0][1]*GRIDSIZE);
}
运行环境:ubuntu 13.10 + g++ 运行结果:。