康普顿散射公式

康普顿散射公式
康普顿散射公式是物理学中用于研究电磁波在某一物体表面上
反射或折射时，定义某种反射率或折射率的方程。

它是由美国物理学家Willard Harrison Cowperthwaite在1931年提出的，又被称为Cowperthwaite公式。

它的最大作用是可以用来预测某物体表面反射或折射的波的大小，也可以推断物体的表面属性。

康普顿散射公式的基本形式是：S=S0+S1(1-g)+S2(1+g)+S3，其中S为反射率或折射率，S0、S1、S2、S3为常数，g为微分系数。

该公式是根据反射或折射时光源和物体之间的位置和方向等条件来定
义的。

因为康普顿散射公式是一个多项式，在某种特定条件下，前4项可以认为是最重要的，所以可以简化为：S=S0+S1(1-g)+S2(1+g)。

康普顿散射公式计算的反射率或折射率会受到物体的表面属性
的影响，这就意味着，当物体的表面纹理凹凸不平时，其反射率会有所变化。

康普顿散射公式被广泛应用于多学科研究中，包括材料物理学、复合材料等。

它也被用于模拟某种物质表面反射或折射的光线，从而更好地了解物质的特性。

另外，康普顿散射公式也用于物理学的研究和机器视觉中，可以通过计算物体表面的反射率或折射率来模拟真实世界的物理现象，这有助于模拟特定的材料有关的参数和物理属性。

总之，康普顿散射公式是一个能够推断某物体表面反射或折射的
波的大小、推断物体表面属性以及模拟特定材料有关参数和物理属性的重要公式。

它已经在多学科研究中得到广泛应用，成为物理研究的重要工具。

由于论文中使用的散射光子数计算式是在仅考虑一次散射时得到的，我们下面计算了二次散射可能引起的修正。

附录A ：二次散射微分散射截面的推导
以下推导采用自然单位制。

康普顿散射的树图为：
由QED 二阶微扰得到的微分散射截面在电子静止参考系中的表达式为：
⎪⎭⎫
⎝⎛-+=Ωθωωωωωωασ
22222
sin '''2m d d 又有：ωωθ1'1)cos 1(1-=-m
代入得到： ⎪⎪⎭⎫ ⎝⎛+-++-+-=Ωθθωθωθωασ
2222
cos )cos 1()cos 1(]1/)cos 1([1
2m m m m m d d 在实验中，MeV m keV 511.0,20=≈ω
考虑二次散射：
则一个光子经过两次散射到达θ角的微分散射截面：
112112122
12112122
0)(cos ))cos(1())cos(1(]1/))cos(1('[12cos )cos 1()cos 1(]1/)cos 1([1
2ϕϕθϕθωϕθωϕθωαϕϕωϕωϕωασ
πd m m m m m m m m m m d d ⎪⎪⎭⎫ ⎝⎛-+--++--+--∙⎪⎪⎭⎫ ⎝⎛+-++-+-=Ω⎰由于式中含有222
)2(m α数量级的因子，而2
22
)2(m α<<1，因此二次散射引起的修正很小，可
以忽略高次散射，只计一次散射的结果。

康普顿效应散射公式推导过程在物理学的奇妙世界里，康普顿效应可是个相当有趣且重要的概念。

咱们今天就来好好唠唠康普顿效应散射公式的推导过程。

先来说说啥是康普顿效应。

想象一下，有一束 X 射线照到一块物质上，然后就发生了散射。

散射出来的 X 射线波长跟原来入射的波长不太一样，而且这个变化还跟散射角有关系。

这就挺神奇的，对吧？那咱们开始推导这个散射公式。

咱先假设入射的 X 射线光子能量是E = hν，动量是p = hν / c 。

这里的 h 是普朗克常量，ν 是频率，c 是真空中的光速。

当它和一个静止的自由电子发生碰撞时，根据动量守恒和能量守恒，就能得出一系列式子。

碰撞后，光子的能量变成了E' = hν' ，动量变成了p' = hν' / c 。

电子获得了一定的能量和动量。

设电子获得的能量是 E_e ，动量是p_e 。

根据动量守恒，在 X 方向上，有hν / c = hν' cosθ + p_e cosφ ；在 Y方向上，有0 = hν' sinθ - p_e sinφ 。

再结合能量守恒 E + m₀c² = E' + E_e 。

这里面 m₀是电子的静止质量。

经过一番复杂但有趣的数学运算和推导，最终就能得出康普顿效应的散射公式：Δλ = λ' - λ = (h / m₀c) (1 - cosθ)这就是康普顿效应散射公式啦！我还记得之前给学生们讲这个的时候，有个小家伙瞪着大眼睛，一脸迷茫地问我：“老师，这到底有啥用啊？”我笑着跟他说：“你想想啊，以后你要是去医院拍 X 光片，医生能通过这个原理更清楚地看到你的骨头有没有问题呢！”这孩子似懂非懂地点点头。

其实啊，康普顿效应的应用可不止在医学上。

在材料科学、天文学等领域都有着重要的作用。

通过对康普顿效应散射公式的推导和理解，我们能更深入地探索微观世界的奥秘，感受物理的魅力。

所以，同学们，可别小看了这个公式，它背后隐藏着无尽的知识和可能！希望大家能在物理的海洋里畅游，发现更多的精彩！。

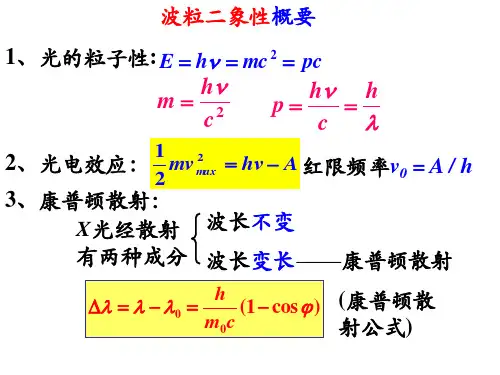
在康普顿效应中波长的改变量
在康普顿效应中，光的波长发生了改变。

康普顿效应描述了当X射线与物质相互作用时，光的波长如何改变。

康普顿效应可通过以下公式来表示:
Δλ = λ' - λ = λ_c * (1 - cosθ)
Δλ是波长改变量，λ'是散射后的波长，λ是入射光的波长，λ_c是康普顿波长，θ是散射角。

该公式表明，波长的改变量与康普顿波长以及散射角之间存在一定的关系。

需要注意的是，康普顿效应的波长改变量与入射光的波长无关，而是与散射角相关。

当散射角为0度时，波长改变量为0，即光的波长未发生改变。

随着散射角的增大，波长改变量也随之增大，表明光的波长发生了变化。

由于康普顿效应的波长改变量与散射角密切相关，在实际应用中可通过测量散射光的角度来确定波长的改变量。

这种方法在材料分析和X射线衍射等领域得到了广泛应用。

以上所述仅为康普顿效应中波长的改变量的一般表述，不包含具体实例。

康普顿散射康普顿（A. H. Compton ）的X 射线散射实验（康普顿散射）从实验上证实了光子是具有能量ωh =E 和动量k p h =的粒子，在微观的光子与电子的相互作用过程中，能量与动量守恒仍然成立。

康普顿散射实验在近代物理学发展史上起了重要作用，在研究核辐射粒子与物质的相互作用时发挥了重要的作用，在高能物理方面它至今仍是研究基本粒子结构及其相互作用的一个强有力的工具，并且为独立测定普朗克常数提供了一种方法。

1927年康普顿因发现X 射线被带电粒子散射而被授予诺贝尔物理学奖。

一 实验目的1. 学会康普顿散射效应的测量技术；2. 验证康普顿散射的γ光子能量及微分截面与散射角的关系。

二 实验原理1． 康普顿散射康普顿效应是射线与物质相互作用的三种效应之一。

康普顿效应是指入射光子与物质原子中的核外电子产生非弹性碰撞而被散射的过程。

碰撞时，入射光子把部分能量转移给电子，使它脱离原子成反冲电子，而散射光子的能量和运动方向发生变化。

如图1所示，其中hv 是入射γ光子的能量，v h ′是散射γ光子的能量，θ是散射光子的散射角，e 是反冲电子，φ是反冲电子的反冲角。

图1 康普顿散射示意图由于发生康普顿散射的γ光子能量比电子的束缚能要大的多，所以γ光子与原子中的电子相互作用时，可以把电子的束缚能忽略，看成是自由电子，并视为散射发生以前电子是静止的，动能为0，只有静止能量20c m 。

散射后，电子获得速度v ，此时电子的能量2201β−=c m E ，动量为201β−=v m mv ，其中cv=β，c 为光速。

由相对论的能量和动量守恒定律可以得到：v h c m hv c m ′+−=+220201β（1）φβθcos 1cos 20−+′=v m c v h c hv（2）θβθsin 1sin 20−=′v m c v h（3）由上三式可得出：)cos 1(120θ−+=′c m hvhvv h （4）其中c hv /是入射γ光子的动量，c v h /′是散射γ光子的动量，此式表示散射γ光子能量与入射γ光子能量及散射角的关系。

康普顿散射揭示光子与物质相互作用机制光子是光的基本单位，对于人类的了解和应用光线起着重要的作用。

然而，光子在与物质相互作用时会发生一系列复杂的现象，其中康普顿散射是一种重要的现象，它揭示了光子与物质相互作用的基本机制。

康普顿散射是指入射光子与物质中的自由电子相互作用后，光子能量发生改变并发生散射的过程。

这一过程的发现为粒子物理学和量子力学理论的发展做出了重要贡献。

康普顿散射的研究对于了解物质的结构、能量转化以及粒子之间的相互作用至关重要。

在康普顿散射过程中，光子与自由电子相互作用，光子被电子散射后的能量发生变化。

这个能量变化由康普顿散射公式描述：E' = E/(1 + (E/mc^2)(1 - cos(θ)))。

其中，E是入射光子的能量，E'是散射后光子的能量，m是电子的质量，c是光速，θ是散射角度。

根据这个公式，我们可以计算出散射后光子的能量与入射光子的能量之间的关系。

康普顿散射的发生是因为光子具有一定的粒子性质，而不仅仅是电磁波。

当光子与电子碰撞时，它们之间发生了能量的转移和动量的改变。

这个过程可以用相对论的动量守恒和能量守恒定律来解释：入射光子的能量转移到散射光子上，而散射角度的改变则与光子和电子的动量有关。

康普顿散射的研究不仅揭示了光子与物质相互作用的基本机制，也为量子力学理论的发展提供了重要的验证。

根据量子力学的波粒二象性理论，光子既可以看作是电磁波，也可以看作是光子粒子。

康普顿散射表明光子在与物质相互作用时表现出粒子性质，这对于量子力学的发展起到了积极的推动作用。

康普顿散射的研究对于现代科技的发展也有着重要的应用。

通过研究康普顿散射，科学家们可以了解物质的结构，验证量子力学的理论，改进医学成像技术等。

例如，康普顿散射在医学成像领域的应用已经成为一种无创、无辐射的影像技术，用于检测人体组织的构成和变化，从而实现早期疾病的发现和诊断。

除了医学应用外，康普顿散射还在核物理学、材料科学和宇宙学领域有着广泛的应用。

康普顿散射公式推导
康普顿散射公式是描述光子与物质相互作用的重要公式之一。

它是由美国物理学家康普顿于1923年提出的。

康普顿散射是指光子与物质中的自由电子相互作用后，光子的波长发生了变化。

这个过程可以用康普顿散射公式来计算。

康普顿散射公式为：λ'-λ= h/mc(1-cosθ)，其中λ和λ'分别为入射光子和散射光子的波长，h 为普朗克常数，m为电子质量，c为光速，θ为散射角度。

该公式表明，散射光子的波长与入射光子的波长之差取决于入射光子的能量和散射角度。

康普顿散射公式的推导是基于光子与自由电子的相互作用。

当光子入射到物质中时，它会与自由电子相互作用，使电子获得能量并发生运动。

在这个过程中，光子的能量和动量也会发生变化，从而导致光子的波长发生变化。

康普顿散射公式的重要性在于它可以用来研究物质的结构和性质，例如晶体结构、分子结构等。

康普顿散射还被应用于医学影像学中，用于测量人体内部组织的密度和成分。

康普顿散射公式是描述光子与物质相互作用的重要公式，它的推导基于光子与自由电子的相互作用。

该公式的应用范围广泛，对于研究物质的结构和性质以及医学影像学都具有重要意义。

约化普朗克常数乘以光速约化普朗克常数乘以光速，是量子力学中的一个重要参数，它也被称为康普顿波长。

康普顿波长的计算公式为h/(mc)，其中h是普朗克常数，m是粒子的质量，c是光速。

约化普朗克常数是普朗克常数除以2π，即h/(2π)，康普顿波长的公式也可以写成h/(mc)×2π。

约化普朗克常数乘以光速在量子力学中的应用非常广泛，特别是在计算原子和分子的能量和频率时。

下面我们分步骤来探讨一下约化普朗克常数乘以光速的应用。

第一步，计算康普顿波长。

康普顿波长是一个物体在粒子性和波动性之间转换所需要的波长。

例如，电子和光子在与物质相互作用的过程中，它们会发生一些散射现象，这个散射现象就可以用康普顿波长来计算。

康普顿波长越小，粒子的波动性越明显，越大则越接近于粒子性。

康普顿波长的计算公式即为h/(mc)×2π。

第二步，计算原子和分子的能量和频率。

原子和分子的能量和频率是量子力学的重要研究方向之一，也是实验物理的重点。

计算原子和分子的能量和频率需要使用Schrödinger方程，其中包含了约化普朗克常数乘以光速这个参数。

通过这个参数，我们可以更加准确地计算原子和分子的能量和频率。

第三步，研究康普顿效应。

康普顿效应是指X射线与物质相互作用的过程中产生的一种能量散射现象。

康普顿散射公式中也包含了约化普朗克常数乘以光速这个参数。

康普顿散射公式是X射线与物质相互作用的基本理论，也是现代物理学的重要研究方向之一。

综上所述，约化普朗克常数乘以光速在量子力学中的应用非常广泛。

通过对康普顿波长、原子和分子的能量和频率，以及康普顿效应的研究，我们可以深入了解物质的结构和性质。