第九章多元线性回归异方差问题

多元线性回归模型的异方差问题的浅析作者：尚云艳祝师强孙浩来源：《科技风》2022年第15期摘要：“应用回归分析”课程是高校应用统计学专业均开设的专业核心课程，多元线性回归模型是非常重要的知识内容，但是由于其理论内容复杂，学生学习难度大，针对此问题，本文从权的概念出发，利用权倒数的性质论证了加权线性回归的合理性。

并以北京市15个经济开发区的销售收入数据为例，运用加权最小二乘估计方法改进模型，最后从残差图和拟合值绝对误差（率）两个方面进行比较，结果均表明加权线性回归效果好。

该方法应用于教学，为教学内容的设计提供了新的思路，便于学生掌握并深入学习。

关键词：异方差;加权最小二乘估计;残差分析;权文献标识码：A回归分析的发展经历了很长的一段历史，早在18世纪，F.Galton提出利用最小二乘原理进行回归分析[1]，从那时开始，回归分析就越来越备受关注，但是随着回归分析的普及，在实际应用中往往出现违背线性回归假设的情况，比如，随机误差异方差、随机误差存在序列相关性、数据观测值异常等问题[2]。

特别是对随机误差异方差的情况，加权线性回归是对普通线性回归的一种改进，但是文献[3-4]中并未证明加权线性回归的合理性。

回归诊断是回归分析中必不可少的内容，由于回归假设都是针对随机误差项提出的，所以要从分析随机误差项ε的估计量（残差）入手，通过从残差和残差图分析来考察模型的合理性[5]。

本文主要讨论在随机误差异方差的情况下，怎样建立合理、合适的模型。

根据以往的经验，处理随机误差异方差问题的方法有加权最小二乘法（WLS）、BOX-COX变换法和方差稳定性变换法，这些方法应用于实际，可以消除或者减弱异方差对拟合模型造成的不良影响。

教科书上仅对加权线性回归的原理有所介绍，但是并没有涉及其本质内容。

本文通过权、权函数、权倒数的性质揭示了加权线性回归的本质，论证了其合理性。

以北京市经济开发区的销售收入数据为例，利用加权最小二乘法建立数学模型，并且进行比较分析，模拟结果表明加权线性回归比普通线性回归有一定的改进之处。

计量经济学实验报告多元线性回归、多重共线性、异方差实验报告一、研究目的和要求：随着经济的发展，人们生活水平的提高，旅游业已经成为中国社会新的经济增长点。

旅游产业是一个关联性很强的综合产业，一次完整的旅游活动包括吃、住、行、游、购、娱六大要素，旅游产业的发展可以直接或者间接推动第三产业、第二产业和第一产业的发展。

尤其是假日旅游，有力刺激了居民消费而拉动内需。

2012年，我国全年国内旅游人数达到亿人次，同比增长%，国内旅游收入万亿元，同比增长%。

旅游业的发展不仅对增加就业和扩大内需起到重要的推动作用，优化产业结构，而且可以增加国家外汇收入，促进国际收支平衡，加强国家、地区间的文化交流。

为了研究影响旅游景区收入增长的主要原因，分析旅游收入增长规律，需要建立计量经济模型。

影响旅游业发展的因素很多，但据分析主要因素可能有国内和国际两个方面，因此在进行旅游景区收入分析模型设定时，引入城镇居民可支配收入和旅游外汇收入为解释变量。

旅游业很大程度上受其产业本身的发展水平和从业人数影响，固定资产和从业人数体现了旅游产业发展规模的内在影响因素，因此引入旅游景区固定资产和旅游业从业人数作为解释变量。

因此选取我国31个省市地区的旅游业相关数据进行定量分析我国旅游业发展的影响因素。

二、模型设定根据以上的分析，建立以下模型Y=β0+β1X1+β2X2+β3X3+β4X4+Ut参数说明：Y ——旅游景区营业收入/万元X1——旅游业从业人员/人X2——旅游景区固定资产/万元X3——旅游外汇收入/万美元X4——城镇居民可支配收入/元收集到的数据如下（见表）：表 2011年全国旅游景区营业收入及相关数据（按地区分）数据来源：1.中国统计年鉴2012，2.中国旅游年鉴2012。

三、参数估计利用做多元线性回归分析步骤如下：1、创建工作文件双击图标，进入其主页。

在主菜单中依次点击“File\New\Workfile”，出现对话框“Workfile Range”。

多元线性回归模型检验引言多元线性回归是一种常用的统计分析方法，用于研究两个或多个自变量对目标变量的影响。

在应用多元线性回归前，我们需要确保所建立的模型符合一定的假设，并进行模型检验，以保证结果的可靠性和准确性。

本文将介绍多元线性回归模型的几个常见检验方法，并通过实例进行说明。

一、多元线性回归模型多元线性回归模型的一般形式可以表示为：$$Y = \\beta_0 + \\beta_1X_1 + \\beta_2X_2 + \\ldots + \\beta_pX_p +\\varepsilon$$其中，Y为目标变量，$X_1,X_2,\\ldots,X_p$为自变量，$\\beta_0,\\beta_1,\\beta_2,\\ldots,\\beta_p$为模型的回归系数，$\\varepsilon$为误差项。

多元线性回归模型的目标是通过调整回归系数，使得模型预测值和实际观测值之间的误差最小化。

二、多元线性回归模型检验在进行多元线性回归分析时，我们需要对所建立的模型进行检验，以验证假设是否成立。

常用的多元线性回归模型检验方法包括：1. 假设检验多元线性回归模型的假设包括：线性关系假设、误差项独立同分布假设、误差项方差齐性假设和误差项正态分布假设。

我们可以通过假设检验来验证这些假设的成立情况。

•线性关系假设检验：通过F检验或t检验对回归系数的显著性进行检验，以确定自变量与目标变量之间是否存在线性关系。

•误差项独立同分布假设检验：通过Durbin-Watson检验、Ljung-Box 检验等统计检验，判断误差项是否具有自相关性。

•误差项方差齐性假设检验：通过Cochrane-Orcutt检验、White检验等统计检验，判断误差项的方差是否齐性。

•误差项正态分布假设检验：通过残差的正态概率图和Shapiro-Wilk 检验等方法，检验误差项是否满足正态分布假设。

2. 多重共线性检验多重共线性是指在多元线性回归模型中，自变量之间存在高度相关性的情况。

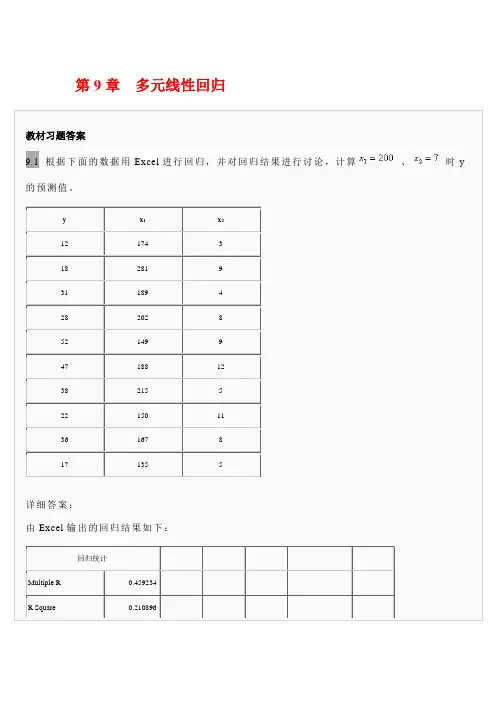
第9章多元线性回归教材习题答案9.1 根据下面的数据用Excel进行回归，并对回归结果进行讨论，计算、时y 的预测值。

y x1x212 174 318 281 931 189 428 202 852 149 947 188 1238 215 522 150 1136 167 817 135 5详细答案：由Excel输出的回归结果如下：回归统计Multiple R 0.459234R Square 0.210896Adjusted R Square -0.01456标准误差13.34122观测值10方差分析df SS MS F Significance F回归分析 2 332.9837 166.4919 0.93541 0.436485残差7 1245.916 177.988总计9 1578.9Coefficients 标准误差t Stat P-value Lower 95% Upper 95%Intercept 25.0287 22.27863 1.12344 0.298298 -27.6519 77.70928X Variable 1 -0.04971 0.105992 -0.46904 0.653301 -0.30035 0.200918X Variable 2 1.928169 1.47216 1.309755 0.231624 -1.55294 5.409276得到的回证方程为：。

表示，在不变的条件下，每变化一个单位，y平均下降0.04971个单位；表示，在不变的条件下，每变化一个单位，y平均增加1.928169个单位。

判定系数，表示在因变量y的变差中能够被y与和之间的线性关系所解释的比例为21.09%。

由于这一比例很低，表明回归方程的拟合程度很差。

估计标准误差，预测误差也较大。

方差分析表显示，Significance F=0.436485>a=0.05，表明y与和之间的线性关系不显著。

CFA 二级金融数量分析难点解析-多元回归异方差问题作者：高顿财经CFA助理讲师Kelly在多元回归假设中，其中有一项为残差的方差为常数，即残差的方差不随着自变量的变化而变化。

而异方差性（Heteroskedasticity）是指样本的残差在所有的观测数据中并不保持一致。

无条件的异方差性（unconditional heteroskedasticity）：虽然存在异方差，但是异方差性和自变量水平无关，即改变自变量的值不会对残差的方差产生影响。

如果一个回归中存在无条件的异方差性，回归结果也不会受到影响。

有条件的异方差性（unconditional heteroskedasticity）：异方差性和自变量水平相关，即残差的方差大小随着自变量的改变而改变。

可以用以下两个图形来形象地表示有条件的异方差性，图中的原点表示每一组的观测值，图中的直线表示运用OLS 方法估计的线性回归方程。

在左图中，实际观测值和估计的线性回归线之间的距离（即残差ε）随着自变量X的增大而增大，在右图中，实际观测值和估计的线性回归线之间的距离（即残差ε）随着自变量X的增大而减小。

异方差性对统计结果的影响：异方差性对统计结果的影响：1. 残差的估计是不可靠的。

2. 对回归系数（b）没有影响，OLS 的估计量仍然是无偏的，一致的。

3. 异方差性的存在会使得回归系数的标准差（S）高估（或者低估），从而使得t 统计量低估（或者高估），在决定是否拒绝原假设时会产生错误。

4. 异方差性会影响 F 统计值，使得F 检验失效。

异方差性检验方法：1. 观察残差的散点图：以自变量为X 轴，残差为Y 轴，将自变量和残差画在同一张坐标图中，然后观察残差是否随着自变量的变化而变化。

可以观察以下两图来区分异方差和同方差，在左图中残差与X 轴的距离不会随着自变量的变动而变动，为同方差，在右图中残差与X 轴的距离随着自变量的增大而增大，为异方差。

参与CFA考试的考生可按照复习计划有效进行，另外高顿网校官网考试辅导高清课程已经开通，还可索取CFA考试通关宝典，针对性地讲解、训练、答疑、模考，对学习过程进行全程跟踪、分析、指导，可以帮助考生全面提升备考效果。