2014年4月数量方法00994答案及真题
- 格式:pdf
- 大小:243.57 KB
- 文档页数:10

2014年10月数量方法二 (课程代码 00994) 参考答案附真题说明: 这里是最新2014年10月数量方法二试题的解答,为答谢购买和使用我们教材<<数量方法同步辅导与训练>>的朋友, 我们将继续第一时间同步更新更多有关的数量方法(课程代码00799,00994)的真题点评及答案,供购书的读者免费下载.请留意电子工业出版社的网页.未购书的其他读者也可免费浏览2014/12/29 作者一. 单选题1. A 参见<<数量方法同步辅导与训练>> 第11页自测题 (10)2. B 参见<<数量方法同步辅导与训练>> 第10页自测题 (6)3. D 参见<<数量方法同步辅导与训练>> 第14页 (2)---⑥4. C 参见<<数量方法同步辅导与训练>> 第16页 (4)---②5. B 参见<<数量方法同步辅导与训练>> 第16页(3)---③6. C 参见<<数量方法同步辅导与训练>> 第23页自测题 (11)7. A 参见<<数量方法同步辅导与训练>> 第29页 (8)---③8. D 参见<<数量方法同步辅导与训练>> 第29页 (8)---⑥9. D 参见<<数量方法同步辅导与训练>> 第29页 (8)---⑥10.题目是问计算估计标准误差的依据是什么?而估计标准误差是在回归分析中出现的,一元线性回归估计标准误差的计算公式为ys==多元线性回归估计标准差的计算公式为ys==其中k为自变元的个数. 这个ys的含义是回归模型中误差项的标准差的点估计(参见<<数量方法同步辅导与训练>>第61页(5). 而根据所给的四个选项,本题不是要考这个公式, 另外,还有一个标准误差的公式,即B yK Zh uS==,它是总体标准差σ的点估计. 综上,本题表述不清,题目题目似乎是想问:”计算抽样标准误差依据的是”,对这个问题的正确选项应该是C, 可参见<<数量方法同步辅导与训练>>第45页的例8.11.A 参见<<数量方法同步辅导与训练>>第38页的 (1)12.C 参见<<数量方法同步辅导与训练>>第46页的 (12)13.A 参见<<数量方法同步辅导与训练>>第42页的例2.14.A 参见<<数量方法同步辅导与训练>>第41页的4.15.D 参见<<数量方法同步辅导与训练>>第55页的例7.16.B 参见<<数量方法同步辅导与训练>>第60页的 1.17.B 参见<<数量方法同步辅导与训练>>第61页的 (5).18.B 参见<<数量方法同步辅导与训练>>第73页的 3.19.C 参见<<数量方法同步辅导与训练>>第91页的 (15)20.D 参见<<数量方法同步辅导与训练>>第92页的 (20).二. 填空题21.85.5 参见<<数量方法同步辅导与训练>>第7页的例2.22.2ˆD()bθ+参见<<数量方法同步辅导与训练>>第36页的知识点结构图.23.减小参见<<数量方法同步辅导与训练>>第57页的自测题(18).注:本题把显著性水平α改为犯第一类错误的概率更严谨.24.相关系数参见<<数量方法同步辅导与训练>>第60页的 1.25.12 参见<<数量方法同步辅导与训练>>第74页的 5.B yK Zh u三. 计算题26.组号 频数 频率 1 1 1/20 2 8 8/20 3 88/20 4 3 3/2027. 0.145 根据全概率公式,参见<<数量方法同步辅导与训练>>第21页的例928. 0.33199 根据随机变量的相关系数的公式计算:033199r .== 注: 我们教材中讲到的样本相关系数是上述随机变量相关系数的矩法估计29. (6.304, 6.696) 参见<<数量方法同步辅导与训练>>第41页的4.30. (1) 10573.%≈; 平均增长速度为5.73% (2) 350018629856 ()(%).+=亿元 参见<<数量方法同步辅导与训练>>第77页的例2. 31. (1) 总成本指数为: 65001060015200120001538554008500121507800.×+×+×=≈×+×+×;(2) 单位成本指数为: 65001060015200120001237155008600122009700.×+×+×=≈×+×+×参见<<数量方法同步辅导与训练>>第87页的例1.四. 应用题32. (1) 使用A,B 工艺的样本次品率分别为 6% 和10%; (2) 设A,B 工艺的产品次品率分别为12 p p 和, 原假设应为 012 H :p p ≥,备择假设应为112< H :p pBy K Zh u检验统计量为10454z .=≈−因 005.z z >−, 故接受原假设012 H :p p ≥,即不能认为使用工艺A 的产品次品率显著低于使用工艺B 的次品率.参见<<数量方法同步辅导与训练>>第55页的例6.33. (1) 相关系数r =0.9508; (2) 3783606007ˆy ..x =−+;(3) 估计标准差为1.1707.参见<<数量方法同步辅导与训练>>第63页的例2.附真题如下:ByK Zh uh uK ZB yh uK ZB yh uK ZB yh uK ZB y四. 应用题 (本大题共两题, 每小题10分,共20分)2014年10月数量方法二 (课程代码 00994) 参考答案 一. 单选题1. A 参见<<数量方法同步辅导与训练>> 第11页 自测题 (10)2. B 参见<<数量方法同步辅导与训练>> 第10页 自测题 (6)3. D 参见<<数量方法同步辅导与训练>> 第14页 (2)---⑥4. C 参见<<数量方法同步辅导与训练>> 第16页 (4)---②5. B 参见<<数量方法同步辅导与训练>> 第16页 (3)---③6. C 参见<<数量方法同步辅导与训练>> 第23页 自测题 (11)7. A 参见<<数量方法同步辅导与训练>> 第29页 (8)---③ByK Zh u。


2017年4月自考《数量方法二》真题及答案课程代码00994单项选择题:本大题共20小题,每小题2分,共40分。
在每小题列出的备选项中只有一项是最符合题目要求的,请将其选出。
1、某公司共有7个推销员,今年8月份这7个推销员的销售额分别为5500元、6500元、7300元、5300元、6000元、5500元、7200元,则这7个推销员销售额的中位数为()A.5500元B.6000元C.6460元D.6500元正确答案:B2、已知某班50名同学《大学英语》平均成绩是80分,该班30名男生的平均成绩是76分,则该班女生的平均成绩是()A.76分B.8C.85分D.86分正确答案:D3、将一枚硬币抛掷两次的样本空间Ω={00, 01, 10, 11}(用0表示出现正面,用1表示出现反面)。
则事件“第二次出现反面”可以表示为()A.{00,03}B.{10,01}C.{11,01}D.{10,11}正确答案:C4、盒子里装了2个红球和3个蓝球,从盒中任取两球,取到一个红球和一个蓝球的概率为A.3/5B.1/2C.6/25D.7/10正确答案:A5、设A、B、C为任意三个事件,则“在这三个事件中A与B同时发生且C 不发生”可以表示为()A.AB.BC.CD.D正确答案:D6、事件A、B相互对立,P(A)=0.3,, 则P(A+B)=()A.0B.0.3C.0.4D.1正确答案:D7、随机变量X的期望和方差分别表示X取值的()A.绝对值,离散程度B.平均值,平均程度C.平均值,离散程度D.相对值,平均程度正确答案:C8、已知随机变量X与Y有DX=5, DY=12,且COV(X,Y)=2.8,则D(X-Y-6)=()A.8.3B.11.4C.22.5D.26.8正确答案:B9、若已知DX=25,DY=9, COV(X,Y)=10.5,则X与Y相关系数r为()A.0.2B.0.6C.0.7D.0.8正确答案:C10、将总体单元在抽样之前按某种顺序排列,并按照设计的规则确定一个随机起点,然后每隔一定的时间隔逐个抽取样本单元的抽选方法称为()A.随机抽样B.分层抽样C.系统抽样D.分群抽样正确答案:C11、与样本均值的方差成反比的是()A.样本容量B.总体的方差C.总体的均值D.样本值正确答案:A12、在有限总体不重复抽样时,对于总体均值估计的样本量的确定,以下说法正确的是()A.样本量将随着允许误差的增加而减小B.样本量将随着置信水平提高而减小C.样本量不随允许误差的变化而变化D.样本量不随置信水平提高而变化正确答案:A13、某估计量是总体参数的一致性估计量,则以下说法错误的是()A.随着样本容量的增大,该估计量对总体参数真值的估计就愈精确B.随着样本容量的增大,该估计量会由有偏估计量变为无偏估计量C.可以通过增加样本容量来增加该估计量对总体参数真值估计的可靠性D.可以通过增加样本容量来提高该估计量对总体参数真值估计的可精度正确答案:B14、假设检验中,对总体的未知参数事件先作出的某种确定假设,通常称为()A.原假设B.备择假设C.对立假设D.以上全错正确答案:A15、显著性水平a表达了区间估计的()B.不可靠的概率C.准确性D.有效性正确答案:B16、如果相关系数|r|=1,则表明两个变量之间存在着()A.正相关B.不相关C.负相关D.完全相关正确答案:D17、若已知,n=100,则直线回归方程的回归系数为()A.0.27B.0.31C.0.42D.0.53正确答案:A18、这一公式适用于()A.时期数列计算序时平均数B.间隔相等的时点数列计算序时平均数C.间隔不相等的试点数列计算序时平均数D.由两个时点数列构成的相对数时间数列计算序时平均数B19、在指数体系中,总量指数与各因数指数之间的数量关系是()A.总量指数等于各因数指数之和B.总量指数等于各因数指数之差C.总量指数等于各因数指数之积D.总量指数等于各因数指数之商正确答案:C20、下列指数中,属于数量指标指数的有()A.农副产品产量总指数B.农副产品收购价格总指数C.某种工业产品成本总指数D.全部商品批发价格指数正确答案:A填空题(本大题共5小题,每小题2分,共10分)1、一组数据中最大值和最小值之差被称为_______。

2017年4月高等教育自学考试全国统一命题试卷数量方法(二) 试卷课程代码: 00994本试卷共5页,满分100分,考试时间150分钟。
考生答题注意事项:1. 本卷所有试卷必须在答题卡上作答。
答在试卷上的无效,试卷空白处和背面均可作草稿纸。
2. 第一部分为选择题。
必须对应试卷上的题号使用2B 铅笔将“答题卡”的相应代码涂黑。
3. 第二部分为非选择题。
必须注明大、小题号,使用0.5毫米黑色字迹签字笔作答。
4. 合理安排答题空间,超出答题区域无效。
第一部分 选择题一、单项选择题:本大题共20小题,每小题2分,共40分。
在每小题列出的备选项中只 有一项是最符合题目要求的,请将其选出。
1¥某公司共有7个推销员,今年8月份这7个推销员的销售额分别为5500元、6500元、7300元、5300元、6000元、5500元、7200元,则这7个推销员销售额的中位数为( ) A ¥5500元 B ¥6000元 C ¥6460元 D ¥6500元 答案:B解析:把所有的数按从小到大的顺序排列,6000正好是中间的那个数2¥已知某班50名同学《大学英语》平均成绩是80分,该班30名男生的平均成绩是76分,则该班女生的平均成绩是( )A ¥76分B ¥80分C ¥85分D ¥86分 答案:D 解析:(50×80-30×76)÷(50-30)= 3¥将一枚硬币抛掷两次的样本空间Ω={00, 01, 10, 11}(用0表示出现正面,用1表示出现 反面)。
则事件“第二次出现反面”可以表示为( )A ¥{00,03}B ¥{10,01}C ¥{11,01}D ¥{10,11} 答案:C解析:第二个数是1,第一个数可以是0也可以是14¥盒子里装了2个红球和3个蓝球,从盒中任取两球,取到一个红球和一个蓝球的概率为 A ¥ 3/5 B ¥1/2 C ¥6/25 D ¥7/10 答案:A解析:531032C C C 251312=⨯=5¥设A 、B 、C 为任意三个事件,则“在这三个事件中A 与B 同时发生且C 不发生”可以表示为( ) A ¥ABC B ¥C B A C ¥BC A D ¥C AB答案:D解析:AB 同时发生,所以AB 的上面没有横线,C 不发生,所以C 的上面有横线 6¥事件A 、B 相互对立,P(A)=0.3, P(B A )=0.7, 则P(A+B)=( ) A ¥ 0 B ¥0.3 C ¥0.4 D ¥1解析:7.0AB P -B P B A P ==)()()(,P (A+B )=P (A )+P(B)-P (AB )=0.3+0.7=1 7¥随机变量X 的期望和方差分别表示X 取值的( )A ¥绝对值,离散程度B ¥平均值,平均程度C ¥平均值,离散程度D ¥相对值,平均程度 答案:C解析:期望表示平均值,方差表示离散程度8¥已知随机变量X 与Y 有DX=5, DY=12,且COV(X,Y)=2.8,则D(X-Y-6)=( ) A ¥8.3 B ¥11.4 C ¥22.5 D ¥26.8 答案:B解析:D(X-Y-6)=DX+DY-2COV (X ,Y )=5+12-5.6=11.49¥若已知DX=25,DY=9, COV(X,Y)=10.5,则X 与Y 相关系数r 为( ) A ¥0.2 B ¥0.6 C ¥0.7 D ¥0.8 答案:C 解析:7.0355.10),(r =⨯==DYDX Y X COV 10¥将总体单元在抽样之前按某种顺序排列,并按照设计的规则确定一个随机起点,然后每隔一定的时间隔逐个抽取样本单元的抽选方法称为( )A ¥随机抽样B ¥分层抽样C ¥系统抽样D ¥分群抽样 答案:C解析:将总体单元在抽样之前按某种顺序排列,并按照设计的规则确定一个随机起点,然后每隔一定的时间隔逐个抽取样本单元的抽选方法称为系统抽样 11¥与样本均值的方差成反比的是( )A ¥样本容量B ¥总体的方差C ¥总体的均值D ¥样本值 答案:A解析:与样本均值的方差成反比的是样本容量12¥在有限总体不重复抽样时,对于总体均值估计的样本量的确定,以下说法正确的是( ) A ¥样本量将随着允许误差的增加而减小 B ¥样本量将随着置信水平提高而减小 C ¥样本量不随允许误差的变化而变化 D ¥样本量不随置信水平提高而变化 答案:A解析:在有限总体不重复抽样时,样本量将随着允许误差的增加而减小 13¥某估计量是总体参数的一致性估计量,则以下说法错误的是( ) A ¥随着样本容量的增大,该估计量对总体参数真值的估计就愈精确 B ¥随着样本容量的增大,该估计量会由有偏估计量变为无偏估计量 C ¥可以通过增加样本容量来增加该估计量对总体参数真值估计的可靠性 D ¥可以通过增加样本容量来提高该估计量对总体参数真值估计的可精度 答案:B解析:样本容量的增加,只会使估计量发生偏离,不会变为无偏估计14¥假设检验中,对总体的未知参数事件先作出的某种确定假设,通常称为( ) A ¥原假设 B ¥备择假设 C ¥对立假设 D ¥以上全错解析:对总体的未知参数事件先作出的某种确定假设叫原假设 15¥显著性水平a 表达了区间估计的( )A ¥可靠性B ¥不可靠的概率C ¥准确性D ¥有效性 答案:B解析:显著性水平a 表达了区间估计的不可靠的概率16¥如果相关系数|r|=1,则表明两个变量之间存在着( )A ¥正相关B ¥不相关C ¥负相关D ¥完全相关 答案:D解析:|r|=1表示完全相关 17¥若已知17322,11430,879,123912111====∑∑∑∑====ni i n i i i n i i ni ix y x y x,n=100,则直线回归方程的回归系数为( )A ¥0.27B ¥0.31C ¥0.42D ¥0.53 答案:A 解析:()27.022≈--=∑∑∑∑∑i ii i i i x x n y x y x n b18¥12 (2)321-++++=n a a a a a n这一公式适用于( ) A ¥时期数列计算序时平均数B ¥间隔相等的时点数列计算序时平均数C ¥间隔不相等的试点数列计算序时平均数D ¥由两个时点数列构成的相对数时间数列计算序时平均数 答案:B 解析:定义19¥在指数体系中,总量指数与各因数指数之间的数量关系是( ) A ¥总量指数等于各因数指数之和 B ¥总量指数等于各因数指数之差 C ¥总量指数等于各因数指数之积 D ¥总量指数等于各因数指数之商 答案:C 解析:在指数体系中,总量指数与各因数指数之间的数量关系是总量指数等于各因数指数之积20¥下列指数中,属于数量指标指数的有( ) A ¥农副产品产量总指数 B ¥农副产品收购价格总指数 C ¥某种工业产品成本总指数 D ¥全部商品批发价格指数 答案:A解析:数量指标反映物量变动水平。

2014年10月高等教育自学考试全国统一命题考试数量方法(二) 试卷(课程代码00994)本试卷共5页。
满分l00分,考试时间l50分钟。
考生答题注意事项:1.本卷所有试题必须在答题卡上作答。
答在试卷上无效,试卷空白处和背面均可作草稿纸。
2.第一部分为选择题。
必须对应试卷上的题号使用2B铅笔将“答题卡”的相应代码涂黑。
3.第二部分为非选择题。
必须注明大、小题号,使用0.5毫米黑色字迹签字笔作答。
4.合理安排答题空间,超出答题区域无效。
第一部分选择题一、单项选择题(本大题共20小题,每小题2分。
共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题卡”的相应代码涂黑。
未涂、错涂或多涂均无分。
1.某车间有2个生产小组负责生产某种零件,甲组有30名工人,乙组有20名工人。
在今年6月份,乙组平均每人生产80个零件,该车间50名工人平均每人生产74个零件,则甲组平均每人生产的零件数是A.70 B.74 C.75 D.802.某车间全体工人日产量的标准差是3,变异系数0.2,则平均产量为A.10 B.15 C.18 D.203.A与B相互对立,则A+B=A.空集 B.B C.A D.全集4.盒子里装了2个红球和3个蓝球,取出一个球后放回盒中再取下一个球。
第二次取出红球的概率为A.0.4 B.2 C.2.5 D.258.已知某批水果的坏果率服从正态分布N(0.04,0.09),则这批水果的坏果率的标准差为A.0.O4 B.O.O9 C.0.2 D.0.3A.1 B.2 C.3 D.410.计算估计标准误差的依据是A.总体的期望值 B.总体的方差 C.样本数据 D.样本的均值11.已知样本均值为,若将所有样本观察值都乘以,则新的样本均值为A.1 B.2 C.3 D.412.在保持样本容量和抽样方式不变的情况下,若要缩小置信区间,则置信度会A.变大 B.不变C.变小 D.可能变小也可能变大13.在大样本情况下,如果总体方差未知,利用正态分布构造的总体均值的置信区间为14.对方差已知的正态总体均值的假设检验,可采用的方法为A.Z检验 B.t检验 C.F检验 D.检验15.检验总体是否服从正态分布,可以采用的统计检验方法是A.t检验 B.Z检验 C.F检验 D.检验16.如果相关系数r=1,则表明两个变量之间存在着A.正相关 B.完全正相关 C.完全负相关 D.不相关17.与回归估计标准误差的计量单位相同的是A.自变量 B.因变量 C.相关系数 D.回归系数18.已知某时间数列各期的环比增长速度分别为ll%,l3%,l6%,该数列的定基发展速度为19.若价格持平,而贸易额增加,则贸易量指数A.下降 B.不变C.上升 D.不能确定20.同一数量货币,报告期只能购买基期商品量的90%,这是因为物价上涨A..l0% B.0 C.10% D.11.1%第二部分非选择题二、填空题(本大题共5小题,每小题2分,共l0分)请在答题卡上作答。
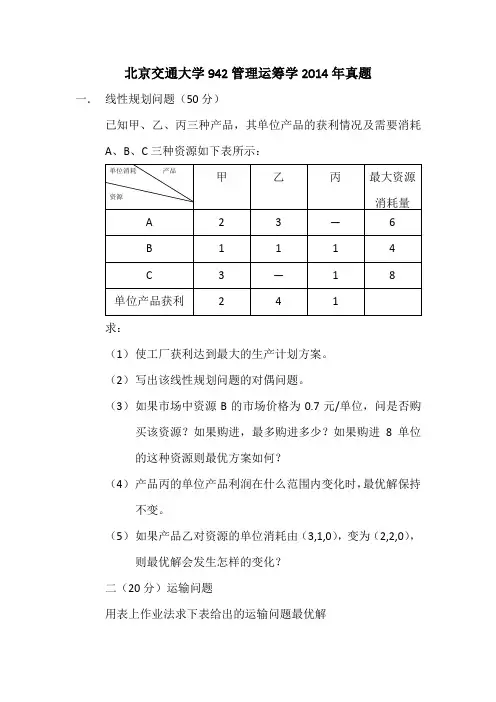
北京交通大学942管理运筹学2014年真题一.线性规划问题(50分)已知甲、乙、丙三种产品,其单位产品的获利情况及需要消耗A、B、C三种资源如下表所示:求:(1)使工厂获利达到最大的生产计划方案。
(2)写出该线性规划问题的对偶问题。
(3)如果市场中资源B的市场价格为0.7元/单位,问是否购买该资源?如果购进,最多购进多少?如果购进8单位的这种资源则最优方案如何?(4)产品丙的单位产品利润在什么范围内变化时,最优解保持不变。
(5)如果产品乙对资源的单位消耗由(3,1,0),变为(2,2,0),则最优解会发生怎样的变化?二(20分)运输问题用表上作业法求下表给出的运输问题最优解三(20分)用分支定界法求解整数规划模型: Max Z=3x 1+2x 2{2x 1+3x 2≤142x 1+x 2≤9x 1,x 2≥0且为整数四.动态规划问题(25分)某公司生产并销售某产品。
根据市场预测,今后四个月的市场需求量如下表所示。
已知生产一件产品的成本是1千元每批产品的生产准备成本是3千元,每月仅能生产一批,最多生产6件。
月末未售出的产品每件存储成本为0.5千元,且第一个月初无存货,第四个月末的存货要求为1,求最优生产计划五、求下图中各点间的最短路六.排队论(15分)在某单人理发店,顾客到达为普阿松流,平均到达间隔为15分钟,理发时间服从负指数分布,平均时间为10分钟。
求: (1) 顾客来理发必须等待的概率; (2) 理发店内顾客平均数;(3) 理发店内等待理发的顾客平均数; (4) 顾客在理发店平均等待理发的时间; (5) 店内恰有3个顾客的概率;91412122018121620v 5v 4v 2v 3v 15。

四. 应用题(本大题共两题, 每小题10分,共20分)
2014年10月数量方法二(课程代码 00994) 参考答案
(更多答案及点评内容请登陆数量方法同步辅导与训练的出版社链接)
一. 单选题
1. A 参见<<数量方法同步辅导与训练>> 第11页自测题 (10)
2. B 参见<<数量方法同步辅导与训练>> 第10页自测题 (6)
3. D 参见<<数量方法同步辅导与训练>> 第14页 (2)---⑥
4. C 参见<<数量方法同步辅导与训练>> 第16页 (4)---②
5. B 参见<<数量方法同步辅导与训练>> 第16页(3)---③
6. C 参见<<数量方法同步辅导与训练>> 第23页自测题 (11)
7. A 参见<<数量方法同步辅导与训练>> 第29页 (8)---③
8. D 参见<<数量方法同步辅导与训练>> 第29页 (8)---⑥。


全国2018年4月自学考试数量方法(二)试题课程代码:00994一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.一个试验中所有基本事件的全体所组成的集合称为()A.集合B.单元C.样本空间D.子集2.对于峰值偏向右边的单峰非对称直方图,一般来说()A.平均数>中位数>众数B.众数>中位数>平均数C.平均数>众数>中位数D.中位数>众数>平均数3.下列统计量中可能取负值的是()A.相关系数B.判定系数C.估计标准误差D.剩余平方和4.设A、B、C为任意三个事件,则“在这三个事件中A与B不发生但是C发生”可以表示为()A.A B C B.A B CC.AB C D.ABC5.样本估计量的分布称为()A.总体分布B.抽样分布C.子样分布D.经验分布6.估计量的一致性是指随着样本容量的增大,估计量()A.愈来愈接近总体参数值B.等于总体参数值C.小于总体参数值D.大于总体参数值7.原假设为假时,根据样本推断其为真的概率称为()A.显著性水平B.犯第一类错误的概率C.犯第二类错误的概率D.错误率8.一个实验的样本空间为Ω={1,2,3,4,5,6,7,8,9,10},A={1,2,3,4},B={2,3},C={2,4,6,8,10},则A B C=()A.{2,3} B.{2,4}12C .{4}D .{1,2,3,4,6,8}9.一个服从二项分布的随机变量,其方差与数字期望之比为3/4,则该分布的参数P 是( )A .1/4B .2/4C .3/4D .110.在一次抛硬币的试验中,小王连续抛了3次,则全部是正面向上的概率为( )A .91B .81C .61 D .3111.在一场篮球比赛中,A 队10名球员得分的方差是9,变异系数是0.2,则这10球员人均得分为( ) A .0.6 B .1.8 C .15D .2012.设A 、B 为两个事件,P (B )=0.7,P (B A )=0.3,则P (A +B )=( ) A .0.3 B .0.4 C .0.6D .0.713.已知某批水果的坏果率服从正态分布N (0.04,0.09),则这批水果的坏果率的标准差为( )A .0.04B .0.09C .0.2D .0.314.设总体X~N (μ,2σ),X 为该总体的样本均值,则( ) A .P (X <μ=<1/4 B .P (X <μ==1/4 C .P (X <μ=>1/2D .P (X <μ)=1/215.设总体X 服从正态分布N (μ,20σ),20σ已知,用来自该总体的简单随机样本X 1,X 2,…,X n 建立总体未知参数μ的置信水平为1-α的置信区间,以L 表示置信区间的长度,则( )A .α越大L 越小B .α越大L 越大C .α越小L 越小D .α与L 没有关系16.假设总体服从正态分布,在总体方差未知的情况下,检验H o :μ=0μ, H 1:μ>0μ的统计量为t =nS x /0μ-,其中n 为样本容量,S 为样本标准差,如果有简单随机样本X 1,X 2,…,X n ,与其相应的t <t a (n -1),则( ) A .肯定拒绝原假设B .肯定接受原假设C.有可能拒绝原假设D.有可能接受原假设17.一元回归直线拟合优劣的评价标准是()A.估计标准误差越小越好B.估计标准误差越大越好C.回归直线的斜率越小越好D.回归直线的斜率越大越好18.已知环比增长速度为2%、5%、6.1%,则定基增长速度为()A.2%×5%×6.1% B.(2%×5%×6.1%)-1C.102%×105%×106.1% D.(102%×105%×106.1%)-119.按照指数所反映的内容不同,指数可分为()A.个体指数和总指数B.简单指数和加权指数C.数量指标指数和质量指标指数D.动态指数和静态指数20表中a和b的数值应该为()A.125和120 B.120和80C.80和125 D.95和80二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。


精品自学考试资料推荐全国 2018年 4月高等教育自学考试数量方法(二)试题课程代码: 00994 第一部分选择题(共30分)一、单项选择题(本大题共 15小题,每小题 2 分,共 30分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.一组数据 3,4,5,5,6,7,8,9,10 中的中位数是()A . 5B . 5.5C. 6 D. 6.52.某企业 30 岁以下职工占 25%,月平均工资为 800 元; 30— 45 岁职工占 50%,月平均工资为 1000元; 45 岁以上职工占 25%,月平均工资 1100元,该企业全部职工的月平均工资为()A . 950 元B . 967 元C. 975 元D. 1000 元3.某一事件出现的概率为 1/4,试验 4 次,该事件出现的次数将是() A.1次B.大于1 次C .小于 1 次D .上述结果均有可能4.设 X、Y 为两个随机变量 D(X)=3 , Y=2X+3 ,则 D(Y)为()A .3 B.9C. 12 D. 155.某企业出厂产品 200 个装一盒,产品分为合格与不合格两类,合格率为99%,设每盒中的不合格产品数为 X ,则 X 通常服从()A .正态分布B .泊松分布C .均匀分布D .二项分布6.一个具有任意分布形式的总体,从中抽取容量为 n 的样本,随着样本容量的增大,样本均值 X 将逐渐趋向于()B.2分布A .泊松分布C.F 分布D.正态分布7.估计量的无偏性是指()A .估计量的数学期望等于总体参数的真值B .估计量的数学期望小于总体参数的真值C.估计量的方差小于总体参数的真值D.估计量的方差等于总体参数的真值8.显著性水平是指()A .原假设为假时,决策判定为假的概率B.原假设为假时,决策判定为真的概率C.原假设为真时,决策判定为假的概率D.原假设为真时,决策判定为真的概率 9.如果相关系数 r=- 1,则表明两个随机变量之间存在着()A .完全反方向变动关系B .完全同方向变动关系C .互不影响关系D .接近同方向变动关系10.当所有观察点都落在回归直线 y=a+bx 上,则 x 与 y 之间的相关系数为()A . r=0B . r2=1C. - 1<r<1 D. 0<r<111.某股票价格周一上涨 8%,周二上涨 6%,两天累计涨幅达()A .13%B .14%C. 14.5% D. 15%12.已知某地区2000 年的居民存款余额比1990 年增长了1 倍,比1995 年增长了0.5 倍, 1995 年的存款额比 1990 年增长了()A0.33 倍B0.5 倍C .0.75倍D.2倍13.说明回归方程拟合程度的统计量是()A .置信区间B.回归系数C .判定系数D.估计标准误差14.若采用有放回的等概率抽样,当样本容量为原来的9 倍,样本均值的标准误差将()A .为原来的1 B.为原来的19 3C .为原来的9倍D.不受影响15.设X和Y 为两个随机变量,D(X)=10,D(Y)=1 ,X与Y的协方差为 -3,则 D(2X -Y)为()A .18 B.24C38 D53第二部分非选择题(共70 分)三、填空题(本大题共 5 小题,每小题 2分,共 10分)请在每小题的空格中填上正确答案。
《数量方法(二)》(代码00994)自学考试复习提纲-附件1变异系数:表示数据相对于其平均数的分散程度。
%100⨯=xV σ⊙基本运算方法:1、一组数据3,4,5,5,6,7,8,9,10中的中位数是( ) A .5 B .5.5 C .6 D .6.5解析:按从小到大排列,此九个数中,正中间的是6,从而答案为C 。
2、某企业30岁以下职工占25%,月平均工资为800元;30—45岁职工占50%, 月平均工资为1000元;45岁以上职工占25%,月平均工资1100元,该企业全 部职工的月平均工资为( ) A .950元 B .967元 C .975元 D .1000元解析:25%*800+50%*1000+25%*1100=975,故选C 。
3、有一组数据的平均数和标准差分别为50、25,这组数据的变异系数为( ) A.0.2 B.0.4 C.0.5D.0.7解析:变异系数%100⨯=xV σ=250.550=,故选C 。
4、若两组数据的平均值相差较大,比较它们的离散程度应采用( ) A .极差 B .变异系数 C .方差 D .标准差 解析:考变异系数的用法,先B 。
5、一组数据4,4,5,5,6,6,7,7,7,9,10中的众数是( ) A .6 B .6.5 C .7D .7.5解析:出现最多的数为众数,故选C 。
6、对于峰值偏向左边的单峰非对称直方图,一般来说( ) A .平均数>中位数>众数 B .众数>中位数>平均数 C .平均数>众数>中位数 D .中位数>众数>平均数 解析:数据分布是对称分部时: 众数=中位数=平均数数据分布不是对称分部时:左偏分布时:众数<中位数<平均数右偏分布时:众数>中位数>平均数需要记住提,峰值偏向左边的单峰非对称直方图称为右偏分布,峰值偏向右边的单峰非对称直方图称为左偏分布,从而此题答案为B 。
第二章 随机事件及其概率⊙基本知识点:一、 随机试验与随机事件:1. 随机试验:a) 可以在相同的条件下重复进行;b) 每次试验的可能结果可能不止一个,但是试验的所有可能的结果在试验之前是确切知道的;c) 试验结束之前,不能确定该次试验的确切结果。
全国2010年4月高等教育自学考试数量方法(二)试题课程代码:00994一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.有一组数据99,97,98,101,100,98,100,它们的平均数是( ) A.98 B.98.5C.99 D.99.22.一组数据中最大值与最小值之差,称为( )A.方差B.标准差C.全距D.离差3.袋中有红、黄、蓝球各一个,每一次从袋中任取一球,看过颜色后再放回袋中,共取球三次,颜色全相同的概率为( )A.1/9 B.1/3C.5/9 D.8/94.设A、B、C为任意三事件,事件A、B、C至少有一个发生被表示为( ) A.A B.C.D.A+B+C5.掷一枚骰子,观察出现的点数,记事件A={1,3,5},B={4,5,6},C={1,6}则C—A=( )A.{3,5,6} B.{3,5}C.{1} D.{6}6.已知100个产品中有2个废品,采用放回随机抽样,连续两次,两次都抽中废品的概率为( )A.B.C. D.7.随机变量X服从一般正态分布N(),则随着的减小,概率P(|X—|<)将会( )A.增加B.减少C.不变D.增减不定8.随机变量的取值一定是( )A.整数B.实数C.正数D.非负数9.服从正态分布的随机变量X的可能取值为( )A.负数B.任意数C.正数D.整数10.设X1,……Xn为取自总体N()的样本,和S2分别为样本均值和样本方差,则统计量服从的分布为( )A.N(0,1) B.(n-1)C.F(1,n-1) D.t(n-1)11.将总体单元在抽样之前按某种顺序排列,并按照设计的规则确定一个随机起点,然后每隔一定的间隔逐个抽取样本单元的抽选方法被称为( )A.系统抽样B.随机抽样C.分层抽样 D.整群抽样12.估计量的无偏性是指估计量抽样分布的数学期望等于总体的( ) A.样本 B.总量C.参数D.误差13.总体比例P的90%置信区间的意义是( )A.这个区间平均含总体90%的值B.这个区间有90%的机会含P的真值C.这个区间平均含样本90%的值D.这个区间有90%的机会含样本比例值14.在假设检验中,记H0为待检验假设,则犯第二类错误是指( ) A.H0真,接受H0 B.H0不真,拒绝H0C.H0真,拒绝H0 D.H0不真,接受H015.对正态总体N(,9)中的进行检验时,采用的统计量是( ) A.t统计量B.Z统计量C.F统计量D.统计量16.用相关系数来研究两个变量之间的紧密程度时,应当先进行( ) A.定量分析 B.定性分析C.回归分析D.相关分析17.若变量Y与变量X有关系式Y=3X+2,则Y与X的相关系数等于( ) A.一1 B.0C.1 D.318.时间数列的最基本表现形式是( )A.时点数列B.绝对数时间数列C.相对数时间数列D.平均数时间数列19.指数是一种反映现象变动的( )A.相对数B.绝对数C.平均数D.抽样数20.某公司2007年与2006年相比,各种商品出厂价格综合指数为110%,这说明( )A.由于价格提高使销售量上涨10% B.由于价格提高使销售量下降10%C.商品销量平均上涨了10%D.商品价格平均上涨了10%二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
《数量方法(二)》自学考试复习题目(按照章节题型归类)第一章数据的整理和描述一、选择题一般用来描述和表现各成分占全体的百分比的图形是()A.条形图B.饼形图C.柱形图D.百分比图有一组数据99,97,98,101,100,98,100,它们的平均数是( ) A.98 B.?C.99 D.一组数据中最大值与最小值之差,称为( )A.方差B.标准差C.全距D.离差一个数列的平均数是8,变异系数是,则该数列的标准差是( )A. 2一般用来表现两个变量之间相互关系的图形是( )`A.柱形图B.饼形图C.散点图D.曲线图对极端值最敏感的度量集中趋势的指标是()A.中位数B.众数C.标准差D.平均数某公司共有5名推销员。
在今年8月份这5名推销员的平均销售额为6600元,其中有3名推销员的平均销售额为7000元,则另外2名销售员的平均销售额为();8-某车间有2个生产小组负责生产某种零件,甲组有30名工人,乙组有20名工人。
在今年6月份,甲组平均每人生产70个零件,乙组平均每人生产80个零件。
则该车间50名工人在今年6月份平均每人生产的零件数是( )9-已知某班50名同学《数量方法》考试平均成绩是80分,该班20名男生的平均成绩是86分,则该班女生的平均成绩是( )个工人生产的零件数分别为53、48、65、50、59,则这5个数字的中位数是()A.48 B.53,C.59 D.65一个数列的方差是4,变异系数是,则该数列的平均数是()A.B.C.10 D.20. 1.某公司上半年6个月的利润分别为80、85、75、70、82、78(单位:万元),则上半年的月平均利润为( )A. 78 B.C.79 D. 80一个数列的平均数是8,变异系数是,则该数列的方差是( )-B.4C.16 D.32. 1.一个由7个工人组成的生产小组负责生产某种零件。
今年6月份这7个工人生产的零件数分别为53、48、53、65、50、53、59,则这7个工人生产零件数的众数是()A.48 B.53C.59 D.65已知某班50名同学《大学英语》考试平均成绩是80分,该班30名男生的平均成绩是76分,则该班女生的平均成绩是()A.76分B.80分C.85分D.86分(在一次《数量方法》考试中,某班平均成绩是80分,标准差是4分,则该班考试成绩的变异系数是()A.B.0.2 C.5 D.20对于峰值偏向右边的单峰非对称直方图,一般来说()A.平均数>中位数>众数B.平均数<中位数<众数C.平均数>众数>中位数D.平均数< 众数<中位数某车间有2个生产小组负责生产某种零件,甲组有30名工人,乙组有20名工人,在今年6月份,乙组平均每人生产80个零件,该车间50名工人平均每人生产74个零件,则甲组平均每人生产零件数是()A.70 B.74 C.75 D.80某车间全体工人日产量的标准差是3,变异系数为,则平均产量为()@A.10 B.15 C.18 D.20答案:二、填空题按照被描述的对象与时间的关系,数据可以分为时间序列数据、平行数据和.若一组数据的平均值为5,方差为9,则该组数据的变异系数为。