湖南省蓝山县第一中学九年级数学上册 第二章 第3课时 解一元二次方程配方法教案 新版湘教版教案

2.2一元二次方程的解法 配方法学习目标1复习巩固配方法解二次项系数为1的一元二次方程；2.掌握用配方法解二次项系数不是1的一元二次方程;3.体会转化的数学思想．学习重点：用配方法解二次项系数不是1的一元二次方程；学习难点：熟练掌握用配方法解一元二次方程；一、温故知新：1、填空2、用配方法解一元二次方程比较方程x 2-4x-6=0与方程2x 2-4x-6=0思考：1、有什么不同？2、能用配方法解吗？解法与上题一样吗？你解得出吗？3、怎么把它变成我们会解的那种？二．自主学习：【任务一】大胆尝试解方程：2x 2-4x-6=0要求：1、先大胆尝试，独立探究；2、感觉困难的，可自学P14页的【例8】；3、能独立尝试出来的，有了结果后，打开教材例8，对照教材的完整过程，找到自己的不足和疑惑；4、记录自己的疑惑，以备小组讨论；【互动】：1、 小组讨论，记录疑惑；2、 请学生上黑板板书；3、 请学生点评；【目标】1、 使学生掌握二次项系数不是1的一元二次方程如何解；2、 通过学生出现的一些错误来点拨易错或需注意的地方；3、 让学生理解为什么要除以2？为什么能除以2？依据是什么？【任务二】试解方程：2x 2-5x+3=0【目标】1、 巩固任务一所掌握的方法；2、 二次项系数化为1后，一次项系数不是一个整数时，应该怎么办？三、检测222222(1)8989()(2)11()x x x x x x x x x x --=-+--=--+-=++--=+-2460x x --=用配方法解下列方程【目标】1、 通过练习巩固配方法解方程；2、 不是一般形式的一元二次方程怎么解；3、 让学生总结：用配方法解一元二次方程的一般步骤；【任务三】下列一元二次方程用什么方法解更简单？【目标】1、 把握每一种解法所对应的方程特点；2、 小结出解一元二次方程的算法；（阅读教材P15）五、作业教材P19 习题1.2A 组第3题反思：1、任何一道题目的设计都能围绕本节课的重点和难点；2、充分让学生暴露问题，同时让学生来解决；3、本节课的开放与生成还可以，学生提出的问题比较多，且具有一定的探讨价值。

2．2一元二次方程的解法2．2.1配方法教课目的【知识与技术】1．知道解一元二次方程的基本思路是“降次”化一元二次方程为一元一次方程．2．学会用直接开平方法解形如(ax＋b)2－k＝0(k ≥的0)方程．3．理解“配方”是一种常用的数学方法，在用配方法将一元二次方程变形的过程中，让学生进一步领会化归的思想方法．【过程与方法】经过研究配方法的过程，让学生领会转变的数学思想方法．【感情态度】学生在独立思虑和合作研究中感觉成功的愉悦，并体验数学的价值，增强学生学习数学的兴趣．【教课要点】运用配方法解一元二次方程．【教课难点】把一元二次方程转变为形如(x＋ n)2＝ d(d ≥的0)过程．教课过程一、情形导入，初步认知1．依据完整平方公式填空：(1)x2＋ 6x＋9＝()2(2)x2－ 8x＋16＝()2(3)x2＋ 10x＋()2＝()2(4)x2－ 3x＋()2＝()22．前方我们已经学了一元一次方程和二元一次方程组的解法，解二元一次方程组的基本思路是什么？(消元、化二元一次方程组为一元一次方程)．由解二元一次方程组的基本思路，你能想出解一元二次方程的基本思路吗？3．你会解方程x2＋6x－ 16＝0 吗？你会将它变为 (x＋m)2＝ n(n 为非负数 )的形式吗？试一试看．假如是方程2x2＋1＝3x 呢？【教课说明】学会利用完整平方知识填空，初步配方为后边学习打下基础．二、思虑研究，获得新知1．解方程： x2－2500＝0.问：如何将这个方程“降次”为一元一次方程？把方程写成 x2＝2500这表示 x 是 2500 的平方根，依据平方根的意义，得x＝2500或 x ＝－2500所以，原方程的解为x1＝50， x2＝－ 50【概括结论】一元二次方程的解也是一元二次方程的根．[ 根源 :学 * 科 * 网Z*X*X*K]2．解方程 (2x＋ 1)2＝2解：依据平方根的意义，得2x＋1＝2或 2x ＋1＝－2所以，原方程的根为x1＝2－1，x2＝－2＋ 1 223．经过上边的两个例题，你知道什么时候用开平方的方法来解一元二次方程呢？【概括结论】对于形如 (x＋n)2＝d(d ≥的0)方程，可直接用开平方法解．直接开平方法的步骤是：把方程变形成(x＋n)2＝ d(d ≥，0)而后直接开平方得x＋n＝和 x＋ n＝－，分别解这两个一元一次方程，获得的解就是原一元二次方程的解．4．解方程 x2＋4x＝12我们已知，假如把方程x2＋4x＝12 写成 (x＋ n)2＝ d 的形式，那么就能够依据平方根的意义来求解．那么，如何将左侧写成 (x＋n)2的形式呢？我们学过完整平方式，你可否将左侧x2＋4x 添上一项使它成为一个完整平方式．请互相沟通．写出解题过程．【概括结论】一般地，像上边这样，在方程x2＋4x＝ 12 的左侧加前一次项系数的一半的平方，在减去这个数，使得含未知数的项在一个完整平方式里，这类做法叫作配方．配方、整理后就能够直接依据平方根的意义来求解了．这类解一元二次方程的方法叫作配方法．5．如何用配方法解方程25x2＋50x－ 11＝0 呢？假如二次项系数为1，那就好办了！那么如何将二次项的系数化为 1 呢？同伴之间能够互相沟通．试着写出解题过程．6．经过上边配方法解一元二次方程的过程，你能总结用配方法解一元二次方程的步骤吗？【概括结论】用配方法解一元二次方程的步骤：(1)把方程化为一般形式ax2＋bx＋c＝0；(2)把方程的常数项经过移项移到方程的右侧；(3)若方程的二次项系数不为 1 时，方程两边同时除以二次项系数a；(4)方程两边同时加前一次项系数一半的平方；(5)此时方程的左侧是一个完整平方式，而后利用平方根的定义把一元二次方程化为两个一元一次方程来解．【教课说明】经过这一过程，学生发现能用直接开平方法求解的方程都能够转变为一般形式，一般形式的方程也能用配方法转变为能够直接开平方的形式，所以总结出解一元二次方程的基本思路是将一元二次方程转变为(x＋n)2＝d(d ≥ 0)的形式．三、运用新知，深入理解1．赐教材 P33 例 3、P34 例 4.2．列方程 (注：学生练习，教师巡视，适合指导．)(1)x2－ 10x＋24＝0；(2)(2x－1)(x＋ 3)＝5；(3)3x2－6x＋4＝0.解： (1)移项，得 x 2－10x＝－ 24配方，得 x2－ 10x＋25＝－ 24＋25，由此可得 (x－5)2＝1，x－ 5＝±1，∴x1＝6，x2＝ 4.(2)整理，得 2x2＋5x－8＝0.移项，得 2x2＋5x＝825二次项系数化为 1 得 x ＋2x ＝4，555配方，得 x2＋ x ＋( )2＝ 4＋( )22445 289(x＋4)＝16，589由此可得 x ＋4＝±4，x＝－5＋ 89，x ＝－5－ 89. 1424(3)移项，得 3x2－6x＝－ 4二次项系数化为 1，得 x2－2x＝－4 3，配方，得 x2－ 2x＋12＝－43＋12，(x－1)2＝－1 3由于实数的平方不会是负数，所以x 取任何实数时， (x－1)2都是非负数，上式都不建立，即原方程无实数根．3．解方程 x2－8x＋1＝0剖析：明显这个方程的左侧不是一个完整平方式，所以，要按前方的方法化为完整平方式．解： x2－ 8x＋1＝0移项得： x2－8x＝－ 1配方得： x2－8x＋16＝－ 1＋16即(x－4)2＝15两边开平方得： x － 4＝ ± 15∴ x 1＝4＋ 15，x 2＝4－ 15.4．用配方法将以下各式化为 a(x ＋h)2 ＋k 的形式．22 21 (1)－3x － 6x ＋1；(2)y ＋ y ＋2；33(3)0.4x 2－0.8x －1.解： (1)－3x 2－6x ＋121＝－ 3(x ＋ 2x －3)22 21＝－ 3(x ＋ 2x ＋1 － 1 －3)24＝－ 3[(x ＋ 1) － 3]＝－ 3(x ＋1)2＋42 2 1 (2)3y ＋3y －22 21＝3(y ＋2y －3)2211 1 2－3]＝3[y ＋ 2y ＋(4)2－ (4) 212 49 ＝3[(y ＋4) －16]2 12 49 ＝3(y ＋4) －24.(3)0.4x 2 －0.8x －1＝ 0.4(x 2－2x －2.5)＝ 0.4[(x 2－2x ＋ 12)－12－ 2.5]＝ 0.4(x －1)2 －1.4【教课说明】经过练习，使学生能灵巧运用“配方法 ”，并增强学生对一元二次方程解的认识．四、师生互动、讲堂小结先小组内沟通收获和感想，尔后以小组为单位派代表进行总结．教师作以补充．课后作业部署作业：教材“习题 2.2 ”中第 1、2、3 题．教课反省在教课过程中，坚持由简单到复杂，由特别到一般的原则，采纳了察看对照，合作研究等不一样的学习方式，充足发挥学生的主体作用，让学生主动研究发现结论，教师做学生学习的指引者，合作者，促使者，要合时鼓舞学生，实现师生互动．同时，我认识到教师不只是要教给学生知识，更要在教课中浸透数学中的思想方法，培育学生优秀的数学修养和学习能力，让学生学会学习．2．2.2公式法教课目的【知识与技术】1．经历推导求根公式的过程，增强推理技术的训练．2．会用公式法解简单系数的一元二次方程．【过程与方法】经过由配方法推导求根公式，培育学生推理能力和由特别到一般的数学思想．【感情态度】让学生体验到全部一元二次方程都能运用公式法去解，形成全面解决问题的踊跃感情，感觉公式的对称美、简短美，产生热爱数学的感情．【教课要点】求根公式的推导和公式法的应用．【教课难点】理解求根公式的推导过程．教课过程一、情形导入，初步认知1．用配方法解方程：(1)x 2＋ 3x ＋2＝0；(2)2x 2－ 3x ＋5＝0.2．由用配方法解一元二次方程的基本步骤知： 对于每个详细的一元二次方程，都使用了同样的一些计算步骤，这启迪我们思虑，能不可以对一般形式的一元二次方程 ax 2＋bx ＋ c ＝ 0(a ≠使0)用这些步骤，而后求出解x 的公式？【教课说明】这样做了此后，我们能够运用这个公式来求每一个详细的一元二次方程的解，获得一通百通的成效．二、思虑研究，获得新知1．用配方法解方程： ax 2＋bx ＋ c ＝ 0(a ≠ 0)剖析：前方详细数字已做了好多，我们此刻不如把a 、b 、c 也当作一个详细数字，依据上边的解题步骤就能够向来推下去．解：移项，得： ax 2＋bx ＝－ c由于 a ≠0，所以方程两边同除以 a 得：b cx 2＋ x ＝－aa2bb 2c b2配方，得： x ＋ x ＋() ＝－＋( )a 2a a2a即(x ＋ b)2＝b 2－4ac2a 4a 2∵a ≠0，∴ 4a 2>0b2－ 4ac当 b2－ 4ac ≥0，4a2≥0b b2－ 4ac∴x＋2a＝±2a－b± b2－4ac即 x ＝2a－b＋ b2－4ac∴x1＝2a，－b－ b2－4acx2＝2a.当 b2－ 4ac<0时，方程无解．【概括结论】由上可知，一元二次方程ax2＋ bx＋c＝0(a ≠的0)根由方程的系数 a、 b、c 而定，所以：(1)解一元二次方程时，能够先将方程化为一般形式ax2＋bx＋c＝ 0，当 b2－4ac≥0时，将 a、 b、 c 代入式子x＝－b± b2－4ac 22a(b － 4ac ≥ 0)便可求出方程的根．(2)这个式子叫做一元二次方程的求根公式．(3)利用求根公式解一元二次方程的方法叫公式法．【重申】用公式法解一元二次方程时，一定注意两点：(1)将 a、b、c 的值代入公式时，必定要注意符号不可以犯错． (2)式子 b2－4ac ≥0是公式的一部分．【教课说明】让学生思虑对于一般形式的一元二次方程ax2＋bx＋ c＝0(a ≠ 0)可否用配方法求出它的解？经过解方程发现概括一元二次方程的求根公式．2．展现课本 P36 例 5(1)，(2)，按课本方式指引学生用公式法解一元二次方程，并提示学生在确立a，b，c 的值时，先要将一元二次方程式化为一般形式，注意 a，b， c 的符号．3．指引学生达成P37 例 6.4．你能总结出用公式法解一元二次方程的一般步骤吗？【概括结论】第一要把原方程化为一般形式，进而正确地确立a，b，c 的值；其次要计算 b2－4ac 的值，当 b2－4ac ≥0时，再用求根公式求解．三、运用新知，深入理解1．用公式法解以下方程．2x2＋ 3＝ 7x剖析：用公式法解一元二次方程，需先确立a、b、c 的值、再算出 b2－4ac．．的值、最后辈入求根公式求解．解：2x2－7x＋3＝0．a＝ 2， b＝－ 7， c＝ 3∵b2－4ac＝ (－7)2－4×2×3＝25>0∴x＝－b± b2－4ac7± 257±5 2a＝2×2＝41即 x1＝ 3，x2＝2.2．某数学兴趣小组对对于x 的方程 (m＋1)xm2＋1＋(m－ 2)x－ 1＝ 0 提出了下列问题．(1)若使方程为一元二次方程，m 能否存在？若存在，求出m 并解此方程．(2)若使方程为一元一次方程m 能否存在？若存在，恳求出．[ 根源 :1ZXXK]你能解决这个问题吗？剖析： (1)要使它为一元二次方程，一定知足m2＋1＝2，同时还要知足 (m＋1) ≠0.(2)要使它为一元一次方程，一定知足∶①m2＋1＝1m2＋ 1＝ 0或②或（m＋1）＋（ m－2）≠0m－≠02m＋1＝0③m－2≠0解： (1)存在．依据题意，得： m2＋ 1＝ 2m2＝1m＝±1当 m＝ 1 时， m＋ 1＝ 1＋1＝2≠0[根源 :学。

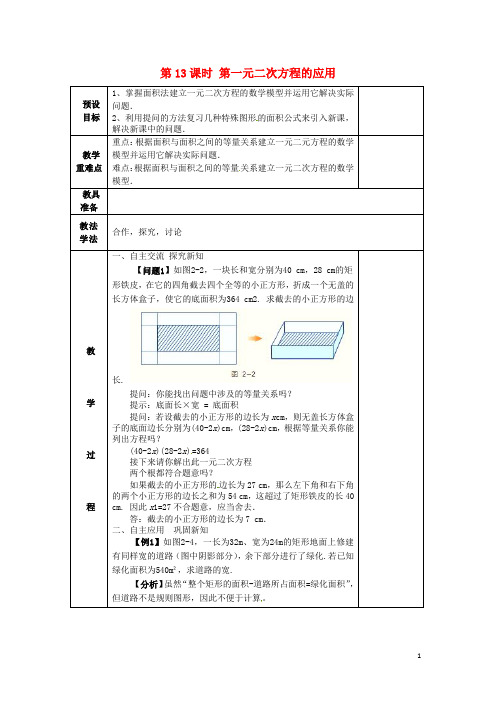
第13课时第一元二次方程的应用预设目标1、掌握面积法建立一元二次方程的数学模型并运用它解决实际问题．2、利用提问的方法复习几种特殊图形的面积公式来引入新课，解决新课中的问题．教学重难点重点：根据面积与面积之间的等量关系建立一元二元方程的数学模型并运用它解决实际问题．难点：根据面积与面积之间的等量关系建立一元二次方程的数学模型．教具准备教法学法合作，探究，讨论教学过程一、自主交流探究新知【问题1】如图2-2，一块长和宽分别为40 cm，28 cm的矩形铁皮，在它的四角截去四个全等的小正方形，折成一个无盖的长方体盒子，使它的底面积为364 cm2. 求截去的小正方形的边长.提问：你能找出问题中涉及的等量关系吗？提示：底面长×宽 = 底面积提问：若设截去的小正方形的边长为x cm，则无盖长方体盒子的底面边长分别为(40-2x)cm，(28-2x)cm，根据等量关系你能列出方程吗？(40-2x)(28-2x)=364接下来请你解出此一元二次方程两个根都符合题意吗？如果截去的小正方形的边长为27 cm，那么左下角和右下角的两个小正方形的边长之和为54 cm，这超过了矩形铁皮的长40 cm. 因此x1=27不合题意，应当舍去．答：截去的小正方形的边长为7 cm．二、自主应用巩固新知【例1】如图2-4，一长为32m、宽为24m的矩形地面上修建有同样宽的道路（图中阴影部分），余下部分进行了绿化.若已知绿化面积为540m²，求道路的宽.【分析】虽然“整个矩形的面积-道路所占面积=绿化面积”，但道路不是规则图形，因此不便于计算。

【例2】如图2-6所示，在△ABC中，∠C=90°， AC=6cm，BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动；同时点Q沿CB边从点C向终点B以2cm/s的速度移动，且当其中一点到达终点时，另一点也随之停止移动.问点P，Q出发几秒后可使△PCQ的面积为9cm²？问题中涉及的等量关系是什么？你能根据等量关系列出方程吗？三自主总结拓展新知本节课应掌握：利用已学的特殊图形的面积公式建立一元二次方程的数学模型并运用它解决实际问题．四、当堂练习教材P52练习题1、2题。