2018届山东省实验中学高三第三次模拟考试(打靶题)理科数学试题及答案 精品

2018年普通高考模拟考试理科数学2018.5本试卷共5页，23题(含选考题)．全卷满分150分．考试用时120分钟．★祝考试顺利★注意事项：1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置．2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．写在试卷、草稿纸和答题卡上的非答题区域均无效．3．非选择题的作答：用黑色签字笔直接答在答题卡对应的答题区域内．写在试卷、草稿纸和答题卡上的非答题区域均无效．4．选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑．答案写在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效．5．考试结束后，请将本试卷和答题卡一并上交．一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={}x x a >，B={}232x x x -+>0，若A ∪B=B ，则实数a 的取值范围是(A) (),1-∞ (B) (],1-∞ (C) ()2,+∞ (D) [)2,+∞ 2．欧拉公式cos sin ix e x i x =+ (i 为虚数单位)是由瑞士著名数学家欧拉发明的，他将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”．根据欧拉公式可知，3i e 表示的复数在复平面中位于(A)第一象限 (B)第二象限(C)第三象限(D)第四象限 3．给出以下三种说法： ①命题“2000,13x R x x ∃∈+>”的否定是“2,13x R x x ∀∈+<”；②已知,p q 为两个命题，若p q ∨为假命题，则()()p q ⌝∧⌝为真命题；③命题“,a b 为直线，α为平面，若//,//,a b αα，则//a b ”为真命题．其中正确说法的个数为(A)3个 (B)2个(C)1个 (D)0个 4．已知4cos 45πα⎛⎫-=⎪⎝⎭，则sin 2α= (A) 725- (B) 15- (C) 15 (D) 7255．直线40x y m ++=交椭圆2116x y +=于A ，B 两点，若线段AB 中点的横坐标为l ，则，m=(A)－2 (B)－1 (C)1 (D)26．执行如图所示的程序框图，则输出的a =(A)6.8 (B)6.5(C)6.25 (D)67．已知定义域为R 的奇函数()f x 在(0，+∞)上的解析式为()()()23log 5,0233,,2x x f x f x x ⎧-<≤⎪⎪=⎨⎪->⎪⎩则()()32018f f +=(A)－2 (B)－1 (C)1 (D)28．一种电子计时器显示时间的方式如图所示，每一个数字都在固定的全等矩形“显示池”中显示，且每个数字都由若干个全等的深色区域“▂”组成．已知在一个显示数字8的显示池中随机取一点A ，点A 落在深色区域内的概率为12，若在一个显示数字0的显示池中随机取一点B ，则点B 落在深色区域内的概率为(A) 67 (B) 37 (C) 34 (D) 389．记不等式组10,330,10x y x y x y -+≥⎧⎪--≤⎨⎪+-≥⎩，所表示的平面区域为D ，若对任意点(00,x y )∈D ，不等式0020x y c -+≤恒成立，则c 的取值范围是(A) (],4-∞- (B) (],1-∞- (C) [)4,-+∞ (D) [)1,-+∞10．如图是某几何体的三视图，则该几何体的体积为(A) 13π+ (B) 223π+(C) 23π+ (D) 123π+ 11．已知双曲线C ：()222210,0x y a b a b-=>>的左、右焦点分别为F 1，F 2，点A 为双曲线C 虚轴的一个端点，若线段AF 2与双曲线右支交于点B ，且112::AF BF BF =3：4：2，则双曲线C 的离心率为(A) 2 (B) 2(C) (D) 12．在△ABC 中，D 为边BC 上的点，且满足∠DAC=90°，sin ∠BAD=13，若S △ADC =3S △ABD ，则cosC=(A) 3 (B) 3 (C) 23 (D) 3二、填空题：本题共4小题，每小题5分，共20分。

山东省实验中学东校高三模拟理科数学 2018.11本试卷分选择题和非选择题两部分，共5页，满分150分，考试用时120分钟。

注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名和考生号、试室号、座位号等填写在答题卡上，并用2B铅笔在答题卡上的相应位置填涂考生号。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

3．回答第Ⅱ卷时，用黑色钢笔或签字笔将答案写在答卷上。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题目要求。

1.已知集合，则（）A．B．C．D．2.记复数的共轭复数为，已知复数满足，则（）A．B．C．D．3.下列函数中，既是偶函数又有零点的是（）A．B．C．D．4.设，，则是成立的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.函数的部分图象可能是（）A．B．C．D．6.在等差数列中，，则（）A．8 B．12 C．16 D．207.已知，，，则（）A．B．C．D．8.已知函数在一个周期内的图像如图所示，其中分别是这段图像的最高点和最低点，是图像与轴的交点，且，则的值为（）A．B．C．D．9.如图，在平面四边形ABCD中，，，，. 若点E为边CD上的动点，则的最小值为（）A．B．C．D．10.设是各项为正数的等比数列，是其公比，是其前项的积，且，，则下列结论错误．．的是（）A．B．C．D．与均为的最大值11.等边三角形边长为2，点是所在平面内一点，且满足，若，则的最小值是（）A．B．C．D．12.设函数是奇函数的导函数，当时，，则使得成立的的取值范围是（）A．B．C．D．第Ⅱ卷二、填空题（每小题5分，满分20分）13.已知向量，若，则__________．14.已知，，则．15.由曲线，与直线，所围成图形的面积为________．16.在中，为的中点，，点与点在直线的异侧，且，则四边形的面积的最大值为_______.三、解答题：解答应写出文字说明、证明过程或演算步骤。

2018届山东省实验中学高三上学期第三次诊断考试数学（理）试题数学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、单选题1．设集合{}{}260,2A x x x B x x =--≤=≥，则集合A B ⋂=（）A ． []2,3-B ． []2,2-C ． (]0,3D ． []2,32．设向量()(),1,4,,//a x b x a b ==且，则实数x 的值是（）A ． 0B ． 2-C ． 2D ． ±23．3．已知,x y 满足约束条件{2 212y xx y z x y x ≥+≤=+≥，则的最大值为（）A ． 32 B ． 52 C ．3 D ． 44．设,αβ是两个不同的平面，直线m α⊂．则“//m β”是“//αβ”的（） A ． 充分而不必要条件 B ． 必要而不充分条件C ． 充分必要条件D ． 既不充分也不必要条件5．已知等差数列{}n a 的前n 项和为n S ，若45624,48a a S +==，则公差d 的值为：（） A ． 1 B ． 2 C ． 4 D ． 86．已知不共线的两个向量(),22a b a b a a b b -=⊥-= 满足且，则（）A ．B ． 2C ．D ． 47．中国古代数学名著《九章算术》中有这样一个问题：今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰：“我羊食半马．”马主曰：“我马食半牛．”今欲衰偿之，问各出几何?此问题的译文是：今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟．羊主人说：“我羊所吃的禾苗只有马的一半.”马主人说：“我马所吃的禾苗只有牛的一半.”打算按此比率偿还，他们各应偿还多少?已知牛、马、羊的主人应偿还a 升，b 升，c 升，1斗为10升；则下列判断正确的是（） A ． ,,a b c 依次成公比为2的等比数列，且507a = B ． ,,a b c 依次成公比为2的等比数列，且507c = C ． ,,a b c 依次成公比为12的等比数列，且507a = D ． ,,a b c 依次成公比为12的等比数列，且507c = 8．函数()()sin ln 2x f x x =+的图象可能是（） A ． B ． C ． D ． 9．如图是函数()sin ,0,0,02y x x R A πωϕωϕ⎛⎫=+∈>><< ⎪⎝⎭在区间566ππ⎡⎤-⎢⎥⎣⎦，上的图象，为了得到这个函数的图象，只需将y =sin x 的图象（） A ． 向左平移3π个长度单位，再把所得各点的横坐标变为原来的12，纵坐标不变此卷只装订不密封班级姓名准考证号考场号座位号B ． 向左平移至3π个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变C ． 向左平移6π个长度单位，再把所得各点的横坐标变为原来的12，纵坐标不变D ． 向左平移6π个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变10．三棱锥P ABC PA -⊥中，面ABC，1,AC BC AC BC PA ⊥===，，则该三棱锥外接球的表面积为（）A ．B ． 5πC ． 20πD ． 72π11．为了竖一块广告牌，要制造三角形支架，如图，要求60ACB ∠=︒，BC 的长度大于1米，且AC 比AB 长0.5米，为了稳固广告牌，要求AC 越短越好，则AC 最短为（ ）A ．1⎛+⎝⎭米 B ． 2米 C ．(1+米 D ．(2米12．已知定义在R 的函数()f x 是偶函数，且满足()()[]2202f x f x +=-，在，上的解析式为()21,01{1,12x x f x x x -≤<=-≤≤，过点()3,0-作斜率为k 的直线l ，若直线l 与函数()f x 的图象至少有4个公共点，则实数k 的取值范围是（）A ． 11,33⎛⎫- ⎪⎝⎭B ．1,63⎛-+ ⎝ C ．1,63⎛-- ⎝ D ．163⎛⎫- ⎪⎝⎭二、填空题13．若点()4,tan θ在函数2log y x =的图象上，则sin cos θθ⋅=__________．14．一简单组合体的三视图如图，则该组合体的体积为________．15．已知函数()()sin 01f x x x a b π=<<≠，若，且()()f a f b =，则41a b +的最小值为_____________. 16．己知数列{}111212312391:,,,,,,23344410101010n n n n a b a a ++++⋅⋅⋅+++⋅⋅⋅+⋅⋅⋅=⋅若，数列{}n b 的前n 项和记为n S ，则2018S =_________. 三、解答题 17．已知函数()22cos 1,f x x x x R =+-∈． (1)求函数()f x 的最小正周期和单调递减区间； (2)在ABC ∆中，A ，B ，C 的对边分别为a,b,c,()1,sin 2sin c f C B A ===，求,a b 的值．18．已知数列{}n a 的前n 项和为()211,5,1n n n S a nS n S n n +=-+=+. (I)求证：数列n S n ⎧⎫⎨⎬⎩⎭为等差数列； (II)令2n n n b a =，求数列{}n b 的前n 项和n T ． 19．（本小题满分12分） 某省电视台为了解该省卫视一档成语类节目的收视情况，抽查东西两部各5个城市，得到观看该节目的人数(单位：千人)如下茎叶图所示，其中一个数字被污损． (I)求东部观众平均人数超过西部观众平均人数的概率．(II)节目的播出极大激发了观众随机统计了4位观众的周均学习成语知识的的时间y (单位：小时)与年龄x (单位：岁)，并制作了对照表(如下表所示)：由表中数据分析，x ，y 呈线性相关关系，试求线性回归方程y =b x +a ，并预测年龄为60岁观众周均学习成语知识的时间．参考数据：线性回归方程中b ,a 的最小二乘估计分别是b =n i =1x i y i −nxy n i =1x i 2−n x 2,a =y −bx ． 20．如图，三棱柱111ABC A B C -中，M ，N 分别为111,CC A B 的中点．(1)证明：直线MN//平面CAB 1；(2)若四边形ABB 1A 1是菱形，且160ABB ∠= ，112,,AB BC CA CB CA CB ===⊥，求平面1ABC 和平面111A B C 所成的角(锐角)的余弦值．21．已知函数()()1ln 1.1x f x x ++=+(1)求函数()y f x =的最大值；(2)令()()()()()212g x x f x a x x g x =+--+，若既有极大值，又有极小值，求实数a 的范围；(3)求证：当以*222111,2111323n N n n ⎛⎫⎛⎫⎛⎫∈≥++⋅⋅⋅+< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭时，． 22．在极坐标系中，点M 的坐标为3,2π⎛⎫ ⎪⎝⎭，曲线C的方程为4πρθ⎛⎫=+ ⎪⎝⎭；以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，斜率为1-的直线l 经过点M ．(I)求直线l 和曲线C 的直角坐标方程：(II)若P 为曲线C 上任意一点，直线l 和曲线C 相交于A ，B 两点，求△PAB 面积的最大值．23．已知函数(),f x x a a R =-∈(I)当1a =时，求()11f x x ≥++的解集；(II)若不等式()30f x x +≤的解集包含{}1x x ≤-，求a 的取值范围2018届山东省实验中学高三上学期第三次诊断考试数学（理）试题数学 答 案参考答案1．D 【解析】集合{}260A x x x =--≤{}|23x x =-≤≤，根据集合的交集的概念得到集合[]2,3A B ⋂=。

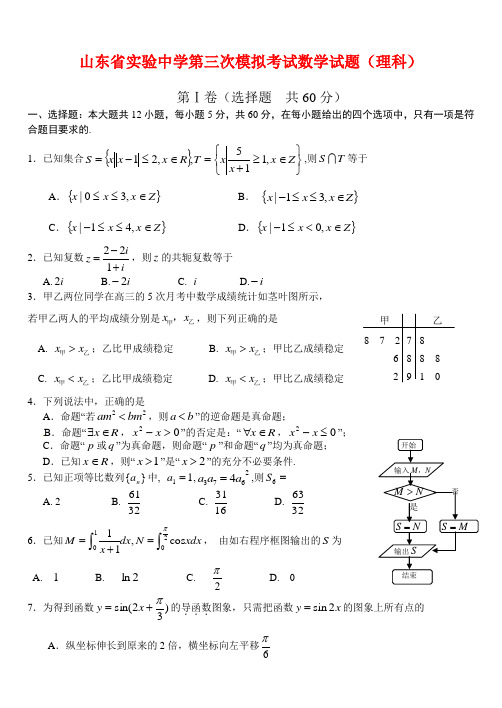
输出S 结束否开始 输入M ，NN S =M S =N M >是7 8 9 8 7 2 8 8 1 082 6 乙 甲 山东省实验中学第三次模拟考试数学试题（理科）第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}⎭⎬⎫⎩⎨⎧∈≥+=∈≤-=Z x x xT R x x x S ,115,,21,则T S 等于A ．{}Z x x x ∈≤≤,30|B ． {}|13,x x x Z -≤≤∈C ．{}Z x x x ∈≤≤-,41|D ．{}Z x x x ∈<≤-,01| 2．已知复数221iz i-=+，则z 的共轭复数等于 A.i 2 B.i 2- C. i D.i -3．甲乙两位同学在高三的5次月考中数学成绩统计如茎叶图所示，若甲乙两人的平均成绩分别是x x 乙甲，，则下列正确的是 A. x x >乙甲；乙比甲成绩稳定 B. x x >乙甲；甲比乙成绩稳定 C. x x <乙甲；乙比甲成绩稳定 D. x x <乙甲；甲比乙成绩稳定 4．下列说法中，正确的是A ．命题“若22am bm <，则a b <”的逆命题是真命题；B ．命题“x R ∃∈，02>-x x ”的否定是：“x R ∀∈，02≤-x x ”； C ．命题“p 或q ”为真命题，则命题“p ”和命题“q ”均为真命题； D ．已知R x ∈，则“1x >”是“2x >”的充分不必要条件. 5．已知正项等比数列}{n a 中, 11=a ,26734a a a =,则=6SA. 2B. 3261C. 1631D.32636．已知12001,cos 1M dx N xdx x π==+⎰⎰， 由如右程序框图输出的S 为A. 1B. 2lnC. 2πD. 0 7．为得到函数)32sin(π+=x y 的导函数．．．图象，只需把函数sin 2y x =的图象上所有点的 A ．纵坐标伸长到原来的2倍，横坐标向左平移6πB ．纵坐标缩短到原来的12倍，横坐标向左平移3π C ．纵坐标伸长到原来的2倍，横坐标向左平移125πD ．纵坐标缩短到原来的12倍，横坐标向左平移65π8. 为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入相关数据组成传输信息，设定原信息为}{),2,1,0(1,0,210=∈i a a a a i 传输信息为,12100h a a a h 其中201100,a h h a a h ⊕=⊕=，⊕运算规则为.011,101,110,000=⊕=⊕=⊕=⊕例如原信息为111，则传输信息为01111，传输信息在传输过程中受到干扰可能导致接受信息出错，则下列接受信息一定有误的是 A ． 11010 B ．01100 C ．10111 D ．000119. 若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为A ．163πB ．193πC ．43πD ．1912π10. 直线x my 2=与圆0422=-+++ny mx y x 交于M 、N 两点，且M 、N 关于直线0=+y x 对称，则弦MN 的长为A. 2B. 3C. 4D. 511.已知方程：220x ax b ++= (,)a R b R ∈∈，其一根在区间(0,1)内,另一根在区间(1,2)内，则22(3)z a b =++的取值范围为A. 2(,2) B. 1(,4)2C. (1,2)D. (1,4) 12. 设()f x 是R 上的可导函数，且满足()()f x f x >'，对任意的正实数a ，下列不等式恒成立的是A.()(0)af a e f <； B.()(0)af a e f >； C.(0)()a f f a e <； D.(0)()af f a e >； 第Ⅱ卷（非选择题 共90分）二、填空题：本大题共有4个小题，每小题4分，共计16分,请将答案写在答题纸的相应位置. 13. 二项式 6()x x-的展开式中的常数项是__________. 14. 过双曲线12222=-by a x 的左焦点F 作⊙O : 222a y x =+的两条切线，记切点为A,B,双曲线左顶点为C ，若120=∠ACB ,则双曲线的离心率为____________.15. 将4名新来的同学分配到A 、B 、C 三个班级中，每个班级至少安排1名学生，其中甲同学不能分1D1C 1B1ACDAB第19题配到A 班，那么不同的分配方案方法种数为______________（用数字作答）.16. 在△ABC 中，过中线AD 的中点E 任作一直线分别交边AB ，AC 于M 、N 两点，设,,(0)AM xAB AN y AC xy ==≠则4x y +的最小值是_________三、解答题：本大题共6个小题.共74分.解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）设△ABC 三个角A ，B ，C 的对边分别为a ，b ，c ，向量)2,(b a p =，)1,(sin A q =，且q p //． （Ⅰ）求角B 的大小；（Ⅱ）若△ABC 是锐角三角形，)tan cos sin ,1(),cos ,(cos B A A B A -==，求n m ⋅的取值范围． 18．（本小题满分12分）山东省某示范性高中为了推进新课程改革，满足不同层次学生的需求，决定从高一年级开始，在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座，每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座，也可以放弃任何一门科目的辅导讲座。

2018年高考理科数学模拟试卷（一）（考试时间120分钟满分150分）一、选择题（共12小题，每小题5分，满分60分）1．已知集合S={1，2}，设S的真子集有m个，则m=（）A．4 B．3 C．2 D．12．已知i为虚数单位，则的共轭复数为（）A．﹣+i B． +i C．﹣﹣i D．﹣i3．已知、是平面向量，如果||=3，||=4，|+|=2，那么|﹣|=（）A． B．7 C．5 D．4．在（x﹣）10的二项展开式中，x4的系数等于（）A．﹣120 B．﹣60 C．60 D．1205．已知a，b，c，d都是常数，a＞b，c＞d，若f（x）=2017﹣（x﹣a）（x﹣b）的零点为c，d，则下列不等式正确的是（）A．a＞c＞b＞d B．a＞b＞c＞d C．c＞d＞a＞b D．c＞a＞b＞d6．公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π，他从圆内接正六边形算起，令边数一倍一倍地增加，即12，24，48，…，192，…，逐个算出正六边形，正十二边形，正二十四边形，…，正一百九十二边形，…的面积，这些数值逐步地逼近圆面积，刘徽算到了正一百九十二边形，这时候π的近似值是3.141024，刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的，用有限来逼近无穷，这种思想及其重要，对后世产生了巨大影响，如图是利用刘徽的“割圆术”思想设计的一个程序框图，若运行改程序（参考数据：≈1.732，sin15°≈0.2588，sin7.5°≈0.1305），则输出n的值为（）A．48 B．36 C．30 D．247．在平面区域内随机取一点（a，b），则函数f（x）=ax2﹣4bx+1在区间[1，+∞）上是增函数的概率为（）A． B．C．D．8．已知△ABC的内角A、B、C的对边分别为a、b、c．若a=bcosC+csinB，且△ABC的面积为1+．则b的最小值为（）A．2 B．3 C．D．9．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）A．12 B．18 C．24 D．3010．已知常数ω＞0，f（x）=﹣1+2sinωxcosωx+2cos2ωx图象的对称中心得到对称轴的距离的最小值为，若f（x0）=，≤x0≤，则cos2x0=（）A．B．C．D．11．已知三棱锥P﹣ABC的所有顶点都在表面积为16π的球O的球面上，AC为球O的直径，当三棱锥P﹣ABC的体积最大时，设二面角P﹣AB﹣C的大小为θ，则sinθ=（）A． B．C．D．12．抛物线M的顶点是坐标原点O，抛物线M的焦点F在x轴正半轴上，抛物线M的准线与曲线x2+y2﹣6x+4y﹣3=0只有一个公共点，设A是抛物线M上的一点，若•=﹣4，则点A的坐标是（）A．（﹣1，2）或（﹣1，﹣2）B．（1，2）或（1，﹣2）C．（1，2） D．（1，﹣2）二、填空题（共4小题，每小题5分，满分20分）13．某校1000名高三学生参加了一次数学考试，这次考试考生的分数服从正态分布N（90，σ2），若分数在（70，110]内的概率为0.7，估计这次考试分数不超过70分的人数为人．14．过双曲线﹣=1（a＞0，b＞0）的右焦点且垂直于x轴的直线与双曲线交于A，B两点，与双曲线的渐近线交于C，D两点，若|AB|≥|CD|，则双曲线离心率的取值范围为．15．计算=（用数字作答）16．已知f（x）=，若f （x﹣1）＜f（2x+1），则x的取值范围为．三、解答题（共5小题，满分60分）17．设数列{a n}的前n项和为S n，a1=1，当n≥2时，a n=2a n S n﹣2S n2．（1）求数列{a n}的通项公式；（2）是否存在正数k，使（1+S1）（1+S2）…（1+S n）≥k对一切正整数n都成立？若存在，求k的取值范围，若不存在，请说明理由．18．云南省20XX年高中数学学业水平考试的原始成绩采用百分制，发布成绩使用等级制，各登记划分标准为：85分及以上，记为A等，分数在[70，85）内，记为B等，分数在[60，70）内，记为C等，60分以下，记为D等，同时认定等级分别为A，B，C都为合格，等级为D为不合格．已知甲、乙两所学校学生的原始成绩均分布在[50，100]内，为了比较两校学生的成绩，分别抽取50名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]分别作出甲校如图1所示样本频率分布直方图，乙校如图2所示样本中等级为C、D的所有数据茎叶图．（1）求图中x的值，并根据样本数据比较甲乙两校的合格率；（2）在选取的样本中，从甲、乙两校C等级的学生中随机抽取3名学生进行调研，用X表示所抽取的3名学生中甲校的学生人数，求随机变量X的分布列和数学期望．19．如图，在四棱锥S﹣ABCD中，底面ABCD是矩形，平面ABCD⊥平面SBC，SB=SC，M是BC的中点，AB=1，BC=2．（1）求证：AM⊥SD；（2）若二面角B﹣SA﹣M的正弦值为，求四棱锥S﹣ABCD的体积．20．已知椭圆E的中心在原点，焦点F1、F2在y轴上，离心率等于，P 是椭圆E上的点，以线段PF1为直径的圆经过F2，且9•=1．（1）求椭圆E的方程；（2）做直线l与椭圆E交于两个不同的点M、N，如果线段MN被直线2x+1=0平分，求l的倾斜角的取值范围．21．已知e是自然对数的底数，实数a是常数，函数f（x）=e x﹣ax﹣1的定义域为（0，+∞）．（1）设a=e，求函数f（x）在切点（1，f（1））处的切线方程；（2）判断函数f（x）的单调性；（3）设g（x）=ln（e x+x3﹣1）﹣lnx，若∀x＞0，f（g（x））＜f（x），求a 的取值范围．[选修4-4：坐标系与参数方程选讲]22．已知直线L的参数方程为（t为参数），以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=．（Ⅰ）直接写出直线L的极坐标方程和曲线C的普通方程；（Ⅱ）过曲线C上任意一点P作与L夹角为的直线l，设直线l与直线L的交点为A，求|PA|的最大值．[选修4-5：不等式选讲]23．已知函数f（x）=|x+a|+|x﹣2|的定义域为实数集R．（Ⅰ）当a=5时，解关于x的不等式f（x）＞9；（Ⅱ）设关于x的不等式f（x）≤|x﹣4|的解集为A，B={x∈R|2x﹣1|≤3}，如果A∪B=A，求实数a的取值范围．参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．解：∵集合S={1，2}，∴S的真子集的个数为：22﹣1=3．故选：B．2．解：∵=，∴的共轭复数为．故选：C．3．解：根据条件：==4；∴；∴=9﹣（﹣21）+16=46；∴．故选：A．==（﹣1）r x10﹣2r，4．解：通项公式T r+1令10﹣2r=4，解得r=3．∴x4的系数等于﹣=﹣120．故选：A5．解：由题意设g（x）=（x﹣a）（x﹣b），则f（x）=2017﹣g（x），所以g（x）=0的两个根是a、b，由题意知：f（x）=0 的两根c，d，也就是g（x）=2017 的两根，画出g（x）（开口向上）以及直线y=2017的大致图象，则与f（x）交点横坐标就是c，d，f（x）与x轴交点就是a，b，又a＞b，c＞d，则c，d在a，b外，由图得，c＞a＞b＞d，故选D．6．解：模拟执行程序，可得：n=6，S=3sin60°=，不满足条件S≥3.10，n=12，S=6×sin30°=3，不满足条件S≥3.10，n=24，S=12×sin15°=12×0.2588=3.1056，满足条件S≥3.10，退出循环，输出n的值为24．故选：D．7．解：作出不等式组对应的平面区域如图：对应的图形为△OAB，其中对应面积为S=×4×4=8，若f（x）=ax2﹣4bx+1在区间[1，+∞）上是增函数，则满足a＞0且对称轴x=﹣≤1，即，对应的平面区域为△OBC，由，解得，∴对应的面积为S1=××4=，∴根据几何概型的概率公式可知所求的概率为=，故选：B．8．解：由正弦定理得到：sinA=sinCsinB+sinBcosC，∵在△ABC中，sinA=sin[π﹣（B+C）]=sin（B+C），∴sin（B+C）=sinBcosC+cosBsinC=sinCsinB+sinBcosC，∴cosBsinC=sinCsinB，∵C∈（0，π），sinC≠0，∴cosB=sinB，即tanB=1，∵B∈（0，π），∴B=，=acsinB=ac=1+，∵S△ABC∴ac=4+2，由余弦定理得到：b2=a2+c2﹣2accosB，即b2=a2+c2﹣ac≥2ac﹣ac=4，当且仅当a=c时取“=”，∴b的最小值为2．故选：A．9．解：由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥，切去一个三棱锥所得的组合体，其底面面积S=×3×4=6，棱柱的高为：5，棱锥的高为3，故组合体的体积V=6×5﹣×6×3=24，故选：C10．解：由f（x）=﹣1+2sinωxcosωx+2cos2ωx，化简可得：f（x）=sin2ωx+cos2ωx=2sin（2ωx+）∵对称中心得到对称轴的距离的最小值为，∴T=π．由，可得：ω=1．f（x0）=，即2sin（2x0+）=∵≤x0≤，∴≤2x0+≤∴sin（2x0+）=＞0∴cos（2x0+）=．那么：cos2x0=cos（2x0+﹣）=cos（2x0+）cos+sin（2x0+）sin=故选D11．解：如图所示：由已知得球的半径为2，AC为球O的直径，当三棱锥P﹣ABC的体积最大时，△ABC为等腰直角三角形，P在面ABC上的射影为圆心O，过圆心O作OD⊥AB于D，连结PD，则∠PDO为二面角P﹣AB﹣C的平面角，在△ABC△中，PO=2，OD=BC=，∴，sinθ=．故选：C12．解：x2+y2﹣6x+4y﹣3=0，可化为（x﹣3）2+（y+2）2=16，圆心坐标为（3，﹣2），半径为4，∵抛物线M的准线与曲线x2+y2﹣6x+4y﹣3=0只有一个公共点，∴3+=4，∴p=2．∴F（1，0），设A（，y0）则=（，y0），=（1﹣，﹣y0），由•=﹣4，∴y0=±2，∴A（1，±2）故选B．二、填空题（共4小题，每小题5分，满分20分）13．解：由X服从正态分布N（90，σ2）（σ＞0），且P（70≤X≤110）=0.35，得P（X≤70）=（1﹣0.35）=．∴估计这次考试分数不超过70分的人数为1000×=325．故答案为：325．14．解：设双曲线﹣=1（a＞0，b＞0）的右焦点为（c，0），当x=c时代入双曲线﹣=1得y=±，则A（c，），B（c，﹣），则AB=，将x=c代入y=±x得y=±，则C（c，），D（c，﹣），则|CD|=，∵|AB|≥|CD|，∴≥•，即b≥c，则b2=c2﹣a2≥c2，即c2≥a2，则e2=≥，则e≥．故答案为：[，+∞）．15．解：由===．故答案为：．16．解：∵已知f（x）=，∴满足f（﹣x）=f（x），且f（0）=0，故f（x）为偶函数，f（x）在[0，+∞）上单调递增．若f（x﹣1）＜f（2x+1），则|x﹣1|＜|2x+1|，∴（x﹣1）2＜（2x+1）2，即x2+2x＞0，∴x＞0，或x＜﹣2，故答案为：{x|x＞0，或x＜﹣2}．三、解答题（共5小题，满分60分）17．解：（1）∵当n≥2时，a n=2a n S n﹣2S n2，∴a n=，n≥2，∴（S n﹣S n﹣1）（2S n﹣1）=2S n2，∴S n﹣S n﹣1=2S n S n﹣1，∴﹣2，n≥2，∴数列{}是以=1为首项，以2为公差的等差数列，∴=1+2（n﹣1）=2n﹣1，∴S n=，∴n≥2时，a n=S n﹣S n﹣1=﹣=﹣，∵a1=S1=1，∴a n=，（2）设f（n）=，则==＞1，∴f（n）在n∈N*上递增，要使f（n）≥k恒成立，只需要f（n）min≥k，∵f（n）min=f（1）=，∴0＜k≤18．解：（1）由频率分布直方图可得：（x+0.012+0.056+0.018+0.010）×10=1，解得x=0.004．甲校的合格率P1=（1﹣0.004）×10=0.96=96%，乙校的合格率P2==96%．可得：甲乙两校的合格率相同，都为96%．（2）甲乙两校的C等级的学生数分别为：0.012×10×50=6，4人．X=0，1，2，3．则P（X=k）=，P（X=0）==，P（X=1）==，P（X=2）==，P（X=3）==．∴X的分布列为：X0123PE（X）=0+1×+2×+3×=．19．证明：（1）∵SB=SC，M是BC的中点，∴SM⊥BC，∵平面ABCD⊥平面SBC，平面ABCD∩平面SBC=BC，∴SM⊥平面ABCD，∵AM⊂平面ABCD，∴SM⊥AM，∵底面ABCD是矩形，M是BC的中点，AB=1，BC=2，∴AM2=BM2==，AD=2，∴AM2+BM2=AD2，∴AM⊥DM，∵SM∩DM=M，∴AM⊥平面DMS，∵SD⊂平面DMS，∴AM⊥SD．解：（2）∵SM⊥平面ABCD，∴以M为原点，MC为x轴，MS为y轴，过M作平面BCS的垂线为z轴，建立空间直角坐标系，设SM=t，则M（0，0，0），B（﹣1，0，0），S（0，t，0），A（﹣1，0，1），=（0，0，1），=（1，t，0），=（﹣1，0，1），=（0，t，0），设平面ABS的法向量=（x，y，z），则，取x=1，得=（1，﹣，0），设平面MAS的法向量=（a，b，c），则，取a=1，得=（1，0，1），设二面角B﹣SA﹣M的平面角为θ，∵二面角B﹣SA﹣M的正弦值为，∴sinθ=，cosθ==，∴cosθ===，解得t=，∵SM⊥平面ABCD，SM=，∴四棱锥S﹣ABCD的体积：V S﹣=== ABCD．20．解：（1）由题意可知：设题意的方程：（a＞b＞0），e==，则c=a，设丨PF1丨=m，丨PF2丨=n，则m+n=2a，线段PF1为直径的圆经过F2，则PF2⊥F1F2，则n2+（2c）2=m2，9m•n×cos∠F1PF2=1，由9n2=1，n=，解得：a=3，c=，则b==1，∴椭圆标准方程：；（2）假设存在直线l，依题意l交椭圆所得弦MN被x=﹣平分，∴直线l的斜率存在．设直线l：y=kx+m，则由消去y，整理得（k2+9）x2+2kmx+m2﹣9=0∵l与椭圆交于不同的两点M，N，∴△=4k2m2﹣4（k2+9）（m2﹣9）＞0，即m2﹣k2﹣9＜0①设M（x1，y1），N（x2，y2），则x1+x2=﹣∴=﹣=﹣，∴m=②把②代入①式中得（）2﹣（k2+9）＜0∴k＞或k＜﹣，∴直线l倾斜角α∈（，）∪（，）．21．解：（1）a=e时，f（x）=e x﹣ex﹣1，f（1）=﹣1，f′（x）=e x﹣e，可得f′（1）=0，故a=e时，函数f（x）在切点（1，f（1））处的切线方程是y=﹣1；（2）f（x）=e x﹣ax﹣1，f′（x）=e x﹣a，当a≤0时，f′（x）＞0，则f（x）在R上单调递增；当a＞0时，令f′（x）=e x﹣a=0，得x=lna，则f（x）在（﹣∞，lna]上单调递减，在（lna，+∞）上单调递增．（3）设F（x）=e x﹣x﹣1，则F′（x）=e x﹣1，∵x=0时，F′（x）=0，x＞0时，F′（x）＞0，∴F（x）在[0，+∞）递增，∴x＞0时，F（x）＞F（0），化简得：e x﹣1＞x，∴x＞0时，e x+x3﹣1＞x，设h（x）=xe x﹣e x﹣x3+1，则h′（x）=x（e x﹣ex），设H（x）=e x﹣ex，H′（x）=e x﹣e，由H′（x）=0，得x=1时，H′（x）＞0，x＜1时，H′（x）＜0，∴x＞0时，H（x）的最小值是H（1），x＞0时，H（x）≥H（1），即H（x）≥0，∴h′（x）≥0，可知函数h（x）在（0，+∞）递增，∴h（x）＞h（0）=0，化简得e x+x3﹣1＜xe x，∴x＞0时，x＜e x+x3﹣1＜xe x，∴x＞0时，lnx＜ln（e x+x3﹣1）＜lnx+x，即0＜ln（e x+x3﹣1）﹣lnx＜x，即x＞0时，0＜g（x）＜x，当a≤1时，由（2）得f（x）在（0，+∞）递增，得f（g（x））＜f（x）满足条件，当a＞1时，由（2）得f（x）在（0，lna）递减，∴0＜x≤lna时，f（g（x））＞f（x），与已知∀x＞0，f（g（x））＜f（x）矛盾，综上，a的范围是（﹣∞，1]．[选修4-4：坐标系与参数方程选讲]22．解：（Ⅰ）直线L的参数方程为（t为参数），普通方程为2x+y﹣6=0，极坐标方程为2ρcosθ+ρsinθ﹣6=0，曲线C的极坐标方程为ρ=，即ρ2+3ρ2cos2θ=4，曲线C 的普通方程为=1；（Ⅱ）曲线C上任意一点P（cosθ，2sinθ）到l的距离为d=|2cosθ+2sinθ﹣6|．则|PA|==|2sin（θ+45°）﹣6|，当sin（θ+45°）=﹣1时，|PA|取得最大值，最大值为．[选修4-5：不等式选讲]23．解：（Ⅰ）当a=5时，关于x的不等式f（x）＞9，即|x+5|+|x﹣2|＞9，故有①；或②；或③．解①求得x＜﹣6；解②求得x∈∅，解③求得x＞3．综上可得，原不等式的解集为{x|x＜﹣6，或x＞3}．（Ⅱ）设关于x的不等式f（x）=|x+a|+|x﹣2|≤|x﹣4|的解集为A，B={x∈R|2x﹣1|≤3}={x|﹣1≤x≤2 }，如果A∪B=A，则B⊆A，∴，即，求得﹣1≤a≤0，故实数a的范围为[﹣1，0]．2018年高考理科数学模拟试卷（二）（考试时间120分钟满分150分）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1．复数z满足方程=﹣i（i为虚数单位），则复数z在复平面内对应的点在（）A．第一象限B．第二象限C．第三象限D．第四象限2．已知集合A={x|x2+x﹣2＜0}，集合B={x|（x+2）（3﹣x）＞0}，则（∁R A）∩B 等于（）A．{x|1≤x＜3}B．{x|2≤x＜3}C．{x|﹣2＜x＜1}D．{x|﹣2＜x≤﹣1或2≤x＜3}3．下列函数中，在其定义域内，既是奇函数又是减函数的是（）A．f（x）=B．f（x）=C．f（x）=2﹣x﹣2x D．f（x）=﹣tanx 4．已知“x＞2”是“x2＞a（a∈R）”的充分不必要条件，则a的取值范围是（）A．（﹣∞，4）B．（4，+∞）C．（0，4]D．（﹣∞，4]5．已知角α是第二象限角，直线2x+（t anα）y+1=0的斜率为，则cosα等于（）A． B．﹣C．D．﹣6．执行如图所示的程序框图，若输入n的值为8，则输出s的值为（）A．16 B．8 C．4 D．27．（﹣）8的展开式中，x的系数为（）A．﹣112 B．112 C．56 D．﹣568．在△ABC中，∠A=60°，AC=3，面积为，那么BC的长度为（）A．B．3 C．2D．9．记曲线y=与x轴所围成的区域为D，若曲线y=ax（x ﹣2）（a＜0）把D的面积均分为两等份，则a的值为（）A．﹣B．﹣C．﹣D．﹣10．为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分的中位数为m e，众数为m0，平均值为，则（）A．m e=m0=B．m e=m0＜C．m e＜m0＜D．m0＜m e＜11．已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB=6，BC=2，则棱锥O﹣ABCD的侧面积为（）A．20+8B．44 C．20 D．4612．函数f（x）=2sin（2x++φ）（|φ|＜）的图象向左平移个单位后关于y轴对称，则以下判断不正确的是（）A．是奇函数 B．为f（x）的一个对称中心C．f（x）在上单调递增D．f（x）在（0，）上单调递减二、填空题：本大题共4小题，每小题5分，共20分.13．若变量x，y满足约束条件，则z=2x﹣y的最大值为．14．如图所示是一个几何体的三视图，则这个几何体的体积为．15．已知抛物线y2=8x的焦点F到双曲线C：﹣=1（a＞0，b＞0）渐近线的距离为，点P是抛物线y2=8x上的一动点，P到双曲线C的上焦点F1（0，c）的距离与到直线x=﹣2的距离之和的最小值为3，则该双曲线的方程为．16．已知向量，的夹角为θ，|+|=2，|﹣|=2则θ的取值范围为．三、解答题：本大题共5小题，共70分.解答应写出必要的文字说明或推理、验算过程.17．已知S n为等差数列{a n}的前n项和，S6=51，a5=13．（1）求数列{a n}的通项公式；（2）数列{b n}的通项公式是b n=，求数列{b n}的前n项和S n．18．袋中有大小相同的四个球，编号分别为1、2、3、4，从袋中每次任取一个球，记下其编号．若所取球的编号为偶数，则把该球编号改为3后放同袋中继续取球；若所取球的编号为奇数，则停止取球．（1）求“第二次取球后才停止取球”的概率；（2）若第一次取到偶数，记第二次和第一次取球的编号之和为X，求X的分布列和数学期望．19．在三棱椎A﹣BCD中，AB=BC=4，AD=BD=CD=2，在底面BCD内作CE ⊥CD，且CE=．（1）求证：CE∥平面ABD；（2）如果二面角A﹣BD﹣C的大小为90°，求二面角B﹣AC﹣E的余弦值．20．在平面直角坐标系xOy中，已知椭圆C： +=1（a＞b＞0）的离心率为．且过点（3，﹣1）．（1）求椭圆C的方徎；（2）若动点P在直线l：x=﹣2上，过P作直线交椭圆C于M，N两点，使得PM=PN，再过P作直线l′⊥MN，直线l′是否恒过定点，若是，请求出该定点的坐标；若否，请说明理由．21．已知函数f（x）=m（x﹣1）2﹣2x+3+lnx（m≥1）．（1）求证：函数f（x）在定义域内存在单调递减区间[a，b]；（2）是否存在实数m，使得曲线C：y=f（x）在点P（1，1）处的切线l与曲线C有且只有一个公共点？若存在，求出实数m的值；若不存在，请说明理由．[选修4-1：几何证明选讲]22．选修4﹣1：几何证明选讲如图，已知PA是⊙O的切线，A是切点，直线PO交⊙O于B、C两点，D是OC 的中点，连接AD并延长交⊙O于点E，若PA=2，∠APB=30°．（Ⅰ）求∠AEC的大小；（Ⅱ）求AE的长．[选修4-4：极坐标与参数方程]23．选修4﹣4：坐标系与参数方程在平面直角坐标系x0y中，动点A的坐标为（2﹣3sinα，3cosα﹣2），其中α∈R．在极坐标系（以原点O为极点，以x轴非负半轴为极轴）中，直线C的方程为ρcos （θ﹣）=a．（Ⅰ）判断动点A的轨迹的形状；（Ⅱ）若直线C与动点A的轨迹有且仅有一个公共点，求实数a的值．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣1|+|x﹣a|．（1）若a=2，解不等式f（x）≥2；（2）若a＞1，∀x∈R，f（x）+|x﹣1|≥1，求实数a的取值范围．参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1．解：由=﹣i，得，即z=1+i．则复数z在复平面内对应的点的坐标为（1，1）．位于第一象限．故选：A．2．解：∵集合A={x|x2+x﹣2＜0}={x|﹣2＜x＜1}，集合B={x|（x+2）（3﹣x）＞0}={x|﹣2＜x＜3}，∴（C R A）∩B={x|x≤﹣2或x≥1}∩{x|﹣2＜x＜3}={x|1≤x＜3}．故选：A．3．解：A中，f（x）=是奇函数，但在定义域内不单调；B中，f（x）=是减函数，但不具备奇偶性；C中，f（x）2﹣x﹣2x既是奇函数又是减函数；D中，f（x）=﹣tanx是奇函数，但在定义域内不单调；故选C．4．解：由题意知：由x＞2能得到x2＞a；而由x2＞a得不出x＞2；∵x＞2，∴x2＞4；∴a≤4；∴a的取值范围是（﹣∞，4]．故选：D．5．解：由题意得：k=﹣=，故tanα=﹣，故cosα=﹣，故选：D．6．解：开始条件i=2，k=1，s=1，i＜8，开始循环，s=1×（1×2）=2，i=2+2=4，k=1+1=2，i＜8，继续循环，s=×（2×4）=4，i=6，k=3，i＜8，继续循环；s=×（4×6）=8，i=8，k=4，8≥8，循环停止，输出s=8；故选B：=（﹣2）r C8r x4﹣r，7．解：（﹣）8的展开式的通项为T r+1令4﹣r=1，解得r=2，∴展开式中x的系数为（﹣2）2C82=112，故选：B．8．解：在图形中，过B作BD⊥ACS△ABC=丨AB丨•丨AC丨sinA，即×丨AB丨×3×sin60°=，解得：丨AB丨=2，∴cosA=，丨AD丨=丨AB丨cosA=2×=1，sinA=，则丨BD丨=丨AB丨sinA=2×=，丨CD丨=丨AC丨﹣丨AD丨=3﹣1=2，在△BDC中利用勾股定理得：丨BC丨2=丨BD丨2+丨CD丨2=7，则丨BC丨=，故选A．9．解：由y=得（x﹣1）2+y2=1，（y≥0），则区域D表示（1，0）为圆心，1为半径的上半圆，而曲线y=ax（x﹣2）（a＜0）把D的面积均分为两等份，∴=，∴（﹣ax2）=，∴a=﹣，故选：B．10．解：根据题意，由题目所给的统计图可知：30个得分中，按大小排序，中间的两个得分为5、6，故中位数m e=5.5，得分为5的最多，故众数m0=5，其平均数=≈5.97；则有m0＜m e＜，故选：D．11．解：由题意可知四棱锥O﹣ABCD的侧棱长为：5．所以侧面中底面边长为6和2，它们的斜高为：4和2，所以棱锥O﹣ABCD的侧面积为：S=4×6+2=44．故选B．12．解：把函数f（x）=2sin（2x++φ）（|φ|＜）的图象向左平移个单位后，得到y=2sin（2x++φ+π）=﹣2sin（2x++φ）的图象，再根据所得关于y轴对称，可得+φ=kπ+，k∈Z，∴φ=，∴f（x）=2sin（2x++φ）=2cos2x．由于f（x+）=2cos（2x+）=﹣sin2x是奇函数，故A正确；当x=时，f（x）=0，故（，0）是f（x）的图象的一个对称中心，故B正确；在上，2x∈（﹣，﹣），f（x）没有单调性，故C不正确；在（0，）上，2x∈（0，π），f（x）单调递减，故D正确，故选：C．二、填空题：本大题共4小题，每小题5分，共20分.13．解：由约束条件作出可行域如图，联立，解得A（4，2），化目标函数z=2x﹣y为y=2x﹣z，由图可知，当直线y=2x﹣z过点A时，直线在y 轴上的截距最小，z有最大值为6．故答案为：6．14．解：由三视图得到几何体如图：其体积为；故答案为：15．解：抛物线y2=8x的焦点F（2，0），双曲线C：﹣=1（a＞0，b ＞0）一条渐近线的方程为ax﹣by=0，∵抛物线y2=8x的焦点F到双曲线C：﹣=1（a＞0，b＞0）渐近线的距离为，∴，∴2b=a，∵P到双曲线C的上焦点F1（0，c）的距离与到直线x=﹣2的距离之和的最小值为3，∴FF1=3，∴c2+4=9，∴c=，∵c2=a2+b2，a=2b，∴a=2，b=1，∴双曲线的方程为﹣x2=1．故答案为：﹣x2=1．16．解：由|+|=2，|﹣|=2，可得：+2=12，﹣2=4，∴=8≥2，=2，∴cosθ=≥．∴θ∈．故答案为：．三、解答题：本大题共5小题，共70分.解答应写出必要的文字说明或推理、验算过程.17．解：（1）设等差数列{a n}的公差为d，则∵S6=51，∴×（a1+a6）=51，∴a1+a6=17，∴a2+a5=17，∵a5=13，∴a2=4，∴d=3，∴a n=a2+3（n﹣2）=3n﹣2；（2）b n==﹣2•8n﹣1，∴数列{b n}的前n项和S n==（8n﹣1）．18．解：（1）记“第二次取球后才停止取球”为事件A．∴第一次取到偶数球的概率为=，第二次取球时袋中有三个奇数，∴第二次取到奇数球的概率为，而这两次取球相互独立，∴P（A）=×=．（2）若第一次取到2时，第二次取球时袋中有编号为1，3，3，4的四个球；若第一次取到4时，第二次取球时袋中有编号为1，2，3，3的四个球．∴X的可能取值为3，5，6，7，∴P（X=3）=×=，P（X=5）=×+×=，P（X=6）=×+×=，P（X=7）=×=，∴X的分布列为：X3567P数学期望EX=3×+5×+6×+7×=．19．（1）证明：∵BD=CD=2，BC=4，∴BD2+CD2=BC2，∴BD⊥CD，∵CE⊥CD，∴CE∥BD，又CE⊄平面ABD，BD⊂平面ABD，∴CE∥平面ABD；（2）解：如果二面角A﹣BD﹣C的大小为90°，由AD⊥BD得AD⊥平面BDC，∴AD⊥CE，又CE⊥CD，∴CE⊥平面ACD，从而CE⊥AC，由题意AD=DC=2，∴Rt△ADC中，AC=4，设AC的中点为F，∵AB=BC=4，∴BF⊥AC，且BF=2，设AE中点为G，则FG∥CE，由CE⊥AC得FG⊥AC，∴∠BFG为二面角B﹣AC﹣E的平面角，连接BG，在△BCE中，∵BC=4，CE=，∠BCE=135°，∴BE=，在Rt△DCE中，DE==，于是在Rt△ADE中，AE==3，在△ABE中，BG2=AB2+BE2﹣AE2=，∴在△BFG中，cos∠BFG==﹣，∴二面角B﹣AC﹣E的余弦值为﹣．20．解：（1）∵椭圆C： +=1（a＞b＞0）的离心率为．且过点（3，﹣1），∴，解得a2=12，b2=4，∴椭圆C的方程为．（2）∵直线l的方程为x=﹣2，设P（﹣2，y0），，当y0≠0时，设M（x1，y1），N（x2，y2），由题意知x1≠x2，联立，∴，∴，又∵PM=PN，∴P为线段MN的中点，∴直线MN的斜率为，又l′⊥MN，∴l′的方程为，即，∴l′恒过定点．当y0=0时，直线MN为，此时l′为x轴，也过点，综上，l′恒过定点．21．（1）证明：令f′（x）=0，得mx2﹣（m+2）x+1=0．（*）因为△=（m+2）2﹣4m=m2+4＞0，所以方程（*）存在两个不等实根，记为a，b （a＜b）．因为m≥1，所以a+b=＞0，ab=＞0，所以a＞0，b＞0，即方程（*）有两个不等的正根，因此f′（x）≤0的解为[a，b]．故函数f（x）存在单调递减区间；（2）解：因为f′（1）=﹣1，所以曲线C：y=f（x）在点P（1，1）处的切线l为y=﹣x+2．若切线l与曲线C只有一个公共点，则方程m（x﹣1）2﹣2x+3+lnx=﹣x+2有且只有一个实根．显然x=1是该方程的一个根．令g（x）=m（x﹣1）2﹣x+1+lnx，则g′（x）=．当m=1时，有g′（x）≥0恒成立，所以g（x）在（0，+∞）上单调递增，所以x=1是方程的唯一解，m=1符合题意．当m＞1时，令g′（x）=0，得x1=1，x2=，则x2∈（0，1），易得g（x）在x1处取到极小值，在x2处取到极大值．所以g（x2）＞g（x1）=0，又当x→0时，g（x）→﹣∞，所以函数g（x）在（0，）内也有一个解，即当m＞1时，不合题意．综上，存在实数m，当m=1时，曲线C：y=f（x）在点P（1，1）处的切线l与C 有且只有一个公共点．[选修4-1：几何证明选讲]22．解：（Ⅰ）连接AB，因为：∠APO=30°，且PA是⊙O的切线，所以：∠AOB=60°；∵OA=OB∴∠AB0=60°；∵∠ABC=∠AEC∴∠AEC=60°．（Ⅱ）由条件知AO=2，过A作AH⊥BC于H，则AH=，在RT△AHD中，HD=2，∴AD==．∵BD•DC=AD•DE，∴DE=．∴AE=DE+AD=．[选修4-4：极坐标与参数方程]23．解：（Ⅰ）设动点A的直角坐标为（x，y），则，利用同角三角函数的基本关系消去参数α可得，（x﹣2）2+（y+2）2=9，点A的轨迹为半径等于3的圆．（Ⅱ）把直线C方程为ρcos（θ﹣）=a化为直角坐标方程为+=2a，由题意可得直线C与圆相切，故有=3，解得a=3 或a=﹣3．[选修4-5：不等式选讲]24．解：（1）当a=2时，，由于f（x）≥2，则①当x＜1时，﹣2x+3≥2，∴x≤；②当1≤x≤1时，1≥2，无解；③当x＞2时，2x﹣3≥2，∴x≥．综上所述，不等式f（x）≥2的解集为：（﹣∞，]∪[，+∞）；（2）令F（x）=f（x）+|x﹣1|，则，所以当x=1时，F（x）有最小值F（1）=a﹣1，只需a﹣1≥1，解得a≥2，所以实数a的取值范围为[2，+∞）．2018年高考理科数学模拟试卷（三）（考试时间120分钟满分150分）一、选择题（共12小题，每小题5分，满分60分）1．已知复数z满足z（1﹣i）2=1+i（i为虚数单位），则z=（）A． +i B．﹣i C．﹣+i D．﹣﹣i2．已知集合A={x|（x﹣1）2≤3x﹣3，x∈R}，B={y|y=3x+2，x∈R}，则A∩B=（）A．（2，+∞）B．（4，+∞）C．[2，4]D．（2，4]3．甲、乙两类水果的质量（单位：kg）分别服从正态分布N（μ1，σ12）及N（μ2，σ22），其正态分布的密度曲线如图所示，则下列说法错误的是（）A．乙类水果的质量服从的正态分布的参数σ2=1.99B．甲类水果的质量比乙类水果的质量更集中C．甲类水果的平均质量μ1=0.4kgD．甲类水果的平均质量比乙类水果的平均质量小4．已知数列{a n}的前n项和S n满足S n+S m=S n（n，m∈N*）且a1=5，则a8=（）+mA．40 B．35 C．12 D．55．设a=（），b=（），c=ln，则a，b，c的大小关系是（）A．a＞b＞c B．b＞a＞c C．b＞c＞a D．a＞c＞b6．执行如图所示的程序框图，则输出b的值为（）A．2 B．4 C．8 D．167．若圆C：x2+y2﹣2x+4y=0上存在两点A，B关于直线l：y=kx﹣1对称，则k的值为（）A．﹣1 B．﹣C．﹣D．﹣38．某同学在运动场所发现一实心椅子，其三视图如图所示（俯视图是圆的一部分及该圆的两条互相垂直的半径，有关尺寸如图，单位：m），经了解，建造该类椅子的平均成本为240元/m3，那么该椅子的建造成本约为（π≈3.14）（）A．94.20元 B．240.00元C．282.60元D．376.80元9．当函数f（x）=sinx+cosx﹣t（t∈R）在闭区间[0，2π]上，恰好有三个零点时，这三个零点之和为（）A．B． C． D．2π10．有5位同学排成前后两排拍照，若前排站2人，则甲不站后排两端且甲、乙左右相邻的概率为（）A．B．C．D．11．某工厂拟生产甲、乙两种实销产品．已知每件甲产品的利润为0.4万元，每件乙产品的利润为0.3万元，两种产品都需要在A，B两种设备上加工，且加工一件甲、乙产品在A，B设备上所需工时（单位：h）分别如表所示．甲产品所需工时乙产品所需工时A设备23B设备41若A设备每月的工时限额为400h，B设备每月的工时限额为300h，则该厂每月生产甲、乙两种产品可获得的最大利润为（）A．40万元B．45万元C．50万元D．55万元12．若函数g（x）满足g（g（x））=n（n∈N）有n+3个解，则称函数g（x）为“复合n+3解”函数．已知函数f（x）=（其中e是自然对数的底数，e=2.71828…，k∈R），且函数f（x）为“复合5解”函数，则k的取值范围是（）A．（﹣∞，0）B．（﹣e，e）C．（﹣1，1）D．（0，+∞）二、填空题（共4小题，每小题5分，满分20分）13．在Rt△ABC中，D是斜边AB的中点，若BC=6，CD=5，则•=．14．有下列四个命题：①垂直于同一条直线的两条直线平行；②垂直于同一条直线的两个平面平行；③垂直于同一平面的两个平面平行；④垂直于同一平面的两条直线平行．其中正确的命题有（填写所有正确命题的编号）．15．若等比数列{a n}的公比为2，且a3﹣a1=2，则++…+=．16．设抛物线C：y2=2px（p＞0）的焦点为F，点A在C上，若|AF|=，以线段AF为直径的圆经过点B（0，1），则p=．三、解答题（共5小题，满分60分）17．在△ABC中，设内角A，B，C所对边分别为a，b，c，且sin（A﹣）﹣cos（A+）=．（1）求角A的大小；（2）若a=，sin2B+cos2C=1，求△ABC的面积．18．某大学有甲、乙两个图书馆，对其借书、还书的等待时间进行调查，得到下表：甲图书馆12345借（还）书等待时间T1（分钟）频数1500 1000 500 500 1500乙图书馆12345借（还）书等待时间T2（分钟）频数100050020001250250以表中等待时间的学生人数的频率为概率．（1）分别求在甲、乙两图书馆借书的平均等待时间；（2）学校规定借书、还书必须在同一图书馆，某学生需要借一本数学参考书，并希望借、还书的等待时间之和不超过4分钟，在哪个图书馆借、还书更能满足他的要求？19．如图所示，在Rt△ABC中，AC⊥BC，过点C的直线VC垂直于平面ABC，D、E分别为线段VA、VC上异于端点的点．（1）当DE⊥平面VBC时，判断直线DE与平面ABC的位置关系，并说明理由；（2）当D、E、F分别为线段VA、VC、AB上的中点，且VC=2BC时，求二面角B ﹣DE﹣F的余弦值．20．已知椭圆+=1（a＞b＞0）过点P（2，1），且离心率为．（Ⅰ）求椭圆的方程；（Ⅱ）设O为坐标原点，在椭圆短轴上有两点M，N满足=，直线PM、PN分别交椭圆于A，B．（i）求证：直线AB过定点，并求出定点的坐标；（ii）求△OAB面积的最大值．21．已知函数f（x）=lnx﹣2ax（其中a∈R）．（Ⅰ）当a=1时，求函数f（x）的图象在x=1处的切线方程；（Ⅱ）若f（x）≤1恒成立，求a的取值范围；（Ⅲ）设g（x）=f（x）+x2，且函数g（x）有极大值点x0，求证：x0f（x0）+1+ax02＞0．请考生在22、23题中任选一题作答，如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22．在直角坐标系xOy中，双曲线E的参数方程为（θ为参数），设E的右焦点为F，经过第一象限的渐进线为l．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．（1）求直线l的极坐标方程；（2）设过F与l垂直的直线与y轴相交于点A，P是l上异于原点O的点，当A，O，F，P四点在同一圆上时，求这个圆的极坐标方程及点P的极坐标．[选修4-5：不等式选讲]23．已知函数f（x）=|x+a|﹣2a，其中a∈R．（1）当a=﹣2时，求不等式f（x）≤2x+1的解集；（2）若x∈R，不等式f（x）≤|x+1|恒成立，求a的取值范围．参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．解：∵z（1﹣i）2=1+i，∴，故选：C．2．解：集合A={x|（x﹣1）2≤3x﹣3，x∈R}={x|（x﹣1）（x﹣4）≤0}={x|1≤x ≤4}=[1，4]；B={y|y=3x+2，x∈R}={y|y＞2}=（2，+∞），则A∩B=（2，4]．故选：D．3．解：由图象可知，甲类水果的平均质量μ1=0.4kg，乙类水果的平均质量μ2=0.8kg，故B，C，D正确；乙类水果的质量服从的正态分布的参数σ2=，故A 不正确．故选：A．4．解：数列{a n}的前n项和S n满足S n+S m=S n+m（n，m∈N*）且a1=5，令m=1，则S n+1=S n+S1=S n+5．可得a n+1=5．则a8=5．故选：D．5．解：b=（）=＞（）=a＞1，c=ln＜1，∴b＞a＞c．故选：B．6．解：第一次循环，a=1≤3，b=2，a=2，第二次循环，a=2≤3，b=4，a=3，第三次循环，a=3≤3，b=16，a=4，第四次循环，a=4＞3，输出b=16，故选：D．7．解：圆C：x2+y2﹣2x+4y=0的圆心（1，﹣2），若圆C：x2+y2﹣2x+4y=0上存在两点A，B关于直线l：y=kx﹣1对称，可知直线经过圆的圆心，可得﹣2=k﹣1，解得k=﹣1．故选：A．8．解：由三视图可知：该几何体为圆柱的．∴体积V=．∴该椅子的建造成本约为=×240≈282.60元．故选：C．9．解：f（x）=2sin（x+）﹣t，令f（x）=0得sin（x+）=，做出y=sin（x+）在[0，2π]上的函数图象如图所示：∵f（x）在[0，2π]上恰好有3个零点，∴=sin=，解方程sin（x+）=得x=0或x=2π或x=．∴三个零点之和为0+2π+=．故选：B．10．解：由题意得：p===，故选：B．11．C解：设甲、乙两种产品月的产量分别为x，y件，约束条件是目标函数是z=0.4x+0.3y由约束条件画出可行域，如图所示的阴影部分由z=0.4x+0.3y，结合图象可知，z=0.4x+0.3y在A处取得最大值，由可得A（50，100），此时z=0.4×50+0.3×100=50万元，故选：C．12．解：函数f（x）为“复合5解“，∴f（f（x））=2，有5个解，设t=f（x），∴f（t）=2，∵当x＞0时，f（x）=，∴f（x）=，当0＜x＜1时，f′（x）＜0，函数f（x）单调递减，当x＞1时，f′（x）＞0，函数f（x）单调递增，∴f（x）min=f（1）=1，∴t≥1，∴f（t）=2在[1，+∞）有2个解，当x≤0时，f（x）=kx+3，函数f（x）恒过点（0，3），当k≤0时，f（x）≥f（0）=3，∴t≥3∵f（3）=＞2，∴f（t）=2在[3，+∞）上无解，当k＞0时，f（x）≤f（0）=3，∴f（t）=2，在（0，3]上有2个解，在（∞，0]上有1个解，综上所述f（f（x））=2在k＞0时，有5个解，故选：D二、填空题（共4小题，每小题5分，满分20分）13．解：在Rt△ABC中，D是斜边AB的中点，若BC=6，CD=5，可得AD=BD=5，即AB=10，由勾股定理可得AC==8，则•=﹣•=﹣||•||•cosA=﹣5×8×=﹣32．14．解：如图在正方体ABCD﹣A′B′C′D′中，对于①，AB⊥BB′，BC⊥BB′，AB、BC不平行，故错；对于②，两底面垂直于同一条侧棱，两个底面平面平行，故正确；对于③，相邻两个侧面同垂直底面，这两个平面不平行，故错；对于④，平行的侧棱垂直底面，侧棱平行，故正确．故答案为：②④15．解：∵等比数列{a n}的公比为2，且a3﹣a1=2，∴=2，解得a1=．∴a n==．∴=．则++…+=3×==1﹣．故答案为：1﹣．16．解：由题意，可得A（，），AB⊥BF，∴（，﹣1）•（，﹣1）=0，∴﹣+1=0，∴p（5﹣p）=4，∴p=1或4．三、解答题（共5小题，满分60分）17．解：（1）sin（A﹣）﹣cos（A+）=sin（A﹣）﹣cos（2π﹣A）=sin（A﹣）﹣cos（A+）=sinA﹣cosA﹣cosA﹣sinA=即cosA=，∵0＜A＜π，∴A=．（2）由sin2B+cos2C=1，可得sin2B=2sin2C，由正弦定理，得b2=2c2，即．a=，cosA==，解得：c=1，b=∴△ABC的面积S=bcsinA=．18．解：（1）根据已知可得T1的分布列：T1（分钟）12345P0.30.20.10.10.3T1的数学期望为：E（T1）=1×0.3+2×0.2+3×0.1+4×0.1+5×0.3=2.9．T2（分钟）12345P0.20.10.4 0.250.05T2的数学期望为：E（T1）=1×0.2+2×0.1+3×0.4+4×0.25+5×0.05=2.85．因此：该同学甲、乙两图书馆借书的平均等待时间分别为：2.9分钟，2.85分钟．（2）设T11，T12分别表示在甲图书馆借、还书所需等待时间，设事件A为“在甲图书馆借、还书的等待时间之和不超过4分钟”．T11+T12≤4的取值分别为：（1，1），（1，2），（1，3），（2，1），（2，2），（3，1）．。

2018年山东省实验中学高考数学一模试卷（理科）一、选择题（本大题共12小题．每小题5分．共60分．在每小题给出的四个选项中．只有一项是符合题目要求的．）1．（5分）设集合A＝{x|y＝log2（2﹣x）}，B＝{x|x2﹣3x+2＜0}，则∁A B＝（）A．（﹣∞，1）B．（﹣∞，1]C．（2，+∞）D．[2，+∞）2．（5分）复数+z对应的点的坐标为（2，﹣2），则z在复数平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．（5分）已知向量＝（x，1），＝（1，﹣2），且⊥，则|+|＝（）A．B．C．D．104．（5分）已知双曲线my2﹣x2＝1（m∈R）与抛物线x2＝8y有相同的焦点，则该双曲线的渐近线方程为（）A．y＝±x B．y＝±x C．y＝±x D．y＝±3x 5．（5分）宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n＝（）A．5B．4C．3D．26．（5分）已知，则（）A．b＜a＜c B．a＜b＜c C．c＜b＜a D．c＜a＜b 7．（5分）某几何体的三视图如图所示，则它的最长棱长是（）A．2B．C．D．38．（5分）函数g（x）＝2cos（x﹣）cos（x+）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变）后得到h（x）的图象，设f（x）＝x2+h（x），则f′（x）的图象大致为（）A．B．C．D．9．（5分）如果的展开式中各项系数的和为16，则展开式中x3项的系数为（）A．B．C．D．10．（5分）已知三棱锥P﹣ABC的各顶点都在同一球面上，且P A⊥平面ABC，若该棱锥的体积为，AB＝2，AC＝1，∠BAC＝60°，则此球的表面积等于（）A．5πB．20πC．8πD．16π11．（5分）已知A，B是过抛物线y2＝2px（p＞0）焦点F的直线与抛物线的交点，O是坐标原点，且满足|的值为（）A．B．C．4D．212．（5分）已知偶函数f（x）满足f（4+x）＝f（4﹣x），且当x∈（0，4]时，f （x）＝，关于x的不等式f2（x）+af（x）＞0在[﹣200，200]上有且只有200个整数解，则实数a的取值范围是（）A．B．C．D．二、填空题（本题共4小题，每小题5分，共20分.）13．（5分）已知实数x，y满足约束条件，则z＝3x+y的最小值为．14．（5分）在平面区域{（x，y）|0≤x≤2，0≤y≤4}内投入一点P，则点P的坐标（x，y）满足y≤x2的概率为．15．（5分）在△ABC中，，过B点作BD⊥AB交AC于点D．若AB ＝CD＝1，则AD＝．16．（5分）已知函数f（x）＝a sin（πωx+φ）（a≠0，ω＞0，|φ|≤），直线y＝a与f（x）的图象的相邻两个交点的横坐标分别是2和4，现有如下命题：①该函数在[2，4]上的值域是[a，a]；②在[2，4]上，当且仅当x＝3时函数取最大值；③该函数的最小正周期可以是；④f（x）的图象可能过原点．其中的真命题有（写出所有真命题的序号）．三、解答题（共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.）（一）必考题：60分.17．（12分）已知数列{a n}满足：．（I）令，求证：数列{b n}为等比数列并求数列{a n}的通项公式；（II）令c n＝na n，S n为数列{c n}的前n项和，求证：S n＜2．18．（12分）在刚刚过去的济南市第一次模拟考试中，某班同学表现优异，成绩突出，现将全班50名同学的成绩按班内名次统计成如下的2×2列联表：（I ）完成列联表，若定义前20名的学生为优等生，能否在犯错误的概率不超过0.1的前提下，认为该班“成绩是否优等与性别有关”？请说明理由． 附：．（II ）优等生中的男生成绩在学校前100名的只有2人，现从这8人中抽取3人，记其中成绩在学校前100名的人数为ξ，求ξ的分布列及数学期望． 19．（12分）已知四棱锥P ﹣ABCD ，PD ⊥面ABCD 且PD ＝2，△BCD 是边长为的正三角形，AB ＝AD ，∠BAD ＝120°，M 为PC 上的点，且．（I ）求证：P A ∥面MBD ；（II ）求二面角M ﹣BD ﹣P 的余弦值．20．（12分）已知椭圆的左，右焦点分别为F 1、F 2，过焦点且垂直于长轴的弦长为3．过左焦点的直线l 与椭圆交于A ，B 两点，M 是AB 的中点．（I ）求椭圆的标准方程；若直线l 不平行于坐标轴，证明：直线OM （O 是坐标原点）与直线l的斜率之积为定值；（II）D是椭圆上一点（A，D在x轴的同侧），且满足l∥DF2，求四边形AF1F2D 面积的最大值．21．（12分）已知函数f（x）＝e x+ax﹣a（a≠0）．（I）函数f（x）不存在零点，求实数a的范围；（II）若f'（x）为函数f（x）的导函数，对任意与的大小关系，并给出证明．（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.[选修4-4，坐标系与参数方程]（10分）22．（10分）在平面直角坐标系xOy中直线l的倾斜角45°，且经过点P（1，﹣1），以坐标系xOy的原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线E的极坐标方程为ρ＝4cosθ，直线l与曲线E相交于A，B两点．（I）求直线l的一般方程和曲线E的标准方程；（II）求的值．[选修4-5，不等式选讲]（10分）23．已知定义在R上的函数f（x）＝|x﹣2m|﹣|x|m∈N*，且f（x）＜4恒成立．（I）解关于x的不等式f（x）＞1﹣3x；（II）若．2018年山东省实验中学高考数学一模试卷（理科）参考答案与试题解析一、选择题（本大题共12小题．每小题5分．共60分．在每小题给出的四个选项中．只有一项是符合题目要求的．）1．（5分）设集合A＝{x|y＝log2（2﹣x）}，B＝{x|x2﹣3x+2＜0}，则∁A B＝（）A．（﹣∞，1）B．（﹣∞，1]C．（2，+∞）D．[2，+∞）【解答】解：A＝{x|y＝log2（2﹣x）}＝{x|x＜2}，B＝{x|x2﹣3x+2＜0}＝{x|1＜x＜2}，则∁A B＝{x|x≤1}，故选：B．2．（5分）复数+z对应的点的坐标为（2，﹣2），则z在复数平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：设z＝x+yi，+z＝+x+yi＝﹣+x+yi＝x+（y﹣1）i，∴x＝2，y﹣1＝﹣2，∴x＝2，y＝﹣1，∴z在复数平面内对应的点为（1，﹣1），故选：D．3．（5分）已知向量＝（x，1），＝（1，﹣2），且⊥，则|+|＝（）A．B．C．D．10【解答】解：由题意可得＝（x，1）•（1，﹣2）＝x﹣2＝0，解得x＝2．再由+＝（x+1，﹣1）＝（3，﹣1），可得|+|＝，故选：B．4．（5分）已知双曲线my2﹣x2＝1（m∈R）与抛物线x2＝8y有相同的焦点，则该双曲线的渐近线方程为（）A．y＝±x B．y＝±x C．y＝±x D．y＝±3x【解答】解：∵抛物线x2＝8y的焦点为（0，2），∴双曲线的一个焦点为（0，2），∴+1＝4，∴m＝，∴双曲线的渐近线方程为y＝±x．故选：A．5．（5分）宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n＝（）A．5B．4C．3D．2【解答】解：当n＝1时，a＝，b＝4，满足进行循环的条件，当n＝2时，a＝，b＝8满足进行循环的条件，当n＝3时，a＝，b＝16满足进行循环的条件，当n＝4时，a＝，b＝32不满足进行循环的条件，故输出的n值为4，故选：B．6．（5分）已知，则（）A．b＜a＜c B．a＜b＜c C．c＜b＜a D．c＜a＜b【解答】解：∵，∴a＝log0.8（log3π）＜log0.81＝0，＝log（log316）＜log0.8（log3π）＜log0.81＝0，0.8c＝＞＝log0.81＝0．∴b＜a＜c．故选：A．7．（5分）某几何体的三视图如图所示，则它的最长棱长是（）A．2B．C．D．3【解答】解：画出三视图定义的几何体的直观图，如图：PC＝2，P A＝＝3，AC＝AB＝，BC＝2，所以最长的棱长为：P A：3．故选：D．8．（5分）函数g（x）＝2cos（x﹣）cos（x+）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变）后得到h（x）的图象，设f（x）＝x2+h（x），则f′（x）的图象大致为（）A．B．C．D．【解答】解：∵g（x）＝2cos（x﹣）cos（x+）＝cos2x，∴将函数g（x）的图象上各点的坐标伸长为原来的2倍（纵坐标不变）后得到h （x）＝cos x的图象，∴f（x）＝x2+h（x）＝x2+cos x，可得：f′（x）＝x﹣sin x，∴可得：f′（﹣x）＝（﹣x）﹣sin（﹣x）＝﹣（x﹣sin x）＝﹣f′（x），故此函数奇函数，排除B，D．又当x＝﹣时，f′（0）＝﹣+1＝1﹣＞0，结合选项函数的图象，排除C．故选：A．9．（5分）如果的展开式中各项系数的和为16，则展开式中x3项的系数为（）A．B．C．D．【解答】解：展开式中，令x＝1得展开式中各项系数的和为（a﹣）•（1+1）6＝16，解得a＝1；∴（x﹣）（x+）6，又（x+）6的展开式通项公式为T r+1＝•x6﹣r•＝•x6﹣2r，由6﹣2r＝2，解得r＝2，∴（x+）6展开式中含x2的系数为＝15；令6﹣2r＝4，解得r＝1，∴（x+）6展开式中含x4的系数为＝6；∴（x﹣）（x+）6展开式中x3项的系数为1×15﹣×6＝．故选：D．10．（5分）已知三棱锥P﹣ABC的各顶点都在同一球面上，且P A⊥平面ABC，若该棱锥的体积为，AB＝2，AC＝1，∠BAC＝60°，则此球的表面积等于（）A．5πB．20πC．8πD．16π【解答】解：由题意，AB＝2，AC＝1，∠BAC＝60°，余弦定理可得：cos∠BAC＝解得：BC＝可得S ABC＝AB•AC sin60°＝．△ABC外接圆的半径r，则2r＝∴r＝1∵P A⊥平面ABC，棱锥的体积为，那么：P A＝h＝＝4．可得：球的半径R＝＝．那么球的表面积S＝4πR2＝20π．故选：B．11．（5分）已知A，B是过抛物线y2＝2px（p＞0）焦点F的直线与抛物线的交点，O是坐标原点，且满足|的值为（）A．B．C．4D．2【解答】解：不妨设直线AB的斜率k＞0，过A，B作抛物线准线的垂线，垂足分别为C，D，过B作BE⊥AC于E，由满足，可得丨AC丨＝2丨BD丨，∴E为AC的中点，即丨AE丨＝丨AB丨，∴丨BE丨＝＝丨AB丨，＝S OAF+S OBF＝丨BE丨•丨OF丨＝p丨AB丨，由S△OABS△OAB＝丨AB丨，∴丨AB丨＝p丨AB丨，即p＝2，由丨AE丨＝丨AB丨，则直线AB斜率为k AB＝±2，直线AB的方程y＝2（x﹣1），，整理得：2x2﹣5x﹣2＝0，则x1+x2＝，则丨AB丨＝x1+x2+p＝+2＝，故选：A．12．（5分）已知偶函数f（x）满足f（4+x）＝f（4﹣x），且当x∈（0，4]时，f （x）＝，关于x的不等式f2（x）+af（x）＞0在[﹣200，200]上有且只有200个整数解，则实数a的取值范围是（）A．B．C．D．【解答】解：当0＜x≤4时，f′（x）＝，令f′（x）＝0得x＝，∴f（x）在（0，）上单调递增，在（，4）上单调递减，∵f（x）是偶函数，∴f（x+4）＝f（4﹣x）＝f（x﹣4），∴f（x）的周期为8，作出f（x）一个周期内的函数图象如图所示：∵f（x）是偶函数，且不等式f2（x）+af（x）＞0在[﹣200，200]上有且只有200个整数解，∴不等式在（0，200）内有100个整数解，∵f（x）在（0，200）内有25个周期，∴f（x）在一个周期（0，8）内有4个整数解，（1）若a＞0，由f2（x）+af（x）＞0，可得f（x）＞0或f（x）＜﹣a，显然f（x）＞0在一个周期（0，8）内有7个整数解，不符合题意；（2）若a＜0，由f2（x）+af（x）＞0，可得f（x）＜0或f（x）＞﹣a，显然f（x）＜0在区间（0，8）上无解，∴f（x）＞﹣a在（0，8）上有4个整数解，∵f（x）在（0，8）上关于直线x＝4对称，∴f（x）在（0，4）上有2个整数解，∵f（1）＝ln2，f（2）＝＝ln2，f（3）＝，∴f（x）＞﹣a在（0，4）上的整数解为x＝1，x＝2．∴≤﹣a＜ln2，解得﹣ln2＜a≤﹣．故选：C．二、填空题（本题共4小题，每小题5分，共20分.）13．（5分）已知实数x，y满足约束条件，则z＝3x+y的最小值为．【解答】解：由实数x，y满足约束条件作出可行域如图，联立，解得A（，），化目标函数z＝3x+y为y＝﹣3x+z，由图可知，当直线y＝﹣3x+z过A时，直线在y轴上的截距最小，z有最小值为3×+＝．故答案为：．14．（5分）在平面区域{（x，y）|0≤x≤2，0≤y≤4}内投入一点P，则点P的坐标（x，y）满足y≤x2的概率为．【解答】解：平面区域{（x，y）|0≤x≤2，0≤y≤4}的面积为2×4＝8．区域内满足y≤x2如图阴影部分，其面积S＝，则在平面区域{（x，y）|0≤x≤2，0≤y≤4}内投入一点P，点P的坐标（x，y）满足y≤x2的概率为．故答案为：．15．（5分）在△ABC中，，过B点作BD⊥AB交AC于点D．若AB＝CD＝1，则AD＝．【解答】解：设AD＝x，且BD⊥AB，AB＝CD＝1，在△BCD中，，则，且sin∠BDC＝sin（π﹣∠ADB）＝sin∠ADB＝＝，由正弦定理得，，所以BC＝＝＝，在△ABC中，由余弦定理得，AC2＝AB2+BC2﹣2•AB•BC cos∠ABC则，化简得，则x4+2x3＝2x+4，即x3（x+2）＝2（x+2），解得x＝，即AD＝，故答案为：．16．（5分）已知函数f（x）＝a sin（πωx+φ）（a≠0，ω＞0，|φ|≤），直线y＝a与f（x）的图象的相邻两个交点的横坐标分别是2和4，现有如下命题：①该函数在[2，4]上的值域是[a，a]；②在[2，4]上，当且仅当x＝3时函数取最大值；③该函数的最小正周期可以是；④f（x）的图象可能过原点．其中的真命题有④（写出所有真命题的序号）．【解答】解：当a＝﹣1时，函数f（x）＝a sin（πωx+φ）化为f（x）＝﹣sin（πωx+φ），该函数在[2，4]上的值域是[﹣，﹣1]，故①错误；在[2，4]上，当且仅当x＝3时函数取最小值，故②错误；由周期公式T＝＝，得，此时f（x）＝a sin（x+φ），由，解得sinφ＝cosφ＝﹣，不满足|φ|≤，可知该函数的最小正周期不可以是，故③错误；由f（0）＝φ＝0，得sinφ＝0，即φ＝0（|φ|≤），故④正确．∴正确命题的序号是④．故答案为：④．三、解答题（共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.）（一）必考题：60分.17．（12分）已知数列{a n}满足：．（I）令，求证：数列{b n}为等比数列并求数列{a n}的通项公式；（II）令c n＝na n，S n为数列{c n}的前n项和，求证：S n＜2．【解答】证明：（Ⅰ）数列{a n}满足：．所以＝＝＝2（常数），所以数列{b n}是以＝2为首项，2为公比的等比数列．所以，整理得：，当n＝1时，符合通项，故：，n∈N*．（Ⅱ），则：，设数列{}的前n项和为T n故：①，②，①﹣②得：，解得，由于数列{}的前n项和S n＜数列{}的前n项和T n，故S n＜2．18．（12分）在刚刚过去的济南市第一次模拟考试中，某班同学表现优异，成绩突出，现将全班50名同学的成绩按班内名次统计成如下的2×2列联表：（I ）完成列联表，若定义前20名的学生为优等生，能否在犯错误的概率不超过0.1的前提下，认为该班“成绩是否优等与性别有关”？请说明理由． 附：． （II ）优等生中的男生成绩在学校前100名的只有2人，现从这8人中抽取3人，记其中成绩在学校前100名的人数为ξ，求ξ的分布列及数学期望． 【解答】解：（1）由题意可得列联表：由列联表得，K 2＝≈3.463∈（2.706，3.841）．因为，所以在犯错误的概率不超过0.1的前提下，认为该班“成绩是否优等与性别有关”．（2）ξ的可能取值为0，1，2．P （ξ＝0）＝＝．P （ξ＝1）＝＝，P （ξ＝2）＝＝．所以的分布列为Eξ＝0×+1×+2×＝．19．（12分）已知四棱锥P﹣ABCD，PD⊥面ABCD且PD＝2，△BCD是边长为的正三角形，AB＝AD，∠BAD＝120°，M为PC上的点，且．（I）求证：P A∥面MBD；（II）求二面角M﹣BD﹣P的余弦值．【解答】证明：（Ⅰ）取BD中点O，则AO⊥BD，CO⊥BD，进而A、O、C共线，……………………（1分）由已知得AB＝2，OA＝1，OC＝3，所以AO＝，又PM＝，所以OM∥P A，……………………………………………………………（3分）又P A⊄面MBD，OM⊂面MBD，所以P A∥面MBD．…………………………………………………………（5分）解：（Ⅱ）过O作PD的平行线l，因为PD⊥面ABCD，所以l⊥面ABCD，所以l⊥AC，l⊥BD，分别以OB，OC，l所在直线为x轴，y轴，z轴建立如图所示空间直角坐标系．…………………………………………………………（6分）因为B（），D（﹣），C（0，3，0），P（），所以＝（2，0，0），因为PM＝，所以，3＝（，，），设＝（x，y，z）是平面MBD的一个法向量，则，不妨令y＝1，则＝（0，1，3），………………………………………………（9分）＝（0，1，0）是面PBD的一个法向量，……………………………………………………（10分）设二面角M﹣BD﹣P的大小为θ，所以cosθ＝＝，即二面角M﹣BD﹣P的余弦值为．……………………………………………………（12分）20．（12分）已知椭圆的左，右焦点分别为F1、F2，过焦点且垂直于长轴的弦长为3．过左焦点的直线l与椭圆交于A，B两点，M 是AB的中点．（I）求椭圆的标准方程；若直线l不平行于坐标轴，证明：直线OM（O是坐标原点）与直线l的斜率之积为定值；（II）D是椭圆上一点（A，D在x轴的同侧），且满足l∥DF2，求四边形AF1F2D 面积的最大值．【解答】解：（Ⅰ）∵过焦点且垂直于长轴的弦长为3，∴＝＝3，得b＝，所求椭圆的标准方程是+＝1；设A（x1，y1），B（x2，y2），M（x0，y0），可得x1+x2＝2x0，y1+y2＝2y0，又+＝1，+＝1，相减可得+＝0，即有k AB＝＝﹣＝﹣，即有直线OM与直线l的斜率之积为定值﹣；（Ⅱ）椭圆的焦点为F1（﹣1，0），F2（1，0），设直线l：x＝my﹣1，代入椭圆方程3x2+4y2＝12，可得（4+3m2）y2﹣6my﹣9＝0，设A（x1，y1），B（x2，y2），可得y1+y2＝，y1y2＝﹣，延长DF2交椭圆与点E，连接BE，根据对称性，可得S＝S ABED＝S＝•2c•|y1﹣y2|△＝|y1﹣y2|＝＝＝12，可令t＝，则m2＝t2﹣1，（t≥1），可得12＝12•＝，由3t+在t≥1递增，可得3t+的最小值为4，可得t＝1即m＝0时，四边形AF1F2D面积取得最大值3．21．（12分）已知函数f（x）＝e x+ax﹣a（a≠0）．（I）函数f（x）不存在零点，求实数a的范围；（II）若f'（x）为函数f（x）的导函数，对任意与的大小关系，并给出证明．【解答】解：（I）函数f（x）不存在零点，即为e x+ax﹣a＝0无实数解，由于x＝1时，e+0＝0显然不成立．若x≠1，即有﹣a＝，令g（x）＝，则g′（x）＝，当x＞2时，g′（x）＞0，g（x）递增，当x＜1和1＜x＜2时，g′（x）＜0，g（x）递减．即有x＝2处g（x）取得极小值，为e2，在x＜1时，g（x）＜0，则0＜﹣a＜e2，解得﹣e2＜a＜0，则实数a的取值范围为（﹣e2，0）．（II）f′（x）＝e x+a，∴＝+a．＝＝+a．∴﹣＝﹣＝．令t＝x2﹣x1＞0，则g（t）＝t﹣e t+1，g′（t）＝（1+﹣），令h（x）＝1+x﹣e x（x＞0），h′（x）＝1﹣e x＜0，∴h（x）＜h（0）＝0．∴g′（t）＜0，∴g（t）＜g（0）＝0．∴＜．（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.[选修4-4，坐标系与参数方程]（10分）22．（10分）在平面直角坐标系xOy中直线l的倾斜角45°，且经过点P（1，﹣1），以坐标系xOy的原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线E的极坐标方程为ρ＝4cosθ，直线l与曲线E相交于A，B两点．（I）求直线l的一般方程和曲线E的标准方程；（II）求的值．【解答】解（1）由题意可知直线l的倾斜角45°，且经过点P（1，﹣1），所以直线的方程为y+1＝x﹣1，整理得x﹣y﹣2＝0．曲线E的极坐标方程为ρ＝4cosθ，转换为直角坐标方程为x2+y2＝4x，转换为标准方程为：（x﹣2）2+y2＝4，（2）根据题意把直线x﹣y﹣2＝0，转换为参数方程为（t为参数），将其代入曲线E方程，可得．所以t 1•t2＝﹣2，（t1和t2为A和B对应的参数），所以＝．[选修4-5，不等式选讲]（10分）23．已知定义在R上的函数f（x）＝|x﹣2m|﹣|x|m∈N*，且f（x）＜4恒成立．（I）解关于x的不等式f（x）＞1﹣3x；（II）若．【解答】解：（Ⅰ）定义在R上的函数f（x）＝|x﹣2m|﹣|x|m∈N*，且f（x）＜4，可得：|x﹣2m|﹣|x|≤|2m|＜4，则|m|＜2，解得﹣2＜m＜2．又m∈N*，∴m＝1．定义在R上的函数f（x）＝|x﹣2|﹣|x|＝，所以当x＞2时，﹣2＞1﹣3x解得x＞1，所以x＞2，当0≤x≤2时，2﹣2x＞1﹣3x，解得0≤x≤2，当x＜0时，2＞1﹣3x，解得0＞x，综上可得，不等式的解集为：{x|﹣}，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）（Ⅱ）证明：∵α∈（0，1），β∈（0，1），∴f（α）+f（β）＝2﹣2α+2﹣2β＝3，即，∴＝2（）（α+β）＝2（5+）＝18，当且仅当，即，时取等号，故≥18．。

山东省实验中学20l5级第三次诊断性测试理科综合试题（2017．12)注意事项:1．答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

可能用到元素的相对原子质量：H 1 C12 O 16 Na 23 Ca 40 Cu 64一、选择题：本题共13个小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在细胞分化过程中，一般不会发生的变化是A．细胞的形态B．细胞的结构C．细胞的功能D．细胞的数量2．氰化物是一种剧毒物质，进入机体后能迅速与细胞色素氧化酶的三价铁离子结合，抑制该酶活性，导致[H]和O2不能结合而使细胞陷入内窒息状态.如图为研究植物根尖吸收钾离子的相关实验。

下列分析不正确的是A．细胞色素氧化酶位于线粒体内膜B．加入氰化物后，细胞对氧气的吸收速率不变C．实验甲可以判断植物根尖细胞吸收K+属于主动运输D．实验乙中，4h后吸收K+的能量可能来自于无氧呼吸3．下列有关生物进化的叙述，错误的是A．有性生殖的出现实现了基因重组，明显加快了生物进化的速度B．无论是自然选择还是人工选择，都能使种群基因频率发生定向改变C．古老地层中没有复杂生物的化石，而新近地层中可能有简单生物的化石D．共同进化的生物之间不存在地理隔离，因此共同进化不能形成新的物种4．下列有关神经递质的叙述，错误的是A．神经冲动引起神经递质的释放，实现了由电信号向化学信号的转变B．神经递质必须与突触后膜上的受体结合,才能改变突触后膜的膜电位C．当肾上腺素作为神经递质发挥作用时,该生命活动的调节方式为神经—体液调节D．如果神经递质发挥作用后不及时失活，反射的准确性和适应性就会受到影响5．如图，为某家系遗传系谱图，已知I2患白化病，III3患红绿色盲症，如果IV1两对基因均为显性结合的概率是9/16，那么需要满足以下哪项条件？A．II5、III1均不携带相关致病基因B．II5、III1均携带相关致病基因C．II4、II5携带白化病基因、III1不携带白化病基因D．III携带白化病基因，III2白化病、红绿色盲症基因均携带6．大多数生物的翻译起始密码子为AUG或GUG.在下图所示的某mRNA部分序列中,若下划线表示的是该mRNA上一个决定谷氨酸的密码子，则该部分序列(无终止密码子）翻译出来的肽段所含的氨基酸的个数为A．6 B．8 C．9 D．10化学变化的是7．下列描述不涉及．．．A．铁粉作袋装食品的抗氧化剂B．二氧化硫作纸浆的漂白剂C．氢氟酸作普通玻璃的刻蚀剂D．利用渗析实验除去淀粉溶液中的NaC18．阿伏加德罗常数的值为N A，下列说法正确的是A．标准状况下，22。

山东省实验中学2012级第三次诊断性考试理科综合试题2018．12 说明：试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为第1页至第6页，第Ⅱ卷为第7页至第16页。

试题答案请用2B铅笔或0.5mm签字笔填涂到答题卡规定位置上，书写在试题上的答案无效。

考试时间150分钟。

可能用到的相对原子质量：:H1 D 2 C 12 N 14 O 16 Mg 24 Al 27 S 32 Fe 56 Cu 64第Ⅰ卷（共107分）一、选择题（本题共13小题，每小题5分，共65分。

每小题只有一个选项．．．．．．符合题意）1．内质网与核膜、细胞膜相连，这种结构特点表明内质网的重要功能之一是A．扩展细胞内膜，有利于酶的附着 B．提供细胞内物质运输的通道C．提供核糖体附着的支架D．参与细胞内某些代谢反应2.下面的数学模型能表示的生物学含义是A．人体红细胞中K+吸收速率随O2浓度变化的情况B．萌发的种子中自由水含量随时间变化的情况C．酶促反应速率随底物浓度变化的情况D．Aa的个体自交后代中纯合子所占比例随自交次数增加的情况3．以下有关实验的叙述正确的是A．观察植物细胞有丝分裂的操作步骤：取材→解离→染色→漂洗→压片→观察B．在观察质壁分离与复原的实验中需要用显微镜观察两次细胞形态C．蛋白质鉴定：将适量的双缩脲试剂A液和B液混合→滴加到豆浆样液中→观察D．用黑藻叶片进行观察质壁分离与复原实验时，叶绿体的存在不会干扰实验现象的观察4．下图为人体部分细胞的生命历程示意图，图中①～⑩为不同的细胞，a～f表示细胞所进行的生理过程。

据图分析，下列叙述正确的是A．在成熟的生物体中，细胞的自然更新是通过a和f过程完成的B．④⑤⑥⑦⑨的核基因相同，细胞内的蛋白质种类和数量不相同C．d过程的细胞内染色质固缩，核体积缩小D．e过程的细胞不会发生细胞凋亡且细胞周期会延长5．下面左图为细胞分裂过程中细胞核内DNA 含量变化的曲线图，右图表示是某二倍体雄性动物的一个细胞示意图。

山东省实验中学高三测试 数学（理科）第Ⅰ卷一、选择题（共12题，每题只有一个正确答案，每题5分，共60分） 1. 设复数（a+i ）2对应的点在y 轴负半轴上，则实数a 的值是3.2.1.1.---D C B A2. 若log a 2<log b 2<0，则A.0<a<b <1B.0<b<a <1 C .a>b >1 D.b>a >13. 各项均为实数的等比数列{a n }的前n 项之和为S n ，若S 10=10,S 30=70则S 40等于 A.150 B.-200 C.150或-200 D.400或-1504. 若,6,log 6),3()(2⎩⎨⎧≥<+=x x x x f x f 则f (-1)的值为 A.1 B.2 C.3 D.45. 在空间中，给出下面五个命题① 过平面α外的两点,有且只有一个平面与平面α垂直； ② 若平面β内有不共线三点到平面α的距离都相等，则α∥β ③ 若直线l 与平面内的无数条直线垂直，则l ⊥α;④ 两条异面直线在同一平面内的射影一定是两条平行； ⑤ 点P 到正三角形ABC 的三条边的距离相等，则三棱锥P-ABC 为正三棱锥以上命题正确的个数是A.0B.1C.2D.36. 函数y=f (x )的曲线如图所示，那么函数y=f (2-x )的曲线是7. 在（1+3x ）n 和（2x+5）n 的展开式中各项系数之和分别为a n ,b n , n 为正数，则所有，在双曲线上，若的两个焦点，是双曲线、设）条件是（的一个充分不必要则设非空集合0)0,0(1.996.9.96.91.},)22)(3({},5312{.83.21.2.31.432lim 21222221=⋅>>=-≤≤≤<<≤≤⋂⊆--==-≤≤+==--→PF PF P b a by a x F F a D a C a B a A B A A x x y x B a x a x A D C B A b a b a nn nn xn，则双曲线的离心率为为半焦距)(2c ac =215.2.213.213.++-D C B A 为止，若试，到区分出所有次品件不同次品一一进行测件不同正品和对某种产品的46.10所有次品恰好在第五次测试被全部发现，则这样的测试方法有（ ）种 A.24 B.96 C.576 D.72011.已知关于x 的方程sin 2x +cos x +k =0有实数解，则实数k 的取值范围是145.145.145.45.<<-≤≤-<≤--≥k D k C k B k A 12.若直线y=kx+1与圆x 2+y 2+kx +my -4=0交于M ，N 两点，且M ，N 关于直线x-y =0对称，动点P （a,b ）在不等式组⎪⎩⎪⎨⎧≥≤-≥+-0002y m y kx y kx 表示的平面区域内部及边界上运动，则12--=a b w 的取值范围是 [)(](][)+∞⋃-∞---∞-+∞,22,.]2,2.[2,.,2.D C B A13.抛物线y=ax 2(a ≠0)的 焦点坐标为 . 14.设随机变量ξ的概率分布列为P （ξ=k ）=)1(+k k c,k =1,2,3,4.其中c 为常数,则P）（2521<<ξ的值为. 15.如图△ABC 中，G 为重心，PQ 过G 点，=m ,=n 则=+nm 11 . 16.在120°的二面角内放入一个表面积为36π的球，使球与这两个半平面各有且只有一个公共点，那么这两点之间的球面距离等于 .三、解答题（本题共6小题74分，应写出必要的文字说明，证明过程或演算步骤） 17.（12分）已知向量m =(sin B ,1-co sB )，且与向量n=(2,0)所成角为3π，其中A ，B ，C 是ΔABC 的内角.（1）求角B 的大小；（2）求sin A +sin C 的取值范围.18(12分)如图是一个方格迷宫，甲、乙两人分别位于迷宫A 、B 两处，现以每分钟一格的速度同时出发，在每个路口只能向东、西、南、北四个方向之一行走。

山东省实验中学2018-2019学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 双曲线E 与椭圆C ：x 29＋y 23＝1有相同焦点，且以E 的一个焦点为圆心与双曲线的渐近线相切的圆的面积为π，则E 的方程为（ ） A.x 23－y 23＝1 B.x 24－y 22＝1 C.x 25－y 2＝1 D.x 22－y 24＝1 2． 已知函数[)[)1(1)sin 2,2,212()(1)sin 22,21,222nn x n x n n f x x n x n n ππ+⎧-+∈+⎪⎪=⎨⎪-++∈++⎪⎩（n N ∈），若数列{}m a 满足*()()m a f m m N =∈，数列{}m a 的前m 项和为m S ，则10596S S -=（ ） A.909 B.910 C.911 D.912【命题意图】本题考查数列求和等基础知识，意在考查分类讨论的数学思想与运算求解能力. 3． 在平面直角坐标系中，直线y=x 与圆x 2+y 2﹣8x+4=0交于A 、B 两点，则线段AB 的长为（ ） A ．4 B ．4C ．2D ．24． 已知命题:()(0xp f x a a =>且1)a ≠是单调增函数；命题5:(,)44q x ππ∀∈，sin cos x x >.则下列命题为真命题的是（ ）A ．p q ∧B ．p q ∨⌝ C. p q ⌝∧⌝ D ．p q ⌝∧ 5． 已知三棱锥S ABC -外接球的表面积为32π，090ABC ∠=，三棱锥S ABC -的三视图如图 所示，则其侧视图的面积的最大值为（ ）A ．4 B． C ．8 D．6． 已知空间四边形ABCD ，M 、N 分别是AB 、CD 的中点，且4AC =，6BD =，则（ ） A ．15MN << B ．210MN << C ．15MN ≤≤ D ．25MN << 7． 若某程序框图如图所示，则该程序运行后输出的值是（ ） A.7B.8C. 9D. 10【命题意图】本题考查阅读程序框图，理解程序框图的功能，本质是循环语句循环终止的条件.8． 过抛物线22(0)y px p =>焦点F 的直线与双曲线2218-=y x 的一条渐近线平行，并交其抛物线于A 、 B 两点，若>AF BF ，且||3AF =，则抛物线方程为（ ）A ．2y x =B ．22y x =C ．24y x =D ．23y x =【命题意图】本题考查抛物线方程、抛物线定义、双曲线标准方程和简单几何性质等基础知识，意在考查方程思想和运算能力．9． 命题“∀a ∈R ，函数y=π”是增函数的否定是（ ）A ．“∀a ∈R ，函数y=π”是减函数B ．“∀a ∈R ，函数y=π”不是增函数C ．“∃a ∈R ，函数y=π”不是增函数D ．“∃a ∈R ，函数y=π”是减函数10．已知函数()xF x e =满足()()()F x g x h x =+，且()g x ，()h x 分别是R 上的偶函数和奇函数， 若(0,2]x ∀∈使得不等式(2)()0g x ah x -≥恒成立，则实数的取值范围是（ ）A ．(,-∞B ．(,-∞C ．(0,D ．)+∞ 11．如图所示，在三棱锥P ABC -的六条棱所在的直线中，异面直线共有（ ）111]A ．2对B ．3对C ．4对D ．6对12．已知M N 、为抛物线24y x =上两个不同的点，F 为抛物线的焦点．若线段MN 的中点的纵坐标为2，||||10MF NF +=，则直线MN 的方程为（ ）A ．240x y +-=B ．240x y --=C ．20x y +-=D ．20x y --=二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知()f x 为定义在R 上的偶函数，当0x ≥时，()22x f x =-，则不等式()16f x -≤的解集 是 ▲ ．14．定义在R 上的函数)(x f 满足：1)(')(>+x f x f ，4)0(=f ，则不等式3)(+>xxe xf e （其 中为自然对数的底数）的解集为 .15．已知()212811f x x x -=-+,则函数()f x 的解析式为_________.16．某种产品的加工需要 A ，B ，C ，D ，E 五道工艺，其中 A 必须在D 的前面完成（不一定相邻），其它工艺的顺序可以改变，但不能同时进行，为了节省加工时间，B 与C 必须相邻，那么完成加工该产品的不同工艺的排列顺序有 种．（用数字作答）三、解答题（本大共6小题，共70分。