广东2011年中考数学试题分类解析汇编专题9：三角形

广东2012年中考数学试题分类解析汇编 专题9：三角形 一、选择题 1. （2012广东广州3分）在Rt△ABC 中，∠C=90°，AC=9，BC=12，则点C 到AB 的距离是【 】A ．B ．C ．D ．【答案】A 。

【考点】勾股定理，点到直线的距离，三角形的面积。

【分析】根据题意画出相应的图形，如图所示。

在Rt△ABC 中，AC=9，BC=12，根据勾股定理得：2222AB=AC +BC 9+1215==。

过C 作CD⊥AB，交AB 于点D ，则由S △ABC =12AC•BC=12AB•CD，得AC BC 91236CD AB 155⋅⨯===。

∴点C 到AB 的距离是365。

故选A 。

2. （2012广东深圳3分）小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为300，同一时 刻，一根长为l 米、垂直于地面放置的标杆在地面上的影长为2米，则树的高度为【 】A.(63)+米B.12米C.(423)+米 D ．10米【答案】A 。

【考点】解直角三角形的应用（坡度坡角问题），锐角三角函数定义，特殊角的三角函数值，相似三角形的判定和性质。

【分析】延长AC交BF延长线于E点，则∠CFE=30°。

作CE⊥BD于E，在Rt△CFE中，∠CFE=30°，CF=4，∴CE=2，EF=4cos30°=23，在Rt△CED中，CE=2，∵同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米，∴DE=4。

∴BD=BF+EF+ED=12+23。

∵△DCE∽△DAB，且CE：DE=1：2，∴在Rt△ABD中，AB=12BD=()112+236+32=。

故选A。

3. （2012广东深圳3分）如图，已知：∠MON=30o，点A1、A2、A3在射线ON上，点B1、B2、B3…．．在射线OM上，△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形，若OA1=l，则△A6B6A7的边长为【】A．6 B．12 C．32 D．64【答案】C。

广东2011年中考数学试题分类解析汇编专题9：三角形一、选择题1. （茂名3分）如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，若DE=5，则BC=A 、6B 、8C 、10D 、12【答案】C 。

【考点】三角形中位线定理。

【分析】利用三角形的中位线定理求得BC 即可。

故选C 。

2.（茂名3分）如图，已知：45°＜A ＜90°，则下列各式成立的是 A 、sinA=cosA B 、sinA ＞cosAC 、sinA ＞tanAD 、sinA ＜cosA【答案】B 。

【考点】锐角三角函数的定义，三角形的边角关系。

【分析】∵45°＜A ＜90°，∴BC ＞AC 。

而sinA=BC AB ，cosA=ACAB ，∴sinA ＞cosA 。

又∵C=900，∴AB ＞BC ＞AC 。

而tanA=BCAC，∴sinA ＜tanA 。

故选B 。

3.（深圳3分）如图，小正方形边长均为1，则下列图形中三角形(阴影部分)与△ABC 相似的是【答案】B 。

【考点】相似三角形的判定。

【分析】如B图△EFG和△ABC中，∠EFG=∠ABC=1350，AB 2CB 22 , 2 EF 1GF 2====，AB CB EF GF∴=。

EFG ABC ∴∆∆∽。

实际上， A ，C ，D 三图中三角形最大角都小于∠ABC ，即可排它，选B 即可。

4.（深圳3分）如图，△ABC 与△DEF 均为等边三角形，O 为BC 、EF 的中点，则AD ：BEA.3:1 B. 2:1 C.5:3 D.不确定【答案】A 。

【考点】等边三角形的性质，相似三角形的判定和性质。

【分析】连接AO ，DO 。

设等边△ABC 的边长为a ，等边△ABC 的边长为b 。

∵O 为BC 、EF 的中点，∴AO 、DO 是BC 、EF 的中垂线。

∴∠AOC=∠DOC=900，∴∠AOD=1800—∠COE 。

点关注，每天更新全国各区真题详解版和经典中考题型、考点、知识点2011年广东省中考数学试卷参考答案与试题解析一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑. 1．（3分）﹣2的倒数是（ ） A ． 2 B ． ﹣2 C ． D．考点： 难度： M112 倒数 容易题． 分析： 这道题需要我们清楚倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．而以上四个选项中，只有﹣2×（）=1，所以﹣2的倒数是﹣．其余均选项不符合提议。

故选D 解答： D ．点评：本题主要考查倒数的概念及性质，属于中考的一个高频考点，倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数2．（3分）据中新社北京2010年12月8日电，2010年中国粮食总产量达到546400000吨，用科学记数法表示为（ ）A ． 5.464×107吨B ． 5.464×108吨C ． 5.464×109吨D ． 5.464×1010吨考点： 难度： M11C 科学记数法 容易题．分析： 首先我们要知道，什么是科学计数法：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．那么本题中将546400000用科学记数法可表示为5.464×108．故选B解答： B ．点评： 本题我们需要注意科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．3．（3分）将下图中的箭头缩小到原来的，得到的图形是（ ）A ．B．C．D ．考点：难度：M32I 相似图形的应用 容易题．分析：本题需要我们根据相似图形的定义，并且结合图形，然后对选项一一分析，即可排除错误答案．∵图中的箭头要缩小到原来的，∴箭头的长、宽都要缩小到原来的；选项B箭头大小不变；选项C箭头扩大；选项D的长缩小、而宽没变．故选A解答：A．点评：本题较简单，主要考查了相似图形的定义，注意：即两个图形的形状相同，但大小不一定相同的变换就是相似变换．4．（3分）在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（）A ．B．C．D．考点：难度：M222 概率的计算容易题．分析：解决本题，我们需要先求出所有球的个数与红球的个数，然后再根据概率公式便可求出答案．即，共8球在袋中，其中5个红球，故摸到红球的概率为，故选C.解答：C．点评：这道题需要掌握概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=，难度适中．5．（3分）正八边形的每个内角为（）A ．120°B．135°C．140°D．144°考点：难度：M331 多边形的内（外）角和中等题．分析：此题我们要根据正多边形的内角求法，得出每个内角的表示方法，便可求出答案．即：[（n﹣2）×180]÷n=[（8﹣2）×180]÷8=135°，故选B解答：B．点评：本题主要考查了多边形的内（外）角和，属于中考中频考点，注意正n边形的内角ɑ=[（n﹣2）×180]÷n.正确的记忆正多边形的内角求法公式是解决问题的关键．二、填空题（本大题5小题，每小题4分，共20分）请将下列各题的正确答案填写在答题卡相应的位置上. 6．(4分)已知反比例函数解析式的图象经过（1，﹣2），则k=．考点：难度：M137 用待定系数法求函数关系式容易题．分析：根据待定系数法，将（1﹣2）代入式即可得出k的值．具体解法如下：∵反比例函数解析式的图象经过（1，﹣2），∴k=xy=﹣2，解答： ﹣2．点评：本题比较简单，考查了用待定系数法求反比例函数的解析式，属于中考高频考点，对以此类题型只需要将已知点带入函数即可求出答案。

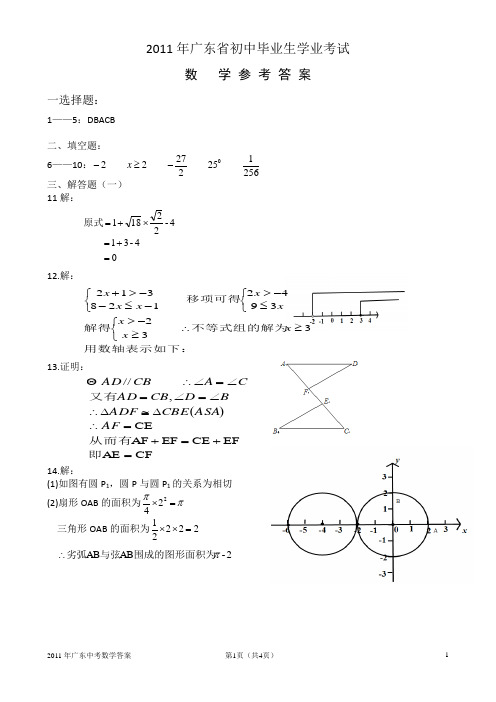
2011年广东省初中毕业生学业考试数 学 参 考 答 案一选择题：1——5：DBACB二、填空题：6——10：256125227220-≥-x 三、解答题（一）11解：4-314-22181=+=⨯+=原式 12.解： 用数轴表示如下：不等式组的解为解得移项可得3323942128312≥∴⎩⎨⎧≥->⎩⎨⎧≤->⎩⎨⎧-≤-->+x x x xx x x x 13.证明：()CF AE EFCE EF AF CE,//=+=+=∴∆≅∆∴∠=∠=∠=∠∴即从而有又有AF ASA CBE ADF BD CB AD CA CB AD14.解：(1)如图有圆P 1，圆P 与圆P 1的关系为相切(2)扇形OAB 的面积为ππ=⨯224三角形OAB 的面积为22221=⨯⨯ 2-AB AB π围成的图形面积为与弦劣弧∴（1）由于抛物线与x 轴没有交点2121412>∴<⨯⨯-=∆∴c c（2）显然）经过点（直线1,01+=cx y ，又由(1)知21>c如图，直线1+=cx y 只能够在21l l 和之间∴直线经过一、二、三象限附：显然直线经过点（0,1）和点（0,1c -） 又01021<-∴>>c c连接点（0,1）和点（0,1c -）可以知道直线经过一、二、三象限四、解答题（二）16.解：设该箱饮料一箱有x 瓶，依题意有：()()10,10)(131001013013036.0326262=∴=∴-==∴=-+∴=-+=+-x x x x x x x x x x 意义代入分式方程可知它有不符合题意，舍去或通分化简的17.解：设AD=x()()m x x x BD CD BC x AD ADACD ADCD xADAD ABD AD BD CDADACD BD ADABD 3.681325135050333330t an t an 145t an t an t an ,t an 00≈+⨯=-=∴=-=-=∴===∠====∠=∴=∠=∠(1)此次调查的总体是李老师班上的50名学生(2)如图(3)路上时间花费在30分钟以上（含30分钟）的人数占全班人数的百分比是%10%1005014=⨯+ 19.解： (1)0301=∠=∠∴=C CFBF 000090303-180BDF 30C 12=⨯=∠∴=∠=∠=∠又 (2)0302BDF RT )1(=∠∆，知有由63c o s BD AB 3021903BAD RT 342cos 00=∠==∠-∠-=∠∆=∴∠∙=∴中，在BD BF BD五、解答题（三）20、解：（1）15864 （2）122222-+-n n n n（3）()()()12112222222-+-=-⨯++-n n n n n n n 21.解： （1）始终与AGC ∆相似的三角形有：HGA ∆∆和HAB（2）HAB AGC ∆∆~1）知由（x y y x HB AC AB CG 8199=∴==∴即 （3）HGA ~AGC 1∆∆）知由（()不是菱形四边形中在时，、当为菱形四边形中在时、当或解得即为平行四边形，只要要使得四边形显然）（即可以得到代入直线将）（即代入抛物线可得将即显然的函数关系式为直线的代入直线将即有得令得代入直线将即有得令对于抛物线的函数关系式为设直线BCMN 5CP MP CM RT 1,2)2,2(M 22BCMN BC25CP MP CM RT 2,23)23,1(,11212541545BC MN BCMN //NM )3()30(41545121141745121,M 121AB 141745,N 141745)0,(P ,OP )2(121AB 21AB B ),25B(3,,25,31AB A ,1,0A ,1,0141745AB )1(2222222222∴≠=+=∆==∴=∴==+=∆==∴====+-==∴≤≤+-=∴--++-==∴++==++-++-===+=∴======++-=+=BCMPC CP MP t MPC CP MP M t t t t t s BCt t t s t t t MN s t t t y t x t t t t t y t x t t x y a y x b y x x x y bax y。

2011年广东省中考数学试卷2011年广东省中考数学试卷一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.1．（2011•孝感）﹣2的倒数是（）A．2 B．﹣2 C．D．2．（2011•广东）据中新社北京2010年12月8日电，2010年中国粮食总产量达到546400000吨，用科学记数法表示为（）A．5.464×107吨B．5.464×108吨C．5.464×109吨D．5.464×1010吨3．（2011•广东）将下图中的箭头缩小到原来的，得到的图形是（）A．B．C．D．4．（2011•广东）在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（）A．B．C．D．5．（2011•广东）正八边形的每个内角为（）A．120°B．135°C．140°D．144°二、填空题（本大题5小题，每小题4分，共20分）请将下列各题的正确答案填写在答题卡相应的位置上.6．（2011•广东）已知反比例函数解析式的图象经过（1，﹣2），则k=_________．7．（2011•广东）使在实数范围内有意义的x的取值范围是_________．8．（2011•广东）按下面程序计算：输入x=3，则输出的答案是_________．9．（2011•广东）如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C=_________．10．（2011•广东）如图（1），将一个正六边形各边延长，构成一个正六角星形AFBDCE，它的面积为1，取△ABC 和△DEF各边中点，连接成正六角星形A1F1B1D1C1E1，如图（2）中阴影部分，取△A1B1C1和△D1E1F1各边中点，连接成正六角星形A2F2B2D2C2E2，如图（3）中阴影部分，如此下去…，则正六角星形A4F4B4D4C4E4的面积为_________．三、解答题（一）（本大题5小题，每小题6分，共30分）11．（2011•广东）计算：．12．（2011•广东）解不等式组，并把解集在数轴上表示出来．13．（2011•广东）已知：如图，E、F在AC上，AD∥CB且AD=CB，∠D=∠B．求证：AE=CF．14．（2011•广东）如图，在平面直角坐标系中，点P的坐标为（﹣4，0），⊙P的半径为2，将⊙P沿x轴向右平移4个单位长度得⊙P1（1）画出⊙P1，并直接判断⊙P与⊙P1的位置关系；（2）设⊙P1与x轴正半轴，y轴正半轴的交点分别为A、B．求劣弧与弦AB围成的图形的面积（结果保留π）15．（2011•广东）已知抛物线与x轴没有交点．（1）求c的取值范围；（2）试确定直线y=cx+1经过的象限，并说明理由．四、解答题（二）（本大题4小题，每小题7分，共28分）16．（2011•广东）某品牌瓶装饮料每箱价格26元，某商店对该瓶装饮料进行“买一送三”促销活动，即整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元，问该品牌饮料一箱有多少瓶？17．（2011•广东）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路，现新修一条路AC到公路l，小明测量出∠ACD=30°，∠ABD=45°，BC=50m，请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：≈1.414，≈1.732）18．（2011•广东）李老师为了解班里学生的作息时间，调查了班上50名学生上学路上花费的时间，他发现学生所花时间都少于50分钟，然后将调查数据整理，作出如下频数分布直方图的一部分（每组数据含最小值不含最大值）．请根据该频数分布直方图，回答下列问题：（1）此次调查的总体是什么？（2）补全频数分布直方图；（3）该班学生上学路上花费时间在30分钟以上（含30分钟）的人数占全班人数的百分比是多少？19．（2011•广东）如图，直角梯形纸片ABCD中，AD∥BC，∠A=90°，∠C=30°，折叠纸片使BC经过点D，点C落在点E处，BF是折痕，且BF=CF=8．（1）求∠BDF的度数；（2）求AB的长．五、解答题（三）（本大题3小题，每小题9分，共27分）20．（2011•广东）如下数表是由从1开始的连续自然数组成，观察规律并完成各题的解答．（1）表中第8行的最后一个数是_________，它是自然数_________的平方，第8行共有_________个数；（2）用含n的代数式表示：第n行的第一个数是_________，最后一个数是_________，第n行共有_________个数；（3）求第n行各数之和．21．（2011•广东）如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=AC=EF=9，∠BAC=∠DEF=90°，固定△ABC，将△DEF绕点A顺时针旋转，当DF边与AB边重合时，旋转中止．现不考虑旋转开始和结束时重合的情况，设DE，DF（或它们的延长线）分别交BC（或它的延长线）于G，H点，如图（2）（1）问：始终与△AGC相似的三角形有_________及_________；（2）设CG=x，BH=y，求y关于x的函数关系式（只要求根据图（2）的情形说明理由）；（3）问：当x为何值时，△AGH是等腰三角形．22．（2011•广东）如图，抛物线y=﹣x2+x+1与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）（1）求直线AB的函数关系式；（2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N．设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；（3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN 为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由．2011年广东省中考数学试卷参考答案与试题解析一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.1．（2011•孝感）﹣2的倒数是（）A．2 B．﹣2 C．D．考点：倒数。

2011年中考数学真题分类汇编(第二十九章锐角三角函数与特殊角—含答案)D【答案】B3. （2011四川内江，11，3分）如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=4，CE=43，则△ABC的面积为A．83B．15 C．93D．123【答案】C4. （2011山东临沂，13，3分）如图，△ABC中，cosB＝22，sinC＝53，则△ABC的面积是（）A．221B．12 C．14 D．21【答案】A5. （2011安徽芜湖，8，4分）如图，直径为10BACDE的⊙A 经过点C (0,5)和点O (0,0)，B 是y 轴右侧⊙A 优弧上一点,则∠OBC 的余弦值为( ). A ．12B ．34C ．32D ．45【答案】C6. （2011山东日照，10，4分）在Rt △ABC 中，∠C =90°，把∠A 的邻边与对边的比叫做∠A 的余切，记作cot A =a b ．则下列关系式中不成．．立．的是（ ）（A ）tan A ·cot A =1 （B ）sin A =tan A ·cos A（C）cos A=cot A·sin A（D）tan2A+cot2A=1【答案】D7. （2011山东烟台，9,4分）如果△ABC中，sin A=cos B=2，则下列最确切的结论是（）A. △ABC是直角三角形B.△ABC是等腰三角形C. △ABC是等腰直角三角形D.△ABC是锐角三角形【答案】C8. (2011 浙江湖州，4，3)如图，已知在Rt△ABC中，∠C＝90°，BC＝1，AC=2，则tan A的值为A．2 B．1C．52D．255【答案】B9. （2011浙江温州，5，4分）如图，在△ABC中，∠C=90°，AB＝13，BC＝5，则sin A的值是( )A．513B．1213C．512D．135【答案】A10．（2011四川乐山2，3分）如图，在4×4的正方形网格中，tanα=A．1 B．2 C．12D．5【答案】B11. （2011安徽芜湖，8,4分）如图，直径为10的⊙A经过点C(0,5)和点O (0,0)，B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为( ).A．12B．34C．32D．45【答案】B12. （2011湖北黄冈，9，3分）cos30°=（）A．12B．22C．32D．3【答案】C13. （2011广东茂名，8，3分）如图，已知：9045<<A，则下列各式成立的是A．sinA＝cosA B．sinA>cosAC．sinA>tanA D．sinA<cosA【答案】B14. (20011江苏镇江,6,2分)如图,在Rt△ABC中，∠ACB=90°,CD⊥AB,垂足为 D.若5则sin∠ACD的值为( )5 25 C. 5 D. 23答案【 A 】15. （2011湖北鄂州，9，3分）cos30°=（ ）A ．12B ．22C ．32D 3【答案】C16. （2011湖北荆州，8，3分）在△ABC 中，∠A ＝120°，AB ＝4，AC ＝2，则B sin 的值是A ．1475B ．53C ．721D ．1421 【答案】D17. （2011湖北宜昌，11，3分）如图是教学用直角三角板，边AC=30cm ，∠C=90°，tan ∠BAC=33,则边BC 的长为( ). A. 303cm B. 203cm C.103cm D. 53cm【答案】C二、填空题1. （2011江苏扬州，13,3分）如图，C岛在A岛的北偏东60°方向，在B岛的北偏西45°方向，则从C岛看A、B两岛的视角∠ACB=【答案】105°2. （2011山东滨州，16，4分）在等腰△ABC 中，∠C=90°则tanA=________.【答案】13. （2011江苏连云港，14，3分）如图，△ABC 的顶点都在方格纸的格点上，则sin A=_______.【答案】124. （ 2011重庆江津， 15，4分）在Rt △ABC 中,∠C=90º,BC=5,AB=12,sinA=_________.【答案】125·5. （2011江苏淮安，18，3分）如图，在Rt △ABC 中，∠ABC=90°，∠ACB=30°，将△ABC 绕点A 按逆时针方向旋转15°后得到△AB 1C 1，B 1C 1交AC 于点D ，如果AD=，则△ABC 的周长等于 .【答案】66. (2011江苏南京，11，2分)如图，以O 为圆心，任意长为半径画弧，与射线OM 交于点A ，再以A 为圆心，AO 长为半径画弧，两弧交于点B ，画射线OB ，则cos ∠AOB 的值等于_________．(第11B A M O【答案】127. （2011江苏南通，17，3分）如图，测量河宽AB（假设河的两岸平行），在C点测得∠ACB ＝30°，D点测得∠ADB＝60°，又CD＝60m，则河宽AB为▲ m（结果保留根号）.【答案】303.8. （2011湖北武汉市，13，3分）sin30°的值为_____．【答案】129. (20011江苏镇江,11,2分)∠α的补角是120°,则∠α=______,sinα=______.答案:60°，310．（2011贵州安顺，14，4分）如图，点E(0，4)，O(0，0)，C(5，0)在⊙A上，BE是⊙A上的一条弦，则tan∠OBE= ．第14题【答案】54三、解答题(1) 1. （2011安徽芜湖，17（1），6分）计算：2011315(1)()(cos68)338sin 602π---+++-. 【答案】 解：解: 原式18138=--++ …………………………………4分8=-…………………………………6分 2. （2011四川南充市，19，8分）如图，点E 是矩形ABCD 中CD 边上一点，⊿BCE 沿BE 折叠为⊿BFE,点F 落在AD 上. (1)求证：⊿ABE ∽⊿DFE;(2)若sin ∠DFE=31,求tan ∠EBC 的值.FED CBA【答案】（1）证明：∵四边形ABCD 是矩形∴∠A=∠D=∠C=90° ∵⊿BCE 沿BE 折叠为⊿BFE ∴∠BFE=∠C=90°∴∠AFB+∠DFE=180°-∠BFE=90°又∠AFB+∠ABF=90° ∴∠ABF=∠DFE ∴⊿ABE ∽⊿DFE(2)解：在Rt ⊿DEF 中，sin ∠DFE=EF DE =31∴设DE=a,EF=3a,DF=22DE EF -=22a∵⊿BCE 沿BE 折叠为⊿BFE ∴CE=EF=3a,CD=DE+CE=4a,AB=4a, ∠EBC=∠EBF又由（1）⊿ABE ∽⊿DFE ，∴BF FE =AB DF =a a 422=22∴tan ∠EBF=BF FE =22tan ∠EBC=tan ∠EBF=223. （2011甘肃兰州，21，7分）已知α是锐角，且sin(α+15°)=2。

(2012年1月最新最细）2011全国中考真题解析120考点汇编☆相似三角形判定和性质一、选择题1.（2011湖北荆州，7，3分）如图，P为线段AB上一点，AD与BC交干E，∠CPD=∠A=∠B，BC交PD于E，AD交PC于G，则图中相似三角形有（）A、1对B、2对C、3对D、4对考点：相似三角形的判定．专题：证明题．分析：根据题目提供的相等的角和图形中隐含的相等的角，利用两对应角对应相等的两三角形相似找到相似三角形即可．解答：解：∵∠CPD=∠A=∠B，∴△PCF∽△BCP△APG∽△BFP△APD∽△GPD故选B．点评：本题考查相似三角形的判定．识别两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边、对应角．2.（2011江苏无锡，7，3分）如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形．若OA：OC=0B：OD，则下列结论中一定正确的是（）A．①与②相似B．①与③相似 C．①与④相似D．②与③相似考点：相似三角形的判定。

分析：由OA：OC﹣=0B：OD，利用对顶角相等相等，两三角形相似，①与③相似，问题可求．解答：证明：∵OA：OC=0B：OD，∠AOB=∠COD（对顶角相等），∴①与③相似．故选B．点评：本题解答的关键是熟练记住所学的三角形相似的判定定理，此题难度不大，属于基础题．3.（2011山西，11，2分）如图，△ABC中，AB＝AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形．若DE＝2㎝，则AC的长为（）A． B．4cm C． D．考点：三角形中位线，相似三角形的相似比专题：相似三角形分析：由题意知DE 是等腰△ABC 的中位线，所以DE ∥BC ，DE ＝12BC ， 因为DE ＝2㎝，所以BC ＝4㎝．又DE ∥BC ， 所以△ADE ∽△ABC ，且相似比为12．过点A 作AM ⊥BC 于点M ．则MC ＝2㎝， 由点E 是边AC 的中点，EF ∥AM ，所以FC ＝1㎝．在△EFC 中， 因为正方形DEFG 的边长是2㎝，所以根据勾股定理得ECAC＝)cm ， 故选D ．解答：D点评：此题是三角形中位线， 等腰三角形的性质，勾股定理，相似三角形的相似比等的综合应用．过点A 作AM ⊥BC 于点M ，构造等腰三角形的高学生不易想到．4. （2011陕西，9，3分）如图，在□ABCD 中，E 、F 分别是AD 、CD 边上的点，连接BE 、AF ，他们相交于点G ，延长BE 交CD 的延长线于点H ，则图中的相似三角形共有（ ）A ．2对B ．3对C ．4对D ．5对考点：相似三角形的判定；平行四边形的性质。

2011年广东省初中毕业生学业考试数 学考试用时100分钟，满分为120分一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．－2的倒数是（ ）A ．2B ．－2C ． 21D ．21- 2．据中新社北京2010年12月8日电，2010年中国粮食总产量达到546 400 000吨，用科学记数法表示为（ ）A ．5.464×107吨B ．5.464×108吨C ．5.464×109吨D ．5.464×1010吨3．将左下图中的箭头缩小到原来的1，得到的图形是（ ） 4．在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（ ）A ．51B ．31C ．85D ．83 5．正八边形的每个内角为（ ）A ．120ºB ．135ºC ．140ºD ．144º二、填空题（本大题5小题，每小题4分，共20分）请将下列各题的正确答案填写在答题卡相应的位置上．6．已知反比例函数xk y =的图象经过(1，－2)，则=k ____________． 7．使2-x 在实数范围内有意义的x 的取值范围是______ _____．8．按下面程序计算：输入3=x ，则输出的答案是_______________．9．如图，AB 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ．若∠A =40º，则∠C =_____．10．如图(1)，将一个正六边形各边延长，构成一个正六角星形AFBDCE ，它的面积为1；取△ABC 和△DEF各边中点，连接成正六角星形A 1F 1B 1D 1C 1E 1，如图(2)中阴影部分；取△A 1B 1C 1和△D 1E 1F 1各边中点，连接成正六角星形A 2F 2B 2D 2C 2E 2，如图(3)中阴影部分；如此下去…，则正六角星形A 4F 4B 4D 4C 4E 4的面积为A ．B ． D ． 题3图 题9图 BC O A_________________．三、解答题（一）（本大题5小题，每小题6分，共30分）11．计算：20245sin 18)12011(-︒+-．12．解不等式组：⎩⎨⎧-≤-->+128,312x x x ，并把解集在数轴上表示出来．13．已知：如图，E 14．如图，在平面直角坐标系中，点P 的坐标为（－4，0），⊙P 的半径为2，将⊙P 沿x 轴向右平移4个单位长度得⊙P 1．（1）画出⊙P 1，并直接判断⊙P 与⊙P 1的位置关系；（2）设⊙P 1与x 轴正半轴，y 轴正半轴的交点分别为A ，B ，求劣弧AB 与弦AB 围成的图形的面积（结果保留π）．15．已知抛物线c x x y ++=221与x 轴没有交点． （1）求c 的取值范围；（2）试确定直线1+=cx y 经过的象限，并说明理由．四、解答题（二）（本大题4小题，每小题7分，共28分）16．某品牌瓶装饮料每箱价格26元．某商店对该瓶装饮料进行“买一送三”促销活动，若整箱购买，则题13图 B C DA F E 题14图题10图（1） E E C E 题10图（2） 题10图（3）买一箱送三瓶，这相当于每瓶比原价便宜了0.6元．问该品牌饮料一箱有多少瓶？17．如图，小明家在A 处，门前有一口池塘，隔着池塘有一条公路l ，AB 是A 到l 的小路. 现新修一条路AC 到公路l . 小明测量出∠ACD =30º，∠ABD =45º，BC =50m . 请你帮小明计算他家到公路l 的距离AD 的长度（精确到0.1m ；参考数据：414.12≈，732.13≈）.18．李老师为了解班里学生的作息时间表，调查了班上50名学生上学路上花费的时间，他发现学生所花时间都少于50分钟，然后将调查数据整理，作出如下频数分布直方图的一部分（每组数据含最小值不含最大值）．请根据该频数分布直方图，回答下列问题：（1）此次调查的总体是什么？（2）补全频数分布直方图；（3）该班学生上学路上花费时间在30分钟以上（含30分钟）的人数占全班人数的百分比是多少？19．如图，直角梯形纸片ABCD 中，AD //BC ，∠A =90º，∠C =30º．折叠纸片使BC 经过点D ，点C 落在点E处，BF 是折痕，且BF =CF =8．（1）求∠BDF 的度数；（2）求AB 的长．五、解答题（三）（本大题3小题，每小题9分，共27分）20．如下数表是由从1开始的连续自然数组成，观察规律并完成各题的解答．12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 2526 27 28 29 30 31 32 33 34 35 36…………………………（1）表中第8行的最后一个数是______________，它是自然数_____________的平方，第8行共有____________个数；（2）用含n 的代数式表示：第n 行的第一个数是___________________，最后一个数是________________，第n 行共有_______________个数；第17题图 ) 题19图 B CED AF 题18图（3）求第n 行各数之和．21．如图（1），△ABC 与△EFD 为等腰直角三角形，AC 与DE 重合，AB =AC =EF =9，∠BAC =∠DEF =90º，固定△ABC ，将△DEF 绕点A 顺时针旋转，当DF 边与AB 边重合时，旋转中止．现不考虑旋转开始和结束时重合的情况，设DE ，DF (或它们的延长线)分别交BC (或它的延长线) 于G ，H 点，如图(2)（1）问：始终与△AGC 相似的三角形有及 ；（2）设CG =x ，BH =y ，求y 关于x 的函数关系式（只要求根据图(2)的情形说明理由）（3）问：当x 为何值时，△AGH 是等腰三角形.22．如图，抛物线1417452++-=x y 与y 轴交于A 点，过点A 的直线与抛物线交于另一点B ，过点B 作BC ⊥x （1（2）动点P 在线段OC 点M ，交抛物线于点N . 设点P 移动的时间为t 出t （3）设在（2）的条件下（不考虑点P 与点O BCMN 为平行四边形？问对于所求的t 2011一、1-5、DBACB二、6、-27、___ x ≥2__8、___12__9、__25º__ 10、2561 三、11、原式=-6 12、x ≥3 13、由△ADF ≌△CB E ，得AF =C E ，故得：AE=CF14、（1）⊙P 与⊙P 1外切。

2011年广东省初中毕业生学业考试1．21-的相反数是（ ） A ．2 B ．－2 C ．21 D ．21- 2．如图，已知AB∥CD，直线EF 分别交AB ，CD 于点E ，F ，EG 平分∠BEF ，若∠1=5O°，则∠2的度数为( )． A.50° B.55° C.60° D.65° 3．将左下图中的箭头缩小到原来的21，得到的图形是（ ）4、下列计算中，正确的是（ ）A 、xy y x 532=+B 、 3632)(y x y x -=- C 、428x x x =÷D 、()9322+=+x x5．正六边形的每个内角为（ ）A ．120ºB ．135ºC ．140ºD ．108º 6．因式分解 =-x x 283______ _________ ___ 7．使21-x 在实数范围内有意义的x 的取值范围是______ _____．8．如图，AB 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ． 若∠A =50º，则∠C =___ __． 9．按下面程序计算：输入3=x ，则输出的答案是_______________．10、如图7-①，图7-②，图7-③，图7-④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是________，第n 个“广”字中的棋子个数是________11．计算：2201221145cos 18)12012(-⎪⎭⎫ ⎝⎛-+-︒+- A ．B ．D ．题3图题8图BCO12．解不等式组：⎪⎩⎪⎨⎧-≥-->--125,121x x x x ，并把解集在数轴上表示出来．13．已知：如图，E ，F 在AC 上，AD //CB 且AD =CB ，∠D =∠B ．求证：AE =CF ．14．如图，在平面直角坐标系中，点P 的坐标为（－4⊙P 的半径为2，将⊙P 沿x 轴向右平移4（1）画出⊙P 1，直接判断⊙P 与⊙P 1的位置关系； （2）设⊙P 1与x 轴正半轴，y 轴正半轴的交点分别为A ，B ，求劣弧AB 与弦AB 围成的图形的面积（结果保留π）．15．甲、乙两人用如图所示的两个分格均匀的转盘做游戏：分别转动两个转盘，若转盘停止后，指针指向一个数字（若指针恰好停在分格线上，则重转一次），用所指的两个数字作乘积，如果积大于10，那么甲获胜；如果积不大于10，那么乙获胜。