解 从3幅画中选2幅 取分别挂在左、右 边墙,上 可以分两步: 完成 第1步 ,从 3幅画中 1幅选 挂在左 ,有 边 3种墙上 方;法 第2步,从剩下 2幅 的画中 1幅 选画挂在右 上,有2种方. 法
根据分步乘法,不 计同 数挂 原法 理种数是 N326.
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
用两个计数
原理解决计
数问题时
,最
重要的是
在
开始 计算 之
前要进 行仔
细分析
需
要分类还
是
需要分步
.
分 类 要"不 做重 到不 ".分漏 类后再分别 对 每 一 类 进,行 最计 后数 用 分 类 加 数 原 理 求 ,得和 到 总. 数
分 步 要"步 做骤 到完 ". 整完成了所有 步 骤,恰 好 完 成 任,当务然 步 与 步 之 间 要 相 互 独立.分 步 后 再 计 算 每 一方步法的 数,最 后 根 据 分 步 乘 法原计理,数把 完 成 每 一 步 方 法 数 相 ,得乘到 总 .数
新课
分类记数原理: 做一件事情,完成它可以有
n类办法,在第一类办法中有m1种不同的方法,在 第二类办法中有m2种不同的方法,……,在第 n类办法中有mn种不同的方法。那么完成这件 事共有
N=m1+m2+…+mn 种不同的方法。
分步记数原理:做一件事情,完成它需要分
成n个步骤,做第一步有m1种不同的方法,做第 二步有m2种不同的方法,……,做第n步有mn 种不同的方法,那么完成这件事有
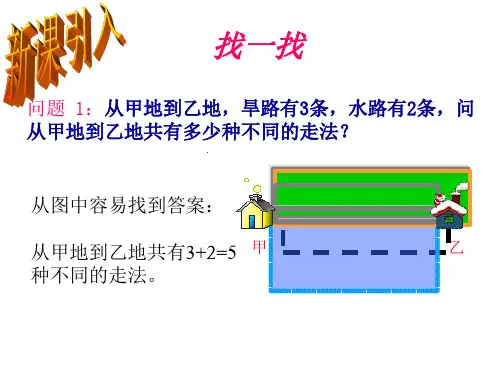
问题3:用前6个大写英文字母和1~9个阿拉伯