第3章实用计算方法

人教版数学五下第3章《长方体和正方体》（推导长正方体的体积计算方法）教案一、教学目标1.掌握长方体和正方体的定义及特点。

2.理解长方体和正方体的体积计算公式。

3.能够推导出长方体和正方体的体积计算方法。

4.进一步理解几何体的立体图形性质。

二、教学重点1.长方体和正方体的定义和特点。

2.长方体和正方体的体积计算方法。

三、教学难点1.推导长方体和正方体的体积计算方法。

2.理解长方体和正方体的关系及应用。

四、教学准备1.板书、彩色粉笔。

2.长方体和正方体的模型。

3.课件PPT。

五、教学过程第一步：导入1.引导学生回顾长方体和正方体的定义，并复习相关特点。

第二步：讲解1.讲解长方体和正方体的体积计算公式。

2.结合实际生活中的例子，说明体积计算的重要性。

第三步：推导1.提问学生如何计算长方体和正方体的体积。

2.引导学生通过立体图形的方式，推导出长方体和正方体的体积计算方法。

第四步：巩固1.给学生发放练习册，让他们在练习中巩固所学知识。

2.师生互动，解答学生在实践中遇到的问题。

第五步：拓展1.引导学生思考长方体和正方体的特殊情况，如正方体是长方体的特殊情况。

2.讨论长方体和正方体在实际生活中的应用。

六、课堂小结1.总结长方体和正方体的体积计算方法。

2.强调掌握数学知识的重要性。

七、作业布置1.完成练习册上相关习题。

2.思考长方体和正方体在日常生活中的应用场景。

八、教学反思1.教师应当注意引导学生从实际问题出发，思考数学问题的应用性与实用性。

2.教师应关注学生的学习兴趣和思维习惯，及时给予指导和帮助。

以上为人教版数学五下第3章《长方体和正方体》（推导长正方体的体积计算方法）教案，希望能帮助学生更好地理解和掌握相关知识。

第三章 化学反应动力学的计算化学反应的速度各不相同，有的反应速度极快，只要几个毫微秒就达到平衡(接近扩散速度，如无机酸碱中和)，有的反应速度极慢，几乎看不到变化(如自然界的某些变化)。

大部分有机化学反应可用常规方法测量，对某些快速反应则可用停留法、驰豫法等测量。

不论反应速度的快慢，动力学方程都是类似的。

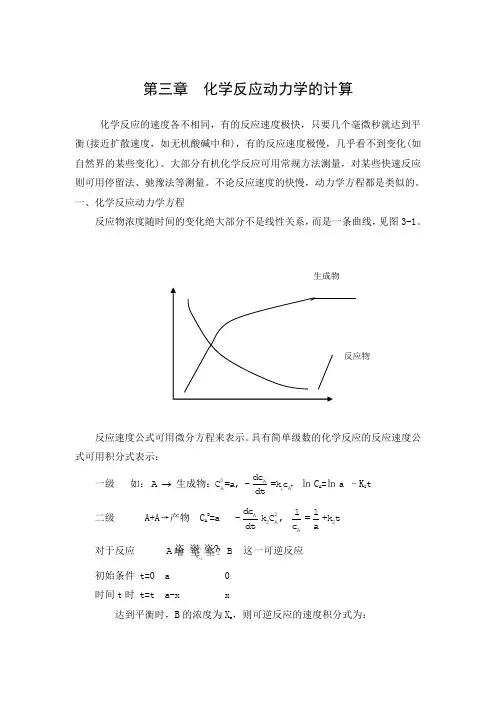
一、化学反应动力学方程反应物浓度随时间的变化绝大部分不是线性关系，而是一条曲线，见图3-1。

反应速度公式可用微分方程来表示。

具有简单级数的化学反应的反应速度公式可用积分式表示：一级 如：0AA1Adc A C =a, -=k c dt 生成物：，㏑C A =㏑a –K 1t 二级 A+A →产物 C A 0=a 2A 2A 2A d c 11-k C , =+k t d t c a对于反应 1-1k k A B 这一可逆反应初始条件 t=0 a 0 时间t 时 t=t a-x x达到平衡时，B 的浓度为X e ，则可逆反应的速度积分式为： 级数：1-1 1-10k A A e e 1A -1B k 0e 0C =a dc x xA B=-k C +k C : =kt dt a x -xC =0ln 1-21-10Ak0A e e e B 1A -1B C k e e 0CC =a dc x ax +x(a-x )A B+C C =0=-k C +k C C : =kt dt 2a-x a(x -x)C =0ln 二、常微分方程的解化学反应动力学方程是用微分方程表示的，对于简单的反应，可直接求得微分方程的解。

微分方程：()(1)(,,,......)......(1)n n y f x y y y -'=在区间a<x<b 的解，是指()y x ϕ=,这样一个函数，在所述区间内存在导数()(),(),......()n x x x ϕϕϕ'''。

且对于区间a<x<b 内的每一个x ，等式(1)都成立。

2020-2021学年五年级数学上册暑假预习与检测衔接讲义第三章小数除法【知识点归纳】1、小数除以整数的计算方法：小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商0，点上小数点。

如果有余数，要添0再除。

2、除数是小数的除法的计算方法：先将除数和被除数扩大相同的倍数（把小数点向右移动相同的位数），使除数变成整数，再按“除数是整数的小数除法”的法则进行计算。

注意：向右移动小数点时，如果被除数的位数不够，在被除数的末尾用0补足。

3、除法中的变化规律：①商不变性质：被除数和除数同时乘或除以同一个数（0除外），商不变。

②除数不变，被除数乘或除以几，商随着乘或除以几。

③被除数不变，除数乘或除以几，商就除以或乘几。

④被除数大于除数，商就大于1；被除数小于除数，商就小于1。

⑤一个非0的数除以大于1的数，商就小于被除数；一个非0的数除以小于1的数，商就大于被除数。

⑥积不变性质：一个因数乘一个数，另一个除以同一个数（0除外），积不变。

⑦一个因数不变，另一个数乘几，积就乘几。

⑧一个因数不变，另一个因数除以几，积就除以几。

4、求商时有时也需要求近似数。

方法三种。

取商的近似数时，保留到哪一位，一定要除到那一位的下一位，然后用四舍五入的方法取近似数。

没有要求时，除不尽的一般保留两位小数。

5、一个数的小数部分，从某一位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

一个循环小数的小数部分，依次不断重复出现的数字，叫循环节。

如6.3232……的循环节是32，注意不是23一定要是第一次重复出现的数字是3在前2在后重复出现！6、循环小数的记法：（1）用省略号表示。

写出两个完整的循环节，加省略号。

如：3.55…， 2.0321321…（2）简便记法。

在循环节的首位和末位上加小圆点。

如0.36，2.587循环小数是无限小数，无限小数不一定是循环小数。

7、小数部分的位数是有限的小数，叫做有限小数。

第三章 插值法与最小二乘法1. 已知下列表值x 10 11 12 13 lnx 2.3026 2.3979 2.4849 2.5649用线形插值与二次Lagrange 插值计算ln11.75的近似值，并估计误差。

解：（1）线形插值说明：当插值点落在被插区间之内，这种方法称为内插法，此时插值精度较好。

x ],12,11[75.11∈=故选择x 0=11,x 1=12,求线形插值函数。

11001y x l y x l x P ⨯+⨯=∴）（）（）（=10100101y x x x x y x x x x ⨯--+⨯--=4849.21112113979.2121112⨯--+⨯--x x=2.4849（x-11）-2.3979（x-12）)1275.11(3979.2)1175.11(4849.2)75.11(75.11ln 1---=≈∴p =2.46315（2）二次拉格朗日插值选择插值结点：x 12,11,10210===x x P 2211002)()()()(y x l y x l y x l x ++= =212021012101200201021))(())(())(())(())(())((y x x x x x x x x y x x x x x x x x y x x x x x x x x ----+----+----=4849.2)1112)(1012()11)(10(3979.2)1211)(1011()12)(10(3026.2)1210)(1110()12)(11(----+----+----x x x x x x=1.1513（x-11）（x-12）-2.3979（x-10）（x-12）+1.24425（x-10）（x-11）)1175.11)(1011075(24245.1)1275.11)(1075.11(3979.2)1275.11)(1175.11(1513.1)75.11(75.11ln 2--+-----=≈∴P =1.15133125.124245.14375.03979.2)1875.0(⨯+⨯+-⨯ =2.4639282. 已知下列表值求f(x)在[0，2]之间零点近似值。

概率计算方法总结在新课标实施以来，中考数学试题中加大了统计与概率部分的考查，体现了“学以致用”这一理念. 计算简单事件发生的概率是重点，现对概率计算方法阐述如下: 一.公式法 P(随机事件)=的结果数随机事件所有可能出现果数随机事件可能出现的结.其中P(必然事件)=1,P （不可能事件）=0；0<P(随机事件)<1.例1 (河北)图1中每一个标有数字的方块均是可以翻动的木牌，其中只有两块木牌的背面贴有中奖标志，则随机翻动一块木牌中奖的概率为________．解析: 本题考查用公式法求概率,在随机翻动木牌过程中，一共有6种可能的翻牌结果,其中有2种为中奖,所以P(中奖)=3162 .说明: 本题采用了一种较为有趣的试题背景，重在考查学生对概率模型的理解、以及对随机事件发生概率值的计算. 二.面积法例2 如图2是地板格的一部分，一只蟋蟀在该地板格上跳来跳去，如果它随意停留在某一个地方，则它停留在阴影部分的概率是_______.解析：因为四块地板的面积各不相同，故应分别求出阴影部分的面积为2×1+2×3=8，总面积为：2×1+2×2+2×3+1×5=17，面积之比即为所求概率. 所以P(随意停留在阴影部分)=178. 评注:几何概型也就是概率的大小与面积大小有关,事件发生的概率等于此事件所有可能结果所组成的图形面积除以所有可能结果组成的图形的面积. 三.树形图法例3 不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为12 . （1）试求袋中蓝球的个数.图1图2（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图法，求两次摸到都是白球的概率.解析：⑴设蓝球个数为x个.由题意得21122=++x∴x=1答：蓝球有1个（2）树状图如下：∴两次摸到都是白球的概率=61122=.说明:解有关的概率问题首先弄清：①需要关注的是发生哪个或哪些结果.②无论哪种都是机会均等的. 本题是考查用树状图来求概率的方法,这种方法比较直观,把所有可能的结果都一一罗列出来,便于计算结果.四.列表法例4 (山西)如图3，有四张编号为1，2，3，4的卡片，卡片的背面完全相同．现将它们搅匀并正面朝下放置在桌面上．（1）从中随机抽取一张，抽到的卡片是眼睛的概率是多少？（2）从四张卡片中随机抽取一张贴在如图4所示的大头娃娃的左眼处，然后再随机抽取一张贴在大头娃娃的右眼处，用树状图或列表法求贴法正确的概率．1 2 3图4图3黄白2白1蓝黄白1蓝黄白2解析:(1)所求概率是.2142= (2)解法一(树形图):共有12种可能的结果(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3).其中只有两种结果(1,2)和(2,1)是符合条件的,所以贴法正确的概率是.61122= 解法二(列表法):共有12种可能的结果(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3).其中只有两种结果(1,2)和(2,1)是符合条件的,所以贴法正确的概率是.61122= 评注:本题考查学生对用树状图或列表法求概率的掌握情况,用树状图法或列表法列举出的结果一目了然,当事件要经过多次步骤（三步以上)完成时,用这两种方法求事件的概率很有效.第一次抽取13 4 第二次抽取 23 4 32 4 42 3。

第3章 剪切和挤压的实用计算3.1 剪切的概念在工程实际中，经常遇到剪切问题。

剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-1a)，构件的变形主要表现为沿着与外力作用线平行的剪切面(n m -面)发生相对错动(图3-1b)。

图3-1工程中的一些联接件，如键、销钉、螺栓及铆钉等，都是主要承受剪切作用的构件。

构件剪切面上的内力可用截面法求得。

将构件沿剪切面n m -假想地截开，保留一部分考虑其平衡。

例如，由左部分的平衡，可知剪切面上必有与外力平行且与横截面相切的内力Q F (图3-1c)的作用。

Q F 称为剪力，根据平衡方程∑=0Y ，可求得F F Q =。

剪切破坏时，构件将沿剪切面(如图3-la 所示的n m -面)被剪断。

只有一个剪切面的情况，称为单剪切。

图3-1a 所示情况即为单剪切。

受剪构件除了承受剪切外，往往同时伴随着挤压、弯曲和拉伸等作用。

在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力，而只是给出了主要的受力和内力。

实际受力和变形比较复杂，因而对这类构件的工作应力进行理论上的精确分析是困难的。

工程中对这类构件的强度计算，一般采用在试验和经验基础上建立起来的比较简便的计算方法，称为剪切的实用计算或工程计算。

3.2 剪切和挤压的强度计算3.2.1 剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。

图3-2a 为一种剪切试验装置的简图，试件的受力情况如图3-2b 所示，这是模拟某种销钉联接的工作情形。

当载荷F 增大至破坏载荷b F 时，试件在剪切面m m -及n n -处被剪断。

这种具有两个剪切面的情况，称为双剪切。

由图3-2c 可求得剪切面上的剪力为2F F Q =图3-2由于受剪构件的变形及受力比较复杂，剪切面上的应力分布规律很难用理论方法确定，因而工程上一般采用实用计算方法来计算受剪构件的应力。

在这种计算方法中，假设应力在剪切面内是均匀分布的。