状态和状态空间模型
- 格式:ppt
- 大小:669.50 KB
- 文档页数:46

自动控制原理状态空间知识点总结自动控制原理是研究控制系统的基本原理、分析方法和综合设计理论的一门学科。
状态空间方法是自动控制原理中的重要内容之一,它是一种模型描述和分析控制系统动态特性的数学工具。
在本文中,将对自动控制原理状态空间的知识点进行总结和概述。
一、状态空间模型的基本概念在自动控制系统中,状态是指系统在某一时刻的内部信息或特性。
状态空间模型是一种用状态来描述系统动态特性的数学模型。
它由状态方程和输出方程组成。
其中,状态方程描述了系统状态随时间的演化规律,而输出方程则说明了系统状态与外部输入之间的关系。
二、状态空间模型的表示方法状态空间模型可以用矩阵表示,常用的表示方法有传递函数表示法和状态方程表示法。
传递函数表示法是通过系统的输入和输出之间的关系来描述系统的动态特性,而状态方程表示法则是通过系统的状态方程来描述系统的动态特性。
三、状态空间模型的性质1. 可观测性:指系统的状态是否能够通过系统的输出来唯一确定,即是否存在唯一解。
2. 可控性:指系统的状态是否能够通过控制输入来控制,即是否存在能够使系统达到任意状态的控制输入。
3. 稳定性:指系统在受到一定干扰或扰动后,是否能够以某种方式恢复到稳定状态。
四、状态空间模型的分析与设计方法状态空间模型的分析与设计方法包括系统的稳定性分析、传递函数与状态空间模型之间的转换、状态空间模型的求解方法等。
1. 稳定性分析:通过对状态空间模型的特征值进行分析,可以得到系统的稳定性信息。
2. 传递函数与状态空间模型之间的转换:传递函数和状态空间模型是描述系统动态特性的两种不同数学表达方式,它们之间可以相互转换。
3. 状态空间模型的求解方法:通过对状态空间模型的求解可以得到系统的时域响应和频域响应等信息。
五、状态观测器与状态反馈控制器状态观测器是一种用于估计系统状态的装置,通过对系统的输出进行测量,并结合系统的数学模型,可以对系统的状态进行估计。
状态反馈控制器是一种利用系统的状态信息对系统进行控制的装置,通过对系统状态进行测量,并将测量值带入控制器中进行计算,从而实现对系统的控制。


状态空间模型状态空间模型是一种用于描述动态系统行为的数学模型。
在状态空间模型中,系统的行为由状态方程和观测方程确定。
状态方程描述系统状态如何随时间演变,而观测方程则描述系统状态如何被观测。
通过利用状态空间模型,我们可以对系统进行建模、预测和控制。
状态空间模型的基本概念状态空间模型通常由以下几个要素构成:1.状态变量(State Variables):描述系统状态的变量,通常用向量表示。
状态变量是系统内部的表示,不可直接观测。
2.观测变量(Observation Variables):直接观测到的系统状态的变量,通常用向量表示。
3.状态方程(State Equation):描述状态变量如何随时间演变的数学方程。
通常表示为状态向量的一阶微分方程。
4.观测方程(Observation Equation):描述观测变量与状态变量之间的关系的数学方程。
状态空间模型的应用状态空间模型在许多领域都有着广泛的应用,包括控制系统、信号处理、经济学和生态学等。
其中,最常见的应用之一是在控制系统中使用状态空间模型进行系统建模和控制设计。
在控制系统中,状态空间模型可以用于描述系统的动态行为,并设计控制器来实现系统性能的优化。
通过对状态方程和观测方程进行数学分析,可以确定系统的稳定性、可控性和可观测性,并设计出满足特定要求的控制器。
状态空间模型的特点状态空间模型具有以下几个特点:1.灵活性:可以灵活地描述各种复杂系统的动态行为,适用于各种不同的应用领域。
2.结构化:将系统分解为状态方程和观测方程的结构使得系统的分析更加清晰和系统化。
3.预测性:通过状态空间模型,可以进行系统状态的预测和仿真,帮助决策者做出正确的决策。
4.优化性:可以通过状态空间模型设计出有效的控制器,优化系统的性能指标。
在实际应用中,状态空间模型可以通过参数估计和参数辨识等方法进行模型的训练和调整,以适应实际系统的特性。
结语状态空间模型是一种强大的数学工具,可以帮助我们理解和分析动态系统的行为。

现代控制工程-第2章状态空间数学模型ModernControlEngineering教材:王万良,现代控制工程,高等教育出版社,2022状态空间方法是基于状态空间模型分析与设计自动控制系统。
状态空间模型描述了系统内部状态和系统输入、输出之间的关系,比输入输出模型更深入地揭示了系统的动态特性。
本章首先介绍状态的概念以及状态空间模型的建立方法,然后介绍系统的状态空间模型的实现,为系统分析与设计奠定基础。
22.1状态与状态空间的概念2.2系统的状态空间模型2.3线性系统的状态空间模型与线性变换2.4控制系统的实现2.5多变量系统的传递矩阵2.6控制系统的离散状态空间模型32.1状态与状态空间的概念例:图2.1所示弹簧-阻尼器系统在外作用力F(t)已知的情况下,如果知道了物体在某一时刻的位移及速度,就能确定系统未来的动态响应。
如果仅知道物体的位移或速度,就不能确定系统未来的动态响应。
物体的位移、速度及加速度这三个量显然是不独立的,可以根据其中两个量确定另外一个量,因此这个量对于描述系统状态是多余的。
可选择物体在某一时刻的位移及速度为弹簧-阻尼器系统在某一时刻的状42.1状态与状态空间的概念状态是系统中一些信息的集合,在已知未来外部输入的情况下,这些信息对于确定系统未来的行为是充分且必要的。
系统在各个时刻的状态是变化的,能够确定系统各个时刻状态的具有最少个数变量的一组变量称为状态变量。
以n个状态变量作为坐标轴所组成的维空间称为状态空间。
状态轨迹:以某(t)某(t0)为起点,随着时间的推移,某(t)在状态空间绘出的一条轨迹。
52.2系统的状态空间模型2.2.1建立状态空间模型的方法描述系统状态变量和输入变量之间关系的一阶微分方程组称为状态方程。
描述系统输出变量与系统状态变量、输入变量之间关系的方程称为输出方程。
系统的状态方程和输出方程组成系统的状态空间模型,或称为动态方程。
状态空间模型描述了系统内部状态和系统输入、输出之间的关系,所以又称为内部描述模型。



状态空间模型的实现及状态方程的解实验总结以状态空间模型的实现及状态方程的解实验总结为标题状态空间模型是一种描述动态系统行为的数学模型,通过将系统的状态、输入和输出量化为向量形式,以状态方程和输出方程的形式表示系统的动态行为。
在实际应用中,状态空间模型常用于控制系统的设计和分析。
在状态空间模型中,系统的状态由一组变量表示,这些变量描述了系统在不同时间点的状态。
状态方程描述了状态随时间的演化规律,是系统动态行为的核心部分。
状态方程通常采用微分方程的形式表示,其中包含系统的状态变量、输入和系统参数。
解状态方程可以得到系统状态随时间的变化情况,从而可以对系统的动态行为进行分析和预测。
在实验中,我们可以通过实际测量或仿真来获取系统的输入和输出数据,并根据这些数据来估计系统的状态方程和参数。
然后,利用已知的状态方程和输入数据,可以通过数值求解方法来解状态方程,得到系统的状态随时间的变化情况。
解状态方程的结果可以与实际测量或仿真数据进行比较,以验证状态方程的准确性和模型的有效性。
在进行状态空间模型实验时,需要注意以下几点:1. 系统建模:首先需要对系统进行建模,确定系统的状态变量、输入和输出,并推导出系统的状态方程和输出方程。
建模的过程中需要考虑系统的特性和约束条件,以及系统的稳定性和可控性等因素。
2. 实验设计:根据系统的特点和实验目的,设计合适的实验方案。
选择合适的输入信号,以及采样频率和采样时长等参数,以确保实验数据的准确性和可靠性。
3. 数据采集:在实验中需要采集系统的输入和输出数据。
输入信号可以通过外部激励或系统自身的反馈信号来产生,输出信号可以通过传感器或测量设备进行采集。
采集到的数据需要进行预处理和滤波,以去除噪声和干扰,提高数据的质量和可靠性。
4. 系统辨识:通过实验数据和已知的输入信号,利用数值辨识方法来估计系统的状态方程和参数。
常用的辨识方法包括最小二乘法、卡尔曼滤波器和系统辨识工具箱等。

引言状态空间模型是应用状态空间分析法对动态系统所建立的一种数学模型,它是应用现代控制理论对系统进展分析和综合的根底。
状态空间模型由描述系统的动态特性行为的状态方程和描述系统输出变量与状态变量间变换关系的输出方程组成。
在经典控制理论中,采用n阶微分方程作为对控制系统输入量u〔t〕和输出量y〔t〕之间的时域描述,或者在零初始条件下,对n阶微分方程进展Laplace 变换,得到传递函数作为对控制系统的频域描述,“传递函数〞建立了系统输入量U(s)=L[u(t)]和输出量Y(s)=L[y(t)]之间的关系。
传递函数只能描述系统的外部特性,不能完全反映系统内部的动态特征,并且由于只考虑零初始条件,难以反映系统非零初始条件对系统的影响。
现代控制理论是建立在“状态空间〞根底上的控制系统分析和设计理论,它用“状态变量〞来刻画系统的内部特征,用“一阶微分方程组〞来描述系统的动态特性。
系统的状态空间模型描述了系统输入、输出与内部状态之间的关系,提醒了系统内部状态的运动规律,反映了控制系统动态特性的全部信息。
龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
由于此算法精度高,采取措施对误差进展抑制,所以其实现原理也较复杂。
该算法是构建在数学支持的根底之上的。
标准四阶龙格——库塔法的根本思想龙格和库塔提出了一种间接地运用Taylor公式的方法,即利用y(x)在假设干个待定点上的函数值和导数值做出线性组合式,选取适当系数使这个组合式进Taylor展开后与y(xi+1)的Taylor展开式有较多的项到达一致,从而得出较高阶的数值公式,这就是龙格—库塔法的根本思想。
一、实验原理龙格——库塔法龙格—库塔法是仿真中应用最广泛的方法。
它以泰勒展开公式为根底,用函数f的线性组合代替f的高阶导数项,防止了高阶导数的运算,又提高了精度。
泰勒公式的阶次取得越高,龙格—库塔法所得的误差等级越低,精度越高。
最常用的是四阶龙格—库塔法,它虽然有一定的时间损耗,但比梯形法要快,而且与其它方法比拟,其误差比欧拉法高三个数量级,比预估—校正法高两个数量级,是自启动的。

状态空间模型表达式以状态空间模型为标题的文章状态空间模型是一种用于描述系统行为的数学模型。
它将系统的行为抽象为一系列状态和状态之间的转换关系。
在这个模型中,系统的行为可以被分解为一系列离散的状态,每个状态都代表着系统在某个时刻的特定情况。
通过定义状态之间的转换规则,我们可以描述系统在不同状态下的行为。
在状态空间模型中,系统的状态可以用变量来表示。
每个状态变量都有一组可能的取值,这些取值被称为状态空间。
系统的初始状态被称为初始状态,而系统的所有可能状态的集合被称为状态空间。
状态空间模型可以被用于描述各种不同的系统,包括物理系统、生物系统、信息系统等。
状态空间模型的核心是状态转换规则。
状态转换规则定义了系统在不同状态下的行为。
它描述了系统从一个状态转换到另一个状态的条件和方式。
状态转换规则可以用逻辑表达式、状态转移图等形式来表示。
通过定义状态转换规则,我们可以预测系统在不同状态下的行为,以及系统从一个状态转换到另一个状态的路径。
状态空间模型可以用于解决各种实际问题。
例如,在控制系统中,我们可以使用状态空间模型来描述系统的动态行为,设计控制器来实现系统的稳定性和性能要求。
在计算机科学中,我们可以使用状态空间模型来描述算法的执行过程,分析算法的时间复杂度和空间复杂度。
在人工智能领域,我们可以使用状态空间模型来描述智能代理的知识和行为,实现自动决策和自主学习。
状态空间模型的优点是可以提供对系统行为的精确描述。
通过定义状态和状态转换规则,我们可以准确地描述系统在不同状态下的行为,从而可以预测系统的行为和优化系统的性能。
此外,状态空间模型还可以提供对系统的可达性和可控性的分析,以及对系统的稳定性和鲁棒性的评估。
然而,状态空间模型也存在一些限制和挑战。
首先,状态空间模型假设系统的行为是离散的,而实际系统的行为往往是连续的。
因此,在描述连续系统时,需要对状态空间模型进行离散化处理。
其次,状态空间模型的规模随着系统状态的增加而指数级增长,这会导致模型的复杂性和计算复杂性的增加。

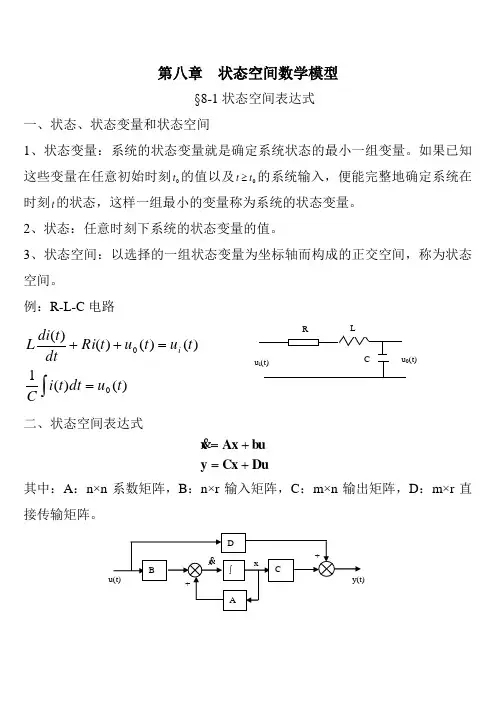
第八章 状态空间数学模型§8-1状态空间表达式一、状态、状态变量和状态空间1、状态变量:系统的状态变量就是确定系统状态的最小一组变量。
如果已知这些变量在任意初始时刻0t 的值以及0t t ≥的系统输入,便能完整地确定系统在时刻t 的状态,这样一组最小的变量称为系统的状态变量。
2、状态:任意时刻下系统的状态变量的值。
3、状态空间:以选择的一组状态变量为坐标轴而构成的正交空间,称为状态空间。
例:R-L-C 电路)()(1)()()()(00t u dt t i Ct u t u t Ri dt t di L i ==++⎰二、状态空间表达式Du Cx y bu Ax x+=+=其中:A :n×n 系数矩阵,B :n×r 输入矩阵,C :m×n 输出矩阵,D :m×r 直接传输矩阵。
例1:R-L-C 电路[]⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+--=0000001001011111u i u u L u i CL L Rdt du dt di i cdt du u L u L i L R dt di ii例:直流电动机[]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎩⎪⎨⎧--=+--===++==++ωωωωωωωωωωi T u J L i J c Jk L k L R dt d dt di T J J c i J k dtd u L L k i L R dt diik T T T c dt d J k e u e Ri dt di L l i te lt i e t l e i10100111§8-2由微分方程求状态空间表达式一、输入不含有导数项[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---========+++32132121032110213233221101200100100010x x x y u b x x x a a a x x x bu x a x a x a y x y x x y x xyx bu y a y a ya y二、输入含有导数项)()()()(:,:10213242211000312011202213001230011223011220210102132432104210310201333210422210311102010123012=+++---=--=-==+++=+++++++++++++++++=+++=++=+=-=----=-=---=-=--=-=+++=+++x a x a x a x a a a b a a b a b b u b u b u b u b u a a a ua a u a ux a x a x a x u u u ux y u u u x yu u x y u x y u x u u u u y x u x u u u yx u x u u yx uy x u b u b u b u b y a y a y a y βββββββββββββββββββββββββββββββββββββββββββ对应项系数相等整理得代入原方程得到[]u x x x u x y u x x x a a a x x x u x a x a x a xu x xu x x0321013213212132133221103232121001100010ββββββββ+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=+=+=§8-3传递函数矩阵一、传递函数矩阵Du Cx y Bu Ax x+=+=BA sI s G x x s Bu s x A sI s Bu s Ax x s sx xu 1][)(0)0()0()()(][)()()0()(--==+=-+=-Guy =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=+-=+-=+=--mrm m r r yuyu g g g g g g g g g G DB A sIC G s Du s Bu A sI C s Du s Cx s y21222211121111][)()(][)()()( 二、闭环系统传递函数矩阵)()]()([)()()()]()([)]()()()[()]()()[()()()()()()()()()()(1s G s H s G I G s u s G s y s H s G I s y s H s u s G s B s u s G s y s E s G s H s y s H s B s B s u s E close -+==+-=-===-=§8-4线性变换一、等价系统方程(状态变量的非唯一性)DD CP C u D x C Du x CP y PB B PAPA uB x A PBu x PAP PBu PAx Bu Ax P x P x x P x Pxx n n P Du Cx y Bu Ax x==+=+===+=+=+=+====⨯+=+=-----11111)(: 非奇异矩阵[]01101100101100110,11100222112110000====⎥⎥⎦⎤⎢⎢⎣⎡==⎥⎥⎦⎤⎢⎢⎣⎡--==⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-----D D CP C LC PB B L R LCPAP A C PCP u i Cu i P P P P u u u u C L R 为状态变量和若选电路为例以二、化系数矩阵为标准形的特征向量。