7机械的运转及其速度波动的调节答案

第七章 机械的运转及其速度波动的调节1一般机械的运转过程分为哪三个阶段?在这三个阶段中,输入功、总耗功、动能及速度之间的关系各有什么特点？2为什么要建立机器等效动力学模型？建立时应遵循的原则是什么？3在机械系统的真实运动规律尚属未知的情况下，能否求出其等效力矩和等效转动惯量？为什么？4飞轮的调速原理是什么？为什么说飞轮在调速的同时还能起到节约能源的作用？ 5何谓机械运转的"平均速度"和"不均匀系数"？6飞轮设计的基本原则是什么？为什么飞轮应尽量装在机械系统的高速轴上？系统上装上飞轮后是否可以得到绝对的匀速运动？7机械系统在加飞轮前后的运动特性和动力特性有何异同（比较主轴的ωm ，ωmax ，选用的原动机功率、启动时间、停车时间，系统中主轴的运动循环周期、系统的总动能）？ 8何谓最大盈亏功？如何确定其值？9如何确定机械系统一个运动周期最大角速度Wmax 与最小角速度Wmin 所在位置？ 10为什么机械会出现非周期性速度波动，如何进行调节？ 11机械的自调性及其条件是什么？ 12离心调速器的工作原理是什么？13对于周期性速度波动的机器安装飞轮后，原动机的功率可以比未安装飞轮时 。

14 若不考虑其他因素，单从减轻飞轮的重量上看，飞轮应安装在 轴上。

15大多数机器的原动件都存在运动速度的波动，其原因是驱动力所作的功与阻力所作的 功 保持相等。

16机器等效动力学模型中的等效质量（转动惯量）是根据系统总动能 的原则进行转化的，因而它的数值除了与各构件本身的质量（转动惯量）有关外，还与构件 的 有关。

17当机器中仅包含速比为 机构时，等效动力学模型中的等效质量（转动惯量）是常数；若机器中包含 自由度的机构时，等效质量（转动惯量）是机构位置的函数。

18 图示行星轮系中,各轮质心均在其中心轴线上，已知J 1001=.kg ⋅m 2,J 2004=.kg ⋅m 2，J 2001'.=kg ⋅m 2，系杆对转动轴线的转动惯量J H =018.kg ⋅m 2，行星轮质量m 2=2kg ，m 2'=4kg ，0.3H l =m ，13H i =-，121i =-。

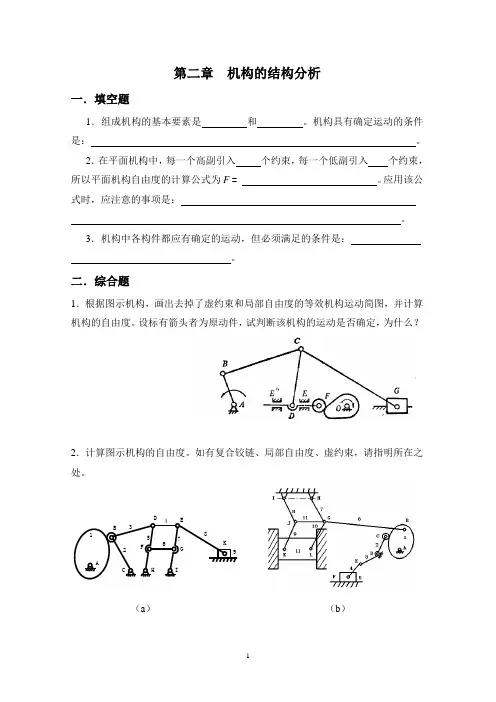
第二章 机构的结构分析一．填空题1．组成机构的基本要素是 和 。

机构具有确定运动的条件是： 。

2．在平面机构中，每一个高副引入 个约束，每一个低副引入 个约束，所以平面机构自由度的计算公式为F = 。

应用该公式时，应注意的事项是： 。

3．机构中各构件都应有确定的运动，但必须满足的条件是： 。

二．综合题1．根据图示机构，画出去掉了虚约束和局部自由度的等效机构运动简图，并计算机构的自由度。

设标有箭头者为原动件，试判断该机构的运动是否确定，为什么？2．计算图示机构的自由度。

如有复合铰链、局部自由度、虚约束，请指明所在之处。

（a ） （b ）ADECHGF IBK1234567893．计算图示各机构的自由度。

（a）（b）（c）（d）（e）（f）4．计算机构的自由度，并进行机构的结构分析，将其基本杆组拆分出来，指出各个基本杆组的级别以及机构的级别。

（a）（b）（c）（d）5．计算机构的自由度，并分析组成此机构的基本杆组。

如果在该机构中改选FG 为原动件，试问组成此机构的基本杆组是否发生变化。

6．试验算图示机构的运动是否确定。

如机构运动不确定请提出其具有确定运动的修改方案。

（a）（b）第三章平面机构的运动分析一、综合题1、试求图示各机构在图示位置时全部瞬心的位置（用符号P直接在图上标出）。

ij2、已知图示机构的输入角速度ω1,试用瞬心法求机构的输出速度ω3。

要求画出相应的瞬心，写出ω3的表达式，并标明方向。

3、在图示的齿轮--连杆组合机构中，试用瞬心法求齿轮1与3的传动比ω1/ω2。

4、在图示的四杆机构中，AB l =60mm, CD l =90mm, AD l =BC l =120mm, 2ω=10rad/s ，试用瞬心法求：（1）当ϕ=165°时，点C 的速度c v ；（2）当ϕ=165°时，构件3的BC 线上速度最小的一点E 的位置及其速度的大小； （3）当0c v =u u u v时，ϕ角之值（有两个解）。

简答题：1.分别写出机器在起动阶段、稳定运转阶段和停车阶段的功能关系的表达式，并说明原动件角速度的变化情况。

起动阶段：W d ＝W c ＋E ，机械的角速度ω由零渐增至ωm稳定运行阶段：周期变速稳定运转：W d ＝W c ，ωm ＝常数，而ω作周期性变化等速稳定运转：W d ≡W c ω＝ωm ＝常数，停车阶段：E ＝－W c ，ω由ωm 渐减为零。

2. 图示为某机器的等效驱动力矩()d M ϕ和等效阻力矩()r M ϕ的线图，其等效转动惯量为常数，该机器在主轴位置角ϕ等于 π/2 时，主轴角速度达到max ω,在主轴位置角ϕ等于 2π 时，主轴角速度达到min ω。

3.机器等效动力学模型中，等效质量的等效条件是什么？试写出求等效质量的一般表达式。

不知道机构的真实的运动，能否求得其等效质量？ 为 什 么？答：等效质量的等效条件是：等效构件与原机械系统动能相等，一般表达式为：m e ＝∑[m i (v Si /v )2＋J Si (ωi /v )2]。

不知道真实运动不能求得等效质量，因为计算表达式中需要机构的具体运动参数。

机 器 等 效 动 力 学 模 型 中， 等 效 力 的 等 效 条 件 是 什 么？ 试 写 出 求 等 效 力 的 一 般 表 达 式。

不 知 道 机 器 的 真 实 运 动， 能 否 求 出 等 效 力？ 为 什 么？ 答：等效力的等效条件是：等效构件与原机械系统的瞬时功率相等，一般表达式：F e ＝∑[F i cos αi (v i /v )± M i (ωi /v )]，不知道真实运动不能求得等效力，因为计算表达式中需要机构的具体运动参数。

填空题：1. 设某机器的等效转动惯量为常数，则该机器作匀速稳定运转的条件在每一瞬时,驱动功率等于阻抗功率 ， 作变速稳定运转的条件是 在一个运动周期中，驱动功等于阻抗功 。

2. 机器中安装飞轮的原因，一般是为了 调节周期性速度波动，同时还可获得降低原动机功率 的效果。

快释放。

（7）机器中安装飞轮后，可以。

A．使驱动功与阻力功保持平衡；B．增大机器的转速；C．调节周期性速度波动；D．调节非周期性速度波动。

（8）在周期性速度波动中，一个周期内机器的盈亏功之和是。

A．大于0 B．小于0 C．等于0（9）有三个机构系统，它们主轴的ωmax和ωmin分别是：A．1025rad/s，975rad/s；B．512.5rad/s，487.5md/s；C．525rad/s，475rad/s。

其中，运转最不均匀的是，运转最均匀的是。

（10）下列说法中，正确的是。

A．机械的运转速度不均匀系数的许用值[δ]选得越小越好，因为这样可以使机械的速度波动较小；B．在结构允许的条件下，飞轮一般装在高速轴上；C．在结构允许的条件下，飞轮一般装在低速轴上；D．装飞轮是为了增加机械的重量，从而使机械运转均匀。

（11）一机器的能量指示图如图所示，最大盈亏功为。

A．70J；B．50J；C．120J；D．60J。

7-3 判断题（1）等效力矩是加在等效构件上的真实力矩，它等于加在机械系统各构件上诸力矩合力矩。

( )（2）在稳定运转状态下机构的周期性速度波动也可用调速器调节。

( )（3）机械系统的等效力矩等于该系统中所有力矩的代数和。

( )（4）在周期性速度波动的机器中，飞轮一般是安装在高速轴上；假如把飞轮安装在低速轴上，也能起到调速作用。

( )7-4 如图所示为一机床工作台的传动系统，设已知各齿轮的齿数，齿轮3的分度圆半径r3，各齿轮的转动惯量J1、J2、J2′、J3，因为齿轮1直接装在电动机轴上，故J1中包含了电动机转子的转动惯量，工作台和被加工零件的重量之和为G。

当取齿轮1为等效构件时，试求该机械系统的等效转动惯量J e。

解：想一想：①何谓等效构件？何谓等效力和等效力矩？何谓等效质量与等效转动惯量？②为什么要建立机器等效力学模型？建立时应遵循的原则是什么？建立机器等效力学模型的意义何在？7-5 图示的导杆机构中，已知l AB=100mm，ϕ1=90°，ϕ3=30°；导杆3对轴C的转动惯量J C=0.016 kg·m2，其他构件的质量和转动惯量均忽略不计；作用在导杆3上的阻力矩M3=10N·m。

第六章 机械的运转及其速度波动的调节一、思考题答案1．答：在机器的运转过程中，由于作用在机构上的驱动力矩和阻抗力矩作周期性的变化，故使机器主轴的速度发生周期性的波动，这种速度波动叫周期性速度波动。

若等效力矩的变化是非周期性的，则机械运转的速度将出现非周期性的速度波动。

如果对速度波动不加以调节，将导致运动副中产生附加的动压力，引起机械的振动，从而降低机械的寿命、机械效率和工作质量。

周期性速度波动可以用加飞轮的办法加以调节；非周期性的速度波动一般用调速器来调节。

2．答：机器运转的“平均转速”是指在一个周期内等效构件转动速度的平均值。

在实际工程中，常近似的用其算术平均值来计算。

运转速度“不均匀系数”是指速度波动的幅度与平均值之比，即mωωωδminmax −=。

许用的[δ]不是越小越好，要根据不同类型的机械提出不同的要求。

3．答：机器安装了飞轮以后能减小速度波动的程度，但不能得到绝对匀速运转。

飞轮不能用来调节非周期性速度波动。

欲减小机器的周期性速度波动,转动惯量相同的飞轮应安装在机器的高速轴上。

4．答：飞轮设计的基本问题是确定飞轮的转动惯量。

最大盈亏功即为驱动功与阻抗功之差的最大值，一般为等效力矩图中盈功或亏功的最大值。

二、练习题答案6-1 解：(1) 由一个周期内，驱动功＝阻抗功，得： max 1222d r M M ππ= 即： max 11002d r M M N ==M （2） 画出能量指示图由能量指示图可看出，等效构件的最大ωmax 出现在2π，最小角速度ωmin 出现在32π。

π/23π/2200NM－图6-1(3) 由能量指示图可看出，最大盈亏功max 110050()2W J ππΔ==(4) 若运转速度不均匀系数[]0.125δ=，则应在等效构件上加的飞轮转动惯量为max 222250500.140.14[]200.125200.1250.143()F c m W J J kgm ππωδπΔ=−=−=−××=−=6-2解：由一个周期内，驱动功＝阻抗功，得：2800400800224d M ππππ=++即： 400d M NM =画出能量指示图图6-2＋＋π/23π/2－—+由能量指示图可看出，等效构件的最大ωmax 出现在，最小角速度0ωmin 出现在54π。

第七章 机械的运转及其速度波动的调节一．学习指导与提示在做机械的运动分析和受力分析时，都认为原动件的运动规律是已知的并且做等速运动。

实际上，原动件的真实运动规律与作用在机械上的外力、原动件的位置和所有构件的质量、转动惯量等因素有关，因而在一般条件下，原动件的速度和加速度是随着时间而变化的。

因此设计机械时，如果对执行构件的运动规律有比较严格的要求，或者需要精确地进行力的计算和强度计算时，就需要首先确定机械在外力作用下的真实运动规律。

1、以角速度ω作定轴转动的等效构件的等效参量的计算如等效构件以角速度ω作定轴转动，其动能为：E J e =122ω组成机械系统的各构件或作定轴转动，或作往复直线移动，或作平面运动，各类不同运动形式的构件动能分别为：E J i si i =122ωE m v i i si =122 E J i si i =122ω+122m v i si整个机械系统的动能为：E J i n si i ==∑1212ω + i n i si m v =∑1212式中：ωi 为第i 个构件的角速度；m i 为第i 个构件的质量；J si 为第i 个构件对其质心轴的转动惯量；v si 为第i 个构件质心处的速度。

由于等效构件的动能与机械系统的动能相等，则有：122J e ω = i n si i J =∑1212ω+ i n i si m v =∑1212 方程两边统除以122ω，可求解等效转动惯量：J e = i n si i J =∑12（ωω) +21)(ωsi i n i v m ∑=2．周期性速度波动调节与非周期性速度波动调节机械在某段工作时间内，若驱动力所作的功大于阻力所作的功，则出现盈功；若驱动力所作的功小于阻力所作的功，则出现亏功。

盈功和亏功将引起机械动能的增加和减少，从而引起机械运转速度的波动。

机械速度波动会使运动副中产生附加的动压力，降低机械效率，产生振动，影响机械的质量和寿命。

第七章 机械的运转及其速度波动的调节1一般机械的运转过程分为哪三个阶段在这三个阶段中,输入功、总耗功、动能及速度之间的关系各有什么特点2为什么要建立机器等效动力学模型建立时应遵循的原则是什么3在机械系统的真实运动规律尚属未知的情况下，能否求出其等效力矩和等效转动惯量为什么4飞轮的调速原理是什么为什么说飞轮在调速的同时还能起到节约能源的作用 5何谓机械运转的"平均速度"和"不均匀系数"6飞轮设计的基本原则是什么为什么飞轮应尽量装在机械系统的高速轴上系统上装上飞轮后是否可以得到绝对的匀速运动7机械系统在加飞轮前后的运动特性和动力特性有何异同（比较主轴的ωm ，ωmax ，选用的原动机功率、启动时间、停车时间，系统中主轴的运动循环周期、系统的总动能） 8何谓最大盈亏功如何确定其值9如何确定机械系统一个运动周期最大角速度Wmax 与最小角速度Wmin 所在位置 10为什么机械会出现非周期性速度波动，如何进行调节 11机械的自调性及其条件是什么 12离心调速器的工作原理是什么13对于周期性速度波动的机器安装飞轮后，原动机的功率可以比未安装飞轮时 。

14 若不考虑其他因素，单从减轻飞轮的重量上看，飞轮应安装在 轴上。

15大多数机器的原动件都存在运动速度的波动，其原因是驱动力所作的功与阻力所作的 功 保持相等。

16机器等效动力学模型中的等效质量（转动惯量）是根据系统总动能 的原则进行转化的，因而它的数值除了与各构件本身的质量（转动惯量）有关外，还与构件 的 有关。

17当机器中仅包含速比为 机构时，等效动力学模型中的等效质量（转动惯量）是常数；若机器中包含 自由度的机构时，等效质量（转动惯量）是机构位置的函数。

18 图示行星轮系中,各轮质心均在其中心轴线上，已知J 1001=.kg ⋅m 2,J 2004=.kg ⋅m 2，J 2001'.=kg ⋅m 2，系杆对转动轴线的转动惯量J H =018.kg ⋅m 2，行星轮质量m 2=2kg ，m 2'=4kg ，0.3H l =m ，13H i =-，121i =-。

机械原理--- 1第2章机构的结构分析一、正误判断题：在括号内正确的画“√”,错误的画“×”1.在平面机构中一个高副引入二个约束;×2.任何具有确定运动的机构都是由机架加原动件再加自由度为零的杆组组成的; √3.运动链要成为机构,必须使运动链中原动件数目大于或等于自由度;×4.平面机构高副低代的条件是代替机构与原机构的自由度、瞬时速度和瞬时加速度必需完全相同;√5.当机构自由度F＞0,且等于原动件数时,该机构具有确定运动;√6.若两个构件之间组成了两个导路平行的移动副,在计算自由度时应算作两个移动副;×7.在平面机构中一个高副有两个自由度,引入一个约束;√8.在杆组并接时,可将同一杆组上的各个外接运动副连接在同一构件上;×9.任何机构都是由机架加原动件再加自由度为零的基本杆组组成;因此基本杆组是自由度为零的运动链;√10.平面低副具有2个自由度,1个约束;×二、填空题1.机器中每一个制造单元体称为零件 ;2.机器是在外力作用下运转的,当外力作功表现为盈功时,机器处在增速阶段,当外力作功表现为亏功时,机器处在减速阶段;3.局部自由度虽不影响机构的运动,却减小了高副元素的磨损 ,所以机构中常出现局部自由度;4.机器中每一个独立的运动单元体称为构件 ;5.两构件通过面接触而构成的运动副称为低副；通过点、线接触而构成的运动副称为高副;6.平面运动副的最大约束数为 2 ,最小约束数为 1 ;7.两构件之间以线接触所组成的平面运动副,称为高副,它产生 2 个约束;三、选择题1.机构中的构件是由一个或多个零件所组成,这些零件间 B 产生任何相对运动;A.可以B.不能C.变速转动或变速移动2.基本杆组的自由度应为 C ;A.－1B. +1C. 03.有两个平面机构的自由度都等于1, 现用一个带有两铰链的运动构件将它们串成一个平面机构,则其自由度等于 B ;A. 0B. 1C. 24.一种相同的机构 A 组成不同的机器;A.可以B.不能C.与构件尺寸有关5.平面运动副提供约束为 C ;A．1 B．2 C．1或26.计算机构自由度时,若计入虚约束,则机构自由度就会 C ;A．不变 B．增多 C．减少7.由4个构件组成的复合铰链,共有 B 个转动副;A．2 B．3 C．48.有两个平面机构的自由度都等1,现用一个带有两铰链的运动构件将它们串成一个平面机构,则其自由度等于 B ;A 0B 1C 2第3章平面机构的运动分析一、判断题正确打√,错误打×1．速度瞬心是指两个构件相对运动时相对速度为零的点; √2. 利用瞬心既可以对机构作速度分析,也可对其作加速度分析; ×二、选择题1. 平面六杆机构有共有 C 个瞬心;A．6 B．12 C．15三、填空题1. 当两构件以转动副相连接时,两构件的速度瞬心在转动副的中心处 ;2. 不通过运动副直接相连的两构件间的瞬心位置可借助三心定理来确定;第5章机械的效率和自锁一、填空题1．从效率的观点来看,机械的自锁条件时效率≤ 0;2．机械发生自锁时,机械已不能运动,这时它所能克服的生产阻抗力≤0;第7章机械的运转及其速度波动的调节一、正误判断题：在括号内正确的画“√”,错误的画“×”1.为了使机器稳定运转,机器中必须安装飞轮;×2.机器中安装飞轮后,可使机器运转时的速度波动完全消除;×3.机器稳定运转的含义是指原动件机器主轴作等速转动;×4.机器作稳定运转,必须在每一瞬时驱动功率等于阻抗功率;×5.为了减轻飞轮的重量,最好将飞轮安装在机械的高速轴上;√二、选择题1、在最大盈亏和机器运转速度不均匀系数不变前提下,将飞轮安装轴的转速提高一倍,则飞轮的转动惯量将等于原飞轮转动惯量的 C ;2 C.1/42、为了减轻飞轮的重量,飞轮最好安装在 C 上;A.等效构件上B.转速较低的轴上C.转速较高的轴上3、若不改变机器主轴的平均角速度,也不改变等效驱动力矩和等效阻抗力矩的变化规律,拟将机器运转速度不均匀系数从降到,则飞轮转动惯量将近似等于原飞轮转动惯量的 A ;.100 C104、有三个机械系统,它们主轴的最大角速度和最小角速度分别是：11025转/秒,975转/秒;2转/秒,转/秒;3525转/秒 475转/秒;其中运转最不均匀的是 C ;A.1B.2C.35、对于存在周期性速度波动的机器,安装飞轮主要是为了在 B 阶段进行速度调节;A．起动 B．稳定运转 C．停车6、为了减小机械运转中周期性速度波动的程度,应在机械中安装 B ;A．调速器 B．飞轮 C．变速装置三、填空题1. 机器的周期性性速度波动可以用飞轮来调节, 非周期性速度波动必须用调速器来调节;2.把具有等效转动惯量 ,其上作用有等效力矩的绕固定轴转动的等效构件,称为原机械系统的等效动力学模型3.在机器中安装飞轮能在一定程度上减小机器的周期性速度波动量;4.对于机器运转的周期性速度波动,一个周期内驱动力与阻力所做的功是相同的;第8章平面连杆机构及其设计一、正误判断题：在括号内正确的画“√”,错误的画“×”1.曲柄摇杆机构的极位夹角一定大于零;×2.具有急回特性的四杆机构只有曲柄摇杆机构、偏置曲柄滑块机构和摆动导杆机构;√3.四杆机构处于死点位置时,机构的传动角一定为零√4.对于双摇杆机构,最短构件与最长构件长度之和一定大于其余两构件长度之和;×5.双摇杆机构一定不存在整转副; ×6.平面四杆机构的压力角大小不仅与机构中主、从动件的选取有关,而且还随构尺寸及机构所处位置的不同而变化;√7.摆动导杆机构一定存在急回特性;√8.在四杆机构中,当最短杆长度与最长杆长度之和大于其余两杆长度之和时,且以最短杆的邻边为机架,该机构为曲柄摇杆机构;×9.对心曲柄滑块机构无急回运动; √10.一个铰链四杆机构若为双摇杆机构,则最短杆长度与最长杆长度之和一定大于其余两杆长度之和; ×11.平面四杆机构处于死点位置时,机构的传动角等于零;√12.对心曲柄滑块机构,当曲柄为主动件时机构无急回特性; √13.满足“最短杆长度+最长杆长度≤其余两杆长度之和”的铰链四杆机构一定有曲柄存在;×14.在铰链四杆机构中,当行程速比系数K＞1时,机构一定有急回特性; √二、填空题1.在曲柄滑块机构中,滑块的极限位置出现在曲柄与连杆共线位置;2.在曲柄摇杆机构中,若以摇杆为原动件,则曲柄与连杆共线位置是死点位置;3.在曲柄摇杆机构中,当摇杆为主动件,且曲柄与连杆两次共线时,则机构出现死点位置;4.当四杆机构的压力角α=90°时,传动角等于 0° ,该机构处于死点位置;5.铰链四杆机构ABCD中,已知：l AB=60mm,l BC=140mm,l CD=120mm,l AD=100mm;若以AB杆为机架得双曲柄机构；若以CD杆为机架得双摇杆机构；若以AD杆为机架得曲柄摇杆机构;6.铰链四杆机构的基本形式有曲柄摇杆机构、双曲柄机构和双摇杆机构;三、选择题1.当四杆机构处于死点位置时,机构的压力角 B ;A.为0°B.为90°C.与构件尺寸有关2.铰链四杆机构中若最短杆和最长杆长度之和大于其他两杆长度之和时,则机构中 B ;A.一定有曲柄存在B. 一定无曲柄存在C. 是否有曲柄存在还要看机架是哪一个构件3.曲柄摇杆机构 B 存在急回特性;A . 一定 B. 不一定 C. 一定不4.平面四杆机构所含移动副的个数最多为 B ;A. 一个B. 两个C. 基圆半径太小5.四杆机构的急回特性是针对主动件作 A 而言的;A.等速转动B. 等速移动C.变速转动或变速移动6.对于双摇杆机构,最短构件与最长构件长度之和 B 大于其它两构件长度之和;A . 一定 B. 不一定 C. 一定不7.如果铰链四杆运动链中有两个构件长度相等且均为最短,若另外两个构件长度也相等,则当两最短构件相邻时,有 B 整转副;A. 两个B.三个C. 四个8.平行四杆机构工作时,其传动角 A ;A . 是变化值 B. 始终保持90度 C.始终是0度9.一曲柄摇杆机构,若改为以曲柄为机架,则将演化为 A ;A．双曲柄机构 B．曲柄摇杆机构 C．双摇杆机构10.曲柄摇杆机构中,当曲柄为主动件时,最小传动角出现在 A 位置;A．曲柄与机架共线 B．摇杆与机架共线 C．曲柄与连杆共线11.设计连杆机构时,为了具有良好的传动条件,应使 A ;A.传动角大一些,压力角小一些B.传动角和压力角都小一些C.传动角和压力角都大一些12.平面连杆机构的行程速比系数K值的可能取值范围是 A ;A．1≤K≤3 B．1≤K≤2 C．0≤K≤113.铰链四杆机构中有两个构件长度相等且最短,其余构件长度不同,若取一个最短构件作机架,则得到 C 机构;A 曲柄摇杆B 双曲柄C 双摇杆14.对心曲柄滑块机构以曲柄为原动件时,其最大传动角为 A ;m axA 90°B 45°C 30°15.下面那种情况存在死点 C ;A 曲柄摇杆机构,曲柄主动B 曲柄滑块机构,曲柄主动C 导杆机构,导杆主动16.要将一个曲柄摇杆机构转化成双摇杆机构,可以用机架转换法将C ;A 原机构的曲柄作为机架B 原机构的连杆作为机架C 原机构的摇杆作为机架17.在铰链四杆机构中,当满足“最短杆长度+最长杆长度≤其余两杆长度之和”时,以 A 机架,该机构为双摇杆机构;A 最短杆的对边B 最短杆C 最短杆的邻边18.无急回特性的平面连杆机构中,行程速比系数 B ;A K1B K=1C K119.在下列机构中,不会出现死点的机构是 A 机构;A 导杆从动机构B 曲柄从动摇杆C 曲柄从动滑块机构第9章凸轮机构及其设计一、正误判断题：在括号内正确的画“√”,错误的画“×”1.直动平底从动件盘形凸轮机构工作中,其压力角始终不变;√2.当凸轮机构的压力角的最大值超过许用值时,就必然出现自锁现象;×3.滚子从动件盘形凸轮机构中,基圆半径和压力角应在凸轮的实际廓线上来度量;×4.在直动从动件盘形凸轮机构中进行合理的偏置,是为了同时减小推程压力角和回程压力角; ×5.凸轮机构中,滚子从动件使用最多,因为它是三种从动件中的最基本形式; ×6.在凸轮理论廓线一定的条件下,从动件上的滚子半径越大,则凸轮机构的压力角越小; ×7.凸轮机构中,当推杆在推程按二次多项式运动规律运动时,在推程的起始点、中点及终止点存在刚性冲击;×8.凸轮机构中,在其他条件不变的情况下,基圆越大,凸轮机构的传力性能越好;√9.凸轮机构的从动件采用等速运动规律时可避免刚性冲击; ×10.在滚子推杆盘形凸轮机构中,凸轮的基圆半径应在凸轮的理论廓线上来度量; √11.凸轮机构的基圆越大则传力性能越好; √12.从动件按等加速等减速运动规律运动,是指从动件在推程中按等加速运动,而在回程中则按等减速运动,且它们的绝对值相等;×13.滚子从动件盘形凸轮的实际轮廓曲线是理论轮廓曲线的等距曲线;因此其实际轮廓上各点的向径就等于理论轮廓上各点的向径减去滚子半径;×二、填空题1.在推杆常用的运动规律中, 一次多项式运动规律会产生刚性冲击;2.由速度有限值的突变引起的冲击称为刚性冲击;3.增大基圆半径,凸轮廓线曲率半径增大 ;4.在推杆常用的多项式运动规律中, 五次多项式运动规律既不会产生柔性冲击,也不会产生刚性冲击;5.由加速度有限值的突变引起的冲击称为柔性冲击;6.减小基圆半径,凸轮机构的压力角增大;7.在推杆常用的运动规律中, 一次多项式运动规律会产生刚性冲击;8.按凸轮形状的不同,凸轮机构可分为盘形凸轮、移动凸轮和圆柱凸轮;三、选择题1.直动平底从动件盘形凸轮机构的压力角 B ;A.永远等于0度B.等于常数C.随凸轮转角而变化2.设计一直动从动件盘形凸轮,当凸轮转速及从动件运动规律V=VS不变时,若最大压力角由40度减小到20度时,则凸轮尺寸会 A ;A.增大B.减小C.不变3.对于转速较高的凸轮机构,为了减小冲击和振动,从动件运动规律最好采用C 运动规律;A.等速B.等加速等减速C.正弦加速度4.当凸轮基圆半径相同时,采用适当的偏置式从动件可以 A 凸轮机构推程的压力角A.减小B.增加C.保持原来5.凸轮机构中从动件作等加速等减速运动时将产生 B 冲击;A .刚性 B.柔性 C.无刚性也无柔性6.设计一直动从动件盘形凸轮,当凸轮转速及从动件运动规律V=VS不变时,若最大压力角由40度减小到20度时,则凸轮尺寸会 A ;A.增大B.减小C.不变7.若从动件的运动规律选择为等速运动规律、等加速等减速运动规律、简谐运动规律或正弦加速度运动规律,当把凸轮转速提高一倍时,从动件的速度是原来的 B 倍;A. 1B. 2C. 48.在设计滚子推杆盘形凸轮机构时,轮廓曲线出现尖顶是因为滚子半径 B该位置理论廓线的曲率半径;A．小于； B．等于 C．大于9.凸轮机构中推杆的运动规律决定于 A ;A．凸轮的轮廓形状 B．推杆的形状 C．凸轮的材料10.在设计滚子推杆盘形凸轮机构时,为防止凸轮的工作廓线出现变尖或失真现象,滚子半径应 B 凸轮的理论廓线外凸部分的最小曲率半径;A．大于； B．小于 C．等于11.在偏置直动尖顶推杆盘形凸轮机构中,基圆的大小会影响 A ;A．凸轮机构的压力角 B．推杆的位移 C．推杆的速度12.下列平面四杆机构中,一定无急回特性的机构是 A ;A 平行四边形机构B 曲柄摇杆机构C 偏置曲柄滑块机构13.尖顶从动件凸轮机构中,基圆的大小会影响 C ;A 从动件的位移B 凸轮的速度C 凸轮机构的压力角14.设计滚子从动件盘形凸轮轮廓曲线时,若将滚子半径加大,那么凸轮轮廓曲线上各点曲率半径 B ;A 变大B 变小C 不变15.当凸轮基圆半径相同时,采用适当的偏置式从动件可以 A 凸轮机构推程的压力角;A 减小B 增加C 保持原来16.在凸轮机构中,从动件的 A 运动规律存在刚性冲击;A 等速B 等加速等减速C 正弦加速度17.在凸轮机构中,若增大凸轮机构的推程压力角,则该凸轮机构的凸轮基圆半径将 B ;A 增大B 减小C 不变第10章齿轮机构及其设计一、正误判断题：在括号内正确的画“√”,错误的画“×”1.一对直齿圆柱齿轮啮合传动,模数越大,重合度也越大;×2.一对渐开线直齿圆柱齿轮的正确啮合条件是基圆齿距相等;√3.对于单个齿轮来说,节圆半径就等于分度圆半径;×4.根据渐开线性质,基圆之内没有渐开线,所以渐开线齿轮的齿根圆必须设计的比基圆大些;×5.一对外啮合的直齿圆柱标准齿轮,小轮的齿根厚度比大轮的齿根厚度大;×6.一对能正确啮合传动的渐开线直齿圆柱齿轮,其啮合角一定为20度;×7.渐开线直齿圆柱齿轮同一基圆的两同向渐开线为等距线; √8.一个渐开线圆柱外齿轮,当基圆大于齿根圆时,基圆以内部分的齿廓曲线,都不是渐开线;√9.一个渐开线圆柱外齿轮,当基圆大于齿根圆时,基圆以内部分的齿廓曲线仍是渐开线;×10.一对外啮合斜齿圆柱齿轮正确啮合的条件是两斜齿圆柱齿轮的端面模数和压力角分别相等,螺旋角大小相等,旋向相同;×11.因为基圆内没有渐开线,所以齿轮齿根圆必须大于基圆;×12.一对渐开线直齿圆柱齿轮刚好连续传动的重合度等于1;√13.渐开线直齿圆柱齿轮的分度圆与节圆相等;×14.斜齿圆柱齿轮在端面上的齿廓是标准渐开线齿廓;×15.当加工负变位齿轮时,刀具应向远离轮坯中心的方向移动;×二、填空题1.基圆的大小决定了渐开线的形状;2.齿轮变位不仅可以消除根切 ,而且可以改变齿轮传动的中心距 ;3.斜断轮传动的主要缺点是有轴向力,可采用人字齿轮来克服这一缺点;4.蜗杆传动用于交错两轴之间的运动和动力的传递;5.负变位直齿圆柱齿轮与标准直齿轮相比,其齿厚将会减小 ;6.圆锥齿轮用来传递相交两轴之间的运动和动力的传递;7.重合度大于1是齿轮的连续传动条件;8.渐开线标准直齿圆柱齿轮传动的正确啮合条件是两齿轮的模数和压力角分别相等 ;9.用范成法加工齿轮,当刀具齿顶线超过啮合极限点时,将会发生根切现象;10.渐开线直齿圆柱外齿轮齿廓上各点的压力角是不同的,它在基圆圆上的压力角为零,在分度圆上的压力角则取为标准值;11.蜗杆传动的中间平面是指通过蜗杆轴线并垂直于蜗轮轴线的平面;12.直齿圆柱齿轮机构的重合度愈大,表明同时参与啮合的轮齿对数愈多 ,传动愈平稳 ;13.正变位直齿圆柱齿轮与标准直齿圆柱齿轮相比,两者在分度圆上的压力角大小_相_等、模数m大小_ 相__等、分度圆大小不变;14.双头蜗杆每分钟240转,蜗轮齿数为80;则蜗轮每分钟 6 转;15.标准直齿圆柱齿轮的模数为2mm,齿数为20,则齿距等于 6.28 mm;16.渐开线齿廓在基圆上的曲率半径等于 0 ,渐开线齿条齿廓上任意一点的曲率半径等于 ;17.一对渐开线标准齿轮非标准安装时,节圆与分度圆不重合,分度圆的大小取决于模数和齿数 ;三、选择题1.渐开线直齿圆柱外齿轮顶圆压力角 A 分度圆压力角;A.大于B.小于C.等于2.一对渐开线直齿圆柱齿轮的啮合线切于 C ;A. 两分度圆B.两节圆C.两基圆3.一对渐开线标准齿轮在标准安装情况下,两齿轮分度圆的相对位置应该是 B ;A.相交的B.相切的C.分离的4.已知一渐开线标准直齿圆柱齿轮,齿数25,齿顶高系数为1,顶圆直径135mm, 则其模数大小应为 C ;A.2 mmB.4 mmC.5 mm5.为保证一对渐开线齿轮可靠地连续定传动比传动,应使实际啮合线长度A 基节;A.大于B.等于C.小于6.渐开线齿轮齿条啮合时,其齿条相对齿轮作远离圆心的平移时,其啮合角B ;A .加大 B.不变 C.减小7.一对渐开线直齿圆柱齿轮传动,其啮合角与节圆压力角C ;A ．可能相等可能不相等B ．一定不相等C ．一定相等8. 一对渐开线标准齿轮在标准安装情况下,两齿轮分度圆的相对位置应该是B ;A ．相交的B ．相切的C ．分离的9. 负变位齿轮分度圆上的齿距应是 C πm;A ．大于B ．小于C ．等于10.渐开线齿轮的齿廓离基圆越远,渐开线压力角就 A ;A 越大B 越小C 趋 近 于 2011.当一对渐开线齿轮切制成后,即使两轮的中心距稍有变化,其角速度比仍保持不变,原因是 B ;A 节圆半径不变B 基圆半径不变C 啮合角不变12.渐开线标准直齿圆柱外齿轮的齿数增加,齿顶圆压力角将 C ;A 不变B 增大C 减小13.满足正确啮合条件的一对直齿圆柱齿轮,其齿形 B 相同;A 一定B 不一定C 一定不14.标准蜗杆传动的中心距a 为 B ; A 2)(21z z m + B 2)(2z q m + C 221a a d d + 15.用齿条形刀具范成法加工标准齿轮时,齿轮产生根切的原因是 A ;A 齿轮齿数太少B 齿条刀齿数太少C 齿轮齿全高太长16.斜齿轮传动比直齿轮传动平稳,是因为 B ;A 斜齿轮有轴向力存在B 斜齿轮是逐渐进入和退出啮合的C 斜齿轮有法面模数17.变位齿轮在分度圆上的压力角 B 标准齿轮在分度圆上的压力角;A 小于B 等于C 大于第11章齿轮系及其设计一、正误判断题：在括号内正确的画“√”,错误的画“×”;1. 周转轮系中,自由度为2的轮系是行星轮系 ; ×二、填空题1.行星轮条中必须有一个中心轮是固定不动的;2.差动轮系的自由度为2;3.实现两轴间的多种速比传动,用定轴轮系是较方便的;三、选择题1．周转轮系中的差动轮系自由度为 C ;A．3 B．1 C．22．标准齿轮传动的实际中心距稍微大于标准中心距时,其传动比 B ;A．增大 B．不变 C．减小。

18图示行星轮系中，各轮质心均在其中心轴线上，已知m 2'=4kg ,用在轮1上的阻力矩 Mj^ON m 。

试求:（1） 等效到轮1上的等效转动惯量； （2） 等效到轮1上的等效力矩。

第七章机械的运转及其速度波动的调节1 一般机械的运转过程分为哪三个阶段 ？在这三个阶段中，输入功、总耗功、动能及速度之间 的关系各有什么特点？ 2为什么要建立机器等效动力学模型？建立时应遵循的原则是什么? 3在机械系统的真实运动规律尚属未知的情况下, 什么？ 能否求出其等效力矩和等效转动惯量？为 4飞轮的调速原理是什么？为什么说飞轮在调速的同时还能起到节约能源的作用？5何谓机械运转的"平均速度”和"不均匀系数” ？ 6飞轮设计的基本原则是什么？为什么飞轮应尽量装在机械系统的高速轴上？系统上装上 飞轮后是否可以得到绝对的匀速运动? （比较主轴的 伽,从ax ,选用的原 动机功率、启动时间、停车时间，系统中主轴的运动循环周期、系统的总动能）？ 7机械系统在加飞轮前后的运动特性和动力特性有何异同 8何谓最大盈亏功？如何确定其值? 9如何确定机械系统一个运动周期最大角速度 Wmax 与最小角速度Wmin 所在位置? 10为什么机械会出现非周期性速度波动，如何进行调节? 11机械的自调性及其条件是什么? 12离心调速器的工作原理是什么? 13对于周期性速度波动的机器安装飞轮后，原动机的功率可以比未安装飞轮时 14若不考虑其他因素，单从减轻飞轮的重量上看，飞轮应安装在 轴上。

15大多数机器的原动件都存在运动速度的波动，其原因是驱动力所作的功与阻力所作的功 _______________________________________ 保持相等。

16机器等效动力学模型中的等效质量（转动惯量）是根据系统总动能 _______ 则进行转化的，因而它的数值除了与各构件本身的质量（转动惯量）有关外，还与构件的原有关。

在图示的搬运机构中，已知滑块5 质量 5kg ，AB EDmm ， BCCD EFmm ，3 90 。

作用在滑块 5m=20l =l=100L =L =L =200123上的工作阻力5；其他构件的质量和转动惯量均忽略不计，如选构件1 为等效构件，试求机构在图示位置的等效阻F ＝1000N力矩 r 和等效转动惯量 e 。

MJ图【分析】对于本题，由于除滑块5 外，其余构件的质量和转动惯量均忽略不计。

所以只要求得v 5 / 1 的值，就可求得所需的等效阻力矩和等效转动惯量。

解： （1）求 v 5 / 1由于 123390 ，所以在矢量方程 v Cv Bv CB中，v C 和 v B 大小相等，方向相同； 同理，在矢量方程 v F v E v FE中，v F 和 v E 也是大小相等，方向相同。

对于构件CDEDv C / 2 。

这样：3，由于 L =2L ，所以 v Ev 5 v F 1 1 1 1lABv E v C v B2 2 2从而v 5lAB0.1 0.05m221(2) 求 M rvM r F 5 ( 5 ) 1000 0.05 50N m1(3) 求 J e根据公式 J en2 2 i 1 m i v SiJ Sii得：v 52J e m 520 0.05 2 0.05 kg m 21【评注】本例比较简单，关键在于进行运动分析，由于机构处于特殊位置，给速度的分析带来一定的困难，但只要弄清 楚速度的关系，特殊位置的机构速度分析又非常简单。

在图 (a) 所示的机构中，曲柄l 的长度为l 1，其对轴 A 的转动惯量为Jl。

连杆 2 的长度为l 2，质心在 S ，且l BS2/2，=l 质量为2，绕质心 S 的转动惯量为 J 2，滑块 3 为一齿条，质量为3。

齿轮 4 的转动惯量为J 4，其分度圆半径为r 4。

作用在机mm械上的驱动力矩为1，工作阻力矩为Q。

试求以曲柄 1 为等效构件时的等效转动惯量J e和等效力矩e 。

第七章 机械的运转及其速度波动的调节题7-7如图所示为一机床工作台的传动系统，设已知各齿轮的齿数，齿轮3的分度圆半径r 3，各齿轮的转动惯量J 1、J 2、J 2`、J 3，因为齿轮1直接装在电动机轴上，故J 1中包含了电动机转子的转动惯量，工作台和被加工零件的重量之和为G 。

当取齿轮1为等效构件时，试求该机械系统的等效转动惯量J e 。

解：根据等效转动惯量的等效原则，有∑=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ni i Si Si i e J v m J 122ωωω 2322123232213221222121⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+='''Z Z Z Z r g G Z Z Z Z J Z Z J Z Z J J J e 212133212221221⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=''ωωωωωωωv g G J J J J J e 题7-9已知某机械稳定运转时其主轴的角速度ωs =100rad/s ，机械的等效转动惯量J e =0.5Kg ·m 2，制动器的最大制动力矩M r =20N ·m （该制动器与机械主轴直接相联，并取主轴为等效构件）。

设要求制动时间不超过3s ，试检验该制动器是否能满足工作要求。

解：因此机械系统的等效转动惯量J e 及等效力矩M e 均为常数，故可利用力矩形式的机械运动方程式dtd J Me e ω= 其中：25.020m kg m N M M r e ⋅=⋅-=-= ωωωd d d M J dt r e 025.0205.0-=-=-= ()st S S 5.2025.0025.0==--=∴ωωω由于 s s t 35.2<= 所以该制动器满足工作要求。

题7-11 在图a 所示的刨床机构中，已知空程和工作行程中消耗于克服阻抗力的恒功率分别为P 1=367.7W 和P 2=3677W ，曲柄的平均转速n=100r/min ，空程中曲柄的转角φ1=120°。

第七章机械的运转及其速度波动的调节7.1本章知识点串讲本章的重点在于最大盈亏功﹑速度不均匀系数﹑等效转动惯量﹑等效质量﹑等效力矩﹑等效力的概念及计算方法，以及机械运转速度波动及其调节方法。

1．等效转动惯量﹑等效质量﹑等效力矩﹑等效力的计算方法等效转动惯量的一般计算式为：等效力矩的一般计算式为：等效质量的一般计算式为：等效力的一般计算式为:2．稳定运转条件下机械速度的波动及其调节一、周期性速度波动产生的原因作用在机械系统上的驱动力(矩)和(或)阻抗力(矩)和(或)系统等效转动惯量(质量)是机构位置的函数。

二、平均速度三、速度不均匀系数δ角速度(ωmax-ωmin)的变化幅度与其平均角速度ωm的比值。

四、周期性速度波动的调节原理赢功：驱动功大于阻抗功时，两者的差值；亏功：阻抗功大于驱动功时，两者的差值。

设：S1=300; S2=1500; S3=1300; S4=1700; S5=1600各点处的外力功值：a(0);b(-300);c(+1200);d(-100);e(1600);f(0)。

最小功值在b处，最大功值在e处；相对应最小速度在b处，最大速度在e处。

最大赢亏功ΔW max = ΔE max= Emax - Emin另外，最大赢亏功又等于ΔW max =Jeω2mδ由此得到调节方法：在ΔW max一定的情况下，为了使系统速度不均匀系数δ < [δ]，可通过给系统增加一个转动惯量较大的回转体——飞轮(其转动惯量计为Jf )。

五、飞轮转动惯量的计算飞轮转动惯量为Jf，于是有ΔW max = (Je + Jf )ω2mδ一般情况，Je <<Jf，故可忽略可忽略Je的影响。

于是：7.2本章重难点总结7.2.1重难点知识点总结本章的难点在于最大盈亏功﹑速度不均匀系数﹑等效转动惯量﹑等效质量﹑等效力矩﹑等效力等的计算。

7.2.2本章重难点例题讲解【例题1】一机器作稳定运动，其中一个运动循环中的等效阻力矩Mr 与等效驱动力矩Md 的变化线如图所示。

2.2.1 在平面机构中，两构件之间以线接触所组成的平面运动副，称为高副，它引入1个约束，保留了2个自由度。

2.2.2平面运动副的最大约束数为2，最小约束数为1；引入一个约束的运动副为一级副，引入两个约束的运动副为二级副。

2.2.3构成机构的要素是构件和运动副；构件是机构中独立运动的单元体。

2.2.4在平面机构中，一个运动副引入约束的变化范围是1—2。

2.2.5以下几种常见的运动副中，其中（C）是高副。

A．滑动轴承B。

移动副C。

齿轮副D。

螺旋副2.2.6运动副中，凡是以点或线接触的，称为高副，而低副则是以面接触的。

2.2.7 构件是机械中独立的制造单元。

（错）2.2.8 B是构成机械的最小单元，也是制造机械时的最小单元A.机器B.零件C.构件D.机构2.2.9两构件组成运动副的必要条件是两构件（A）A.直接接触且具有相对运动B。

直接接触但无相对运动C.虽然不接触但有相对运动D.既不接触也无相对运动2.2.10平面高副连接的两个构件间，只允许有相对滑动。

（错）2.2.11用平面低副连接的两构件间，具有相对运动的数目是3_ ？2.2.12具有一个自由度的运动副称为I级副。

（错）2.2.13 何为运动副？按接触形式分为几种？其自由度、约束数如何？答案：由两构件直接接触而组成的可动的连接；可分为高副和低副；2.3机构自由度的计算2.31机构组成原理是什么？答案：任何机构都是可以看作是由若干个基本杆组依次连接于原动件和机架上构成的。

2.3.2机构具有确定运动的条件是？答案：原动件的数目应等于该机构的自由度的数目2.3.3计算机构自由度时，若记入虚约束，则机构自由度的数目将（C）A.增大B.不变C.减少D.以上都有可能2.3.4机构中原动件数应等于机构的自由度数（对）2.3.5机构的自由度就是构件的自由度（错）2.3.6既然虚约束对机构的运动实际上不起约束作用，为什么在实际机械中又常常存在虚约束？答案：为了保证连杆运动的连续性2.3.7只有自由度为1的机构才具有确定的运动（对）2.3.8由M个构件组成的复合铰链应包括（M-1）个运动副2.3.9门与门框通常有两个以上的铰链，这是复合铰链的典型例子。

第七章 转子速度波动的调节一. 考点提要1. 主轴的角速度在经过一个运动周期之后又变回到初始状态，其平均角速度是一个常数，这种角速度的波动称为周期性速度波动。

２. 速度周期性波动的原因是，在整个周期中，驱动力作功与阻力作功总量相等，没有动能的持续增减，因此平均角速度不变。

但是在某个阶段，驱动力作功与阻力作功是不相等的，有动能的增加或减少，因此出现了角速度的变化。

３. 平均角速度是最大角速度和最小角速度的算术平均值： 2minmaxm （７－１）４. 速度不均匀系数是衡量速度波动程度的量，其值为：mminmax（７－２）５.周期性速度波动的调节方法是在机械上安装一个转动惯量比较大的回转构件―――飞轮。

当驱动功大于阻力作功的期间，多余的动能储存在飞轮中，使转速随动能的增加而增加，驱动功比阻力功大的部分称盈功。

当驱动功小于阻力作功的期间，储存在飞轮中的动能维持构件继续转动，使转速随动能的降低而降低。

驱动功小于阻力功的不足部分称亏功。

最大动能和最小动能的差值称最大盈亏功max A ，数值上等于动能的最大变化量E 。

)(212min2max maxH A E把（７－１）（７－２）代入得：][900][22max2max n A A J m（７－３） 式中：min /;/r n s rad m 是是平均角速度 6. 等效力和等效力矩在机械系统运动工作中，某个构件的瞬时功率为：i si i i i i v F M P cos式中的i M 代表标号为第i 的任意一个构件所受力矩；i 代表第i 个任意构件的角速度；i F 代表第i 个构件的受力；si v 代表第i 个构件质心的线速度；i 为第i 个构件受力方向与质心速度方向的夹角。

则整个系统的瞬时功率为：ni i si i n i i i v F M P 11cos用作用在某个构件上的等效力矩代替所有的力和力矩，其瞬时功率应相等，所以有：ni isi i ni ii e v F M M 11cos(7—4)用作用在某个构件上的等效力代替所有的力和力矩，同理有：ni isii ni i i e v v F v M F 11cos (7—5) 6.等效质量和等效转动惯量在机械系统中任意一个构件的动能为：222121si i i si i v m J E式中的si J 代表标号为第i 的任意一个构件对其质心的转动惯量；i 代表第i 个任意构件的角速度；i m 代表第i 个构件的质量；si v 代表第i 个构件质心的线速度；E i 代表第i 个构件的动能。

机械原理习题及答案要点机械原理习题及答案要点和；构件是机构中的单元体。

2、具有、、等三个特征的构件组合体称为机器。

3、从机构结构观点来看，任何机构是由三部分组成。

4、运动副元素是指。

5、构件的自由度是指；机构的自由度是指。

6、两构件之间以线接触所组成的平面运动副，称为副，它产生个约束，而保留个自由度。

7、机构具有确定的相对运动条件是原动件数机构的自由度。

8、在平面机构中若引入一个高副将引入______个约束，而引入一个低副将引入_____个约束，构件数、约束数与机构自由度的关系是。

9、平面运动副的最大约束数为，最小约束数为。

10、当两构件构成运动副后，仍需保证能产生一定的相对运动，故在平面机构中，每个运动副引入的约束至多为，至少为。

11、计算机机构自由度的目的是______。

12、在平面机构中，具有两个约束的运动副是副，具有一个约束的运动副是副。

13、计算平面机构自由度的公式为Ｆ=，应用此公式时应注意判断：(A)铰链，(B)自由度，(C)约束。

14、机构中的复合铰链是指；局部自由度是指；虚约束是指。

15、划分机构的杆组时应先按的杆组级别考虑，机构的级别按杆组中的级别确定。

16、图示为一机构的初拟设计方案。

试：(1〕计算其自由度，分析其设计是否合理？如有复合铰链，局部自由度和虚约束需说明。

(2)如此初拟方案不合理，请修改并用简图表示。

题16图题17图17、在图示机构中，若以构件1为主动件，试：(1)计算自由度，说明是否有确定运动。

(2)如要使构件6有确定运动，并作连续转动，则可如何修改？说明修改的要点，并用简图表示。

18、计算图示机构的自由度，将高副用低副代替，并选择原动件。

19、试画出图示机构的运动简图，并计算其自由度。

对图示机构作出仅含低副的替代机构，进行结构分析并确定机构的级别。

题19图题20图20、画出图示机构的运动简图。

21、画出图示机构简图，并计算该机构的自由度。

构件3为在机器的导轨中作滑移的整体构件，构件2在构件3的导轨中滑移，圆盘1的固定轴位于偏心处。