湖南师范大学附属中学2015届高三上学期月考(二)历史试题(扫描版)
- 格式:doc
- 大小:5.10 MB
- 文档页数:10

大联考湖南师大附中2025届高三月考试卷(一)历史时量:75分钟满分:100分第I卷选择题(共48分)一、选择题(本大题共16小题,每小题3分,共48分。
在每小题列出的四个选项中,只有一项是符合题意的)1.岭南石峡遗址已发掘64座大小不一的墓葬,出土遗物三千余件。
有出七成套的木作工具石锛和石凿,数百件实战用的石镞、石钺;还有礼器如琮、璧等,玉琮与良渚一带相近。
据此可推断,该遗址A.已出现掌握贵重礼器的祭司阶层B.处于石器时代向国家迈进的阶段C.有直接或间接远距离的商品交换D.农业生产水平得到一定程度发展2.图1、2所示文物均被学界命名为“蜻蜓眼玻璃器”。
据此可知图1古埃及玻璃器(前+4世纪)图2曾侯乙墓玻璃器(战国)A.社会分工发生了进一步细化B.战国手工制造水平超过古埃及C.玻璃器的生产中心发生转移D.玻璃器是中外文明交流的物证3.《史记·儒林列传》记载,“家人子”(宫侍女)出身的窦太后喜好黄老之学,召辕固生问老子书,辕固生答“家人言耳”太后大怒,命他去刺野猪,幸得景帝帮助才脱困。
这一记载最能印证汉初A.无为而治思想发生动摇B.弃道崇儒思想开始抬头C.社会等级意识仍然强烈D.皇权独尊遭受外戚挑战4.王莽改制,根据周朝办法造大钱,后又相继发行契刀、错刀、宝货等货币,民间仍用五铢钱。
王莽下诏:“敢非井田、挟五铢钱者为惑众,投诸四裔以御魑魅。
”可见当时A.制度变革获得法律保障B.币制由复杂走向简单C.托古改制重视民众基础D.政府的货币信用不足5.《公羊传》记载:“桓何以贵?母贵也。
母贵则子何以贵?子以母贵,母以子贵。
”然而汉武帝却在立幼子为太子后杀其生母,北魏时期道武帝将子贵母死立为定制。
这一转变的目的在于A.提高三纲五常的地位B.促进华夏认同C.推动少数民族封建化D.加强集权统治6.唐太宗审查《氏族志》时,认为山东崔氏“世代衰微,全无冠盖”,不配第一等。
他指示“不须论数世以前,止取今日官爵高下作等级”,新修订的《氏族志》以皇族为首,外戚次之,崔干被降为第三等。

2025届师大附中高三月考化学试卷(一)本试题卷分选择题和非选择题两部分,共10页。
时量75分钟,满分100分。
可能用到的相对原子质量:H:1 C:12 O:16 Sb:122一、选择题:本题共14小题,每小题3分,共42分。
每小题只有一个选项符合题目要求。
1. 化学与生活、生产密切相关,下列说法正确的是A. “酒香不怕巷子深”体现了熵增的原理B. 船体上镶嵌锌块,是利用外加电流法避免船体遭受腐蚀C. 烟花发出五颜六色的光是利用了原子的吸收光谱D. “太阳翼”及光伏发电系统能将太阳能变为化学能2. 下列化学用语或化学图谱不正确的是NH的VSEPR模型:A. 3CH CH OCH CHB. 乙醚的结构简式:3223C. 乙醇的核磁共振氢谱:D. 邻羟基苯甲醛分子内氢键示意图:3. 实验室中,下列实验操作或事故处理不合理的是A. 向容量瓶转移液体时,玻璃棒下端应在容量瓶刻度线以下B. 苯酚不慎沾到皮肤上,先用抹布擦拭,再用65C°水冲洗C. 用二硫化碳清洗试管内壁附着的硫D. 对于含重金属(如铅、汞或镉等)离子的废液,可利用沉淀法进行处理4. 下列有关有机物的说法正确的是A. 聚乙烯塑料的老化是由于发生了加成反应B. 二氯丁烷的同分异构体为8种(不考虑立体异构)C. 核酸可视为核苷酸的聚合产物D. 乙醛和丙烯醛()不是同系物,它们与氢气充分反应后的产物也是同系物5. 下列反应方程式书写不正确的是A. 将223Na S O 溶液与稀硫酸混合,产生浑浊:2-+2322S O +2H =SO +S +H O ↑↓B. 用浓氨水检验氯气泄漏:32428NH +3Cl =6NH Cl+NC. 稀硫酸酸化的淀粉-KI 溶液在空气中放置一段时间后变蓝:-2-+42222I +SO +4H =I +SO +2H O ↑D. ()32Ca HCO 溶液与少量NaOH 溶液反应:-2+-332HCO +Ca +OH =CaCO +H O ↓6. 内酯Y 可以由X 通过电解合成,并可在一定条件下转化为Z ,转化路线如图所示。
湖南师大附中2025届高三月考试卷(三)历史审题人:高三历史备课组时量:75分钟满分:100分得分第Ⅰ卷选择题(共48分)一、选择题(本大题共16小题,每小题3分,共48分。
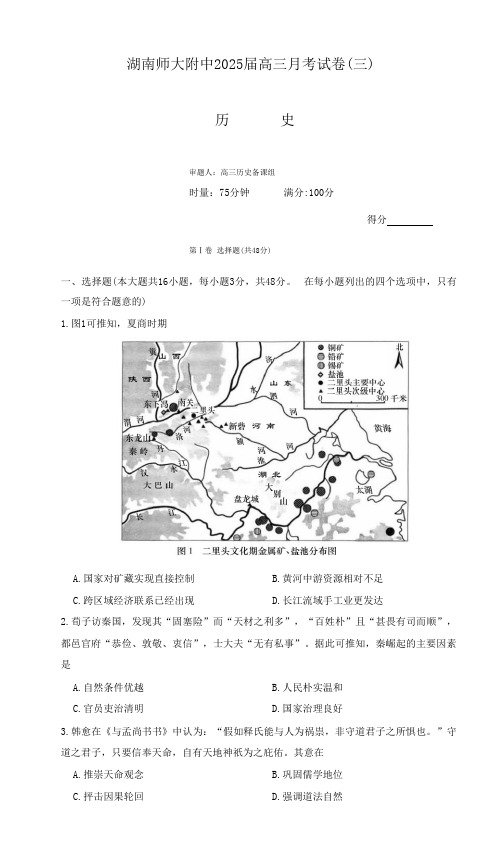
在每小题列出的四个选项中,只有一项是符合题意的)1.图1可推知,夏商时期A.国家对矿藏实现直接控制B.黄河中游资源相对不足C.跨区域经济联系已经出现D.长江流域手工业更发达2.荀子访秦国,发现其“固塞险”而“天材之利多”,“百姓朴”且“甚畏有司而顺”,都邑官府“恭俭、敦敬、衷信”,士大夫“无有私事”。
据此可推知,秦崛起的主要因素是A.自然条件优越B.人民朴实温和C.官员吏治清明D.国家治理良好3.韩愈在《与孟尚书书》中认为:“假如释氏能与人为祸祟,非守道君子之所惧也。
”守道之君子,只要信奉天命,自有天地神祇为之庇佑。
其意在A.推崇天命观念B.巩固儒学地位4.辽朝的国号变迁复杂。
建国之初称大契丹,辽太宗时期实行双重国号(燕云汉地称大辽,草原地区称大契丹);后多次在大辽和契丹中复改国号。
这体现出辽A.疆域版图不断变迁B.政治体制的二元性C.民族交融逐渐加深D.内外政策左右摇摆5.明朝中后期,有史料记载“无籍之徒”日渐猖獗,“投托权豪势要之家,充为家人伴当”,“不务本等生业,三五成群,白昼在街撒泼、殴打平人、抢夺财物”。
这一群体A.加剧了土地兼并的矛盾B.有利于人身依附的放松C.推动了社会阶层的流动D.削弱了政府的行政效力6.1898年,湖广总督张之洞主编《劝学篇》一书,在序言中写道:“学者摇摇,中无所主,邪说暴行,横流天下……吾恐中国之祸,不在四海之外,而在九州之内矣。
”《劝学篇》的指向是A.纠正维新派理论中的偏颇之处B.为康梁变法革新运动造势C.抨击顽固派学者们的保守论调D.为光绪帝看世界提供帮助7.湖南手工业向称发达。
然而20世纪初,时人“欲求一匹真土纱织布,几如披沙拣金”;大批手工业者被抛入城市,正业之农耕变成副业,副业的苦力变成正业。

湖南省长沙市湖南师大附中2025届高三月考试卷(三)语文试题本试卷共四道大题,23道小题,满分150分。
时量150分钟。
得分:_一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
对于大部分人来说,隐喻不是寻常的语言,而是诗意的想象和修辞多样性的一种策略,非同寻常。
而且,隐喻通常被看成语言文字的特征,而非思想和行为的特点。
由于这个原因,大多数人认为没有隐喻的存在,他们依然可以自如地生活,而我们发现事实恰恰相反。
不论是在语言上还是在思想和行动中,日常生活中隐喻无所不在,我们思想和行为所依据的概念系统本身是以隐喻为基础。
这些支配着我们思想的概念不仅关乎我们的思维能力,它们也同时管辖我们日常的运作,乃至一些细枝末叶的平凡细节。
这些概念建构了我们的感知,构成了我们如何在这个世界生存以及我们与其他人的关系。
因此,我们的这个概念系统在界定日常现实中扮演着举足轻重的角色。
我们的概念系统大部分是隐喻——如果我们说的没错的话,那么我们的思维方式,我们每天所经历所做的一切就充满了隐喻。
但是我们的概念系统不是我们平时能够意识到的。
我们每天所做的大部分琐事都只是按照某些方式或多或少地在自动思维和行动。
这些方式是什么却并非显而易见。
要搞清这些,一个方法就是研究语言。
既然交流是基于我们用以思考和行动的同一个概念系统,那么语言就是探明这个系统是什么样子的重要证据来源。
基于语言学证据(linguistic evidence),我们已经发现我们普通的概念系统,究其实质,大都是隐喻的,并且找到了一种方式来仔细鉴定那些建构我们如何感知、如何思考、如何行动的隐喻究竟是什么。
为了说明什么样的概念是隐喻,这样的概念又如何建构我们的日常活动,让我们从“争论”(ARGUMENT)以及“争论是战争”这个概念隐喻开始阐述吧。
日常生活中总是能见到这类表达:争论是战争你的观点无法防御。
他攻击我观点中的每一个弱点。

湖南省湖南师范大学附属中学2023-2024学年高三上学期月考(二)英语试卷本试题卷分为听力、阅读、语言运用和写作四个部分,共10页。
时量120分钟。
满分150分。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节 (共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.₤19.15.B.₤9.18.C.₤9.15.答案是C。
1.What does the man think of the price?A. It could be lower.B. It's low indeed.C. It's quite normal.2.What can we learn from the conversation?A.Tommy failed a game.B. Tommy broke his glasses.C. The window was broken.3. How should the woman pay?A. By check.B. With cash.C. By credit card.4.What midterm exams does the woman have?A. History and English.B. Chemistry and French.C. French and history.5. What does the man mean?A. The airplane is a better transport.B. The train can be an alternative.C. They won't get tickets.第二节 (共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。

炎德·英才大联考长郡中学2025届高三月考试卷(二)语文本试卷共四道大题,23道小题。
时量150分钟,满分150分。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成1~5题。
材料一:我们要理解中国传统的山水眼光,进而用这种眼光观看我们周围的真山真水。
什么是山水的眼光? 中国画家画一座山,通常先在山脚下住一段时间,在山腰又住一段时间,山前山后来回跑,又无数次登上山岭远望,最后整座山了然于心,待要画时,和盘托出。
一画之中,山脚与山体俱见,山前和山后齐观,巅顶与群峦并立,这就是所谓的“高远、深远、平远”。
不为透视所拘,不受视域所限,山水草木一例相看,烟云山壑腾挪反转。
古人把这种方法称为饱游而饫看,游目而骋怀。
山水眼光是一种不唯一时一侧的观看,更是将观看化入胸壑,化成天地综观的感性方式。
山止川行,风禾尽起。
中国人的内心始终有一种根深蒂固的山水依恋。
何谓“山”?山者,宣也。
宣气散,万物生。
山代表着大地之气的宣散,代表着宇宙生机的根源,故而山主生,呈现为一种升势。
何谓“水”? 水者,准也。
“上善若水,水善利万物而不争。
”相对山,水主德,呈现为平势、和势。
正是这种山水之势在开散与聚合之中,在提按与起落之中,起承转合,趋背相异,从而演练与展现出万物的不同情态、不同气韵。
山水非一物,山水是万物,它本质上是一个世界观,是一种关于世界的综合性的“谛视”。
所谓“谛视”,就是超越一个人瞬间感受的意念,依照生命经验之总体而构成的完整世界图景。
这种图景是山水的人文世界,是山水的“谛视”者将其一生的历练与胸怀置入山水云霭的聚散之中,将现实的起落、冷暖、抑扬、明暗纳入内心的观照之中,形成“心与物游”的存在。
多年前,我曾在台北故宫博物院欣赏北宋郭熙的《早春图》。
我在这里看到一片奇幻的山壑被一层层的烟云包裹着,宁静而悠远,峻拔而生机勃勃。
这是早春即将来临之时的山中景象——冬去春来,大地苏醒,山间浮动着淡淡的雾气,传出春天的消息。
大联考湖南师大附中2025届高三月考试卷(一)数学命题人:高三数学备课组 审题人:高三数学备课组时量:120分钟 满分:150分一、选选选:本选共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,1. 已知{}()260,{lg 10}Axx x B x x =+−≤=−<∣∣,则A B = ( )A. {}32xx −≤≤∣ B. {32}x x −≤<∣ C. {12}x x <≤∣D. {12}x x <<∣2. 若复数z 满足()1i 3i z +=−+(i 是虚数单位),则z 等于( )A.B.54C.D.3. 已知平面向量()()5,0,2,1ab ==−,则向量a b +在向量b上投影向量为( )A. ()6,3−B. ()4,2−C. ()2,1−D. ()5,04. 记n S 为等差数列{}n a 的前n 项和,若396714,63a a a a +==,则7S =( ) A. 21B. 19C. 12D. 425. 某校高二年级下学期期末考试数学试卷满分为150分,90分以上(含90分)为及格.阅卷结果显示,全年级1200名学生的数学成绩近似服从正态分布,试卷的难度系数(难度系数=平均分/满分)为0.49,标准差为22,则该次数学考试及格的人数约为( )附:若()2,X Nµσ∼,记()()p k P k X k µσµσ=−≤≤+,则()()0.750.547,10.683p p ≈≈.A 136人 B. 272人C. 328人D. 820人6. 已知()π5,0,,cos ,tan tan 426αβαβαβ∈−=⋅=,则αβ+=( ) A.π6 B.π4C.π3D.2π37. 已知12,F F 是双曲线22221(0)x y a b a b−=>>的左、右焦点,以2F 为圆心,a 为半径的圆与双曲线的一条的.渐近线交于,A B 两点,若123AB F F >,则双曲线的离心率的取值范围是( )A.B.C. (D. (8. 已知函数()220log 0x a x f x x x ⋅≤= > ,,,,若关于x 的方程()()0f f x =有且仅有两个实数根,则实数a 的取值范围是( ) A. ()0,1B. ()(),00,1−∞∪C. [)1,+∞D. ()()0,11,+∞二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分9. 如图,在正方体111ABCD A B C D −中,E F M N ,,,分别为棱111AA A D AB DC ,,,的中点,点P 是面1B C 的中心,则下列结论正确的是( )A. E F M P ,,,四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN10. 已知函数()5π24f x x=+,则( )A. ()f x 的一个对称中心为3π,08B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象 C. ()f x 在区间5π7π,88上单调递增 D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点,则5π13π,24m∈11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++−=,则( )A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =−=∑ 三、填空题:本题共3小题,每小题5分,共15分.12. 6(31)x y +−的展开式中2x y 的系数为______.13. 已知函数()f x 是定义域为R 的奇函数,当0x >时,()()2f x f x ′−>,且()10f =,则不等式()0f x >的解集为__________.14. 已知点C 为扇形AOB 弧AB 上任意一点,且60AOB ∠=,若(),R OC OA OB λµλµ=+∈,则λµ+的取值范围是__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ,已知22cos a b c B +=. (1)求角C ;(2)若角C 的平分线CD 交AB于点,D AD DB =,求CD 的长.16. 已知1ex =为函数()ln af x x x =的极值点. (1)求a 的值; (2)设函数()ex kxg x =,若对()120,,x x ∀∈+∞∃∈R ,使得()()120f x g x −≥,求k 的取值范围. 17. 已知四棱锥P ABCD −中,平面PAB ⊥底面,ABCD AD∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥==为AB 的中点,F 为棱PC 上异于,P C 的点.的(1)证明:BD EF ⊥;(2)试确定点F 的位置,使EF 与平面PCD18. 在平面直角坐标系xOy 中,抛物线21:2(0)C ypx p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长,点P 在抛物线1C 上,圆222:(2)E x y r −+=(其中01r <<).(1)若1,2r Q =为圆E 上的动点,求线段PQ 长度的最小值; (2)设()1,D t 是抛物线1C 上位于第一象限的一点,过D 作圆E 的两条切线,分别交抛物线1C 于点,M N .证明:直线MN 经过定点.19. 龙泉游泳馆为给顾客更好的体验,推出了A 和B 两个套餐服务,顾客可选择A 和B 两个套餐之一,并在App 平台上推出了优惠券活动,下表是该游泳馆在App 平台10天销售优惠券情况. 日期t 12345678910销售量千张 1.9 1.98 2.2 2.36 2.43 2.59 2.68 2.76 2.7 04经计算可得:10101021111 2.2,118.73,38510i i i i i i i y y t y t ======∑∑∑ (1)因为优惠券购买火爆,App 平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,已知销售量y 和日期t 呈线性关系,现剔除第10天数据,求y 关于t 的经验回归方程结果中的数值用分数表示;(2)若购买优惠券的顾客选择A 套餐的概率为14,选择B 套餐的概率为34,并且A 套餐可以用一张优惠券,B 套餐可以用两张优惠券,记App 平台累计销售优惠券为n 张的概率为n P ,求n P ; (3)记(2)中所得概率n P 的值构成数列{}()N n P n ∗∈.①求n P 的最值;②数列收敛的定义:已知数列{}n a ,若对于任意给定的正数ε,总存在正整数0N ,使得当0n N >时,n a a ε−<,(a 是一个确定的实数),则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛...参考公式: ()()()1122211ˆˆ,n ni ii ii i n n i i i i x x y y x y nx yay bx x xx nx====−−−==−−−∑∑∑∑.大联考湖南师大附中2025届高三月考试卷(一)数学命题人:高三数学备课组 审题人:高三数学备课组时量:120分钟 满分:150分一、选选选:本选共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,1. 已知{}()260,{lg 10}Axx x B x x =+−≤=−<∣∣,则A B = ( )A. {}32xx −≤≤∣ B. {32}x x −≤<∣ C. {12}x x <≤∣ D. {12}x x <<∣【答案】D 【解析】【分析】通过解一元二次不等式和对数函数的定义域,求出集合,A B ,再求交集. 【详解】集合{}()32,{lg 10}{12}A x x B x x x x =−≤≤=−<=<<∣∣∣,则{12}A B xx ∩=<<∣, 故选:D .2. 若复数z 满足()1i 3i z +=−+(i 是虚数单位),则z 等于( )A.B.54C.D.【答案】C 【解析】【分析】由复数的除法运算计算可得12i z =−+,再由模长公式即可得出结果. 【详解】依题意()1i 3i z +=−+可得()()()()3i 1i 3i 24i12i 1i 1i 1i 2z −+−−+−+====−+++−,所以z =. 故选:C3. 已知平面向量()()5,0,2,1a b ==−,则向量a b +在向量b上的投影向量为( )A. ()6,3−B. ()4,2−C. ()2,1−D. ()5,0【答案】A 【解析】【分析】根据投影向量的计算公式即可求解.【详解】()()7,1,15,a b a b b b +=−+⋅==所以向量a b +在向量b 上的投影向量为()()236,3||a b b b bb +⋅==− .故选:A4. 记n S 为等差数列{}n a 的前n 项和,若396714,63a a a a +==,则7S =( ) A. 21 B. 19C. 12D. 42【答案】A 【解析】【分析】根据等差数列的性质,即可求解公差和首项,进而由求和公式求解.【详解】{}n a 是等差数列,396214a a a ∴+==,即67a =,所以67769,a a a a == 故公差76162,53d a a a a d =−=∴=−=−,()767732212S ×∴=×−+×=, 故选:A5. 某校高二年级下学期期末考试数学试卷满分为150分,90分以上(含90分)为及格.阅卷结果显示,全年级1200名学生的数学成绩近似服从正态分布,试卷的难度系数(难度系数=平均分/满分)为0.49,标准差为22,则该次数学考试及格的人数约为( )附:若()2,X Nµσ∼,记()()p k P k X k µσµσ=−≤≤+,则()()0.750.547,10.683p p ≈≈.A. 136人B. 272人C. 328人D. 820人【答案】B 【解析】【分析】首先求出平均数,即可得到学生的数学成绩2~(73.5,22)X N ,再根据所给条件求出(5790)P X ≤≤,即可求出(90)P X ≥,即可估计人数.【详解】由题得0.4915073.5,22µσ=×==,()()(),0.750.547p k P k X k p µσµσ=−≤≤+≈ ,()5790P X ∴≤≤ ()0.750.547p ≈,()()900.510.5470.2265P X ≥×−,∴该校及格人数为0.22651200272×≈(人),故选:B . 6. 已知()π5,0,,cos ,tan tan 426αβαβαβ∈−=⋅=,则αβ+=( ) A.π6 B.π4C.π3D.2π3【答案】D 【解析】【分析】利用两角差的余弦定理和同角三角函数的基本关系建立等式求解,再由两角和的余弦公式求解即可.【详解】由已知可得5cos cos sin sin 6sin sin 4cos cos αβαβαβαβ⋅+⋅=⋅ =⋅ , 解得1cos cos 62sin sin 3αβαβ⋅=⋅=,,()1cos cos cos sin sin 2αβαβαβ∴+=⋅−⋅=−,π,0,2αβ∈,()0,παβ∴+∈, 2π,3αβ∴+=,故选:D .7. 已知12,F F 是双曲线22221(0)x y a b a b−=>>的左、右焦点,以2F 为圆心,a 为半径的圆与双曲线的一条渐近线交于,A B 两点,若123AB F F >,则双曲线的离心率的取值范围是( )A.B.C. (D. (【答案】B 【解析】【分析】根据双曲线以及圆的方程可求得弦长AB =,再根据不等式123AB F F >整理可得2259c a <,即可求得双曲线的离心率的取值范围.【详解】设以()2,0F c 为圆心,a 为半径的圆与双曲线的一条渐近线0bx ay −=交于,A B 两点, 则2F 到渐近线0bx ay −=的距离d b,所以AB =, 因为123AB F F >,所以32c ×>,可得2222299a b c a b −>=+, 即22224555a b c a >=−,可得2259c a <,所以2295c a <,所以e <,又1e >,所以双曲线的离心率的取值范围是 .故选:B8. 已知函数()220log 0x a x f x x x ⋅≤= > ,,,,若关于x 的方程()()0f f x =有且仅有两个实数根,则实数a 的取值范围是( ) A. ()0,1 B. ()(),00,1−∞∪C. [)1,+∞D. ()()0,11,+∞【答案】C 【解析】【分析】利用换元法设()u f x =,则方程等价为()0f u =,根据指数函数和对数函数图象和性质求出1u =,利用数形结合进行求解即可. 【详解】令()u f x =,则()0f u =.�当0a =时,若()0,0u f u ≤=;若0u >,由()2log 0f u u==,得1u =. 所以由()()0ff x =可得()0f x ≤或()1f x =.如图所示,满足()0f x ≤的x 有无数个,方程()1f x =只有一个解,不满足题意;�当0a ≠时,若0≤u ,则()20uf u a =⋅≠;若0u >,由()2log 0f u u==,得1u =. 所以由()()0ff x =可得()1f x =,当0x >时,由()2log 1f x x==,可得2x =, 因为关于x 的方程()()0f f x =有且仅有两个实数根,则方程()1f x =在(,0∞−]上有且仅有一个实数根,若0a >且()(]0,20,xx f x a a ≤=⋅∈,故1a ≥; 若0a <且()0,20xx f x a ≤=⋅<,不满足题意.综上所述,实数a 的取值范围是[)1,+∞, 故选:C .二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分9. 如图,在正方体111ABCD A B C D −中,E F M N ,,,分别为棱111AA A D AB DC ,,,的中点,点P 是面1B C 的中心,则下列结论正确的是( )A. E F M P ,,,四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN【答案】BD 【解析】【分析】可得过,,E F M 三点的平面为一个正六边形,判断A ;分别连接,E F 和1,B C ,截面1C BEF 是等腰梯形,判断B ;分别取11,BB CC 的中点,G Q ,易证EF 显然不平行平面QGMN ,可判断C ;EM ⊥平面PMN ,可判断D.【详解】对于A :如图经过,,E F M 三点的平面为一个正六边形EFMHQK ,点P 在平面外,,,,E F M P ∴四点不共面,∴选项A 错误;对于B :分别连接,E F 和1,B C ,则平面PEF 即平面1C BEF ,截面1C BEF 是等腰梯形,∴选项B 正确;对于C :分别取11,BB CC 的中点,G Q ,则平面PMN 即为平面QGMN , 由正六边形EFMHQK ,可知HQ EF ,所以MQ 不平行于EF ,又,EF MQ ⊂平面EFMHQK ,所以EF MQ W = ,所以EF I 平面QGMN W =, 所以EF 不平行于平面PMN ,故选项C 错误;对于D :因为,AEM BMG 是等腰三角形,45AME BMG ∴∠=∠=°, 90EMG ∴∠=°,EMMG ∴⊥,,M N 是,AB CD 的中点,易证MN AD ∥,由正方体可得AD ⊥平面11ABB A ,MN ∴⊥平面11ABB A ,又ME ⊂平面11ABB A ,EM MN ∴⊥,,MG MN ⊂ 平面PMN ,EM ∴⊥平面GMN ,EM ⊂ 平面MEF ,∴平面MEF ⊥平面,PMN 故选项D 正确.���BD .10. 已知函数()5π24f x x=+,则( )A. ()f x 的一个对称中心为3π,08B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象 C. ()f x 在区间5π7π,88上单调递增 D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点,则5π13π,24m∈【答案】BD 【解析】【分析】代入即可验证A ,根据平移可得函数图象,即可由正弦型函数的奇偶性求解B ,利用整体法即可判断C ,由5πcos 24x+求解所以根,即可求解D.【详解】对于A ,由35π3π2π0848f =+×=≠,故A 错误;对于B ,()f x 的图象向右平移3π8个单位长度后得: 3π3π5ππ228842y f x x x x=−−++,为奇函数,故B 正确; 对于C ,当5π7π,88x∈时,则5π5π2,3π42x +∈ ,由余弦函数单调性知,()f x 在区间5π7π,88 上单调递减,故C 错误;对于D ,由()1f x =,得5πcos 24x+ππ4x k =+或ππ,2k k +∈Z , ()y f x =在区间()0,m 上与1y =有且只有6个交点,其横坐标从小到大依次为:ππ5π3π9π5π,,,,,424242, 而第7个交点的横坐标为13π4, 5π13π24m ∴<≤,故D 正确. 故选:BD11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++−=,则( )A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =−=∑ 【答案】ABC 【解析】【分析】根据函数奇偶性以及所满足的表达式构造方程组可得()()222f x f x ++−=,即可判断A 正确;利用对称中心表达式进行化简计算可得B 正确,可判断()g x 也是以8为周期的周期函数,即C 正确;根据周期性以及()()42f x f x ++=计算可得20241(42)2024k f k =−=∑,可得D 错误. 【详解】由题意()()()(),f x f x g x g x −=−=−,且()()()00,21g f x g x =++−=, 即()()21f x g x +−=①, 用x −替换()()21f x g x ++−=中的x ,得()()21f x g x −+=②, 由①+②得()()222f x f x ++−=, 所以()f x 的图象关于点(2,1)对称,且()21f =,故A 正确;由()()222f x f x ++−=,可得()()()()()42,422f x f x f x f x f x ++−=+=−−=−, 所以()()()()82422f x f x f x f x +=−+=−−= , 所以()f x 是以8为周期的周期函数,故B 正确; 由①知()()21g x f x =+−,则()()()()882121g x f x f x g x +=++−=+−=,故()()8g x g x +=,因此()g x 也是以8为周期的周期函数, 所以()()202400g g ==,C 正确;又因为()()42f x f x ++−=,所以()()42f x f x ++=, 令2x =,则有()()262f f +=,令10x =,则有()()10142,f f +=…, 令8090x =,则有()()809080942f f +=, 所以1012(2)(6)(10)(14)(8090)(8094)2222024f f f f f f ++++++=+++=个所以20241(42)(2)(6)(10)(14)(8090)(8094)2024k f k f f f f f f =−=++++++=∑ ,故D 错误.故选:ABC【点睛】方法点睛:求解函数奇偶性、对称性、周期性等函数性质综合问题时,经常利用其中两个性质推得第三个性质特征,再进行相关计算.三、填空题:本题共3小题,每小题5分,共15分.12. 6(31)x y +−的展开式中2x y 的系数为______. 【答案】180− 【解析】【分析】根据题意,由条件可得展开式中2x y 的系数为213643C C (1)⋅−,化简即可得到结果. 【详解】在6(31)x y +−的展开式中, 由()2213264C C 3(1)180x y x y ⋅⋅−=−,得2x y 的系数为180−. 故答案为:180−.13. 已知函数()f x 是定义域为R 的奇函数,当0x >时,()()2f x f x ′−>,且()10f =,则不等式()0f x >的解集为__________.【答案】()()1,01,−∪+∞ 【解析】【分析】根据函数奇偶性并求导可得()()f x f x ′′−=,因此可得()()2f x f x ′>,可构造函数()()2xf x h x =e并求得其单调性即可得()f x 在()1,+∞上大于零,在()0,1上小于零,即可得出结论. 【详解】因为()f x 为奇函数,定义域为R ,所以()()f x f x −=−,两边同时求导可得()()f x f x ′′−−=−,即()()f x f x ′′−=且()00f =,又因为当0x >时,()()2f x f x ′−>,所以()()2f x f x ′>. 构造函数()()2xf x h x =e,则()()()22x f x f x h x ′−′=e , 所以当0x >时,()()0,h x h x ′>在()0,∞+上单调递增,又因为()10f =,所以()()10,h h x =在()1,+∞上大于零,在()0,1上小于零, 又因为2e 0x >,所以()f x 在()1,+∞上大于零,在()0,1上小于零, 因为()f x 为奇函数,所以()f x 在(),1∞−−上小于零,在()1,0−上大于零, 综上所述,()0f x >的解集为()()1,01,−∪+∞. 故答案为:()()1,01,−∪+∞14. 已知点C 为扇形AOB 的弧AB 上任意一点,且60AOB ∠=,若(),R OC OA OB λµλµ=+∈,则λµ+的取值范围是__________.【答案】【解析】【分析】建系设点的坐标,再结合向量关系表示λµ+,最后应用三角恒等变换及三角函数值域求范围即可. 【详解】方法一:设圆O 的半径为1,由已知可设OB 为x 轴的正半轴,O 为坐标原点,过O 点作x 轴垂线为y 轴建立直角坐标系,其中()()1,1,0,cos ,sin 2A B C θθ ,其中π,0,3BOC θθ ∠=∈ , 由(),R OC OA OB λµλµ=+∈,即()()1cos ,sin 1,02θθλµ =+,整理得1cos sin 2λµθθ+=,解得cos λµθ=,则ππcos cos ,0,33λµθθθθθ+=++=+∈,ππ2ππ,,sin 3333θθ+∈+∈所以λµ +∈ . 方法二:设k λµ+=,如图,当C 位于点A 或点B 时,,,A B C 三点共线,所以1k λµ=+=; 当点C 运动到AB的中点时,k λµ=+,所以λµ +∈故答案为:四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ,已知22cos a b c B +=. (1)求角C ;(2)若角C 的平分线CD 交AB于点,D AD DB =,求CD 的长.【答案】(1)2π3C = (2)3CD = 【解析】【分析】(1)利用正弦定理及两角和的正弦定理整理得到()2cos 1sin 0C B +=,再利用三角形的内角及正弦函数的性质即可求解;(2)利用正弦定理得出3b a =,再由余弦定理求出4a =,12b =,再根据三角形的面积建立等式求解. 【小问1详解】 由22cos a b c B +=,根据正弦定理可得2sin sin 2sin cos A B C B +=,则()2sin sin 2sin cos B C B C B ++=,所以2sin cos 2cos sin sin 2sin cos B C B C B C B ++=,整理得()2cos 1sin 0C B +=, 因为,B C 均为三角形内角,所以(),0,π,sin 0B C B ∈≠, 因此1cos 2C =−,所以2π3C =. 【小问2详解】因为CD 是角C的平分线,AD DB=所以在ACD 和BCD △中,由正弦定理可得,,ππsin sin sin sin 33AD CD BD CDA B ==, 因此sin 3sin BADA BD==,即sin 3sin B A =,所以3b a =, 又由余弦定理可得2222cos c a b ab C =+−,即222293a a a =++, 解得4a =,所以12b =.又ABCACD BCD S S S =+△△△,即111sin sin sin 222ab ACB b CD ACD a CD BCD ∠∠∠=⋅⋅+⋅⋅, 即4816CD =,所以3CD =. 16. 已知1ex =为函数()ln af x x x =的极值点. (1)求a 的值; (2)设函数()ex kxg x =,若对()120,,x x ∀∈+∞∃∈R ,使得()()120f x g x −≥,求k 的取值范围. 【答案】(1)1a = (2)(]()10,−∞−+∞ , 【解析】【分析】(1)直接根据极值点求出a 的值;(2)先由(1)求出()f x 的最小值,由题意可得是求()g x 的最小值,小于等于()f x 的最小值,对()g x 求导,判断由最小值时的k 的范围,再求出最小值与()f x 最小值的关系式,进而求出k 的范围. 【小问1详解】()()111ln ln 1a a f x ax x x x a x xα−−==′+⋅+,由1111ln 10e e e a f a −=+=′,得1a =, 当1a =时,()ln 1f x x =′+,函数()f x 在10,e上单调递减,在1,e∞ +上单调递增, 所以1ex =为函数()ln af x x x =的极小值点, 所以1a =. 【小问2详解】由(1)知min 11()e ef x f ==−. 函数()g x 的导函数()()1e xg x k x −=−′ �若0k >,对()1210,,x x k ∞∀∈+∃=−,使得()()12111e 1e k g x g f x k=−=−<−<−≤,即()()120f x g x −≥,符合题意. �若()0,0kg x =,取11ex =,对2x ∀∈R ,有()()120f x g x −<,不符合题意.�若0k <,当1x <时,()()0,g x g x ′<在(),1∞−上单调递减;当1x >时,()()0,g x g x ′>在(1,+∞)上单调递增,所以()min ()1ekg x g ==, 若对()120,,x x ∞∀∈+∃∈R ,使得()()120f x g x −≥,只需min min ()()g x f x ≤, 即1e ek ≤−,解得1k ≤−. 综上所述,k 的取值范围为(](),10,∞∞−−∪+.17. 已知四棱锥P ABCD −中,平面PAB ⊥底面,ABCD AD ∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥==为AB 的中点,F 为棱PC 上异于,P C 的点.(1)证明:BD EF ⊥;(2)试确定点F 的位置,使EF 与平面PCD【答案】(1)证明见解析 (2)F 位于棱PC 靠近P 的三等分点 【解析】【分析】(1)连接,,PE EC EC 交BD 于点G ,利用面面垂直的性质定理和三角形全等,即可得证; (2)取DC 的中点H ,以E 为坐标原点,分别以,,EB EH EP 所在直线为,,x y z 轴建立,利用线面角公式代入即可求解.小问1详解】如图,连接,,PE EC EC 交BD 于点G .因为E 为AB 的中点,PA PB =,所以PE AB ⊥.因为平面PAB ⊥平面ABCD ,平面PAB ∩平面,ABCD AB PE =⊂平面PAB , 所以PE ⊥平面ABCD ,因为BD ⊂平面ABCD ,所以PE BD ⊥.因为ABD BCE ≅ ,所以CEB BDA ∠∠=,所以90CEB ABD ∠∠+= , 所以BD EC ⊥,因为,,PE EC E PE EC ∩=⊂平面PEC , 所以BD ⊥平面PEC .因为EF ⊂平面PEC ,所以BD EF ⊥. 【小问2详解】如图,取DC 的中点H ,以E 为坐标原点,分别以,,EB EH EP 所在直线为,,x y z 轴建立空间直角坐标系,【设2AB =,则2,1,BC AD PA PB ====则()()()()0,0,1,1,2,0,1,1,0,0,0,0P C D E −,设(),,,(01)F x y z PF PC λλ=<<, 所以()(),,11,2,1x y z λ−=−,所以,2,1x y z λλλ===−,即(),2,1F λλλ−.则()()()2,1,0,1,2,1,,2,1DC PC EF λλλ==−=−,设平面PCD 的法向量为(),,m a b c =,则00DC m PC m ⋅=⋅=,,即2020a b a b c += +−= ,,取()1,2,3m =−− , 设EF 与平面PCD 所成的角为θ,由cos θ=sin θ=.所以sin cos ,m EF m EF m EF θ⋅===整理得2620λλ−=,因为01λ<<,所以13λ=,即13PF PC = ,故当F 位于棱PC 靠近P 的三等分点时,EF 与平面PCD18. 在平面直角坐标系xOy 中,抛物线21:2(0)C ypx p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长,点P 在抛物线1C 上,圆222:(2)E x y r −+=(其中01r <<).(1)若1,2r Q =为圆E 上的动点,求线段PQ 长度的最小值;(2)设()1,D t 是抛物线1C 上位于第一象限的一点,过D 作圆E 的两条切线,分别交抛物线1C 于点,M N .证明:直线MN 经过定点.【答案】(1(2)证明见解析【解析】【分析】(1)根据椭圆的短轴可得抛物线方程2y x =,进而根据两点斜率公式,结合三角形的三边关系,即可由二次函数的性质求解,(2)根据两点坐标可得直线,MN DM 的直线方程,由直线与圆相切可得,a b 是方程()()()2222124240r x r x r −+−+−=的两个解,即可利用韦达定理代入化简求解定点. 【小问1详解】 由题意得椭圆的方程:221116y x +=,所以短半轴14b = 所以112242p b ==×=,所以抛物线1C 的方程是2y x =. 设点()2,P t t ,则111222PQ PE ≥−=−=≥, 所以当232ι=时,线段PQ . 【小问2详解】()1,D t 是抛物线1C 上位于第一象限的点,21t ∴=,且()0,1,1t D >∴设()()22,,,M a a N b b ,则: 直线()222:b a MN y a x a b a −−=−−,即()21y a x a a b −=−+,即()0x a b y ab −++=. 直线()21:111a DM y x a −−=−−,即()10x a y a −++=. 由直线DMr =,即()()()2222124240r a r a r −+−+−=..同理,由直线DN 与圆相切得()()()2222124240r b r b r −+−+−=. 所以,a b 是方程()()()2222124240r x r x r −+−+−=的两个解, 22224224,11r r a b ab r r −−∴+==−− 代入方程()0x a b y ab −++=得()()222440x y r x y +++−−−=, 220,440,x y x y ++= ∴ ++= 解得0,1.x y = =− ∴直线MN 恒过定点()0,1−.【点睛】圆锥曲线中定点问题的两种解法(1)引进参数法:先引进动点的坐标或动线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点.(2)特殊到一般法:先根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关.技巧:若直线方程为()00y y k x x −=−,则直线过定点()00,x y ;若直线方程为y kx b =+ (b 为定值),则直线过定点()0,.b 19. 龙泉游泳馆为给顾客更好的体验,推出了A 和B 两个套餐服务,顾客可选择A 和B 两个套餐之一,并在App 平台上推出了优惠券活动,下表是该游泳馆在App 平台10天销售优惠券情况. 日期t 1 2 3 4 5 6 7 8 9 10 销售量千张 1.9 1.98 2.2 2.36 2.43 259 2.68 2.76 2.7 0.4经计算可得:10101021111 2.2,118.73,38510i i i i i i i y y t y t ======∑∑∑. (1)因为优惠券购买火爆,App 平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,已知销售量y 和日期t 呈线性关系,现剔除第10天数据,求y 关于t 的经验回归方程结果中的数值用分数表示;..(2)若购买优惠券的顾客选择A 套餐的概率为14,选择B 套餐的概率为34,并且A 套餐可以用一张优惠券,B 套餐可以用两张优惠券,记App 平台累计销售优惠券为n 张的概率为n P ,求n P ;(3)记(2)中所得概率n P 的值构成数列{}()Nn P n ∗∈. ①求n P 的最值;②数列收敛的定义:已知数列{}n a ,若对于任意给定的正数ε,总存在正整数0N ,使得当0n N >时,n a a ε−<,(a 是一个确定的实数),则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛.参考公式: ()()()1122211ˆˆ,n ni ii i i i n n ii i i x x y y x y nx y ay bx x x x nx ====−−−==−−−∑∑∑∑. 【答案】(1)673220710001200y t + (2)433774n n P =+⋅−(3)①最大值为1316,最小值为14;②证明见解析 【解析】 【分析】(1)计算出新数据的相关数值,代入公式求出 ,ab 的值,进而得到y 关于t 的回归方程; (2)由题意可知1213,(3)44n n n P P P n −−=+≥,其中12113,416P P ==,构造等比数列,再利用等比数列的通项公式求解;(3)①分n 为偶数和n 为奇数两种情况讨论,结合指数函数的单调性求解;②利用数列收敛的定义,准确推理、运算,即可得证. 【小问1详解】 解:剔除第10天的数据,可得2.2100.4 2.49y ×−==新, 12345678959t ++++++++=新, 则9922111119.73100.4114,73,38510285i i i i t y t = =−×==−= ∑∑新新,所以912922119114,7395 2.4673ˆ2859560009i i i i t y t y b t t == − −×× ==−× − ∑∑新新新新新, 可得6732207ˆ 2.4560001200a =−×=,所以6732207ˆ60001200y t +. 【小问2详解】 解:由题意知1213,(3)44n n n P P P n −−=+≥,其中12111313,444416P P ==×+=, 所以11233,(3)44n n n n P P P P n −−−+=+≥,又由2131331141644P P ++×, 所以134n n P P − +是首项为1的常数列,所以131,(2)4n n P P n −+=≥ 所以1434(),(2)747n n P P n −−=−−≥,又因为1414974728P −=−=−, 所以数列47n P − 是首项为928−,公比为34−的等比数列, 故1493()7284n n P −−=−−,所以1934433()()2847774n n n P −=−−+=+−. 【小问3详解】 解:①当n 为偶数时,19344334()()28477747n n n P −=−−+=+⋅>单调递减, 最大值为21316P =; 当n 为奇数时,19344334()()28477747n n n P −=−−+=−⋅<单调递增,最小值为114P =, 综上可得,数列{}n P 的最大值为1316,最小值为14. ②证明:对任意0ε>总存在正整数0347[log ()]13N ε=+,其中 []x 表示取整函数, 当 347[log ()]13n ε>+时,347log ()34333333()()()7747474n n n P εε−=⋅−=⋅<⋅=, 所以数列{}n P 收敛.【点睛】知识方法点拨:与新定义有关的问题的求解策略:1、通过给出一个新的定义,或约定一种新的运算,或给出几个新模型来创设新问题的情景,要求在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实心信息的迁移,达到灵活解题的目的;2、遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使得问题得以解决.方法点拨:与数列有关的问题的求解策略:3、若新定义与数列有关,可得利用数列的递推关系式,结合数列的相关知识进行求解,多通过构造的分法转化为等差、等比数列问题求解,求解过程灵活运用数列的性质,准确应用相关的数列知识.。
湖南师大附中2025届高三月考试卷(一)地理得分:______本试题卷分选择题和非选择题两部分,共8页。
时量75分钟,满分100分。
第Ⅰ卷选择题(共48分)一、选择题(本大题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求)职住关系是指居住地与工作地的空间位置关系,下图为城郊轨道交通沿线两种职住关系模式图。
完成下面小题。
1. 极化型职住关系主要反映了轨道交通沿线()A. 交通方式多样B. 逆城市化严重C. 生产要素集中D. 居住用地短缺2. 与极化型相比,平衡型职住关系的突出优点是()①减缓就业型站点的拥堵②强化中心城区核心地位③缩短职工平均通勤时间④人口趋向轨道沿线集聚A. ①③B. ①④C. ②③D. ②④加车村位于贵州省黔东南苗族侗族自治州,村庄依山而建,至今保留着诸如祭祀等完整的少数民族文化。
大、小芦笙堂是加车村重要的公共活动空间,其位置和功能有明显的差异。
随着乡村振兴战略的提出,加车村立足自身发展特点,积极打造商业街、扩建基础设施等,经济发展迅速。
下图示意加车村位置和村庄区位布局。
据此完成下面小题。
3. 在加车村可以见到的景象是( )A. 水满田畴的梯田B. 漫山遍野的牦牛C. 静静流淌的小河D. 纵横交错的车道4. 与大芦笙堂相比较,推测小芦笙堂功能特点是多承担( )A. 大型祭祀及休闲、娱乐活动B. 大型祭祀及农事、商贸活动C. 小型祭祀及休闲、娱乐活动D. 小型祭祀及农事、商贸活动5. 适于加车村发展的方向是( )A. 加快人口聚集,提高城镇化水平B. 促进村庄生产、生活、生态融合 C 下寨建筑集中连片,拓展商业街 D. 协调第一、二、三产业均衡发展 下图为2024年元旦跨年时刻江苏某同学查询到的太阳和月亮高度轨迹示意图,该同学在元旦(农历二十)日出时刻观察到了日、月同天景象。
据此回答下面小题。
6. 跨年钟声响起时,东半球新年的范围占全球的( )A. 5/6B. 2/9C. 1/6D. 1/97. 该同学观察到的日、月同天景象位置示意图是( )A. B. C.D.倒暖锋是我国东北地区的一种特殊天气类型,一般出现在强寒潮过境2~3天后。
湖南师大附中2025届高三月考试卷(三)历史参考答案一、选择题(本大题共16小题,每小题3分,共48分)题号12345678910111213141516答案C D B B D A A A B D C A C B C B1. C【解析】题中显示夏商时期早期金属矿、盐池的分布情况,政治中心在黄河中游,金属矿多分布于长江流域。
矿藏分布跨越南北方,这在一定程度上能够表明南北方之间可能因为资源的开发和利用存在着经济方面的联系,C项“跨区域经济联系已经出现”较为合理。
仅从图中所给的矿藏分布情况,无法直接得出“国家对矿藏实现直接控制”的结论,没有相关明确证据支持,A项错误。
从图中可以看到黄河中游有一定的矿藏分布,不能得出资源相对不足的结论,B项错误。
图中只是展示了矿藏的分布,并没有直接体现出手工业发达程度的比较,不能仅依据矿藏分布就得出“长江流域手工业更发达”的结论,D项错误。
2. D【解析】题干中提到秦国“圆塞险”而“天材之利多”,这只是自然条件方面的优势,但不是最主要因素;“百姓朴”且“甚畏有司而顺”说明百姓朴实且顺从管理;都邑官府“恭俭、敦敬、衷信”,士大夫“无有私事”,这些都体现了秦国在国家治理方面,官员清正廉洁、百姓顺从,整个国家治理良好。
A项自然条件优越只是一方面;B项人民朴实温和也只是一个方面;C项官员吏治清明也只是国家治理的一部分。
只有D项国家治理良好能够全面概括题干中所体现的泰国的优势。
3. B【解析】根据材料,韩愈认为:如果佛有灵,能给人带来灾祸,坚守儒道的君子只要信奉天命,就不用惧怕。
根据所学知识可知,韩愈提倡复兴儒学,他用天命观反对佛教的因果轮回,以巩固儒学地位,故B项正确。
A、C两项均为手段而非目的,故排除;材料中的“道”为儒道,而非道家思想,故D项错误。
4. B【解析】辽朝以契丹为国号,体现其对游牧民族传统和文化的重视;以辽为国号,体现其吸收汉文化和制度的意图;实行双重国号是要在保持游牧民族的传统和吸收汉文化中寻求平衡。
炎德·英才大联考湖南师大附中2025届高三月考试卷(二)地理本试题卷分选择题和非选择题两部分,共8页。
时量75分钟,满分100分。
第I 卷选择题(共48分)一、选择题(本大题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求)宁夏西海固是国家重点扶贫区域,该区域生态环境差,贫困人口多,扶贫措施以生态移民为主,北部闽宁镇成为移民首选地。
通过生态移民,西海固成功实现脱贫,闽宁产业也实现了多元化,主要以菌类、葡萄酒、光伏、电子装配等为主。
下图是西海固、闽宁镇区位略图。
据此完成下面小题。
1. 生态移民对西海固的积极意义是( )A. 优化居住条件B. 改善人口结构C. 减轻生态压力D. 增加劳务收入2. 闽宁成为移民首选地的自然因素是( )A 地形和水源 B. 地形和降水 C. 气温和水源 D. 气温和降水3. 闽宁实现产业多元化的有利条件是( )①自然环境优美②劳动力数量多③产业协作基础好④银川辐射作用强A. ①③B. ①④C. ②③D. ②④【答案】1. C2. A3. D 【解析】【1题详解】生态移民是将生态环境严重破坏地区的部分人口迁出,从而减轻生态压力,C 项正确;生态移民可以改善迁移者的居住条件,但不是能改善西海固的居住条件,A错误;生态移民为整体搬迁,对人口结构影响较.小,B错误;不会增加西海固的劳务收入,D错误。
所以选C。
【2题详解】闽宁地形平坦,有黄河经过,因此闽宁成为移民首选地的自然因素是地形和水源,A正确;该地降水较少,B错误;区域气温差异较小,气温不是影响移民的主要因素,CD错误。
所以选A。
【3题详解】自然环境不是影响产业多元化的主要因素,①错误;闽宁接收生态移民,获得大量劳动力,②正确;闽宁经济发展水平较低,产业协作基础较差,③错误;距离银川较近,受银川的辐射作用较强,④正确。
所以选D。
【点睛】生态移民亦称环境移民系指原居住在自然保护区、生态环境严重破坏地区、生态脆弱区以及自然环境条件恶劣、基本不具备人类生存条件的地区的人口,搬离原来的居住地,在另外的地方定居并重建家园的人口迁移。