07级第二学期复变函数与积分变换(A卷)

复变函数与积分变换期末考试试卷（A 卷）一、单项选择题(本大题共15小题，每小题2分，共30分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．下列复数中，位于第四象限的复数是（ ）A. 4+3iB. -3-3iC.-1+3iD.5-3i 2．下列等式中，不成立的等式是（ ） A. z·z =Re (z·z ).arg(3)arg()B i i -=- .rg(3)arg(3)C A =2.||D z z z ⋅=3．不等式 ||3z > 所表示的区域为（ ） A. 圆的外部B.上半平面C. 角形区域D.圆的内部4．积分||322z dz z =-⎰的值为（ ）A. 8i πB.2C. 2i πD. 4i π 5．下列函数中，在整个复平面上解析的函数是（ ）.z A z e +.sin z B z e + .tan z C z e + .R e ()s i n D z z+6．在复平面上，下列命题中，错误．．的是（ ）A. cosz 是周期函数B. ze 是解析函数.cos sin iz C e z i z =+.||D z =7．在下列复数中，使得ze =成立的是（ ）.ln 224iA z i ππ=++.ln 424iB z i ππ=++.ln 22C z i π=+.l n 42D z iπ=+ 8．设C 为正向圆周1||=z , 则积分 cos z c e dzz⎰等于（ ）A ．2πB ．2πiC ．0D ．－2π 9．设C 为正向圆周||2z =, 则21(1)C dz z i --⎰等于（ ）A.i21π B. 0 C.i 2πD.2i π-10．以下关于级数的命题不正确的是（ ）A.级数0327nn i ∞=+⎛⎫⎪⎝⎭∑是绝对收敛的B.级数212(1)n n in n ∞=⎛⎫+ ⎪-⎝⎭∑是收敛的 C.级数01(1)2n n n i n ∞=⎛⎫-+ ⎪⎝⎭∑是收敛的D.级数212n n i n ∞=⎛⎫+ ⎪⎝⎭∑是收敛的11．已知31z i =+，则下列正确的是（ ）12.iA z π=34.iB z eπ=712.i C z π=3.iD z π=12．下列关于幂级数的叙述，不正确 的是（ ） A.在收敛圆内，幂级数绝对收敛 B.在收敛圆外，幂级数发散 C.在收敛圆周上，可能收敛，也可能发散 D.在收敛圆周上，条件收敛13．0=z 是函数sin z e z z的（ ）A.本性奇点B.一级极点C.二级极点D.可去奇点14．cos z zz π-在点 z π= 处的留数为（ ） A. π-.B πC.1D. -115．关于0Im lim z zzω→=下列命题正确的是（ ）A.0ω=B. ω不存在C.1ω=-D.1ω=二、填空题（本大题共5小题，每小题2分，共10分）16.sincos 33z i ππ=+复数的三角形式为____________. 17. 已知22()()()f z x ay x i bxy y =++++在复平面上可导，则a b +=_________. 18. 设函数)(z f =3zt te dt ⎰，则)(z f 等于____________.19. 幂极数n n2n 1(-1)z n∞=∑的收敛半径为_______.20.设121,1z i z =-+=，求12z z ⎛⎫=⎪⎝⎭____________.三、计算题（本大题共4小题，每题7分，共28分） 21．设C 为从原点到2＋3i 的直线段，计算积分[(2)]CI x y ixy dz =-+⎰22. 设2()cos 4ze f z z z=+-. (1)求)(z f 的解析区域，（2）求).(z f '23. 将函数1()(1)(2)f z z z =--在点0=z 处展开为泰勒级数.24. 将函数112()(1)z ef z z -=-在圆环0|1|z <-<∞内展开成洛朗级数.四、综合题（共4小题，每题8分，共32分）25．已知22(,)2u x y x y x =-+，求一解析函数()(,)(,)f z u x y iv x y =+，并使(0)2f i =。

2007～2008学年第一学期《复变函数与积分变换》课程考试试卷(A 卷)院(系)_________专业班级__________学号_______________姓名__________考试日期: 2007年11月26日 考试时间: 晚上7:00~9:30题号 一 二 三 四 五 六 七 八 总分 得分一、填空题 (每空2分，共22分) 1．复数ii+-12的模为 ，辐角主值为 ． 2．函数22)(x i y z f -=在何处可导？ ， 何处解析？ ．3．2)3(Ln i +的值为 ． 4．函数iz i z z f ++-=)1(1)(2在0=z 点展开成泰勒(Taylor)级数的收敛半径为 ． 5．0=z 为函数2zzz f cos 1e )(-=的何种类型的奇点？ ．6．积分z z z zz d )2(sin 11||⎰=--的值为 ．7．映射z z z f 2)(2+=在i z -=处的伸缩率为 ， 旋转角为 ．8．函数t t f 2cos 21)(+=的Fourier 变换为 ．得 分 评卷人二、计算题 (每题5分，共20分)1．⎰=--2||2d )1(1e z z z z z2．⎰=2||12d 1sine z zz zz3．⎰-2π2cos d 05θθ得 分 评卷人4．x x xx d 2sin 0⎰∞++12三、(10分)已知y x a y x y x u 334),(+=，求常数a以及二元函数),(y x v ，使得v i u z f +=)(为 解析函数且满足条件0)1(=f ．得 分 评卷人四、(12分)将函数iz i z iz f ++--=)1(1)(2分别在 0=z 和1=z 处展开为洛朗(Laurent)级数．得 分 评卷人五、(8分)求区域}0Re ,2πIm 2π:{<<<-=z z z D 在映射iiw z z +-=e e 下的像．六、(10分)求把区域}0Re ,1|1|:{>>-=z z z D映射到单位圆内部的保形映射．得 分 评卷人得 分 评卷人七、(12分)利用Laplace 变换求解微分方程组：⎪⎩⎪⎨⎧='='-=-'-'===-''-''.1)0()0(,sin )()()(,0)0()0(,e )()()(y x t t x t y t x y x t t y t y t x t八、( 6 分)设函数)(z f 在2||<z 内解析，且满足2|2)(|<-z f ，证明：0d )(4)()(4)(1||2=-'-''⎰=z z f z f z f z f z ．得 分 评卷人得 分 评卷人。

07级复变函数与积分变换试卷湖南科技大学考试试题纸（A 卷）(2021 -2021 学年第二学期)复变函数与积分变换课程土木学院院（系） 06工程力学1-2 班级考试时量 100分钟学生人数 61 命题教师陈静系主任交题时间：年月日考试时间：年月日一、填空题（每空3分，共30分） 1. arg(?1?3i)= . 2．z?ii，则Rez= . 3. 设z?r(cos??isin?)，则zn?_________________. 4．积分|z|?1?z3edz＝ . 1z5. 函数sinz的周期为__________. 6. 设f(z)?1?cosz，则Res[f(z),0]= . 5zln(1?z)的奇点，其类型为 . z7.z?0是f(z)?8. 设u(x,y)的共轭调和函数为v(x,y)，那么v(x,y)的共轭调和函数为 . 9. f(z)?1在z?0处的泰勒展开式的收敛半径为 . 21?z10. 若f(t)?e?2t,则f(t)的Laplace变换为 . 二、选择题（每题4分，共20分） 1.下列结论不正确的是 . A. 若f(z)在z0解析，则f(z)在z0可导； B. 积分z?a?r?1dz的值与半径r(r?0)的大小无关; z?aC. 若在区域D内有f?(z)?g(z)，则在D内g?(z)存在且解析; D. 若f(z)在0?z?1内解析，且沿任何圆周c:z?r(0?r?1)的积分等于零，则f(z)在z?0处解析. 2.zk?1，其中k是非零整数，是的极点. k?A. 111； B. sinz；C. sin；D. . zsinz?1?sin???z?dz= . 22z?a 3.设C为正向圆周z?a?a(a?0)，则积分?A.?C?i2a B. ???ia C. ?i2aD. ?ia 4.级数?n?1e2?in 的收敛性为 . A. 通项趋于0，但发散 B.通项不趋于0 C. 条件收敛 D. 绝对收敛 5.设f(t)?cos?0t，则f(t)的Fourier变换为 . A. ?[?(???0)??(???0)] B. ?[?(???0)??(???0)] C. ?i[?(???0)??(???0)]D. ?i[?(???0)??(???0)] 三、计算（共50分） 1. 将函数f(z)?1分别在圆环域0?z?1?1和1?z?2???内展开成洛朗(z?1)(z?2)级数。

（完整）《复变函数与积分变换》期末考试试卷及答案,推荐⽂档23∞ ?复变函数与积分变换?期末试题（A）1．1 -i⼀．填空题（每⼩题3 分，共计15 分）的幅⾓是（）；2. Ln(-1 +i) 的主值是（1）；3.f (z) =1 +z 2，z - sin z f (5)(0) =（）；f (z) =1，4．z = 0 是z 4 的（）极点；5．z Re s[f(z),∞]=（）；⼆．选择题（每⼩题3 分，共计15 分）1．解析函数f (z) =u(x, y) +iv(x, y) 的导函数为（）；（A）f '(z) =u x +iu y ；（B）f '(z) =u x-iu y；（C） f '(z) =ux+ivy ；（D） f '(z) =u y +iv x.2．C 是正向圆周z = 3 ，如果函数f (z) =（），则?C f (z)d z = 0 ．3；（B）3(z -1)；（C）3(z -1)；（D）3.n=1（A）z =-2 点条件收敛；（B）z = 2i 点绝对收敛；（C）z = 1 +i 点绝对收敛；（D）z = 1 + 2i 点⼀定发散．４．下列结论正确的是( )（A）如果函数f (z) 在z0点可导，则f (z) 在z0点⼀定解析；得分e(B) 如果 f (z ) 在 C 所围成的区域内解析，则 ?C f (z )dz = 0（C ）如果 ?C f (z )dz = 0 ，则函数 f (z ) 在 C 所围成的区域内⼀定解析；（D ）函数 f (z ) = u (x , y ) + iv (x , y ) 在区域内解析的充分必要条件是u (x , y ) 、v (x , y ) 在该区域内均为调和函数． 5．下列结论不正确的是（）．(A) ∞为sin 1的可去奇点 z(B) ∞为sin z 的本性奇点 ∞为 1 的孤⽴奇点; ∞ 1 (C) sin 1z(D) 为的孤⽴奇点. sin z三．按要求完成下列各题（每⼩题 10 分，共计 40 分）（1）设 f (z ) = x 2 + axy + by 2 + i (cx 2 + dxy + y 2 ) 是解析函数，求a ,b ,c ,d .z（2）．计算 ?Cz (z - 1)2d z 其中 C 是正向圆周： z = 2 ；得分zd z （3）计算? 15z =3 (1 +z 2 )2 (2 +z 4 )3(sin z )3在扩充复平⾯上有什么类型的奇点？，如果有极点，请指出它的级.四、（本题 14 分）将函数 f (z ) = 1z 2 (z - 1)在以下区域内展开成罗朗级得分数；（1） 0 < z - 1 < 1 ，（2） 0 < z < 1 ，（3）1 < z < ∞五．（本题 10 分）⽤ Laplace 变换求解常微分⽅程定解问题 y (x ) - 5 y '(x ) + 4 y (x ) = e -xy (0) = y '(0) = 1得分六、（本题 6 分）求 f (t) e t(0) 的傅⽴叶变换，并由此证明：costt2 2 d 2 e 0复变函数与积分变换?期末试题（A ）答案及评分标准⼀．填空题（每⼩题 3 分，共计 15 分）得分3 的幅⾓是（ 2k Ln (-1 + i ) ee 1． 1- i 2 - + , k = 0,±1,±2 ）；2.的主值是（ 31 ln2 +3 24 iz - sin z f (z ) =3.1+ z 2 ， f(5)(0) = （ 0），4． z = 0 是1 z4的（⼀级）极点；5． f (z ) = z， R e s [ f (z ),∞] =（-1）；⼆．选择题（每题 3 分，共 15 分）1----5B DC B D三．按要求完成下列各题（每⼩题 10 分，共 40 分）（1）．设 f (z ) = x 2 + axy + by 2 + i (cx 2 + dxy + y 2 ) 是解析函数，求a ,b ,c ,d .解：因为 f (z ) 解析，由 C-R 条件u = vx y u = -vy x2x + ay = dx + 2y ax + 2by = -2cx - dy ,a = 2, d = 2, ， a = -2c ,2b = -d ,c = -1, b = -1,给出 C-R 条件 6 分，正确求导给 2 分，结果正确 2 分。

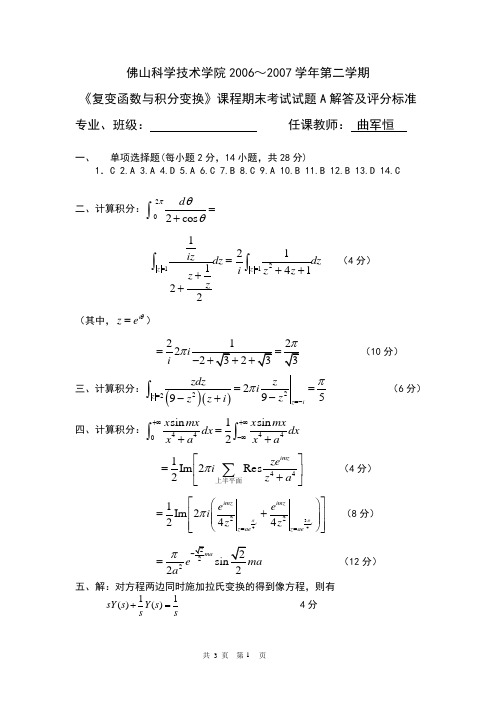
佛山科学技术学院2006～2007学年第二学期《复变函数与积分变换》课程期末考试试题A 解答及评分标准 专业、班级： 任课教师： 曲军恒一、 单项选择题(每小题2分，14小题，共28分)1．C 2.A 3.A 4.D 5.A 6.C 7.B 8.C 9.A 10.B 11.B 12.B 13.D 14.C二、计算积分：2 02cos d πθθ=+⎰11122z izdz z z ==++⎰212141z dz i z z =++⎰ （4分） （其中，i z e θ=）22i π==（10分） 三、计算积分：()()2222959z z izdz zi z z z i ππ==-==--+⎰ （6分）四、计算积分：44440sin 1sin 2x mx x mx dx dx x a x a+∞+∞-∞=++⎰⎰ 441Im 2Res 2imz ze i z a π⎡⎤=⎢⎥+⎣⎦∑上半平面 （4分） 344221Im 2244iiimz imzz ae z ae e e i z zπππ==⎡⎤⎛⎫=+⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎣⎦（8分）2sin22e ma aπ=（12分） 五、解：对方程两边同时施加拉氏变换的得到像方程，则有11()()sY s Y s s s+= 4分所以有21()1Y s s =+ 7分 对两边同时求拉氏逆变换得到()sin y t t = 10分 六、 当1z <时，111()(1)(2)(1)(2)f z z z z z ==-++++ 1111212z z =-++ （2分） 100(1)(1)2nnnnn n n z z ∞∞+===---∑∑101(1)12n n n n z ∞+=⎛⎫=-- ⎪⎝⎭∑ （5分） 当12z <<时，1111()12112f z z z z =-++ （7分） 11001(1)(1)2nnn n n n n zz ∞∞++===---∑∑ （10分）七、解：由柯西—黎曼条件， ()22222(*)x y x y u v xy-==+()2222(**)y x xyu v xy=-=+ （3分）由（**）式积分得 22()xu x x yϕ=-++，代入（*）式得()()2222222222()x y x y x xyxyϕ--'+=++，于是，()x C ϕ=，22xu C x y=-++ （6分） 22221()x y f z u iv C i C x y x y z=+=-+=-++ 代入(2)0f =，得2C =，因此， 11()2f z z=-。

二．判断题（每题3分，共30分） 1．n z z z f =)(在0=z 解读。

【 】2．)(z f 在0z 点可微，则)(z f 在0z 解读。

【 】 3．z e z f =)(是周期函数。

【 】4． 每一个幂函数在它的收敛圆周上处处收敛。

【 】 5． 设级数∑∞=0n n c 收敛，而||0∑∞=n n c 发散，则∑∞=0n n n z c 的收敛半径为1。

【 】6． 1tan()z能在圆环域)0(||0+∞<<<<R R z 展开成洛朗级数。

【 】 7． n 为大于1的正整数, Ln Ln n z n z =成立。

【 】 8．如果函数)(z f =ω在0z 解读，那末映射)(z f =ω在0z 具有保角性。

【 】9．如果u 是D 内的调和函数,则yu i x u f ∂∂-∂∂=是D 内的解读函数。

【 】10．212233||||221112|2(1)1z z z z dz dz i i z z z z ππ======--⎰⎰。

【 】 三．（8分）y e v px sin =为调和函数，求p 的值，并求出解读函数iv u z f +=)(。

四．（8分） 求())2)(1(--=z z zz f 在圆环域21<<z 和+∞<-<21z 内的洛朗展开式。

五．（8分）计算积分dx x x x ⎰∞+∞-++54cos 22。

六．（8分）设⎰-++=Cd zz f ξξξξ173)(2，其中C 为圆周3||=z 的正向，求(1)f i '+。

七．（8分）求将带形区域})Im(0|{a z z <<映射成单位圆的共形映射。

复变函数与积分变换(A)的参考答案与评分标准 (2007.7.5) 一.填空(各3分)1.3ln 2i k e +-π；2. 三级极点 ；3. 23z ；4. 0 ；5. 0 ；6.e1 ；7.322)1(26+-s s ；8. 0；9. 0 ；10. )]2()2()2(1)2(1[21++-+++-ωπδωπδωωj j 。

北 京 交 通 大 学2007-2008-2-《复变函数与积分变换A 》期末考试试卷(B)参考答案一．填空题（本题满分14分，每空1分），请将合适的答案填在空中.1．复数i i i z +-=2184，则=)Re(z _______；=)Im(z _______；=||z _______ =)arg(z ________________，复数z 的三角表达式为_____________________ 指数表达式为_______________________________________________________ 解：因为i i i i i i z 31414218-=+-=+-=所以，1)Re(=z ；3)Im(-=z ；10||=z ；3arctan )arg(-=z ， 复数z 的三角表达式为)]sin(arg )[cos(arg 10z i z +， 指数表达式为)arg(10z i e.2．方程083=+z 的所有根是2,1,0,28323==-=+k ez k iππ3．.,2,1,0,)1()]24(2[ln )1( ±±===++++k e ei k i i i iLn i ππ4．函数z ln 在复平面上的连续性为在除去原点和负实轴的平面上连续. 5．若幂级数∑∞=+1)(n nn i z c 在i z =处发散，则该级数在1=z 的敛敛性为发散6．映射ze w =将带形域43)Im(0π<<z 映照成角形域43)arg(0π<<z . 7．幂函数3z w =，把扇形域2||,3)arg(0<<<z z π映照为w 平面上的扇形域8||,)arg(0<<<z z π.8．在傅氏变换意义下，函数)(1t f 和)(2t f 的卷积)(*)(21t f t f 定义⎰+∞∞--τττd t ff )()(21.9．设)()(0t t t f -=δ，则)]([t f F =0t i eω-.二．判断下列命题的真假（本题满分10分，共有10道小题，每道小题1分），对的填“∨”，错的填“⨯”.（∨）1．指数函数ze 是以i π2为周期的周期函数. （⨯）2．正弦函数z sin 一定是有界函数. （⨯）3．奇点一定是孤立奇点.（⨯）4．)(z f 在0z 可导是)(z f 在0z 解析的充分条件.（∨）5．若u 和v 都是D 内的调和函数，且满足柯西-黎曼方程，则 iv u z f +=)(在区域D 内是解析函数.（⨯）6．若积分⎰=Cdz z f 0)(，C 是一条简单闭曲线，则)(z f 在C 内无奇点.（⨯）7．幂级数∑∞=1n nn z 的收敛半径为1，则在1||=z 上的点一定处处收敛.（⨯）8．函数y x v +=是y x u +=的共轭调和函数.（⨯）9．如果无穷远点∞是)(z f 的一阶极点，则0=z 是)1(zf 的一阶极点，并且)1(lim ]),([Re 0zzf z f s z →=∞.（⨯）10．映射2z w =在z 平面上每一点都具有伸缩率和旋转角的不变性.三．讨论函数33)1()(y i x z f -+=的可导性、解析性（8分）.解：设3x u =，3)1(y v -=，则v u ,处处可微且22)1(3,0,0,3y yvx v yu x x u --=∂∂=∂∂=∂∂=∂∂但1,00)1()1(332222==⇒=-+⇒--=⇒∂∂=∂∂y x y x y x yv x u即仅在点)1,0(处满足柯西-黎曼方程，因此，33)1()(y i x z f -+=在点)1,0(处可导，但在整个复平面上不解析.四．在扩充复平面上找出函数23)(23+-+=z z iz z f 的孤立奇点并加以分类，若是极点，指出其阶（或级）数，最后分别计算在每个孤立奇点的留数（8分）.解：)2)(1(23)(323--+=+-+=z z iz z z i z z f所以，)(z f 共有两个一阶极点2,121==z z 和一个无穷远点∞.i i z i z z f z z f s z z --=-+=-+=-=→→1112lim )()1(lim ],[Re 3111i i z i z z f z z f s z z +=+=-+=-=→→8181lim )()2(lim ],[Re 32227)2311(lim 21]0,)21)(1(1[Re ]0,1)1([Re ],[Re ''230332-=+-+-=--+-=-=∞→z z iz z z z iz s zz f s f s z五．1.证明: 当C 为任何不通过原点的闭曲线时，⎰=Cdz z012；（3分）. 2. 沿怎样的简单闭曲线有⎰=++Cdz z z 0112；（3分）.3. 计算⎰--Cdz z z )3)(1(15，2|:|=z C .（3分）； 1. 证明：当C 不包含0=z 时，由柯西定理得，⎰=Cdz z 012； 当C 包含0=z 时，由高阶导数的柯西积分公式得，0)1(!121'2==⎰Ci dz z π 2. 当i z 23212,1±-=均不被简单曲线C 包围或全部被包围时，⎰=++Cdz z z 0112. 3.]]),[Re ]3,[([Re 2)3)(1(15∞+-=--⎰f s f s i dz z z Cπ121)02421(2])0,)31)(11(1[Re 2421(252ii z z z s i πππ-=+-=----=六．计算⎰Cdz z __，这里曲线C 为)11(12≤≤--+=x x i x z ，方向分别取逆时针和顺时针方向 （6分）.解：⎪⎩⎪⎨⎧-==⎰⎰-，顺时针逆时针i ,__ππθθθi d e ie dz z C i i C七．将函数)(1)(i z z z f -=分别在圆环1||0<<z 与+∞<-<||1i z 内展成罗朗级数（8分）.解：（1）当1||0<<z 时，++++++=+++++=--•=-=--112221])()(1[)1(11)(1)(n n n iz i z i z z i i zi z i z zi iz i zi z z z f（2）当+∞<-<||0i z 时，+--+--+---=+--+--+---=-+•-=+-•-=•-=-=+24232222)()1()()()(1])()1()(1[)(111)(1)(1)(11)(1)(1)(n n nn ni z i i z i i z i i z i z i i z i i z i i z iz i i z i i z i z z i z i z z z f+--+--+--=-++--+--+--=-+nn nn i z i i z i i z i iz i iz i i z i i z i iz i )()1()(1)11()()1()(1112'2八．计算dz z z z ⎰=+2||651 （8分）. 解：原式=∑=+6165],1[Re 2k k z z z s i π iz z s i z z z s i z z s i ππππ2]0,)1(1[Re 2]0,1111[Re 2],1[Re 2626565=+=•+=∞+-= 九．计算θθθπd ⎰+202cos 45sin （8分）.解：设θi e z =，则izdzd =θ，iz z 21sin 2-=θ，z z 21cos 2+=θ原式dz z z z z i z ⎰=++-=1||2222)4104()1(2 dz z z z z i z ⎰=++-=1||2222)4104()1(2 在1||<z 内，有一个二阶极点01=z 和一个一阶极点512-=z ， 85]0),([Re -=z f s83]51),([Re =-z f s所以，原式4]}51,[Re ]0,[{Re 22ππ=-+=f s f s i i十．讨论将半径为1，圆心分别在0=z 和1=z 处的两圆的公共部分在分式线性映照)2321()2321(i z i z --+-=ω下的图形 （8分）. 解：两圆1||=z 和1|1|=-z 的交点为i z 23212,1±=，两圆在2,1z 的夹角分别为32π， 该分式线性映照将1z 映成原点，而把2z 映成∞，且0|1'≠z ω，因此，分式线性映照在1z 是共形映照，所给的区域经映照后映照成以原点为顶点的角形区域，张角等于32π. 另外，为了确定角形域的位置，取1|21-==z ω，所以，所得的角形域如右图所示：十一. 求函数0,)(||>=-ββt e t f 的傅氏变换 （6分）.解：dt e e F t i t ⎰+∞∞---=ωβω||)(22)(0)(211ωββωβωβωβωβ+=++-=+=⎰⎰+∞+-∞--i i dte dt et i ti十二.用拉普拉斯变换和它的逆变换求下列一阶常系数非齐次常微分方程的解： 0)0(,2'=+=-y t e y y t （6分）.解：作Laplace 变换，记Y(s)=L[y(t)], 则 2121)()(ss s Y s sY +-=- 1)(112111111121)1(1)2)(1(1)(2222--=---=---+---=-+--=t e t y ss s s s s s s s s s s s Y t。

北 京 交 通 大 学2007-2008-2-《复变函数与积分变换A 》期末考试试卷(B)参考答案一．填空题（本题满分14分，每空1分），请将合适的答案填在空中.1．复数i i i z +-=2184，则=)Re(z _______；=)Im(z _______；=||z _______ =)arg(z ________________，复数z 的三角表达式为_____________________ 指数表达式为_______________________________________________________ 解：因为i i i i i i z 31414218-=+-=+-=所以，1)Re(=z ；3)Im(-=z ；10||=z ；3arctan )arg(-=z ， 复数z 的三角表达式为)]sin(arg )[cos(arg 10z i z +， 指数表达式为)arg(10z i e.2．方程083=+z 的所有根是2,1,0,28323==-=+k ez k iππ3．.,2,1,0,)1()]24(2[ln )1( ±±===++++k ee i k i i i iLn i ππ4．函数z ln 在复平面上的连续性为在除去原点和负实轴的平面上连续. 5．若幂级数∑∞=+1)(n nn i z c 在i z =处发散，则该级数在1=z 的敛敛性为发散6．映射ze w =将带形域43)Im(0π<<z 映照成角形域43)arg(0π<<z . 7．幂函数3z w =，把扇形域2||,3)arg(0<<<z z π映照为w 平面上的扇形域8||,)arg(0<<<z z π.8．在傅氏变换意义下，函数)(1t f 和)(2t f 的卷积)(*)(21t f t f 定义⎰+∞∞--τττd t ff )()(21.9．设)()(0t t t f -=δ，则)]([t f F =0t i eω-.二．判断下列命题的真假（本题满分10分，共有10道小题，每道小题1分），对的填“∨”，错的填“⨯”.（∨）1．指数函数z e 是以i π2为周期的周期函数. （⨯）2．正弦函数z sin 一定是有界函数. （⨯）3．奇点一定是孤立奇点.（⨯）4．)(z f 在0z 可导是)(z f 在0z 解析的充分条件.（∨）5．若u 和v 都是D 内的调和函数，且满足柯西-黎曼方程，则 iv u z f +=)(在区域D 内是解析函数.（⨯）6．若积分⎰=Cdz z f 0)(，C 是一条简单闭曲线，则)(z f 在C 内无奇点.（⨯）7．幂级数∑∞=1n nnz 的收敛半径为1，则在1||=z 上的点一定处处收敛.（⨯）8．函数y x v +=是y x u +=的共轭调和函数.（⨯）9．如果无穷远点∞是)(z f 的一阶极点，则0=z 是)1(zf 的一阶极点，并且)1(lim ]),([Re 0zzf z f s z →=∞.（⨯）10．映射2z w =在z 平面上每一点都具有伸缩率和旋转角的不变性.三．讨论函数33)1()(y i x z f -+=的可导性、解析性（8分）.解：设3x u =，3)1(y v -=，则v u ,处处可微且22)1(3,0,0,3y yvx v yux x u --=∂∂=∂∂=∂∂=∂∂但1,00)1()1(332222==⇒=-+⇒--=⇒∂∂=∂∂y x y x y x yv x u 即仅在点)1,0(处满足柯西-黎曼方程，因此，33)1()(y i x z f -+=在点)1,0(处可导，但在整个复平面上不解析.四．在扩充复平面上找出函数23)(23+-+=z z iz z f 的孤立奇点并加以分类，若是极点，指出其阶（或级）数，最后分别计算在每个孤立奇点的留数（8分）.解：)2)(1(23)(323--+=+-+=z z iz z z i z z f所以，)(z f 共有两个一阶极点2,121==z z 和一个无穷远点∞.i i z i z z f z z f s z z --=-+=-+=-=→→1112lim )()1(lim ],[Re 3111i i z i z z f z z f s z z +=+=-+=-=→→8181lim )()2(lim ],[Re 32227)2311(lim 21]0,)21)(1(1[Re ]0,1)1([Re ],[Re ''230332-=+-+-=--+-=-=∞→z z iz z z z iz s zz f s f s z五．1.证明: 当C 为任何不通过原点的闭曲线时，⎰=Cdz z012；（3分）. 2. 沿怎样的简单闭曲线有⎰=++Cdz z z 0112；（3分）.3. 计算⎰--Cdz z z )3)(1(15，2|:|=z C .（3分）； 1. 证明：当C 不包含0=z 时，由柯西定理得，⎰=Cdz z 012； 当C 包含0=z 时，由高阶导数的柯西积分公式得，0)1(!121'2==⎰Ci dz z π 2. 当i z 23212,1±-=均不被简单曲线C 包围或全部被包围时，⎰=++Cdz z z 0112. 3.]]),[Re ]3,[([Re 2)3)(1(15∞+-=--⎰f s f s i dz z z Cπ121)02421(2])0,)31)(11(1[Re 2421(252ii z z z s i πππ-=+-=----=六．计算⎰Cdz z __，这里曲线C 为)11(12≤≤--+=x x i x z ，方向分别取逆时针和顺时针方向 （6分）.解：⎪⎩⎪⎨⎧-==⎰⎰-，顺时针逆时针i ,__ππθθθi d e ie dz z C i i C七．将函数)(1)(i z z z f -=分别在圆环1||0<<z 与+∞<-<||1i z 内展成罗朗级数（8分）.解：（1）当1||0<<z 时，++++++=+++++=--∙=-=--112221])()(1[)1(11)(1)(n n n iz i z i z z i i zi z i z zi iz i zi z z z f（2）当+∞<-<||0i z 时，+--+--+---=+--+--+---=-+∙-=+-∙-=∙-=-=+24232222)()1()()()(1])()1()(1[)(111)(1)(1)(11)(1)(1)(n n nn ni z i i z i i z i i z i z i i z i i z i i z iz i i z i i z i z z i z i z z z f+--+--+--=-++--+--+--=-+nn nn iz i i z i i z i i z i iz i i z i i z i iz i )()1()(1)11()()1()(1112'2八．计算dz z z z ⎰=+2||651 （8分）. 解：原式=∑=+6165],1[Re 2k k z z z s i π iz z s i z z z s i z z s i ππππ2]0,)1(1[Re 2]0,1111[Re 2],1[Re 2626565=+=∙+=∞+-= 九．计算θθθπd ⎰+202cos 45sin （8分）. 解：设θi e z =，则izdzd =θ，iz z 21sin 2-=θ，z z 21cos 2+=θ原式dz z z z z i z ⎰=++-=1||2222)4104()1(2 dz z z z z i z ⎰=++-=1||2222)4104()1(2 在1||<z 内，有一个二阶极点01=z 和一个一阶极点512-=z ， 85]0),([Re -=z f s83]51),([Re =-z f s所以，原式4]}51,[Re ]0,[{Re 22ππ=-+=f s f s i i十．讨论将半径为1，圆心分别在0=z 和1=z 处的两圆的公共部分在分式线性映照)2321()2321(i z i z --+-=ω下的图形 （8分）. 解：两圆1||=z 和1|1|=-z 的交点为i z 23212,1±=，两圆在2,1z 的夹角分别为32π， 该分式线性映照将1z 映成原点，而把2z 映成∞，且0|1'≠z ω，因此，分式线性映照在1z 是共形映照，所给的区域经映照后映照成以原点为顶点的角形区域，张角等于32π. 另外，为了确定角形域的位置，取1|21-==z ω，所以，所得的角形域如右图所示：十一. 求函数0,)(||>=-ββt e t f 的傅氏变换 （6分）.解：dt e e F t i t ⎰+∞∞---=ωβω||)(22)(0)(211ωββωβωβωβωβ+=++-=+=⎰⎰+∞+-∞--i i dte dt e t i ti十二.用拉普拉斯变换和它的逆变换求下列一阶常系数非齐次常微分方程的解： 0)0(,2'=+=-y t e y y t （6分）.解：作Laplace 变换，记Y(s)=L[y(t)], 则 2121)()(ss s Y s sY +-=- 1)(112111111121)1(1)2)(1(1)(2222--=---=---+---=-+--=t e t y ss s s s s s s s s s s s Y t。

2005级VB期末试题部分（2006 2007 — 2008 学年第二学期《复变函数》课程考试试卷A注意：1、本试卷共 3 页；2、考试时间120分钟3、姓名、学号必须写在指定地方阅卷负责人签名：一、填空题（本题共5小题，每小题3分，满分15分.）1．Ln i＝2．＝3．若函数2222()(2)f z x axy y i x xy y=+-+-++在复平面内处处解析，则a= ____4．幂级数(1)n nni z∞=+∑的收敛半径为______5．复变函数积分212(1)zdzz-=-⎰＝二、选择题（本题共6小题，每小题3分，满分18分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.）1．点0z=为函数2sin zz的[ ]（A）可去奇点（B）本性奇点（C）一级极点（D）二级极点2．下列命题正确的是[ ](A) 如果()f z在z连续，那么()f z'存在；(B) 如果()f z'存在，那么()f z在z解析；.(C) 如果z是()f z的奇点，那么()f z在z不可导；(D) 如果()f z在区域D内解析且实部为常数，那么()f z在D内是常数.3．关于函数()f z z=的性质下列说法错误的是[ ]（A）()f z在整个复平面上都是连续的（B）()f z仅仅在原点可导（C）()f z在原点解析（D）()f z在整个复平面上都不解析4．下列说法正确的是[ ](A) 每一个幂级数在它的收敛圆周上处处收敛；(B) 每一个幂级数的和函数在收敛圆内解析；(C) 幂级数(2)nnnc z∞=-∑在0z=收敛且在3z=发散；(D) 在z连续的函数一定可以在z的邻域内展开成泰勒级数.三峡大学试卷纸教学班号序号学号姓名命题教审题教…………………….………….……试题不要超过密封线………….………………………………2005级VB 期末试题部分（20065． 设221()z f z d z ζζζ=+=-⎰， 则(3)f ＝[ ]（A ）0 （B ）2i π （C ）14i π （D ）6i π6． 级数0n n i n∞=∑是[ ](A ) 绝对收敛 (B ) 条件收敛 (C ) 发散 (D ) 无法判断三、试解下列各题（本题满分67分.）1．（本小题20分）计算下列积分:(1) 3()z C e dz z α-⎰ 其中1α≠， C 为正向圆周：1z =(2)2211Cz z dz z -+-⎰， 其中 C 为正向圆周：2=z(3) 22(1)zz e dz z z =-⎰ ，(4) 10sin z zdz ⎰2．（本小题12分）证明：32(,)3u x y y x y =-为调和函数，并求其共轭调和函数),(y x v 和由它们组成的解析函数)(z f ，使0)0(=f .三峡大学 试卷纸 教学班号 序号 学号 姓名命题教师 审题教…………………….………….……试 题 不 要 超 过 密 封2005级VB 期末试题部分（20063．（本小题8分）将函数)2)(1(1--z z 在021z <-<内展成Laurent 级数.4．（本小题15分）计算下列函数在有限奇点处的留数： （1） 212z z z+-（2）241ze z- （3） tan z π5．（本小题12分）判定下列函数在何处可导，在何处解析？（1） w z = （2） 2()f z x iy =- （3）()(cos sin )x f z e y i y =+三峡大学 试卷纸 教学班号 序号 学号 姓名命题教师 审题教…………………….………….……试 题 不 要 超 过 密 封2007 — 2008 学年第 二 学期 《复变函数》课程考试试卷A 参考答案一、填空题 (每小题3分)1．(2)()2k i k Z ππ+∈ 2．cos(2sin(2()k i k k Z ππ+∈3．2a = 4．25．0 二、选择题(每小题3分)1．C 2．D 3．B 4．B 5．A 6．B三、试解下列各题1．（本小题20分）计算下列积分:(1) 3()zC e dz z α-⎰ 其中1α≠， C 为正向圆周：1z = 解: 当1α>时，由Cauchy 积分定理得，原式＝0 …………2分 当1α<时，由Cauchy 积分公式得， 原式＝2()2!zz i e e i ααππ=''=…………5分 (2)2211Cz z dz z -+-⎰， 其中 C 为正向圆周：2=z解: 方法一: 由Cauchy 积分公式得，原式＝122(21)4z i z z i ππ==-+ ………………………………5分 方法二:22(21)1211C C z dz z z z dz z ⎡⎤++⎢⎥-⎣⎦-+=-⎰⎰0442(21)1C C dz i i z dz z ππ+=+==+-⎰⎰ (3) 22(1)zz e dz z z =-⎰ ， 解: 分别作两个互不相交互不包含的正向小圆周12,C C ,使1C 只包含奇点0,2C 只包含奇点1, 则122222(1)(1)(1)z z zC C z e e z ze dz dz dz zz z z =-=+--⎰⎰⎰012222(1)zzz z e e ii i z zπππ=='⎛⎫=+=⎪-⎝⎭…………5分 (4)10zsin zdz ⎰解: 函数zsin z 在复平面内解析, 积分与路径无关, 故101(cos sin )cos1sin1sin z z z z zdz =-+=-+⎰ (5)分2．（本小题12分）证明：32(,)3u x y y x y =-为调和函数，并求其共轭调和函数),(y x v 和由它们组成的解析函数)(z f ，使0)0(=f .解：（1）因为 y x u xy xu6622-=∂∂-=∂∂ y yux y yu 6332222=∂∂-=∂∂ 所以 02222=∂∂+∂∂yux u ，即),(y x u 是调和函数。