M序列发生器

m序列发生器的作用
m序列发生器是一种能够产生伪随机序列的电子设备或算法。

它的主要作用有：
1. 加密通信：m序列发生器可以用于生成加密密钥序列，用于对通信数据进行加密，保护通信内容的安全性。

2. 伪随机数生成：m序列发生器可以用于生成伪随机数序列，可以应用在密码学中的伪随机数生成算法、模拟实验、随机化算法等应用中。

3. 信号处理：m序列发生器可以用于产生具有特定性质的信号序列，如具有较好频谱特性的序列、跳频信号序列等，广泛应用于通信领域、雷达系统、无线电测量等各种信号处理应用中。

4. 探测器测试：m序列发生器可以用于对数字通信中的接收机进行性能测试，通过与已知正常输入进行比较，可以检测接收机的误码率、误比特率、误帧率等性能指标。

总之，m序列发生器的作用主要体现在加密通讯、伪随机数生成、信号处理和探测器测试等方面。

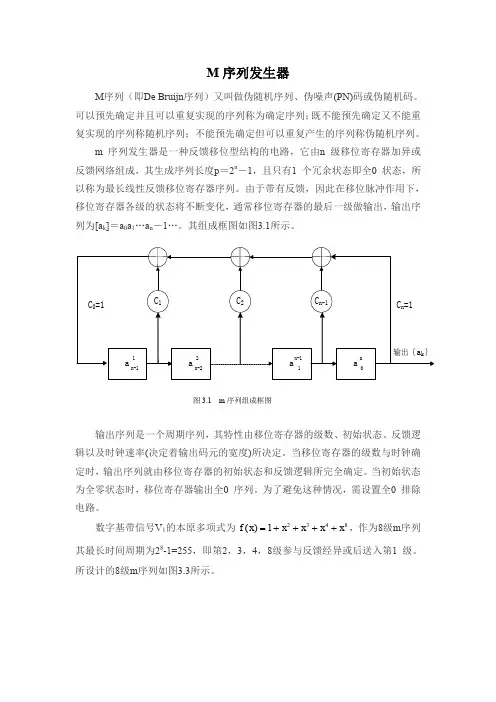
M 序列发生器M 序列（即De Bruijn 序列）又叫做伪随机序列、伪噪声(PN)码或伪随机码。

可以预先确定并且可以重复实现的序列称为确定序列；既不能预先确定又不能重复实现的序列称随机序列；不能预先确定但可以重复产生的序列称伪随机序列。

m 序列发生器是一种反馈移位型结构的电路，它由n 级移位寄存器加异或反馈网络组成，其生成序列长度p ＝2n －1，且只有1 个冗余状态即全0 状态，所以称为最长线性反馈移位寄存器序列。

由于带有反馈，因此在移位脉冲作用下，移位寄存器各级的状态将不断变化，通常移位寄存器的最后一级做输出，输出序列为[a k ]＝a 0a 1…a n －1…。

其组成框图如图3.1所示。

输出序列是一个周期序列，其特性由移位寄存器的级数、初始状态、反馈逻辑以及时钟速率(决定着输出码元的宽度)所决定。

当移位寄存器的级数与时钟确定时，输出序列就由移位寄存器的初始状态和反馈逻辑所完全确定。

当初始状态为全零状态时，移位寄存器输出全0 序列。

为了避免这种情况，需设置全0 排除电路。

数字基带信号V 1的本原多项式为84321)(x x x x x f ++++=，作为8级m 序列其最长时间周期为28-1=255，即第2，3，4，8级参与反馈经异或后送入第1 级。

所设计的8级m 序列如图3.3所示。

图3.1 m 序列组成框图a n-11a n-22a 1n-1a 0n C 1C 2C n-1C n =1C 0=1输出｛a k ｝依据上图原理，设计了一种通过手动置数产生M 序列的电路，其电路设计如图3.4所示，该图由Protel SE99绘制，再根据该图搭建硬件电路，图中的单刀开关可以用拨码开关代替。

电路分析：全0状态时，采用此方法设计的m 序列发生器不具有自启动特性。

为了使电路启动，可以断开开关S 1，将74LS194 的工作方式控制端S 1置高电平，这时S 1和S 0均为高电平，即S 1S 0＝11，74LS194 处于置数状态，把输入端的初始状态10000000 置到输出端。

１ 、引言
ＶＨＤＬ（超高速硬件描述语言）是一种 符合 Ｉ Ｅ Ｅ Ｅ 工业标准的硬件描述语言，在 ＥＤＡ（电子设计自动化）领域得到广泛的 应用。应用 ＶＨＤＬ 进行电子系统设计，可 以使用自顶向下的设计方法，设计成果标 准化，可移植性好，具有与硬件无关的特 性，因此特别适合于大规模的专用电子系 统的开发。
３．２ 一般情况 为了得到纳米摩擦在一般情况下的规 律性，模拟过程中设置了相关可调参数，如 表 １ 所示。 在 ＫＢＴ＝０．１ ε，势能 ｕ０（０．０１ ε～０．０４ ε），ＵＰ（０．０３～０．０９），ＵＡ（０．０３～０．０９）情况 下，模拟 Ｃ 在（０．０３～０．０９）之间对摩擦系数 的影响。图 ３ 给出了不同势能 ｕ０ 大小，不 同 ＵＰ，ＵＡ 情况下得到的摩擦系数的倒数 随 Ｃ 的变化曲线。 由图可以看出，最显著的特点是在不 同摩擦条件下的摩擦系数倒数曲线随 Ｃ 的 变化在 Ｃ＝０．５ 处出现了汇聚且出现最小值， 而在两侧则离散增加。当 Ｃ＝０．５ 时出现摩 擦系数倒数最小值，也就是出现了摩擦系 数最大值，即在完全匹配的情况下出现摩 擦最大值。完全匹配处之所以出现摩擦最 大值的原因在于此时所有的附加原子步伐 统一，能够同时受到衬底原子的拉力而加 速移动，又能够同时受到阻力减速，相互之 间无法将能量转化为势能保存，而只能以 热量的形式进行耗散。曲线的聚合同时说 明对于纳米摩擦无论势能形式如何组合变 化，势能大小的如何变化，在对摩擦的调制 作用中界面晶格匹配度 Ｃ 对整个摩擦过程 的调制作用最为明显，在完全匹配的情况 下摩擦最大。 由图可以发现另一个特点，摩擦系数 在 Ｃ 为 ０．５ 两侧随Ｃ的增大或者减少而迅速 减小，但在 Ｃ 为 ０．８ 时出现了转折点。此转 折点在不同的条件下，对摩擦的调制作用 表现出不同程度的影响，说明此转折点为 复合势能情况下产生的影响，而这种调节 作用与势能周期比例 Ｕ Ｐ 和势能振幅比例 ＵＡ 之间存在非线性关系。转折点的出现原 因为附加原子在不同的衬底复合势能阱中 进行运动时受到衬底原子的拉扯作用产生 了强烈的声子振动所带来的影响，这种拉 扯作用主要受到势能振幅比例与势能周期 之间的比例关系的影响。当处于衬底势能 最高点时，附加原子将出现失稳并自动跳跃 到下一势能最低点，然后在此平衡位置剧烈 震荡和激发声子，从而使能量不可逆地以声

m序列基本概念：M序列（即De Bruijn序列）又叫做伪随机序列、伪噪声(PN)码或伪随机码。

可以预先确定并且可以重复实现的序列称为确定序列；既不能预先确定又不能重复实现的序列称随机序列；不能预先确定但可以重复产生的序列称伪随机序列。

具体解释于一个n级反馈移位寄存器来说，最多可以有2^n 个状态，对于一个线性反馈移位寄存器来说，全“0”状态不会转入其他状态，所以线性移位寄存器的序列的最长周期为2^n-1。

当n级线性移位寄存器产生的序列{ai}的周期为T= 2^n-1时，称{ai}为n级m序列。

当反馈函数f（a1,a2,a3,…an）为非线性函数时，便构成非线性移位寄存器，其输出序列为非线性序列。

输出序列的周期最大可达2^n ，并称周期达到最大值的非线性移位寄存器序列为1.m序列的产生原理和结构m序列是n 级二进制线性反馈移位寄存器除去输出为0的状态外，产生的周期为2 n -1 的最大可能长度序列，又称为最大长度线性反馈移位序列。

其产生的原理如图1所示。

PN序列发生器由n级移位寄存器，模二加法器和反馈线三个部分组成。

图中，c i ( i =1…n ) 为反馈系数，若c i =1,表示有连接，有反馈，若c i =0则表示断开，无反馈。

c i 的取值决定了移位寄存器的反馈连接和序列的结构，故是一个很重要的参量。

2.m序列的基本性质(1) 移位相加特性。

一个m序列与其任意次延迟移位后产生的另一个不同序列模2相加，得到的仍是该m 序列的延迟移位序列。

如，0100111向右移1次产生另一个序列1010011 ，模2相加后的序列为1110100 ，相当于原序列右移3次后得到的序列。

(2) 平衡特性。

在m序列的每个2n－1周期中，"1"码元出现的数目为次，"0"码元出现的数目为2n －1－1 次，即"0"的个数总是比"1"的个数少一个，这表明，序列平均值很小。

M序列发生器设计实验一、实验原理：M序列码也称伪随机序列码，其主要特点是：（1）每个周期中，“1”码出现2n-1次，“0”码出现2n-1次，即0、1出现概率几乎相等。

（2）序列中连1的数目是n，连0的数目是n-1。

（3）分布无规律，具有与白噪声相似的伪随机特性。

由于具有这些特点，m序列码在通信、雷达、系统可靠性测试等方面获得了广泛地应用。

m序列码发生器是一种反馈移位型结构的电路，它由n位移位寄存器加异或反馈网络组成，其序列长度M＝2n-1，只有一个多余状态即全0状态，所以称为最大线性序列码发生器。

由于其结构已定型，且反馈函数和连接形式都有一定的规律，因此利用查表的方式就设计出m 序列码。

列出部分m序列码的反馈函数F和移存器位数n的对应关系。

如果给定一个序列信号长度M，则根据M＝2n-1求出n，由n查表便可以得到相应的反馈函数F。

二、基于DSP Builder 的设计M 序列发生器可由线性反馈寄存器（Linear Feedback Shift Registers,LFSR ）来产生，如图1所示。

图1 线性反馈移位寄存器的构成其特征多项式可表示为:∑==ni i i x C x F 1)(在图1中涉及的乘法和加法都是指模二运算的乘法和加法，即逻辑与和逻辑或。

要产生最长的线性反馈移位寄存器序列的n 级移位寄存器，其特征多项式必须是n 次本原多项式。

例如n=5，可以生成M 序列的5级LFSR 的特征多项式，即：125++x x ，此式可生成的M 序列的周期为：125-。

下面以M 序列发生器模型125++x x 为例，利用DSP Builder 构建一个伪随机序列发生器。

图2显示了上式的DSP Builder 模型表述，这里采用相连的延时单元级作为移位寄存器，用异或（XOR ）完成模二加运算，输出为Output 。

图2 M 序列发生器模型但应注意，图2所示的电路一般无法正常工作。

这是由于在DSP Builder 默认的延时单元在开始工作时，存储内容为0，而对于M 序列来说，起始序列为全0，那么根据多项式，输出序列也将为0.全0序列不是正常的M 序列。

一
ＥＣＭ（２）在ｃＰ（２）开始之前被足够优先地传到以确保ＳＴＢ 能够在ＣＰ（２）开始之前得到Ｃｗ（２）。
ＣＡ系统Ｂ通过产生一条包含２个ＣＷ信息的ＥＣＭ来 达到同样的效果。在如时刻，ＥＣＭＧｅｎ Ｂ收到ＣＷ（２），在￡ｚ 时刻，他就可以生成ＥＣＭ（１）。ＥＣＭ（１）内包含ＣＷ（１）和 ＣＷ（２），他在ＣＰ（１）的中间即ｔ。时刻被传输。这就确保了 ＳＴＢ在ＣＰ（２）开始前得到ＣＷ（２）。当ＣＰ（２）开时后，即如时 刻，传输的ＥＣＭ（２）中包含了ＣＷ（２）和ＣＷ（３）信息。
收稿日期ｔ ２００４一０３—０３
列的初相位。 智能控制器通过外三总线对该器件中的这６个字节
初始化，电路即可输出所需周期、初相位的ｍ序列。
图ｌ可编程ｍ序列的逻辑电路结构
２多周期ｍ序列生成单元的电路设计
ｍ序列发生器一般由线性反馈移位寄存器组成，他的 反馈多项式为本原多项式。实现移位寄存器的长与反馈式 的编程选择，即可实现对ｍ序列的控制。如图２所示电路， 该电路可以实现序列周期户一２２—１～２‘一１的变化输出。 其中ｅｎ是周期控制字ｏｏｈ单元经译码后的输出值；ＬＲＮ 与ｐｍ完成序列的初相位控制。ＰＲＮ由ｏｌｈ～０５ｈ存储单 元的３２ ｂ数据给定。ｄ—ｉｎ为用户串行数据输入端。正常使 用时，首先ＣＬＲＮ＝０，图２中所有的Ｄ触发器为零状态， 然后在ＣＬＲＮ与ＰＲＮ联合作用下，置序列的初相位；最后 由ｅｎ控制序列的周期。于是，就可以实现ｍ序列的周期、 初相位的控制。显然，按照图２所示的电路结构，可以将 其扩展到３２级线性移位寄存器电路，相应的ｅｎ，ｐｒｎ也跟 随增加，即可实现我们最初的设计思想。ｄ—ｏｆｆ（ｊ）为特征 反馈。
ｐｒｏｇｒａｍｍａｂｌｅ ｏｎ ｐｅｒｉｏｄｓ ｆｒｏｍ ２２—１ ｔｏ ２３２—１．Ｗｅ ｅｘｐｌｉｃａｔｅｄ ｍａｋｉｎｇ ｐｒｉｎｃｉｐｌｅ ａｎｄ ｗｏｒｋｉｎｇ ｃｏｕｒｓｅ，ｆｕｒｔｈｅｒｍｏｒｅ，ｇａｖｅ ｔｈｅ ｈａｒｄｗｉｒｅ

一．伪随机序列1．研究背景2．发展历史3.应用及其意义二．m 序列1． 概念由线性反馈移位寄存器产生的周期最长的序列。

它是由带线性反馈的移存器产生的周期最长的一种序列,是多级移位寄存器或其他延迟元件通过线性反馈产生的最长的码序列。

2． 产生原理一般来说,在一个n 级的二进制移位寄存器发生器中，所能产生的最大长度的码序周期为12-n 。

以m=4为例,若其初始状态为),0,0,0,1(),,,(0123=a a a a ,则在移位一次时,由3a 和0a 模2相加产生新的输入,1014=⊕=a 新的状态变为),0,0,1,1(),,,(0123=a a a a 这样移位15次后又回到初始状态,但若初始状态为(0,0,0,0),则移位后得到地全是0状态,这说意味着在这种反馈中要避免出现全0的状态.在4级移存器共有1624=种不同状态,除全0状态以外还有15种可用.即由任何4级反馈移存器产生的序列的周期最长为15,满足12-n (当n为4时).图1:m 序列的产生举例：4级m 序列产生器及其状态图2中，ai (i = 0 – n ) － 移存器状态。

ai = 0或1。

ci －反馈状态。

ci = 0表示反馈线断开，ci = 1表示反馈线连通。

如图2中示出的一个一般的纯属反馈移存器的组成,反馈线的连接状态用1c ,=i i c 表示表示此线接通(参加反馈),0=i c 表示断开,反馈线的接线状态不同,就可能以改变此移存器序列的周期.为了产生m 序列, 必须确定其特征多项式, 以此确定线性反馈移位寄存器的反馈结构, n 级线性反馈移位寄存器的特征方程定义为：其中c i ( i= 1, 2, ⋯⋯, n) 根据m 序列周期的不同, 取值为0 或1。

此特征多项式又称本原多项式, n ≤20 的本原多项式如表1 所示:此外, 本原多项式f ( x ) 的反多项式也是本原多项式, 反多项式的定义为:因为ci( i= 1, 2, ⋯⋯, n) 只取0或1值, 故上式可写成:其中d i( i= 1, 2, ⋯⋯, n) 也取0 或1 值, 因此按这两种本原多式构成的线性反馈移位器都可以产生m 序列。

基于FPGA的ｍ序列发生器摘要ｍ序列广泛应用于密码学、通信、雷达、导航等多个领域，本文提出了一种基于FPGA的伪随机序列产生方法，应用移位寄存器理论从序列的本原多项式出发，获得产生该序列的移位寄存器反馈逻辑式，结合FPGA芯片结构特点，在序列算法实现中采用元件例化语句。

算法运用VHDL语言编程，以A1tera的QuartusⅡ软件为开发平台，给出了序列的仿真波形。

序列的统计特性分析表明：该方法产生的序列符合ｍ序列的伪随机特性，验证了算法的正确性。

关键词：ｍ序列；移位寄存器理论；VHDL语言1 m序列m序列是伪随机序列的一种 ,结构简单 ,实现方便。

在现代工程实践中 , m 序列在通讯、导航、雷达、通信系统性能的测量等领域中有着广泛的应用。

例如 , 在连续波雷达中可用作测距信号 , 在遥控系统中可用作遥控信号 , 在多址通信中可用作地址信号 , 在数字通信中可用作群同步信号 ,还可用作噪声源及在保密通信中起加密作用等。

伪噪声发生器在测距、通信等领域的应用日益受到人们重视。

目前，m序列产生实现方法主要有3种：(1)门电路实现该方法设计简单，但随移位寄存器级数的增长，电路装调困难，且占用的印制板面积较大。

(2)DSP编程实现该方法专业性过强，不适合一般用户。

(3)VHDL与CPLD实现由于CPLD的高集成度，而且VHDL语言编程较为方便，故可以大大减少电路的装调的困难。

文章提出VHDL语言实现，，l序列电路是周期、初相位可编程变化的，其应用较为灵活，通过微处理器对其进行适当的初始化，即可产生用户所需周期、初相位的m序列输出。

用软件方式构成的特点是采用灵活的数据查询方式可以获得任意级数 n 的本原多项式系数 ,从而实现 m 序列的产生 , 但速度受到单片机工作速度的限制。

而 FPGA 具有硬件电路实现的优点 , 又具有设计上的灵活性 , 并且由于FPGA 便于实现大规模的数字系统。

1.1 理论基础m 序列是最长线性反馈移位寄存器序列的简称，它是由带线性反馈的移位寄存器产生的周期最长的一种序列。

王会华， 李宝平 （南京邮电大学 无线通信与电磁兼容实验室， 江苏， 南京， ２１ ０００３ ）
摘 要：伪随机码越来越受到人们的重视， 被广泛应用于导弹、卫星、飞船轨道测量和跟踪、雷达、导航、移
动通信、保密通信和通信系统性能的测量以及数字信息处理 系 统 中。ｍ 序 列 是 伪随 机 码 中， 带 线 性 反馈
图 １ 线性反馈移位寄存器
ｎ
$ ａｎ＝ｃ１ａｎ－ １ #ｃ２ａｎ－ ２ #…#ｃｎ－ １ ａ１#ｃｎａ０＝ ｃｉａｎ－ ｉ
（１）
ｉ＝１
ｃｉ的取值决定了移位寄存器的反馈连接和序列的结 构 ，
故 ｃｉ是一个很重要的参量。用特征方程表示为：
ｎ
$ ｆ
! ｘ " ＝ｃ０＋ｃ１ｘ＋ｃ２ｘ２＋…
ｎ
＋ｃｎｘ ＝
ｉ
ｃｉｘ
信号， 实现 １ｍｓ 清 零 一 次。系 统 清 零后 ， Ｄ 触发器输出状态均为低电平， 为避免 ｍ 序 列 发 器 输 出 “全 ０”信 号 ， 可 在 “模 二 加 ”运 算 后 加一 个 “非 门 ”。ＣＬＫ 端 为 输 入 时 钟 ， 产生的是 ２．０４８ＭＨｚ 时钟信号。 ２．２ 软件实现 软件实现的方法更多。用软件实现的方法具有更好的 可移植性， 更改也更容易。可通过 Ｃ 语言程序编程来产生 ｍ 序列， 其特点是通过查询本原多项式链表， 得到任意级数 ｎ 的本原多项式系数， 级数 ｎ 的调整简单容易， 产生伪码的外 围硬件电路也无须改变。也可通过 Ｃ＋＋来实现， 特点是函数 清晰， 算法简单， 实现流程和程序相对比较简单。下面介绍 三种软件仿真方法实现 ｍ 序列。 ２．２．１ ＭＡＴＬＡＢ 仿真［５］ ＭＡＴＬＡＢ 除了原有的数 值 计算 功 能 之外 ， 还 具 备了 越 来越多的其他功能， 其 Ｓｉｍｕｌｉｎｋ 是比 较 突 出的 一 种 动态 仿 真功能， 是实现动态系统建模 、仿 真的 一 个 集成 环 境 。近几 年 ， 在 学术 界 和 工 业 领 域 ， Ｓｉｍｕｌｉｎｋ 已 经 成 为 在 动 态 系 统 建 模和仿真方面应用最广泛的软件包之一。 图 ４ 中用到的模块分别为 Ｄ 触发器， 时钟源， 单位延时

平衡Gold序列的产生与搜索方法
平衡Gold序列是一类具有优良伪随机性和自相关性的二元序列。产生平衡 Gold序列的方法主要有两种：一是通过平衡Gold多项式产生平衡Gold序列； 二是通过选择适当的m序列和反馈函数产生平衡Gold序列。搜索方法主要有基 于差分编码的搜索算法和基于自相关函数的搜索算法。
3、信息隐藏：平衡Gold序列可以用于信息隐藏中的隐写术，以隐藏敏感信息 在公开信息中。由于平衡Gold序列具有优良的自相关性，它可以用于构造高效 的隐写算法，提高信息隐藏的安全性和鲁棒性。
未来展望
随着技术的发展，平衡Gold序列的研究将面临新的挑战和机遇。以下是一些未 来可能的研究方向：
1、高效产生方法：目前平衡Gold序列的产生方法还比较耗时，因此研究更高 效的产生方法以提高搜索速度和降低计算成本是未来的一个研究方向。
1、反馈函数设计：反馈函数是m序列发生器的核心部分，其设计的好坏直接影 响到m序列的性能。一个好的反馈函数应该具有较低的误码率、较高的线性复 杂度、易于实现等优点。常用的反馈函数包括异或、同或、与等运算。
2、LFSR级数和反馈位数选择：m序列发生器的性能与LFSR的级数和反馈位数 密切相关。一般来说，增加LFSR的级数和反馈位数可以提高m序列的性能，但 同时也会增加硬件实现的复杂度和功耗。因此，在设计中需要根据实际需求选 择合适的LFSR级数和反馈位数。
在软件实现中，可以使用各种编程语言如C、C++、Python等编写m序列发生器。 软件实现具有灵活度高、易于调试和修改等优点，但也存在运行速度较慢和需 要运行额外的处理器等缺点。
m序列发生器的应用
m序列发生器在信号处理、通信技术等领域具有广泛的应用。以下是m序列发生 器的一些典型应用：

引言伪随机噪声具有类似于随机噪声的某些统计特性，同时又能够重复产生。

由于它具有随机噪声的优点，又避免了随机噪声的缺点，因此获得了日益广泛的实际实用。

这种周期性数字序列称为随机序列，有时又称为随机信号和伪随机码。

m序列是伪随机序列中最重要的序列中的一种，它不但具有易于产生的特点，还具有良好的自相关特性，在扩频通信中得到了广泛的应用。

1. m序列设计方案选择1.1 方案一编程实现m 序列：MA TLAB编程非常简单，无需进行变量声明，可以很方便的实现m序列。

1.2方案二图1.1 Simulink 实现m 序列Simulink 实现m 序列(如图1.1所示) 。

Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。

在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可构造出复杂的系统。

Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点，并基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。

通过比较方案一和方案二，发现方案一的优点具有通用性，其中mserises.m相当于一个通项，根据具体的本原多项式调用它即可，而方案二利用MATLAB的simulink直接搭建模块，在移位寄存器较少时利用此方法极为简单，可是当移位寄存器的数量增多时，要搭建那么多的模块就显得很繁琐，缺乏通用性。

2.Simulink工具介绍2.1 Simulink简介Simulink是MATLAB软件最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。

在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可以构造出复杂的系统。

Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点，并基于以上优点Simulink已被广泛应用与控制理论和数字信号处理的复杂仿真和设计。

同时有大量的第三方软件和硬件可应用于或被要求应用于Simulink。

第1章 基于伪随机序列的传输处理综合设计1.1 伪随机序列伪随机序列包括m 序列、Gold 序列、M 序列和组合序列等，其中最常用到的是m 序列[5,6]。

本文根据m 序列完成了传输处理系统的综合设计。

1.1.1 m 序列的生成m 序列是线性反馈移位寄存器的最大长度序列。

它的生成可用移位寄存器序列发生器的特征多项式来确定，其特征多项式()F x 可以定义为：20120()...ni n i n i F x C x C C x C x C x ===++++∑ （2－1） 其中x 的幂次表示元素相应的位置。

根据代数理论的严格证明，当特征多项式()F x 满足以下3个条件时就一定能够产生m 序列：（1）()F x 是不可约的，即不能再分解因式； （2）()F x 可整除1p x +，这里21n p =-； （3）()F x 不能整除1q x +，这里q p <；目前广泛应用的m 序列都是由移位寄存器构成的。

如图2－1所示，m 序列发生器由n 个二元存储器和模2开关网络组成。

二元存储器通常是一种双稳态触发器，它的两种状态记为0和l ，其状态取决于时钟控制下输入的信息(0或1)，例如第i 级移位寄存器的状态取决于时钟脉冲后的第i 一1级移位寄存器的状态。

图中C i 表示为反馈线的两种可能连接状态：C i ＝1表示连接线连通，即第n －i 级输出加入到反馈中；C i ＝0表示连接线断开，即第n －i 级输出未参加到反馈中。

图2－1由于移位寄存器的初始状态是随机的，它可能是1，也可能是0。

如果各级移位寄存器的初始状态都为0时，则模2加法器的输出将始终为0，这样就不能产生任何序列。

为了防止这种情况发生，在图2－1中往往还需要增加必要的检测电路。

1.1.2 m 序列的特性分析m 序列由n 级移位寄存器产生的m 序列，其周期为21n -。

m 序列具有如下的一些特性：1) 随机性：在m 序列的一个周期中，0和1出现概率大致相同，0码只比1码多一个，且1的个数为121n --，0的个数为12n -。

第1章绪论1.1 课题背景在信息化社会，通信系统担负着信息传输、交换和处理的重要任务。

通信技术的发展代表了一个国家科学技术的发展现状，也成为国家经济发展的一个重要推动力。

扩展频谱通信是通信的一个重要分支和发展方向，它是扩展频谱技术和通信技术相结合的产物。

由于扩展频谱即使具有抗干扰能力强、截获率低、多址能力强、抗多径、保密性好及测距能力强等一系列的优点，使得扩展频谱通信越来越受到人们的重视。

随着大规模或超大规模集成电路技术、微电子技术、为处理技术的迅猛发展以及一些新型器件的广泛应用，扩展频谱通信的发展迈上了一个新的台阶，它不仅在军事通信中占有重要地位，而且正迅速地渗透到民用通信中。

可以毫不夸张地讲，在现代通信系统，特别是无线通信系统，没有扩展频谱技术，这些系统想生存都是比较困难的。

在扩展频谱系统中，伪随机序列起着重要的作用。

在直扩系统中，用伪随机序列将传输信息扩展，在接收时又用它将信息压缩，并使干扰信息功率扩展，提高了系统的抗干扰能力；在跳频系统中，用伪随机序列控制频率合成器产生的频率随机地跳变，躲避干扰；在跳时系统中，用伪随机序列控制脉冲发送的时间和持续时间。

由此可见，伪随机序列性能的好坏，直接关系到整个系统性能的好坏，是一个至关重要的问题。

m序列是最长线性移位寄存器序列，是伪随机序列中最重要的序列中的一种，这种序列易于产生，有优良的自相关特性。

在直扩系统中m序列用于扩展要传递的信号，在跳频系统中m序列用来控制跳频系统的频率合成器，组成随机跳频图案。

电子设计技术由于计算机技术的发展而产生了巨大变化。

本设计是利用电子设计方法，用电路图表示设计思想，用实验电路板搭载实验电路，进行模拟、仿真，用电子测试仪器进行功能、性能测试。

20世纪80年代，计算机辅助设计（CAD）技术开始发展，许多CAD工具软件开始流行。

在信息学科领域也和其他学科一样，计算机辅助设计技术步入了发展轨道。

由于电子科学是计算机科学的基础，计算机学科的发展离不开电子学科的支持，但是计算机科学又反作用于电子科学，加速了电子学科的发展。

end behavioral;
8
序列发生器的功能仿真波形的建立
9
计数型序列信号发生器
• 以同步计数器为基础； • 例：设计产生序列信号为1111000100的发生器； • 序列长度M=10，选用一个模10的同步计数器
10
计数型序列信号发生器
Q3 Q2 Q1 Q0 F
0
0
0
0
1
0
0
0
1
1
0
0
1
0
map(clk,t0,set,reset,t00,t01); U2:Dtrigger port
map(clk,t00,set,reset,t10,t11); U3:Dtrigger port
map(clk,t10,set,reset,t20,t21); t0<=t11 and t21; q<=t20; nq<=not t20;
移存型序列信号发生器
• 第一步：根据要求列真值表和状态图
• 第二步：根据真值表画卡诺图，求次态方程；
•
Q1n+1=not(Q3n.Q2n)
• 第三步：检查系统能否自启动；
• 第四步：确定触发器类型和数目；
• 第五步：确定逻辑电路图；
7
移存型序列信号发生器
entity shiftxuilie is port(clk:in bit;
成M个状态组合，完成状态转移； • 求出移位寄存器的串行输入激励函数，即可构成
该序列信号的产生电路。
• 例：设计产生序列信号为11000的发生器
5
移存型序列信号发生器
序号 Q3 Q2 Q1 0110 1100 2000 3001 4011
110

基于FPGA的ｍ序列发生器摘要ｍ序列广泛应用于密码学、通信、雷达、导航等多个领域，本文提出了一种基于FPGA的伪随机序列产生方法，应用移位寄存器理论从序列的本原多项式出发，获得产生该序列的移位寄存器反馈逻辑式，结合FPGA芯片结构特点，在序列算法实现中采用元件例化语句。

算法运用VHDL语言编程，以A1tera的QuartusⅡ软件为开发平台，给出了序列的仿真波形。

序列的统计特性分析表明：该方法产生的序列符合ｍ序列的伪随机特性，验证了算法的正确性。

关键词：ｍ序列；移位寄存器理论；VHDL语言1 m序列m序列是伪随机序列的一种 ,结构简单 ,实现方便。

在现代工程实践中 , m 序列在通讯、导航、雷达、通信系统性能的测量等领域中有着广泛的应用。

例如 , 在连续波雷达中可用作测距信号 , 在遥控系统中可用作遥控信号 , 在多址通信中可用作地址信号 , 在数字通信中可用作群同步信号 ,还可用作噪声源及在保密通信中起加密作用等。

伪噪声发生器在测距、通信等领域的应用日益受到人们重视。

目前，m序列产生实现方法主要有3种：(1)门电路实现该方法设计简单，但随移位寄存器级数的增长，电路装调困难，且占用的印制板面积较大。

(2)DSP编程实现该方法专业性过强，不适合一般用户。

(3)VHDL与CPLD实现由于CPLD的高集成度，而且VHDL语言编程较为方便，故可以大大减少电路的装调的困难。

文章提出VHDL语言实现，，l序列电路是周期、初相位可编程变化的，其应用较为灵活，通过微处理器对其进行适当的初始化，即可产生用户所需周期、初相位的m序列输出。

用软件方式构成的特点是采用灵活的数据查询方式可以获得任意级数 n 的本原多项式系数 ,从而实现 m 序列的产生 , 但速度受到单片机工作速度的限制。

而 FPGA 具有硬件电路实现的优点 , 又具有设计上的灵活性 , 并且由于FPGA 便于实现大规模的数字系统。

1.1 理论基础m 序列是最长线性反馈移位寄存器序列的简称，它是由带线性反馈的移位寄存器产生的周期最长的一种序列。

基于EWB的序列信号发生器分析和设计前言在当今电子设计领域，EDA设计和仿真是一个十分重要的设计环节。

在众多的EDA设计和仿真软件中，EWB软件以其强大的仿真设计应用功能，在各高校电信类专业电子电路的仿真和设计中得到了较广泛的应用。

EWB软件及其相关库包的应用对提高学生的仿真设计能力，更新设计理念有较大的好处。

EWB（电子工作平台）软件，最突出的特点是用户界面友好，各类器件和集成芯片丰富，尤其是其直观的虚拟仪表是EWB软件的一大特色。

它采用直观的图形界面创建电路：在计算机屏幕上模仿真实实验室的工作台，绘制电路图需要的元器件、电路仿真需要的测试仪器均可直接从屏幕上选取。

EWB软件所包含的虚拟仪表有：示波器，万用表，函数发生器，波特图图示仪，失真度分析仪，频谱分析仪，逻辑分析仪，网络分析仪等。

这些仪器的使用使仿真分析的操作更符合平时实验的习惯。

本次毕业设计主要是利用EWB软件来设计和仿真序列信号发生器，并结合理论进一步验证序列信号发生器的实际作用。

1 EWB软件的简介1.1 EWB软件的概述随着电子技术和计算机技术的发展，电子产品已与计算机紧密相连，电子产品的智能化日益完善，电路的集成度越来越高，而产品的更新周期却越来越短。

电子设计自动化（EDA）技术，使得电子线路的设计人员能在计算机上完成电路的功能设计、逻辑设计、性能分析、时序测试直至印刷电路板的自动设计。

EDA是在计算机辅助设计（CAD）技术的基础上发展起来的计算机设计软件系统。

与早期的CAD软件相比，EDA软件的自动化程度更高、功能更完善、运行速度更快，而且操作界面友善，有良好的数据开放性和互换性。

电子工作平台Electronics Workbench (EWB)(现称为MultiSim) 软件是加拿大Interactive Image Technologies公司于八十年代末、九十年代初推出的电子电路仿真的虚拟电子工作台软件，它具有这样一些特点：（1）软件仪器的控制面板外形和操作方式都与实物相似，可以实时显示测量结果。

1 引言本文的主要内容是移位寄存器74LS194的研究和m序列码发生器的产生原理以及基于MAX+PLUS II、Protel 99SE软件的实现。

m序列码发生器的产生原理和实现是CDMA通信中的核心，具有重要的理论价值和广阔的应用前景。

文中基于对74LS194移位寄存器的研究，对伪随机序列的特性及对m序列发生器的结构进行了分析，运用MAX+PLUS II的模拟仿真和Protel 99SE进行印刷电路板设计，验证其正确性，最终产生m序列码。

1.1 研究此课题的目的伪随机序列系列具有良好的随机性和接近于白噪声的相关函数，并且有预先的可确定性和可重复性。

这些特性使得伪随机序列得到了广泛的应用。

1.2 伪随机序列的应用和意义1.2.1在通信加密中的应用m序列自相关性较好，容易产生和复制，而且具有伪随机性，利用m序列加密数字信号使加密后的信号在携带原始信息的同时具有伪噪声的特点，以达到在信号传输的过程中隐藏信息的目的；在信号接收端，再次利用m序列加以解密，恢复出原始信号[1]。

1.2.2 在雷达信号设计中的应用近年兴起的扩展频谱雷达所采用的信号是已调制的具有类似噪声性质的伪随机序列，它具有很高的距离分辨力和速度分辨力。

这种雷达的接收机采用相关解调的方式工作，能够在低信噪比的条件下工作，同时具有很强的抗干扰能力。

该型雷达实质上是一种连续波雷达，具有低截获概率性，是一种体制新、性能高、适应现代高技术战争需要的雷达。

采用伪随机序列作为发射信号的雷达系统具有许多突出的优点。

首先，它是一种连续波雷达，可以较好地利用发射机的功率。

其次，它在一定的信噪比时，能够达到很好的测量精度，保证测量的单值性，比单脉冲雷达具有更高的距离分辨力和速度分辨力。

最后，它具有较强的抗干扰能力，敌方要干扰这种宽带雷达信号，将比干扰普通的雷达信号困难得多[2]。

1.2.3 在通信系统中的应用伪随机序列是一种貌似随机，实际上是有规律的周期性二进制序列，具有类似噪声序列的性质，在CDMA中，地址码都是从伪随机序列中选取的，在CDMA中使用一种最易实现的伪随机序列：m序列，利用m序列不同相位来区分不同用户；为了数据安全，在CDMA的寻呼信道和正向业务信道中使用了数据掩码（即数据扰乱）技术，其方法是用长度为2的42次方减1的m序列用于对业务信道进行扰码（注意不是扩频），它在分组交织器输出的调制字符上进行，通过交织器输出字符与长码PN码片的二进制模工相加而完成。