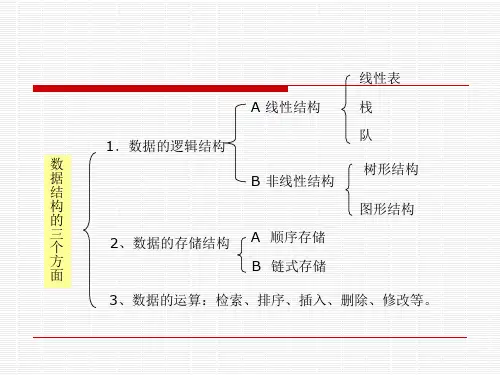
线性表
A 线性结构
栈
队 1.数据的逻辑结构
数 据
树形结构 B 非线性结构
结
构
图形结构
的
三 个
2、数据的存储结构 A 顺序存储
方 面
B 链式存储
3、数据的运算:检索、排序、插入、删除、修改等。
第六章 树和二叉树
6.1 树的定义和基本术语 6.2 二叉树
6.2.1 二叉树的定义 6.2.2 二叉树的性质 6.2.3 二叉树的存储结构
TraverseTree ( T,Visit() ) ; 初始条件:树t存在, Visit是对结点操作的应用函数。 操作结果:按某种次序对T的每个结点调用函数Visit ()一次且至 多一次。一旦Visit ()失败,则操作失败。
堂兄弟——其双亲在同一层的结点互为堂兄弟。K L
M
结点的层次(level)——从根结点算起,根为第一层,它的孩子为第二层…。
深度(depth)——树中结点的最大层次数。
森林(forest)——m(m0)棵互不相交的树的集合。
树的抽象数据类型定义:
ADT Tree{ 数据对象D:D是具有相同特性的数据元素的集合。 数据关系R:若D为空集,则称为空树; 若D仅含一个数据元素,则R为空集,否则R={H},H是如下二元关系: (1)在D中存在唯一的称为根的数据元素root,它在关系H下无前驱; (2)若D-{root}≠Ф,则存在D-{root}的一个划分D1, D2, ..., Dm (m>0),对任意j≠k(1≤j,k≤m)有Dj∩Dk=φ ,且对任意 的i(1≤i≤m),唯一存在数据元素xi∈Di,有<root,xi> ∈ H; (3)对应于D-{root}的划分,H-{<root,x1>,....,<root,xm>} 有唯一的一个划分H1 , H2 ,..., Hm (m>0),对任意j≠k (1≤j,k≤m)有Hj∩Hk=Ф ,且对任意的i(1≤i≤m),Hi 是Di上 的二元关系,(Di ,{Hi})是一棵符合本定义的树,称为根root的子 树。