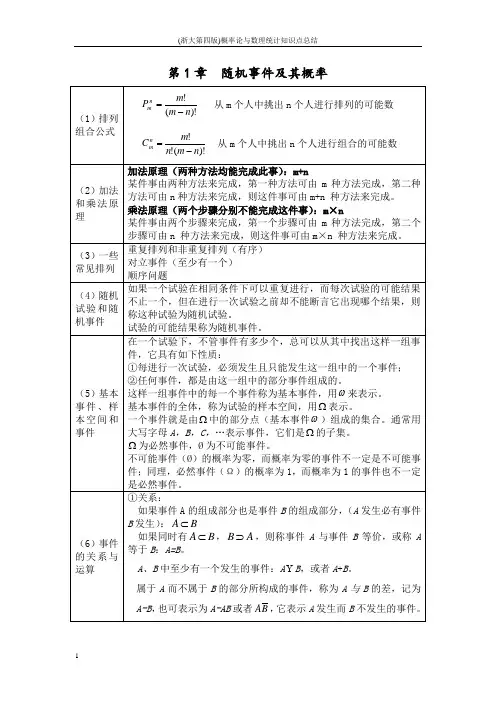
(4.1)
i,j 1, 2, 3,
则有E(Z) E g(X, Y) g(x i ,y j )p ij , (4.2) (假设级数绝对收敛)
例. 设随机变量(X, Y)的概率密度为 3 , 1 y x.x 1 x 3 2 f(x,y) 2x y 0, 其它, 1 试求 : E(Y),E( ) XY
e
1 x
dx
1 t x
2
0
t 2 e t dt 22 ,
D(X) E(X2 ) -[ E(X)]2 2 .
30 正态分布: 设X~N(, 2 ), 则
解 : E(X)
2
t2 2
1
xe
t2 2
-
(x )2 22
例. 二项分布的均值的计算: 设X~b(n,p),引入r.v.Xi(i=1, 2, …, n), 它们是相互独 立的且都服从0--1分布: P{Xi=1}=p, P{Xi=0}=q, X表 示n次独立重复试验中A发生的次数,Xi表示第i次试 验的结果:Xi=1表示A发生, Xi=0表示A不发生, 所以
解: 计算X1的均值, 由定义有 E(X1) =00+1 0.2+2 0.8=1.8 E(X2)=00.6+1 0.3+2 0.1=0.5
显然,乙的成绩比甲的差.
例2. 有2个相互独立工作的电子装置, 它们的寿命Xk (k 1, 2 )服从同一指数分布, 其概率密度为:
x 1 e , x 0, f(x) θ 0, 0, x 0,
i
n
故 E(X) np D(X) npq.