下载文档原格式
双线性变换法的原理
双线性变换法是一种通过将问题转化成一对线性方程组求解的方法，常用于解决二元二次方程或二元二次函数的问题。
其原理可以归纳如下：
1. 假设我们要解决一个二元二次方程或二元二次函数的问题，形式为ax² + bxy + cy² + dx + ey + f = 0（或f(x, y) = 0）。
2. 首先，对于该方程的每一项，我们引入一个新的变量u和v，并将该项表示为一个新的线性方程。
例如，对于ax²，我们将
其表示为au²。
3. 在引入新的变量后，我们得到了一组新的线性方程，形式为Aui + Bvi + Ci + Di + Ei + F = 0，其中i表示第i个线性方程。
4. 接下来，我们要构造一组满足上述线性方程的两个二次式，即f(u, v) = 0。
这里，我们选择f(u, v) = Au² + Buv + Cv² + Du
+ Ev + F。
5. 由于方程组中的每一个线性方程都对应一个二次式，我们可以得到关于u和v的二元二次方程。
我们需要求解这个二元二次方程，从而得到u和v的值。
6. 一旦找到了u和v的值，我们可以将其代入到原方程中，得到x和y的值，从而解决了原始的二元二次方程或二元二次函数问题。
双线性变换法的核心思想是通过引入新的变量，将一个二次式转化为一组线性方程，从而将原问题转化为一对线性方程组，利用线性方程组的解法来求解原问题。
这种方法的优势在于可以利用线性方程组求解的方法解决二次方程或二次函数的问题，而线性方程组求解的方法已经非常成熟和广泛应用。
双线性变换法双线性变换法(bilinear transofrmation method)是一种通过变换以分析和解决非线性系统的复杂方法。
它最初由Collins，Mitroff和Zinnes提出，其主要特点是将非线性系统转化为线性系统来进行分析。
它把一个非线性系统映射到一个线性系统可以使一些复杂的非线性图像变成简单的线性图像，从而形成简单的表达式来解决复杂的问题。
一、双线性变换法定义双线性变换法是指通过线性常数和相关系数，将一维和多维数据变换为更简单的线性形式，以模拟复杂的非线性系统的运算的一种变换方法。
二、双线性变换法的应用（1）控制论领域。
双线性变换可以将复杂的非线性系统转变为简单的线性系统，使得这些复杂的系统容易控制。
（2）视觉领域。
双线性变换可以解决计算机视觉中的误差传播问题，将非线性的图像识别问题转变为简单的线性问题来处理；另外，在图像处理领域用双线性变换可以实现图像的变换，从而实现复杂的图像变换；（3）机器学习领域。
双线性变换可以将非线性的机器学习问题变换为线性的问题，让算法可以更加简单有效地解决复杂的机器学习问题。
三、双线性变换法的局限性（1）双线性变换法还有一些困难。
例如，当非线性系统出现很多两个变量或多个变量间有联系时，双线性变换也会受到很大影响。
（2）双线性变换法也会遇到数值不稳定的问题，在遇到非线性系统的情况下，很多变量的变化对结果的影响会变得很大，因此会产生数值不稳定的现象。
（3）双线性变换只是一种模拟，它并不能完全模拟出非线性系统的真实行为，因此很多时候双线性变换的结果可能不太准确。
双线性变换法是一种实用性很强的方法，它可以帮助我们更准确地分析和解决非线性系统问题，它也应用于控制论、视觉和机器学习等领域，但由于它有一些限制，如数值不稳定性和无法完全模拟非线性系统，因此我们需要更加谨慎地运用双线性变换法来真正发挥它的优势。
双线性变换法（Bilinear Interpolation）是在图像处理中常用的一种插值方法。
公式如下：
f(x,y) = (1-x)(1-y)f(0,0) + (1-x)yf(0,1) + x(1-y)f(1,0) + xyf(1,1)
其中x,y 为目标像素坐标在原图像坐标系中的坐标值，f(0,0),f(0,1),f(1,0),f(1,1) 分别表示目标像素周围4 个像素点的灰度值。
双线性变换法是一种通过线性变换来求解目标像素点灰度值的方法。
它通过对图像进行缩放或旋转时，对于输出图像中缺失的像素点进行插值，来解决图像变形导致的像素点缺失问题。
双线性变换法是一种非常高效的插值方法，其计算量与像素点数量无关。
另外，它还具有较高的精度和较低的计算复杂度。
它在图像处理、图像识别、图像分析、图像压缩等领域有着广泛的应用。
双线性变换法是一种双线性插值法，它基于线性插值法，通过对目标像素周围4个像素点的灰度值进行线性变换来求出目标像素点的灰度值。
其优点是插值效果好，像素质量高，图像变形较小。
双线性变换法在图像缩放、旋转、矫正等操作中都有着广泛的应用。
它在图像处理中常用来解决图像变形导致的像素点缺失问题。
此外还可以用于从低分辨率的图像中重建高
分辨率图像，并且在视频处理中也有着广泛的应用。
河北XX大学课程设计报告学生姓名：学号：专业班级：课程名称：数字信号处理学年学期：学年第学期指导教师：2 0 11 年月课程设计成绩评定表目录一、设计题目二、设计目的三、设计原理四、实现方法五、设计内容及要求六、设计结果及改进建议七、思考题八、设计体会九、参考文献一、设计题目用双线性变换法设计IIR数字滤波器二、设计目的1.熟悉IIR数字滤波器的原理与方法。
2.掌握数字滤波器的计算机仿真方法。
3.通过观察对实际心电图信号的滤波作用，获得数字滤波的感性知识。
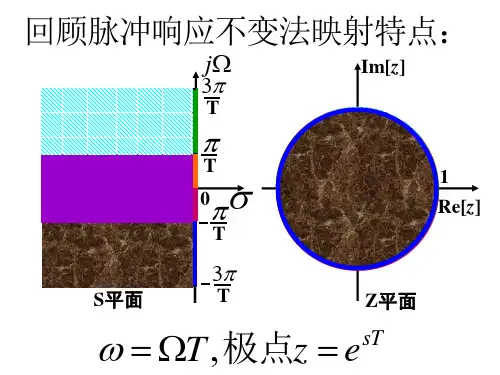
三、设计原理1、双线性变换法采用非线性频率压缩方法，将整个频域轴上的频率范围压缩到-π/T~π/T之间，再用z=e sT转换到z平面上。
也就是说，第一步现将整个S平面压缩映射到S1平面的-π/T~π/T一条横带里；第二步再通过标准变换关系1e S T将此横带变换到整个z平面上去。
这样就使S平面与Z平面建立了一一对应的胆汁关系，消除了多只变换性，也就消除了频谱混叠现象，映射关系如图所示。
Z平面为了将S平面的整个虚轴jΩ压缩到S平面轴上的-π/T到π/T段上，1可以通过以上的正切的变换实现Ω=2/Ttan(1ΩT/2)（1-1）式中，T 仍是采样间隔。
当1Ω由-π/T 经过0变化到π/T 时，Ω由-∞经过0变化到+∞，也即映射了整个j Ω轴。
将上式（1-1）写成111122222TTj j TTj j e e j TeeΩΩΩΩ--Ω=∙+ （1-2）将此关系解析延拓到整个S 平面和1S 平面，令j Ω=s, 1j Ω=S1,则得111221tan()21es Ts TS T e TT--==∙+(1-3)再将S1平面通过以下标准变换关系映射到Z 平面：z=S1T e （1-4） 从而得到S 平面和Z 平面的单值映射关系为;11211Z S T Z---=+(1-5) 122122T T S SZ T T SS++==--(1-6)式（1-5）和式（1-6）是S 平面与Z 平面之间的单值映射关系，这种变换都是两个线性函数之比，因此成为双线性变换。
