第三讲 eviews多元线性回归模型

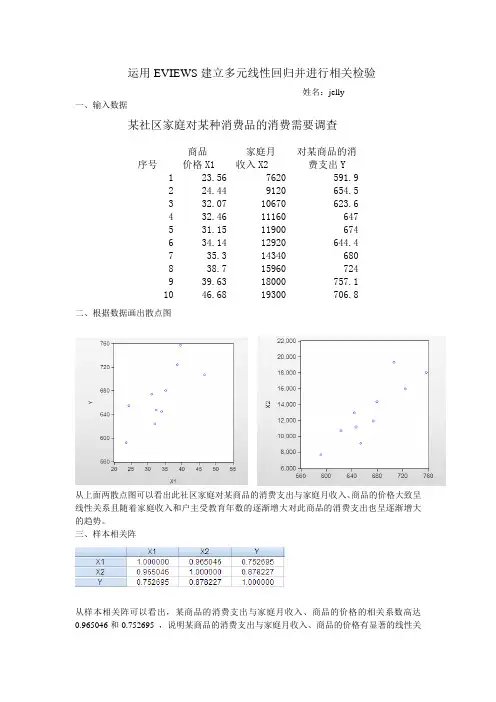
运用EVIEWS 建立多元线性回归并进行相关检验姓名：jelly一、输入数据某社区家庭对某种消费品的消费需要调查二、根据数据画出散点图从上面两散点图可以看出此社区家庭对某商品的消费支出与家庭月收入、商品的价格大致呈线性关系且随着家庭收入和户主受教育年数的逐渐增大对此商品的消费支出也呈逐渐增大的趋势。

三、样本相关阵从样本相关阵可以看出，某商品的消费支出与家庭月收入、商品的价格的相关系数高达0.965046和0.752695 ，说明某商品的消费支出与家庭月收入、商品的价格有显著的线性关序号 商品 价格X1 家庭月 收入X2 对某商品的消费支出Y 1 23.56 7620 591.9 2 24.44 9120 654.5 3 32.07 10670 623.6 4 32.46 11160 647 5 31.15 11900 674 6 34.14 12920 644.4 7 35.3 14340 680 8 38.7 15960 724 9 39.63 18000 757.1 10 46.68 19300 706.8系，可以考虑建立二元线性回归模型。

四、对数据进行普通最小二乘估计，OLS 表如下五、写出估计方程12626.50939.7905700.28618i Y X X ∧=-+（40.13010） （3.197843） （0.05838）t=(15.611195) (-3.061617) (4.902030)20.902218R = 2R =0.874281 六、随机干扰项2'1e e n k σ∧=--'''''ˆˆˆˆˆ()()()()e e Y YY Y Y X Y X Y Y Y X βββ=--=--=-=2116.85 所以22116.85ˆ302.411021σ==-- 由OLS 表得20.902218R = 2R =0.874281 七、由OLS 可得 F=32.29 0.05(2,7) 4.74F =因为32.29>4.74,所以方程的总体线性性显著成立由OLS 表可得 C 的t 值为15.61 X1的t 值为-3.06 X2的值为4.90 0.025(7) 2.365t =所以常输项，X1和X2的总体参数都显著的异于零将数据分别代入以下三个式子：0ˆ00.025ˆt S ββ±⨯ 1ˆ10.025ˆt S ββ±⨯ 2ˆ20.025ˆt S ββ±⨯ 可得参数95%的置信区间分别为（531.62，724.40） -17.35，-2.22） （0.014，0.042）八、X1=35 X2=20000将X1，X2代人方程可得Y 为856.20Y 的均值0ˆY S =37.05 0.025(7) 2.365t = 所以Y 的均值在95%的置信区间为（768.58，943.82）Y 的个值0ˆY S =40.93 0.025(7) 2.365t =所以Y 的个值在95%的置信区间为（759.41，952.99）第二个实验输入数据，对其进行回归分析输出OLS 表由表可得方程为ˆln 101540.609ln 0.361ln Y K L =++ （1.59）（3.45） （1.79）2R =0.8099 2R =0.7963 F=59.660.05(2,28)F =3.34 0.025(28)t =2.048 0.01(28)t =1.701所以lnK 与lnL 联合起来对lnY 有显著的线性影响在5%的显著性水平下，lnK 的参数通过了检验但lnL 的参数未通过t 检验，如果设定显著性水平为10%，lnL 与lnK 都通过检验。

第三章多元线性回归模型案例分析一、研究目的1提出问题：研究中国税收收入增长的主要原因(必须要有研究的意义，且具创新价值)2分析问题：从宏观经济看经济增长是税收增长的源泉；公共财政的需求；物价水平；税收政策（要注重经济理论的相关性和逻辑性）二、模型设定1被解释变量：为了全面反映中国税收增长的全貌，选择包括中央和地方的的“国家财政收入”中的各项税收作为被解释变量2解释变量：选择“国内生产总值GDP”作为经济整体增长水平的代表；选择中央和地方“财政支出”作为公共财政需求的代表，选择“商品零售物价指数”作为物价水平的代表，而由于财政体制的改革难以量化，且1985年后财税体制改革对税收增长影响不是很大，故暂不考虑。

3设定线性模型为：Y t= β1+β2X2t+β3 X3t+β4 X4t +u t注：X1默认为14经济理论构造成功之后，即着手收集数据资料（这要借助统计学的知识进行整理，并不是什么数据都可以直接拿来用。

首先，数据来源的权威性，即必须保证数据的准确可靠性，不能随意捏造，其次，数据的合理分类，最后是数据的合理运用）附：数据三、估计参数利用eviews3.0进行分析1建立工作文件新建工作文档：file-new-workfile，在打开的workfile range 对话框中的workfile frequency 中选择annual，start date 输入1978，end date输入2002，点击ok。

2输入数据直接在命令窗口输入“data Y X2 X3 X4 、、、”本案例中输入data Y X2 X3 X4然后是将excel中的数据复制过来，并点击name命名GROUP01。

3估计参数直接在命令窗口输入“LS Y C X2 X3 X4 、、、”。

LS是做最小二乘估计的命令，Y为被解释变量，C为截距项，X为解释变量，注意LS Y C X之间要有空格，被解释变量紧接在命令LS之后。

本案例中输入LS Y C X2 X3 X4 本题中得到下表，点击name 命名eq01。

一.模型设定本例中我们假设拟建立如下多元回归模型：01122Y X X u βββ=+++二.估计参数1.建立工作文件首先，进入Eviews 主页，在菜单中依次点击File\New\Workfile ，出现对话框Work Create 。

截面数据Unstructured/undated 只需输入样本数就可以。

时间序列数据Dated-regular frequency 在Date specification 中选择数据频率： Annual （年度） Weekly （周数据） Quarterly (季度)Daily （5 day week ）每周5天日数据 Daily （7 day week ）每周7天日数据 Monthly （月度） integer date （未注明日期或者不规则的） Semi Annual （半年度）其次，点击OK ，出现未命名文件的Workfile UNTITLED 工作框。

其中c 为截距项，resid 为残差项。

若要将文件存盘，点击save ，在save as 对话框中选择存盘路径，并输入文件名。

如多元线性回归案例2.输入数据方法一：Quick\Empty Group 等方法二：data Y X1 X2,得到如下表;3.估计参数方法一：Quick\Estimate Equation 方法二: LS Y C X1 X2三、解释表里参数标准差1β∧S =0.075308，回归标准差=被解释变量标准差=回归模型标准差：σ∧残差平方和：2i e ∑=4170093被解释变量的标准差：2=2388.459 AIC 和SC 准则：这两个准则要求仅当所增加的解释变量能减少AIC 值或SC 值时才在原模型中增加该解释变量。

与调整的可决系数相似。

多元小于一元，可以将前期人均居民消费作为解释变量包括在模型中。

四、模型检验1.经济意义检验估计的参数值都为正数，经济意义合理。

所估计的参数120.555644,0.250085ββ∧∧==，说明在2006年可支配收入不变的情况下，2005年消费支出每增加1元，平均来说，可导致2006年消费支出提高0.250085元。

第三课一元及多元线性回归模型一元线性回归模型一、做两个变量的散点图，从而看两个变量是否具有线性关系。

案例数据：1985-2002年我国人均钢产量与人均GDP的时间序列数据（数据3_1_1）。

操作方法：通过序列组的形式右键单击打开后，在group窗口下view——graph---scatter，通过对散点图结同样的操作可以检验其它案例数据（3_1_2和3_1_3）的特征：案例数据2、3、4、5：10个家庭人均收入与消费支出的横截面数据；1978-2000年中国人均消费模型；1978年-2008年北京市城镇居民年家庭收入和年消费性支出数据（case1_1的数据）； 1970年-1980年美国的咖啡平均真实零售价格（每磅美元）与消费量（每人每日杯数）（其中，零售价格是已经经过物价调整的）二、通过建立方程对象的方式来估计一个方程，并保存我们建立的方程对象。

Workfile窗口下建立新的对象---equation对象并命名，在equation estimation 窗口下的specification 选项卡下的equation specification对话框中设置因变量、自变量及常数项，在estimation settings对话框中注意：建模途径：command: quick\estimation equation回车，或object\equation object,设置。

命令行形式：（1）列表法：consp c gdpp 或（2）公式法：consp=c(1)+c(2)*gdpp三、方程估计结果的解释、评价及模型检验（拟合优度评价，估计参数和方程的显著性检验）消费方程中，C为自发性消费，x（gdpp）的系数为经济参数，关注其意义；通过拟合优度、调整后的拟合优度、t统计量后的精确显著性水平p（相伴概率）；f统计量的p来判断对原假设接受与否四、在回归估计结果中显示方程的三种形式（即估计命令，回归方程的一般表达式，带有系数估计值的表达式）Estimation Command:LS GDPP STEELP CEstimation Equation:GDPP = C(1)*STEELP + C(2)Substituted Coefficients:GDPP = *STEELP - 3394.五、如何查看因变量的实际值、拟合值和回归方程的残差（包括表的形式和图的形式）通过方程窗口下的view去实现实际值、拟合值和回归方程的残差；单独显示残差及标准化后的对于案例数据1978年-2008年北京市城镇居民年家庭收入和年消费性支出数据，进行样本内与外的预测。

多元回归分析案例——中国税收增长的分析一、研究的目的要求改革开放以来，随着经济体制改革的深化和经济的快速增长，中国的财政收支状况发生很大变化，中央和地方的税收收入1978年为519.28亿元，到2002年已增长到17636.45亿元，25年间增长了33倍，平均每年增长%。

为了研究影响中国税收收入增长的主要原因，分析中央和地方税收收入的增长规律，预测中国税收未来的增长趋势，需要建立计量经济模型。

影响中国税收收入增长的因素很多，但据分析主要的因素可能有：（1）从宏观经济看，经济整体增长是税收增长的基本源泉。

（2）公共财政的需求，税收收入是财政收入的主体，社会经济的发展和社会保障的完善等都对公共财政提出要求，因此对预算支出所表现的公共财政的需求对当年的税收收入可能会有一定的影响。

（3）物价水平。

我国的税制结构以流转税为主，以现行价格计算的GDP等指标和经营者的收入水平都与物价水平有关。

（4）税收政策因素。

我国自1978年以来经历了两次大的税制改革，一次是1984-1985年的国有企业利改税，另一次是1994年的全国范围内的新税制改革。

税制改革对税收会产生影响，特别是1985年税收陡增215.42%。

但是第二次税制改革对税收增长速度的影响不是非常大。

因此，可以从以上几个方面，分析各种因素对中国税收增长的具体影响。

二、模型设定为了全面反映中国税收增长的全貌，选择包括中央和地方税收的“国家财政收入”中的“各项税收”（简称“税收收入”）作为被解释变量，以反映国家税收的增长；选择“国内生产总值（GDP）”作为经济整体增长水平的代表；选择中央和地方“财政支出”作为公共财政需求的代表；选择“商品零售物价指数”作为物价水平的代表。

由于财税体制的改革难以量化，而且1985年以后财税体制改革对税收增长影响不是很大，可暂不考虑税制改革对税收增长的影响。

所以解释变量设定为可观测的“国内生产总值”、“财政支出”、“商品零售物价指数”等变量。

第三课一元及多元线性回归模型3.1一元线性回归模型一、做两个变量的散点图，从而看两个变量是否具有线性关系。

案例数据：1985-2002年我国人均钢产量与人均GDP的时间序列数据（数据3_1_1）。

操作方法：通过序列组的形式右键单击打开后，在group窗口下view——graph---scatter，通过对散点图结同样的操作可以检验其它案例数据（3_1_2和3_1_3）的特征：案例数据2、3、4、5：10个家庭人均收入与消费支出的横截面数据；1978-2000年中国人均消费模型；1978年-2008年北京市城镇居民年家庭收入和年消费性支出数据（case1_1的数据）； 1970年-1980年美国的咖啡平均真实零售价格（每磅美元）与消费量（每人每日杯数）（其中，零售价格是已经经过物价调整的）二、通过建立方程对象的方式来估计一个方程，并保存我们建立的方程对象。

Workfile窗口下建立新的对象---equation对象并命名，在equation estimation 窗口下的specification 选项卡下的equation specification对话框中设置因变量、自变量及常数项，在estimation settings对话框中注意：建模途径：command: quick\estimation equation回车，或object\equation object,设置。

命令行形式：（1）列表法：consp c gdpp 或（2）公式法：consp=c(1)+c(2)*gdpp三、方程估计结果的解释、评价及模型检验（拟合优度评价，估计参数和方程的显著性检验）消费方程中，C为自发性消费，x（gdpp）的系数为经济参数，关注其意义；通过拟合优度、调整后的拟合优度、t统计量后的精确显著性水平p（相伴概率）；f统计量的p来判断对原假设接受与否四、在回归估计结果中显示方程的三种形式（即估计命令，回归方程的一般表达式，带有系数估计值的表达式）Estimation Command:LS GDPP STEELP CEstimation Equation:GDPP = C(1)*STEELP + C(2)Substituted Coefficients:GDPP = 93.6876362857*STEELP - 3394.97191614五、如何查看因变量的实际值、拟合值和回归方程的残差（包括表的形式和图的形式）通过方程窗口下的view去实现实际值、拟合值和回归方程的残差；单独显示残差及标准化后的对于案例数据1978年-2008年北京市城镇居民年家庭收入和年消费性支出数据，进行样本内与外的预测。

第三章 多元线性回归模型一、名词解释1、多元线性回归模型：在现实经济活动中往往存在一个变量受到其他多个变量影响的现象，表现在线性回归模型中有多个解释变量，这样的模型被称做多元线性回归模型，多元是指多个解释变量2、调整的可决系数2R ：又叫调整的决定系数，是一个用于描述多个解释变量对被解释变量的联合影响程度的统计量，克服了2R 随解释变量的增加而增大的缺陷，与2R 的关系为2211(1)1n R R n k -=----。

3、偏回归系数：在多元回归模型中，每一个解释变量前的参数即为偏回归系数，它测度了当其他解释变量保持不变时，该变量增加1单位对被解释变量带来的平均影响程度。

4、正规方程组：采用OLS 方法估计线性回归模型时，对残差平方和关于各参数求偏导，并令偏导数为0后得到的方程组，其矩阵形式为ˆX X X Y β''=。

5、方程显著性检验：是针对所有解释变量对被解释变量的联合影响是否显著所作的检验，旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出判断。

二、单项选择题1、C ：F 统计量的意义2、A ：F 统计量的定义3、B ：随机误差项方差的估计值1ˆ22--=∑k n e iσ4、A ：书上P92和P93公式5、C ：A 参看导论部分内容；B 在判断多重共线等问题的时候，很有必要；D 在相同解释变量情况下可以衡量6、C ：书上P99，比较F 统计量和可决系数的公式即可7、A ：书P818、D ：A 截距项可以不管它；B 不考虑beta0；C 相关关系与因果关系的辨析 9、B ：注意！只是在服从基本假设的前提下，统计量才服从相应的分布10、D ：AB 不能简单通过可决系数判断模型好坏，还要考虑样本量、异方差等问题；三、多项选择题1、ACDE ：概念性2、BD ：概念性3、BCD ：总体显著，则至少一个参数不为04、BC ：参考可决系数和F 统计量的公式5、AD ：考虑极端情况，ESS=0，可发现CE 错四、判断题、 1、√2、√3、×4、×：调整的可决系数5、√五、简答题 1、 答：多元线性回归模型与一元线性回归模型的区别表现在如下几个方面：一是解释变量的个数不同；二是模型的经典假设不同，多元线性回归模型比一元线性回归模型多了个“解释变量之间不存在线性相关关系”的假定；三是多元线性回归模型的参数估计式的表达更为复杂。

第三章 多元线性回归模型第一节 多元线性回归模型及基本假定问题：只有一个解释变量的线性回归模型能否满足分析经济问题的需要？简单线性回归模型的主要缺陷是：把被解释变量Y 看成是解释变量X 的函数是前提是，在其它条件不变的情况下，并且，所有其它影响Y 的因素都应与X 不相关，但这在实际情况中很难满足。

怎样在一元线性回归的基础上引入多元变量的回归？ 看教科书第72—73页关于汽车销售量的影响因素的讨论。

一、多元线性回归模型的意义1、建立多元线性回归模型的意义，即一元线性回归模型的缺陷，多个主要影响因素的缺失对模型的不利影响。

在一元线性回归模型中，如果总体回归函数的设定是正确的，那么，根据样本数据得到的样本回归模型就应该有较好的拟合效果，这时，可决系数就应该较大。

相反，如果在模型设定时忽略了影响被解释变量的某些重要因素，拟合效果可能就会较差，此时可决系数会偏低，并且由于忽略了一些重要变量而对误差项的影响会加大，这时误差项会表现出一些违背假定的情况。

2、从一个解释变量到多个解释变量的演变。

一个生产函数的例子，一个商品需求函数的例子，（教材第74页）。

二、多元线性回归模型及其矩阵表示1、一般线性回归模型的数学表达式。

设 12233i ii k k ii Y XXXu ββββ=+++++i=1，2，3，…，n在模型表达式里，1β仍是截距项，它反映的是当所有解释变量取值为零时，被解释变量Y 的取值；j β（j=2，3，…，k ）为斜率系数，它的经济含义：在其它变量不变的情况下，第j 个解释变量每变动一个单位，Y 平均增加（或减少）j β个单位，这就是所谓的运用边际分析法对多元变量意义下回归参数的解释。

因此，称j β为偏回归系数，它反映了第j 个解释变量对Y 的边际影响程度。

4、2、总体回归函数，即12233(|)i i i k ki E Y X X X X ββββ=++++3、样本回归函数，即12233ˆˆˆˆˆi i k k iY X X Xββββ=++++ 4、将n 个样本观测值代入上述表达式，可得到从形式上看，像似方程组的形式。