下载文档原格式
电路中的除法器设计在电路设计中，除法器是一种十分重要的组件。
它可以将输入的数字进行除法运算，将商和余数输出。
除法器在计算机和数字信号处理器等电子设备中被广泛使用，因此其设计和优化具有重要意义。
一、除法器的基本原理除法运算是一种复杂的运算，要实现除法器的设计，首先需要了解其基本原理。
除法器的基本原理是通过移位和减法实现的。
在将被除数和除数输入除法器后，除法器将被除数和除数进行比较，并开始迭代过程。
在每一次迭代中，被除数的位数向左移动，直到其高位与除数相等或超过除数。
然后，除法器进行减法操作，将除数减去被除数，结果作为商的一位。
此后，商持续左移，被减数保持不变，重复上述过程，直到所有的商位都得出。
二、除法器的设计策略在除法器的设计中，有几种常见的策略可以考虑。
1. 组合逻辑除法器：这种类型的除法器使用组合逻辑电路实现，通过减法器、比较器和移位器等组件的组合来实现除法运算。
组合逻辑除法器的优点是速度较快，但缺点是占用较多的电路资源。
2. 串行逻辑除法器：与组合逻辑除法器相反，串行逻辑除法器使用顺序逻辑电路实现。
它通过一个时钟信号，逐位地进行计算，因此典型的串行逻辑除法器速度较慢。
但串行逻辑除法器更节省电路资源，因此在一些资源有限的场景中得到了广泛应用。
3. 重复系列除法器：这种除法器通过多个并行的子除法器实现，并行计算多个位的商。
重复系列除法器具有较高的性能，但需要更多的电路资源和功耗。
三、除法器的优化方法为了提高除法器的性能和效率，可以采用一些优化方法。
1. 位级并行思路：通过将除法器分解为多位的子除法器，并行计算多个子除法器，可以大幅提高除法器的速度。
这种方法在重复系列除法器中得到了广泛应用。
2. 乘法相关技巧：利用乘法器计算除法运算，可以加速除法器的运算速度。
通过将除数进行逆运算，转化为乘法操作，可以利用乘法器的高速性能，提升除法器的效率。
3. 进制转换思想：将数字进行二进制到十进制的转换，然后进行简单的除法运算，可以减少运算的复杂程度，提高除法器的运算速度。
乘法器的工作原理
乘法器是一种用于实现数字乘法运算的电路或器件。
它将两个输入的数字进行相乘，并得到其乘积作为输出。
乘法器的工作原理基于逻辑门电路的组合与串联。
乘法器通常是由多个部分组成的，其中包括乘法器的位数、运算规则以及乘法器内部的逻辑门电路。
这些部分协同工作以实现精确且高效的乘法运算。
在一个典型的乘法器中，输入信号将首先被分为不同的位数。
每一位数将被独立处理，并最终合并以得到最终的乘积结果。
每个位数的处理过程包括了多个逻辑运算，例如与门、或门和异或门。
为了完成乘法运算，乘法器将两个输入位进行逐位相乘。
这里的位可以是二进制位，也可以是十进制位。
逐位相乘的方法可以通过一系列的逻辑门电路来实现。
这些逻辑门电路可以对输入位进行操作，并生成相乘位的输出。
在乘法器中，最低有效位（LSB）的运算最先进行。
在相邻的
位运算完成后，它们的结果会被以并行的方式传递给下一位的运算。
这样一直进行到最高有效位（MSB）的运算完成。
最后，所有位的乘法结果会被整合在一起，形成最终的乘积。
乘法器的性能取决于其位数和逻辑门电路的设计。
更高的位数会产生更精确的乘法结果，但也会增加乘法器的复杂性和功耗。
因此，在设计乘法器时需要权衡精确性和性能之间的关系。
总之，乘法器是一种通过组合逻辑门电路来实现数字乘法运算的电路或器件。
它将输入信号分解为不同的位数，并使用逻辑门电路逐位相乘。
最后，将每个位的乘法结果合并在一起，得到总体的乘积输出。
乘法器原理
乘法器是一种用于执行乘法运算的数字电路。
它通常由多个逻辑门、寄存器和时钟信号组成。
乘法器的主要原理是将两个输入数（被乘数和乘数）进行相乘，然后输出它们的乘积。
乘法器的输入是一系列位（比特），每个位代表一个二进制数。
这些输入位通过逻辑门来实现不同位上的相乘。
一般来说，较高位的输入乘数与较低位的被乘数相乘后，得到的乘积需要左移若干位。
这个左移操作可以通过使用寄存器和时钟信号来完成。
乘法器可以分为多种类型，其中最常见的是布斯乘法器和Wallace树乘法器。
布斯乘法器通过将被乘数和乘数进行分割，并使用部分积和约化乘法器来实现乘法运算。
Wallace树乘法
器是一种高效的乘法器类型，它通过将乘法操作转化为加法操作来提高运算速度。
这种乘法器通常使用布斯乘法器和连锁加法器来实现。
乘法器的输出是乘法的结果，通常也是一系列位（比特）。
输出可以进一步用于其他计算或者存储在寄存器中。
同时，乘法器也可以进一步扩展为多位乘法器，用于执行更大位数的乘法操作。
综上所述，乘法器是一种将两个输入数进行相乘的数字电路。
它的原理是利用逻辑门、寄存器和时钟信号来实现乘法运算。
乘法器可以分为不同类型，其中最常见的是布斯乘法器和
Wallace树乘法器。
乘法器的输出是乘法的结果，通常用于其他计算或者存储在寄存器中。
cpu中用来对数据进行各种算术运算和逻辑运算的部件CPU是计算机的核心部件，它负责执行各种算术运算和逻辑运算，以处理和执行计算机程序中的指令。
CPU中的运算部件是实现这些功能的关键部分。
一、算术运算部件CPU中的算术运算部件主要负责执行加、减、乘、除等算术运算。
这些运算在计算机程序中非常常见，例如在处理数值数据、进行数学计算或执行科学计算时。
1. 加法器：加法器是CPU中最基本的算术运算部件，用于执行加法运算。
它接收两个操作数，并将它们相加，生成结果。
加法器在CPU中通常是多位的，可以处理不同长度的数据。
2. 减法器：减法器与加法器类似，用于执行减法运算。
它接收两个操作数，并将它们相减，生成结果。
3. 乘法器：乘法器用于执行乘法运算。
它接收两个操作数，并将它们相乘，生成结果。
乘法器在CPU中通常是多位的，可以处理不同长度的数据。
4. 除法器：除法器用于执行除法运算。
它接收两个操作数，其中一个作为被除数，另一个作为除数，生成商和余数。
除法器在CPU中通常是多位的，可以处理不同长度的数据。
二、逻辑运算部件CPU中的逻辑运算部件主要负责执行逻辑运算，如与、或、非等。
这些运算在计算机程序中也非常常见，例如在处理布尔逻辑、条件判断或控制流程时。
1. 逻辑与门：逻辑与门用于执行逻辑与运算。
它接收两个操作数，只有当两个操作数都为真时，结果才为真。
2. 逻辑或门：逻辑或门用于执行逻辑或运算。
它接收两个操作数，只要其中一个操作数为真，结果就为真。
3. 逻辑非门：逻辑非门用于执行逻辑非运算。
它接收一个操作数，并对其取反。
如果操作数为真，结果为假；如果操作数为假，结果为真。
除了以上介绍的算术运算和逻辑运算部件外，CPU中还可能包含其他类型的运算部件，如移位器、比较器等，以满足不同的计算需求。
三、总结CPU中的运算部件是实现计算机程序中各种算术和逻辑运算的关键部分。
这些部件通过精心的设计和优化，使得CPU能够高效地完成各种复杂的计算任务。
计算机组成原理实验报告题目：运算器部件实验：除法器学院数学与信息学院学科门类工学专业12软件工程学号2012436138姓名王赛赛指导教师王兵一、实验目的1.掌握乘法器以及booth 乘法器的原理二、实验原理除法是乘法的倒数。
首先我们看一下十进制数的除法。
为了方便起见，我们假定十进制数的各位要么为1要么为0，例如（1001010）10 ÷（1000）： 1 0 0 1 商1000）1 0 0 1 0 1 0 被除数 -1 0 0 01 01 0 11 0 1 0- 1 0 0 01 010 余数被除数、除数、商、和余数的关系如下式所示：被除数=商×除数+余数式中，余数必须比除数小。
除法中求商的基本方法是利用被除数减去除数，看结果是正还是负，来决定商的这位是1还是0。
假定被除数和除数都是正的，因此商和余数都是非负的。
操作数和结果都是32位的，忽略符号。
比较善于节省空间的人们发现，商寄存器浪费的空间正好和余数寄存器浪费的空间一样，因此，将商寄存器和余数寄存器结合起来。
下图为除法器的算法流程。
除数从寄存器左移一位 从余数寄存器左半部分减去除数寄存器，结果存在余数寄存器的左半部分 测试余数 余数寄存器左移一位，第0位置1 余数≥0 加除数到余数寄存器的左半部分已恢复原来的被除数值。
商寄存器左移，第0位置0余数<0 开始No<32三、实验步骤1.打开Quartus->tools->programmer，将booth_divider.sof下载到FPGA中。
注意进行programmer 时，应在program/configure下的方框中打勾，然后下载。
2.在实验台上通过模式开关选择FPGA独立调试模式010。
3.将短路子DZ3短接且短路子DZ4断开，使FPGA-CPU所需要的时钟使用正单脉冲时钟。
四、实验现象本实验实现4位数的除法（无符号除法），输入输出规则对应如下：1、输入的4位被除数（dividend）md3～md0对应开关SD11～SD8。
乘法器原理乘法器是一种用来进行乘法运算的电子元件，它在数字电路中起着非常重要的作用。
乘法器的原理是怎样的呢？让我们一起来探讨一下。
首先，我们需要了解乘法器的基本结构。
乘法器通常由多个逻辑门和触发器组成，其中包括与门、或门、非门等。
这些逻辑门和触发器相互连接，形成了一个复杂的电路结构，用来实现乘法运算。
乘法器的原理可以简单地用一个例子来说明。
假设我们要计算8乘以3的结果。
首先，我们将8和3转换为二进制数，分别为1000和0011。
然后，我们使用乘法器进行计算。
乘法器通过逐位相乘的方式，将每一位上的乘积相加，最终得到最终的乘法结果。
在乘法器的工作过程中，每一个逻辑门都承担着重要的作用。
与门用来进行位与运算，或门用来进行位或运算，非门用来进行位取反运算。
这些逻辑门相互组合，形成了一个高效的乘法器电路。
除了基本的逻辑门，乘法器还包括了触发器。
触发器在乘法器中的作用是非常重要的，它用来存储中间结果，并在计算过程中进行数据传递和控制。
乘法器的原理不仅仅局限于二进制乘法，它还可以应用到其他进制的乘法运算中。
无论是二进制、八进制还是十进制，乘法器都能够高效地进行乘法运算，这正是乘法器在数字电路中被广泛应用的原因之一。
总的来说，乘法器是一种非常重要的数字电路元件，它通过逻辑门和触发器的组合，实现了高效的乘法运算。
乘法器的原理是基于逐位相乘和相加的方式，通过逻辑门的运算和触发器的存储，最终得到乘法的结果。
乘法器不仅可以应用于二进制乘法，还可以适用于其他进制的乘法运算，具有非常广泛的应用价值。
希望通过本文的介绍，读者能对乘法器的原理有一个更加深入的了解。
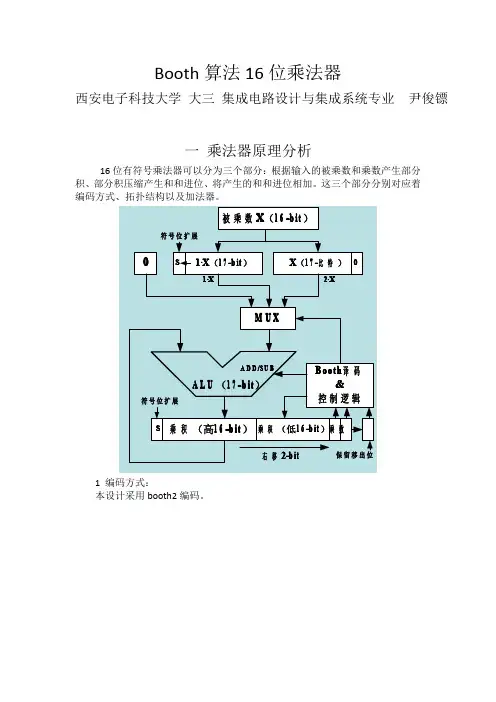
Booth算法16位乘法器西安电子科技大学大三集成电路设计与集成系统专业尹俊镖一乘法器原理分析16位有符号乘法器可以分为三个部分：根据输入的被乘数和乘数产生部分积、部分积压缩产生和和进位、将产生的和和进位相加。
这三个部分分别对应着编码方式、拓扑结构以及加法器。
1编码方式：本设计采用booth2编码。
部分积是负数时S=1，部分积是正数时S=0；当部分积是+0时，E=1，部分积是-0时，E=0，其余情况E=S取反。
2拓扑结构：本设计采用二进制树的拓扑结构。
二进制树拓扑结构排列的较为规整，且部分积压缩的速度也非常快。
部分积压缩的目的是为了减小进位传播的延时，采用进位保留加法器，根据当前位信息产生下一位的进位，仅仅产生而没有进位行波传播，这样就可以把当前的多位压缩到较少的位数。
经过几次压后，把部分积压缩成和以及进位。
部分积主要是通过counter和compressor进行压缩，通常使用（3:2）counter 和（4:2）compressor。
（3:2）counter其实质就是一个全加器，进位输入为ci，进位输出为c；（4:2）compressor可以由两个全加器组成，ci为进位输入，Coin为内部进位，输入到下一位的进位输入Ci，Coex为输出进位。
上图为二进制树的拓扑结构图，每4个部分积输入到一个（4:2）compressor 中，产生两个输出，则8个部分积使用3次（4:2）compressor就可以得到和和进位。
部分积的压缩方式可以见下图。
如图中所示，加上最后一个部分积的进位，共有9个部分积，本设计把最后的进位位移到第一个部分积上，使用5个全加器，把进位融合到第一个部分积，这样就转变成8个部分积了，再使用两级二进制树压缩，所以总共使用了三级压缩，最终得到部分积的和和进位。
为了免去不必要的硬件开销，对于部分积边上的位采用counter压缩。
上文提到的符号位扩展的改进方法，其目的也就是减少硬件开销，所以在不影响性能的情况下，单独出来部分积的边缘位是十分有必要的。
