2012年秋九年级数学期末测试卷(2)

金山区2012学年度第一学期初中九年级数学期末考试2012.1（测试时间：100分钟，满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）1．在Rt △ABC 中，∠C = 90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，如果a =3，b =4，那么下列等式中正确的是（ ） （A ）4sin 3A =； （B ）4cos 3A =； （C ）4tan 3A =； （D ）4cot 3A =． 2．如图，已知AB ∥CD ，AD 与BC 相交于点O ，AO ∶DO =1∶2， 那么下列式子错误的是（ ）（A ）BO ∶CO =1∶2； （B ）CO ∶BC =1∶2； （C ）AD ∶DO =3∶2； （D ）AB ∶CD =1∶2．3．把抛物线2y x =-向下平移2个单位后得到的新抛物线的解析式是（ ） （A ）22y x =--； （B ）22y x =-+； （C ）()22y x =-+； （D ）()22y x =--．4．下列图形中既是轴对称图形，又是中心对称图形的是（ ） （A ）等边三角形； （B ）平行四边形； （C ）正方形； （D ）正五边形．5．下列条件中，不能判定a ∥b的是（ ）（A ）a ∥c ，b ∥c； （B=；（C ）a =b 5-； （D ）（B ）a =c 2，b =c．6．⊙1O 与⊙2O 的半径分别为1和3，那么下列四个叙述中，错误的是（ ） （A ）当1224O O <<时，⊙1O 与⊙2O 有两个公共点； （B ）当⊙1O 与⊙2O 有两个公共点时，1224O O <<； （C ）当0≤122O O <时，⊙1O 与⊙2O 没有公共点； （D ）当⊙1O 与⊙2O 没有公共点时，0≤122O O <．ABCD O（第2题图）二、填空题：（本大题共12题，每题4分，满分48分）7．已知线段b 是线段a 、c 的比例中项，且a = 9，c = 4， 那么b = ． 8．如果两个相似三角形的面积比为1∶4，那么它们的对应角平分线的比为 ． 9．已知点G 是△ABC 的重心，AD 是中线，AG =6，那么DG = ． 10．求值：o o sin 60cot 30⋅= ．11．抛物线()213y x =--的顶点坐标是 ．12．请写出一个以直线2-=x 为对称轴，且在对称轴左侧部分是上升的抛物线，这条抛物线的表达式可以是 ．13．小李在楼上点A 处看到楼下点B 处的小明的俯角是35度，那么点B 处的小明看点A 处的小李的仰角是 度．14．已知点P 在⊙O 外，且⊙O 的半径为5，设OP =x ，那么x 的取值范围是 ． 15．在平面直角坐标系中，以点P （4，3-）为圆心的圆与x 轴相切，那么该圆和y 轴的位置关系是 ． 16．正十边形的中心角度数是 ．17．相切两圆的半径分别是4和6，那么这两个圆的圆心距为 ． 18．在△ABC 中，AB =AC = 5，BC =6，以点A 为圆心，r 为半径的圆与底边BC （包括点B 和点C ）有两个公共点，那么r 的取值范围是 ． 三、解答题：（本大题共7题，满分78分） 19．（本题满分10分）如图，已知两个不平行的向量a 、b．先化简，再求作：113()(2)22a b a b ---．（不要求写作法，但要指出图中表示结论的向量）20．（本题满分10分）已知二次函数2y x m x n =++的图像经过点（2，3-）和（1-，0），求这个二次函数的解析式，并求出它的图像的顶点坐标和对称轴．ba（第19题图）21．（本题满分10分）如图，已知在平行四边形ABCD 中，点E 在边AD 上，线段CE 的延长线与线段BA 的延长线交于点F ，CD =6，AE =12ED ，求BF 的长．22．（本题满分10分）如图是公园中的一个圆弧形拱门，其中拱门的圆心是点O ，拱门的最高处点A 到地面的距离AH =3米，拱门的地面宽BC =2米，求拱门的半径。

20122013年度九年数学期末考卷（含答案）一、选择题（每题4分，共40分）1. 下列选项中，既是有理数又是无理数的是（）A. 0B. πC.D. 1.52. 已知等差数列的前三项分别为a1，a+1，2a+1，则数列的公差为（）A. 2B. 3C. 4D. 53. 下列函数中，奇函数是（）A. y = x²B. y = |x|C. y = x³D. y = x² + 14. 已知三角形ABC的三边长分别为3、4、5，则三角形ABC的面积是（）A. 6B. 8C. 10D. 125. 方程x² + 2x + 1 = 0的解是（）A. x = 1B. x = 0C. x = 1D. x = 1和x = 16. 下列各数中，是无理数的是（）A.B.C.D.7. 下列各式中，正确的是（）A. a² + b² = (a + b)²B. (a + b)² = a² + 2ab + b²C. (a b)² = a² 2ab + b²D. a² b² = (a + b)(a b)8. 已知平行四边形的两条邻边长分别为6cm和8cm，则平行四边形的面积是（）A. 48cm²B. 52cm²C. 56cm²D. 64cm²9. 下列函数中，单调递增的是（）A. y = x²B. y = x²C. y = 2xD. y = 2x10. 已知一组数据的方差是9，那么这组数据的标准差是（）A. 3B. 6C. 9D. 12二、填空题（每题4分，共40分）11. 已知a、b互为相反数，且a + b = 5，则a的值为______。

12. 已知函数f(x) = 2x + 3，当x = 2时，f(x)的值为______。

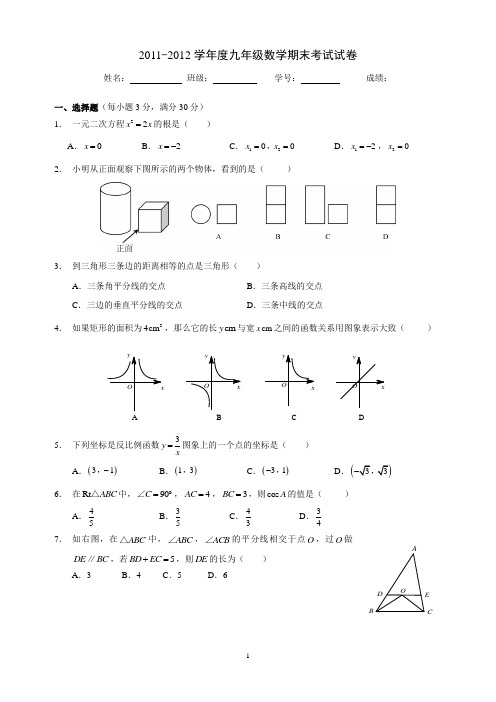
2011-2012学年度九年级数学期末考试试卷姓名： 班级： 学号： 成绩：一、选择题（每小题3分，满分30分） 1． 一元二次方程22x x =的根是（ ） A ．0x =B ．2x =-C ．1200x x ==，D ．12x =-，20x =2． 小明从正面观察下图所示的两个物体，看到的是（ ）3． 到三角形三条边的距离相等的点是三角形（ ）A ．三条角平分线的交点B ．三条高线的交点C ．三边的垂直平分线的交点D ．三条中线的交点4． 如果矩形的面积为24cm ，那么它的长cm y 与宽cm x 之间的函数关系用图象表示大致（ ）A B C D5． 下列坐标是反比例函数3y x=图象上的一个点的坐标是（ ） A ．()31-，B ．()13，C ．()31-，D．(6． 在Rt ABC △中，90C =︒∠，4AC =，3BC =，则cos A 的值是（ ）A ．45B ．35C ．43D ．347． 如右图，在ABC △中，ABC ∠，ACB ∠的平分线相交于点O ，过O 做DE BC ∥，若5BD EC +=，则DE 的长为（ ）A ．3B ．4C ．5D ．6CBE OD A8． 顺次连结四边形各边中点所得到新的四边形是（ ）A ．矩形B ．菱形C ．正方形D ．平行四边形9． 从口袋中随机摸出一球，再放回口袋中，不断重复上述过程，共摸了150次，其中有50次摸到黑球，已知口袋中有黑球10个和若干个白球.由此估计口袋中大约有多少个白球（ ） A ．10个B ．20个C ．30个D ．无法确定10． 若点()11A y -，、()24B y ，、()31C y ，是函数1y x=-图象上的三个点，则下列结论正确的是（ ）A ．123y y y >>B ．321y y y >>C ．213y y y >>D ．312y y y >>二、填空题（每小题3分，满分30分）11． 已知等腰三角形的两边长分别为3cm 、6cm ，则该等腰三角形的周长为 . 12． 计算：tan 45︒= ．13． 已知1x =-是方程260x ax -+=的一个根，则a =_________。

2012年秋季宜昌市（城区）期末调研考试九年级数学试题（全卷三大题24小题 满分：120分时限：120分钟）一、选择题：（每小题3分，共45分）1．如图，桌子上放着一个长方体的茶叶盘和一个圆柱形的水杯，则其主视图是( )2.方程x x 22=的解是( )． A 、x=2 B 、x l =2,x 2=0 C 、0,221==x x ， D 、x=03.已知等腰三角形有两边的长分别为4，9，这个等腰三角形的周长为( ) A 、13 B 、17 C 、22 D 、17或224．如图，在Rt △ABC 中．∠C=90°，AD 是∠BAC 的平分线．DC=2,点D 到AB 边的距离是( )．A 、2 B 、3 C 、4 D 、5 5.如图,已知∠BAD= ∠CAD ，下列条件中，不一定能使△ABD ≌△ACD 的是( )A 、∠B= ∠CB 、∠BDA=∠CDAC 、AB=ACD 、BD=CD6.小伟随机向铺有两种地板砖的地面（如图所示）投掷一个小球，小球落在有花纹的地砖上的概率是( )． A 、154 B 、31 C 、51 D、1527方程x 2+4x-3=0的两个根乘积是( )．A 、3B 、一3C 、4D 、一48、2012年我市民选新闻人物评选展橘期间，在一个有1000人的小区里，老明随机调查了其中的50人，发现有20人看过我市电视台的民选新闻人物先进事迹那么在该小区看过我市 电视台的民选新闻人物先进事迹的人数大约是( )．A 、20B 、40C 、400D 、6009．如图，甲、乙两盏路灯相距20米，一天晚上，当小翔从灯甲底部向灯乙底部直行16米时，发现自己的身影顶部正好接触到路灯乙的底部，己知小翔的身高为l 6米，那么路灯甲的高为( )米． A 、7 B 、8 C 、9 D 、1010．关于x 的一元二次方程x 2-4x+4k=0有两个不相等的实数根，k 的取值范围是( )．A 、k ＞1B 、k ＜lC 、k=l (D)k ≤l ， 11.若依次连接四边形ABCD 各边的中点得到的四边形是菱形，则对角线AC 与BD 需要满足 的条件是( )．A 、垂直B 、相等C 、垂直且相等D 、相互平分12．如图，等腰梯形ABCD 中，AB ∥CD ，AD=BC ，对角线交于点O ，下列结论正确的有( )个．①OA=OB； ② ∠ADO= ∠BCO ； ③∠ODC= ∠OCD A 、O 个 B 、1个 C 、2个 D 、3个 13．反比例函数xk y =第二象限的图象如图所示，过函数图象上一点P 作PA ⊥x 轴于点A ，已知△PAO 的面积为3, k 的值为( )． A 、6 B 、-6 C 、3 D 、-314．如图，在矩形ABCD 中，CD=32．∠DAC=30°，AC 的垂直平分线分别交AD ，AC 于点E 、 D ，连接CE, CE 的长为 15．如图，菱形ABCD 中，AC=6，BD=8，高AE 等于 ．二、解答题（本大题共9小题，共75分）16.直角三角形的三边长度如图所示，求x 的值。

2012年秋华师版九年级数学期末质量抽查试卷（考试时间：120分钟；满分：150分）一、选择题（每小题3分，共21分）1．若二次根式1-x 有意义，则x 的取值范围是（ ）A ．x ≥1B ．x ＞1C ．x ＜1D ．x ≤1 2．与3是同类二次根式的是（ ）A ．a 3B ．9C ．18D ．313．方程0542=--x x 经过配方后，其结果正确的是（ ）A ．1)2(2=-xB ．1)2(2-=+xC ．9)2(2=-xD ．9)2(2=+x 4．下列判断正确的是（ ）A ．所有的直角三角形都相似B ．所有的等腰直角三角形都相似C ．所有的菱形都相似D ．所有的矩形都相似5．如图，△ABC 中，点D 、E 分别在AB 、AC 边上，则下列条件中，不．一定．．能使△AED ∽△ABC 的是（ ）A ．∠2=∠B B ．∠1=∠C C ．ACAD ABAE = D ．BCDE ABAD =6．如图，在△ABC 中，∠C=90°，BC=6，D 、E 分别在 AB 、AC 上，将△ABC 沿DE 折叠，使点A 落在点A ′处，若A ′为CE 的中点．．，则折痕DE 的长为（ ） A ．1B ．2C ．3D ．4A ．30° B．45° C ．50° D ．60°EA B C D 12（第5题） ABCDA ′ E （第6题）二、填空题（每小题4分，共40分） 8= .9．方程(1)(5)0x x -+=的根是 .10．已知地球表面陆地面积与海洋面积的比约为3∶7．若宇宙中飞来一块陨石落在地球上，则落在陆地上的概率是 ．11. 已知1x =-是方程210x mx ++=的一个实数根，则m 的值是 . 12．已知12a b =，则b a a +的值为 .13．已知一个三角形的三边长分别为5，8，7，则另一个与之相似．．的三角形的三边长可以是 .(任写一组即可)14．如图是某水库大坝的横断面，若坡面AB 的坡度i =1∶1，则斜坡AB 的坡角α= 度.15. 如图，点G 是△ABC 的重心，连结AG 并延长交BC 于点D ，若DG=3cm ，则AG= cm . 16= .17．如图，n 个边长为1的相邻正方形的一边均在同一直线上，点1P 、2P 、3P 、…、n P 分别为边21B B 、32B B 、43B B 、…、1n n B B +的中点，△111P C B 的面积为1S ，△222P C B 的面积为2S 、…、△n n n P C B 的面积为n S . ①1S = ；②n S = .(用含n 的式子表示) 三、解答题（共89分） 18．（9分）计算：1)+ 19．（9分）解方程：22510x x -+= 20．（9分）如图是某超市从一楼至二楼之间电梯的剖面图，已知天花板与地面平行，电梯BC与地面AB 的夹角为25°，点E 为电梯上方天花板的边角，DE ⊥CE ，垂足为D ，CD=5.6m . 姚明身高为2.23m ，他乘电梯时挺直身子，头会碰到天花板边角E 吗？请说明理由.(精确到01.0m )（第20题）（第14题）B AC i =1∶1α（第17题）B B B B B12134P P P P D· A C B G （第15题）21．（9分）2012年4月，受“毒胶囊”事件的影响，某种药品的价格大幅度下调，下调后每盒价格是原价的32，已知下调后每盒价格是10元/盒. （1）（3分）该药品的原价是 元；（2）（6分）4月底，各部门加大了对胶囊生产的监管力度，因此，药品价格开始回升，经过两个月后，该药品价格上调为14.4元/盒. 问5、6月份该药品价格的月平均增长率 是多少？22.（9分）如图，在平面直角坐标系中，△ABC 与△A ′B ′C ′关于点P 位似，且顶点都在格点上. （1）（4分）在图上标出．．位似中心P 的位置，并直接写出点P 的坐标是 ； （2）（5分）求△ABC 与△A ′B ′C ′的面积比．23.（9分）如图，一转盘被等分成三个扇形，上面分别标有1 ，1，2，指针位置固定，转动转盘后任其自由停止后，某个扇形会恰好停在指针所指的位置，得到这个扇形上相应的数．若指针恰好指在等分线上，则需重新转动转盘． （1）（3分）若小静转动转盘一次，则她得到负数的概率为 ；（2）（6分）小宇和小静分别转动转盘一次，若两人得到的数相同，则称两人“不谋而合”．请用列表法(或画树状图)求出两人“不谋而合”的概率．24．（9分）如图，在□ABCD 中，AB=5，BC=8，AE ⊥BC ，垂足为E ，cos B=53. （1）（4分）求AE 的长； （2）（5分）求tan ∠CDE 的值．AEBDC25．（13分)如图，已知：AD ∥BC ，AB ⊥BC ，AB=3cm ，AD=2cm ．点P 是线段AB 上的一个动．点．，连接PD ，过点D 作CD ⊥PD ，交射线BC 于点C ，再过点C 作CE ⊥AD ，交AD 的延长线于点E ． （1）（3分）填空：当AP=2cm 时，PD= cm ；（2）（5分）求CD P D的值；（3）（5分）当△APD 与△DPC 相似时，求线段BC 的长．26．（13分）如图，正方形ABCD 的边AD 与矩形EFGH 的边FG 重合，将正方形ABCD 以1cm /秒的速度沿FG 方向移动，移动开始前点A 与点F 重合. 已知正方形ABCD 的边长为1cm ，FG=4cm ，GH=3cm ，设正方形移动的时间为x 秒，且．0≤x ≤5.2． （1）（3分）直接填空：DG= cm (用含x 的代数式表示)； （2）连结CG ，过点A 作AP ∥CG 交GH 于点P ，连结PD ．①（5分）若△DGP 的面积记为1S ，△CDG 的面积记为2S ，则21S S -的值会发生变化吗？ 请说明理由；②（5分）当线段PD 所在直线与正方形ABCD 的对角线AC 垂直时，求线段PD 的长．四、附加题（每小题5分，共10分）友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况，如果你全卷得分低于90分（及格线），则本题的得分将计入全卷得分，但计入后全卷总分最多不超过90分；如果你全卷总分已经达到或超过90分，则本题的得分不计入总分． 1．方程92=x 的根是 .2．如图，从楼顶A 处观测地面B 处的俯角为38°，则从A 处观测B 处的仰角为 °．（第2题）B A38°FB A PE CD。

----完整版学习资料分享----2012年秋季九年级期末跟踪测试数学试题参考答案及评分标准一、选择题（每小题3分，共21分）1．B 2．C 3．D 4．C 5．A 6．D 7．B 二、填空题（每小题4分，共40分）8．x ≥2 9．6 10．3±=x 11．15 12．3213．︒30 14．9 15．2，)2,2( 16． m 6.517．（1）（2分）310 （2）（2分） 5.135.4或 三、解答题（共89分）18．（9分）解：原式＝2223- ……………………6分……………………9分 19．（9分）解：842=-x x ……………………2分222)2(8)2(4-+=-+-x x12)2(2=-x ……………………6分 322±=-x 322±=∴x即3221+=x ，3222-=x ……………………9分20．（9分）解：原式=22344x x x -+++……………………4分 =74+x ……………………6分 当2-=x 时， 原式=7)2(4+-⨯=78+-=1-……………………9分 21．（9分）解：（1）41…………………3分 （2）他们制定的游戏规则是公平的.理由如下: 法一: 画树状图…………………6分2311241344324321----完整版学习资料分享----由树状图可知,共有12种机会均等的情况,其中满足y x >的有6种,P ∴(小明获胜)=21126=,P (小强获胜)=21211=- P ∴(小明获胜)= P (小强获胜)故他们制定的游戏规则是公平的…………………9分 法二：列表…………………6分 由列表可知,共有12种机会均等的情况,其中满足y x >的有6种,P ∴(小明获胜)=21126=,P (小强获胜)=21211=- P ∴(小明获胜)= P (小强获胜)故他们制定的游戏规则是公平的…………………9分 22．（9分）解：（1）如图，△A 1B 1C 1就是所求画的三角形, …………………3分点1A 的坐标为（-1，3）;………………5分（2）由画图可知:四边形B B AA 11为等腰梯形,其中,21=AA ,61=BB ,高为5.∴B B AA S 11=205)62(21=⨯+ …………………9分23．（9分）解：设平均每次下调的百分率为x ，………1分依题意得405)1(5002=-x ……………5分 解得1.01=x ，9.12=x ……………8分因为下调的百分率不可能大于1,所以9.12=x 不合题意舍去,故只取%101.0==x . 答：平均每次下调的百分率为10%． ……………………9分24．（9分）解：过点O 作AB OD ⊥于点D ，…………………1分 ∵OB OA =∴BD AD =D OCA BB 1C C 1()----完整版学习资料分享----∵AB OC //∴︒=∠=∠59AOC OAD …………………3分 在AOD Rt ∆中，OAADOAD =∠cos OAD OA AD ∠⋅=∴cos …………………6分3.11252.0108259cos 22≈⨯⨯≈︒==∴OA AD AB …………………8分 答：支架两个着地点之间的距离AB 约为cm 3.112．…………………9分 25．（13分）解：（1）四边形ABCD 是矩形∴90ADE BCE ∠=∠=︒，AD BC = 又 CE DE = ∴BCE ADE ≅∴AE BE =…………………3分（2）当点E 为CD 中点时，21=BA DE∵四边形ABCD 为矩形∴CD AB //∴21∠=∠，43∠=∠∴PDE ∆∽PBA ∆ ……………5分∴21===BA DE PA PE PB PD 由21=PA PE 可得31=EA PE ……………6分 由（1）知EA EB = 在PBE Rt ∆中，︒=∠90BPE31sin ===∠∴EA PE EB PE DBE ……………8分（3）设AD ＝a在BAD Rt ∆中，︒=∠90BAD ∴222226+=+=a AB AD BD ①……………………9分在EAD Rt ∆中，︒=∠90EDA∴222223+=+=a DE AD AE ②……………………10分①、②联立可得452222+=+a AE BD由（2）知：21==PA PE PB PD ∴PD BD 3=，PE AE 3=……………………11分ABCDEP 13 4 2----完整版学习资料分享----∴452)(9222+=+a PE PD在PDE Rt ∆中，︒=∠90DPE ，则有9222==+DE PE PD994522⨯=+∴a解得23±=a （舍去负值）23=∴AD ……………………12分S AB AD ∴=⋅=13分26．（13分）解：（1）)0,8(A ,)34,0(D ；……………………3分 （2）过点E 作OD EG ⊥于点G ，如图①所示： ∵OAB ∆为等边三角形，AB OC ⊥， ∴OC 平分AOB ∠，∴︒=∠30AOC ，∴903060EOG ∠=︒-︒=︒……………4分∴t EOG OE EG 23sin =∠⋅=…………………5分 又 EG OF S OEF⋅=∆21，t DF OD OF -=-=34 由题意可得：43323)34(21=⋅-t t 解得332±=t ．……………………8分（3）因为FOP BOD ∠=∠，所以应分两种情况讨论：①当︒=∠=∠90BDO FPO 时，如图②， OPF ∆∽ODB ∆，此时OF OE =，∴t t -=34，解得：32=t ．…………………………10分②当︒=∠=∠90ODB OFP 时，OPF ∆∽OBD ∆，如图③，此时，OE OF 21=，∴1)2t t =，AOAOAO----完整版学习资料分享----解得：t =12分 综上所述，当32=t秒或t =秒时，OPF ∆与OBD ∆相似．…………13分。

九年级（上）数学期末质量检测A 卷（共100分）第I 卷（选择题，共36分）一、选择题：本大题共12个小题，每小题3分，共36分。

1、在函数21x y +=中，自变量x 的取值范围是（ ） (A) 1≥x ( B) 1-≤x ( C)11≤≤-x (D) 全体实数 2、下列计算正确的是（ ） (A)2)2(2-=- ( B) 3273-=--( C) )21)(21(-+( D) 35323=+3、已知：1x ，2x 是一元二次方程02=--b ax x 的两根，且1x +2x =2，1x 2x =1- 那么，a ， b 的值分别为（ ）(A) 2=a ，1=b (B) 2-=a ，1=b (C) 2=a ，1-=b (D) 2-=a ，1-=b4、一件商品原价是100元，经过两次优惠后的价格为81元，如果每次优惠的百分率是x 根据题意得x 的值为（ ）A. 5%B.10%C.15%D.20%5、一个不透明的袋子中有n 个出颜色外其余均相同的小球，其中有6个是黄球，每次摸球前将盒子中的球搅匀，任意摸出一个球记下颜色后放回，通过大量试验后发现，摸到黄球的频率稳定在30%，那么可以推算出n 大约是（ ）A. 6B. 10C. 18D. 206、如图，在ABC ∆中，AD 、BE 是两边上的中线且交于O ，则=∆∆BOA EOD S S :( )(A) 1：4 (B ) 1：3 (C) 1： 2 （D ） 2：3 7、 如图，从热气球P 处测得地面A,B 两点的俯角分别是30、 45，如果此时热气球P 处的高度100=PD 米，点BD A 、、在同一条直线上，则B A 、两点的距离是（ ）（A ） 200米 （B ）3200米 （C ）3220米 （D ）)13(100+米 8、下列函数中，当0<x 时，y 随x 的增大而增大的函数是（ ） （A ）x y -= （B ）xy 1=（C ） 12-=x y （D ）22x y -=9、如图，直线l 经过等腰直角三角形ABC 的直角顶点C ， 点B 、A 到直线的距离分别为2和1，则ABC ∆的面积为 （ ） (A) 25 (B)25 (C)5 (D)4510、关于x 的方程0412=--x kx 有实数根，则k 的取值范围是（ ）(A) 1-≥k ( B) 1≥k ( C) 1-≥k 且0=k ( D) 1->k 且0≠k11、在平面直角坐标系中，将抛物线向上（下）或向左（右）平移m 个单位，使平移后的抛物线恰好经过原点，则m 的最小值为（ ）（A ） 1 （B ） 2 （C ） 3 （D ） 412、已知平行四边形ABCD 中， 45=∠DBC ，BC DE ⊥于点E ,CD BF ⊥于点FBFDE 、相交于H ,BF 、HD 的延长线相交于G ，下面结论：①BE DB 2=②BHE A ∠=∠③BH AB = ④BHD ∆相似于BDG ∆ 其中正确的结论是（ ）（A ）①②③④ （B ）①②③ （C ）①②④ （D ）②③④ A第II 卷 （非选择题，共64分）二、填空题：本大题共6个小题，每小题3分，共18分。

2012-2013学年九年级数学上册期末试卷岳池县2012年秋季期末质量检测题九年级数学试卷(全卷满分120分，120分钟完卷)题号一二三四五总分总分人题分3018242820120得分得分评卷人一、选择题：（每小题3分，共30分）在下列各题中，每个题只有一个正确答案，请将正确答案的代号填在括号内。

()1.若是整数，则正整数n的最小值是A.2B.3C.4D.5()2.与的大小关系是A.>B.()3.若a(a-2)-8=0，则a3-1的值为A.63B.-9C.63或-9D.-63或9()4.一个图形无论经过平移还是旋转，有以下说法：①对应线段平行②对应线段相等③对应角相等④图形的形状和大小都没有发生变化其中说法正确的是A.①②③B.①②④C.①③④D.②③④()5.如图，从⊙O外一点P引圆的两条切线PA、PB，切点分别是A、B，如果∠APB=60o，线段PA=10，那么弦AB的长是A.10B.12C.5D.10()6.在Rt△ABC中，∠C=90o，AB=13，AC=12，以B为圆心，6为半径的圆与直线AC的位置关系是A.相切B.相交C.相离D.不能确定()7.下列事件是必然事件的是A.打开电视机，任选一个频道，屏幕上正在播放天气预报B.到电影院任意买一张电影票，座位号是奇数C.在地球上，抛出去的篮球会下落D.掷一枚均匀的骰子，骰子停止转动后偶数点朝上()8.从连续的20个整数中，任意选取一个数，这个数是2的倍数的可能性和它是3的倍数的可能性相比A.3的倍数的可能性大B.2的倍数的可能性大C.两7的可能性相等D.不能确定()9.将抛物线y=4x2向上平移3个单位，再向右平移1个单位，那么得到的抛物线的解析式为A.y=4(x-1)2+3B.y=4(x-1)2-3C.y=4(x+1)2+3D.y=4(x+1)2-3()10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，有下列结论：①a、b同号；②当x=1时和x=3时，函数值相等；③4a+b=0；④当y=-2时，x的值只能取2；⑤当-1其中正确的有A.2个B.3个C.4个D.5个得分评卷人二、填空题：（每小题3分，共18分）11.在一个不透明袋中装有五个除数字外其它完全相同的小球，球面上分别写有0，1，2，3，4这5个数字，玲玲从袋中任意摸出一个小球，球面数字的平方根是有理数的概率是。

2012年初三上册数学期末考试卷2012年初三上册数学期末考试卷1.解答内容一律写在答题卡上，否则不得分.交卷时只交答题卡，本卷不交.2. 答题一律用0.5毫米的黑色签字笔，否则不得分.一、选择题(本大题有7小题，每小题3分，共21分)1.-1的绝对值是( )A.1B.-1C.2D.-22.下列图形中，既是轴对称图形又是中心对称图形的是( )3.一元二次方程2x(x-1)=0的解是( )A.x=2B.x=3C.x=0或x=1D.x=0或x=-14.下列判断正确的是( )A.掷一次骰子，向上的一面是6点B.抛一枚硬币，落地后正面朝上C.抛掷1枚硬币，掷得的结果不是正面朝上就是反面朝上D.“掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就必有1次反面朝上5.一条排水管的截面如图所示，已知排水管的截面半径OB=5，截面圆圆心为O，当水面宽AB=8时，水位高是多少( )A.1B.2C.3D.46.等腰三角形的两边长分别为2和3，则周长为( )A.5B.7C.8D.7或87.如图，直线y=-33x+2与x轴、y轴分别交于A、B 两点，把△AOB绕点A顺时针旋转60deg;后得到△AO’B’，则点B’的坐标是( )A.(4，23)B.(23，4)C.(3，3)D.(23+2，23)二、填空题(本大题有10小题，每题4分，共40分)8.(1)计算：2a-a= . (2) .9.已知ang;A=110deg;，则ang;A的补角的度数是 .10.用科学记数法表示：150000= .11.二次根式有意义，则x的取值范围是____________.12.点P(a，-1)关于原点对称的点P’(b，1)，则a+b=______.13.方程x2-ax+1=0有且只有一个实根，则a的值 .14.如图，AB与CD都是⊙O的直径，ang;AOC=50deg;，则ang;C的度数为_______.15.从分别标有1到9序号的9张卡片中任意抽取一张，抽到序号是3的倍数的概率是_________.16.已知x=-1是一元二次方程x2+mx+n=0的一个根，则m2-2mn+n2的值为__________.17.如图，在平面直角坐标系中，已知点A(-3，0)，B(0，4)，对△AOB连续作旋转变换，依次得到三角形①，②，③，，那么第⑤个三角形离原点O最远距离的坐标是，第2012个三角形离原点O最远距离的坐标是 .三、解答题(本大题有9小题，共89分)18.(本题满分18分)(1)计算：|-1|+128+(-3.14)0-(12)-1.(2)解方程： .(3)如图，在平行四边形ABCD中，E为BC中点，AE 和延长线与DC的延长线相交于点F.证明：△ABE ≌△FCE.19.(本题满分7分) 抛掷一枚均匀的硬币2次，请用列表或画树状图的方法抛掷的结果都是正面朝上的概率.20.(本题满分8分)若ab=4，则称a与b是关于2的“比例数”;(1)2关于2的比例数是________; -2与___________是关于2的比例数;(2)若x1、x2是方程x2+(m-4)x+m2+3=0的两根，且x1、x2是关于2的比例数，试求m的值.21.(本题满分8分)如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：(1)将△ABC向右平移3个单位长度再向下平移2个单位长度，画出两次平移后的△A1B1C1;(2)将△A1B1C1绕C1逆时针旋转90deg;，画出旋转后的△A2B2C1，求线段B1C1旋转过程中扫过的面积(结果保留pi;).22.(本题满分8分)如图，在△ABC中，AB=AC，以AC 为直径的半圆O分别交AB、BC于点D、E.(1)求证：点E是BC的中点;(2)若ang;COD=80deg;，求ang;BED的度数.23.(本题满分8分)某商店准备进一批小电风扇，单价成本价40元，经市场预测，销售定价为52元时，可售出180个;定价每增加1元，销售量将减少10个;反之，定价每下降1元，销售量将增加10个.(1)设定价增加x元，则增加后的价格为元，单价利润是元，销售量为个;(2)若商店预计获利2000元，在尽可能让利给顾客的前提下，定价应调整为多少元?(3)通过调整定价，商店能否获利2260元的利润?若能，求出调整后的定价;若不能，请说明理由.24.(本题满分9分)已知：关于x的一元二次方程mx2-(3m+2)x+2m+2=0(mgt;0).(1)求证：方程有两个不相等的实数根;(2)方程的两个实数根分别为x1，x2(x1求这个函数的解析式;(3)在(2)的条件下，结合函数的图象回答：当自变量m的取值范围满足什么条件时， .25.(本题满分11分)在平面直角坐标系中.过一点分別作坐标轴的垂线，若与坐标轴围成矩形的周长与面积相等，则这个点叫做和谐点.例如.图中过点P分別作x轴，y 轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等，则点P是和谐点.(1)判断点M(l，2)，N(4，4)是否为和谐点，并说明理由;(2)若和谐点P(a，3)在直线y=-x+b(b为常数)上，求a，b 的值26.(本题满分12分)一个反比例函数的图像经过点A(1，3)，O是原点，(1)点B是反比例函数图像上一点，过点B做BCperp;x轴于C，做BDperp;y轴于D，四边形OCBD的周长为8，求OB长.(2)作直线OA交反比例函数图像于点A’，在反比例函数图像上是否存在点P(记横坐标为m)使得△APA’面积为2m?若存在，求P的坐标，若不存在，请说明理由.。

2012年下学期期末考试九年级试题数 学一、选择题（每小题3分，共24分）1、一元二次方程2560x x --=的根是 （ ） A ．x 1=1，x 2=6 B ．x 1=2，x 2=3 C ．x 1=1，x 2=-6 D ．x 1=-1，x 2=62、掷一枚硬币两次，每次都出现正面向上的概率是（ ）A 、21 B 、41 C 、43D 、无法确定 3、某一时刻太阳光下身高1.5m 的小明的影长为2m ，同一时刻旗杆的影长为6m ，则旗杆的高度为（ ）A 、4.5mB 、8mC 、5.5mD 、7m 4、已知5,13b a ba ab -=+则的值是（ ） A 、32 B 、23 C 、49 D 、945、下列命题：① 方程x x =2的解是x =1 ② 4的平方根是2③ 有两边和一角相等的两个三角形全等④ 连接任意四边形各边中点的四边形是平行四边形 其中是真命题的有（ ）个A. 4个B. 3个 C 2个 D. 1个6、设,a b 是方程2220120x x +-=的两个实数根，则a b +的值为（ ） A ．2B ．-2C ．2012D ．-20127、如图，在BE AD ABC ,中，∆是两条中线，则=∆∆ABC EDC S S :（ ）A ．1∶2B ．2∶3C ．1∶3D ．1∶48、如图，在△ABC 中，∠C ＝90°，将△ABC 沿直线MN 翻折后，顶点C 恰好落在AB 边上的点D 处，已知MN ∥AB ，MC ＝6，NC ＝MABN 的面积是（第8题图）NM D A CBA． B． C．D．二、填空题（每小题3分，共24分）9、已知x = 1是一元二次方程02=++n mx x 的一个根，则222n mn m ++的值为 ． 10、若方程240x x m -+=有两个实数根，则m 的取值范围是 。

11、命题“直角三角形的两锐角互余”的逆命题是_____________________________________ 12、两个相似多边形的面积的和等于1562cm ,且相似比等于2：3，则较大多边形的面积是 2cm 。