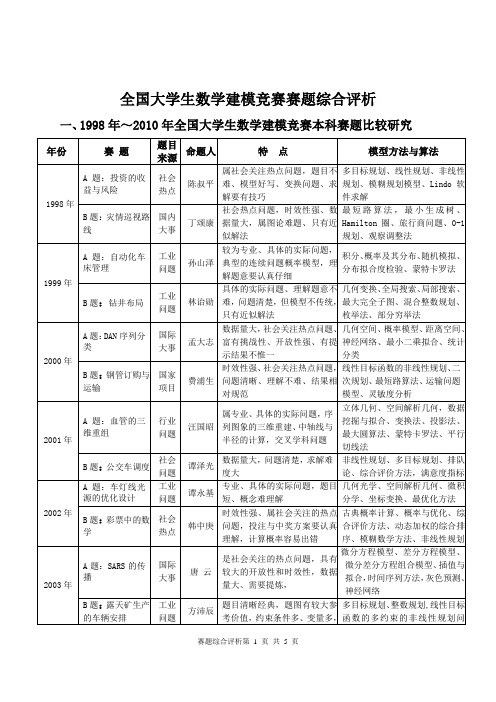
自动化车床模型(数学建模)
- 格式:doc
- 大小:353.50 KB
- 文档页数:15



数学建模自动化车床管理数学建模:自动化车床管理一、引言自动化车床管理是现代制造业中的重要环节,通过合理的管理和优化,可以提高生产效率和产品质量。
为了实现自动化车床管理的科学化、规范化和高效化,需要进行数学建模分析,以便找到最优的管理策略和决策方案。
二、问题描述在自动化车床管理中,存在以下几个关键问题需要解决:1. 生产计划优化问题:如何合理安排车床的生产计划,以最大程度地提高生产效率和资源利用率?2. 设备故障预测问题:如何通过数学建模分析,提前预测车床的故障情况,以便及时进行维修和更换?3. 零部件供应链优化问题:如何通过数学建模分析,优化零部件的供应链管理,以确保及时供应和减少库存成本?三、数学建模方法针对上述问题,可以采用以下数学建模方法进行分析和求解:1. 线性规划模型:通过建立生产计划优化的线性规划模型,考虑生产能力、设备利用率、订单需求等因素,以最大化产量和利润为目标,确定最优的生产计划。
2. 时间序列分析模型:通过对历史数据进行时间序列分析,建立车床故障预测的模型,包括趋势分析、季节性分析、残差分析等,以便提前预测故障情况,采取相应的维修和更换措施。
3. 随机优化模型:通过建立供应链的随机优化模型,考虑供应商的可靠性、交货时间、库存成本等因素,以最小化总成本为目标,确定最优的零部件供应链管理策略。
四、数据收集和处理为了进行数学建模分析,需要收集和处理以下数据:1. 生产数据:包括车床的生产能力、设备利用率、订单需求等数据。
2. 故障数据:包括车床的故障记录、维修时间和维修费用等数据。
3. 供应链数据:包括供应商的可靠性、交货时间、库存成本等数据。
通过对以上数据进行整理和处理,可以得到适用于数学建模的数据集。
五、模型求解和结果分析根据收集和处理的数据,运用上述数学建模方法,可以进行模型求解和结果分析。
具体步骤如下:1. 建立数学模型:根据问题描述,建立相应的数学模型,包括目标函数、约束条件等。

零件检查的数学模型1问题重述1.1需要解决的问题一道工序用自动化车床连续加工某种零件,由于刀具损坏等原因该工序会出现故障,其中刀具损坏故障占95%, 其它故障仅占5%。
工序出现故障是完全随机的, 假定在生产任一零件时出现故障的机会均相同。
工作人员通过检查零件来确定工序是否出现故障。
现积累有100次刀具故障记录,故障出现时该刀具完成的零件数如附录表一。
现计划在刀具加工一定件数后定期更换新刀具。
问题:假定工序故障时产出的零件均为不合格品,正常时产出的零件均为合格品, 试对该工序设计效益最好的检查间隔(生产多少零件检查一次)和刀具更换策略。
2模型的假设及符号说明2.1模型的假设假设1:假设在生产任一零件时出现故障的机会均相等。
假设3:假设生产任一零件时所需的时间相同。
假设4:假设提供的刀具故障记录数据是独立同分布的.假设5:假设提供的刀具故障记录数据是独立同分布的。
2.2符号说明符号说明μ刀具平均寿命σ样本方差Tc检查零件的单位时间间隔T定期换刀的单位时间间隔TT(c)以检测时间间隔为时,系统工序合格零件的单位期望损失cf(x)系统的失效概率密度F(x)累积失效概率密度,即寿命分布函数3问题分析在自动化车床生产流程中,由于刀具损坏等原因会使工序出现故障,工序故障的出现是完全随机的。
工作人员通过检验零件来确定是否出现故障,并且决定在刀具加工一定的零件后更换刀具。
当发生故障时要及时维修,如果检修周期太长,故障不能及时发现,会给生产带来损失;检查周期太短又会增加费用。
在理论上我们首先将问题转化为概率模型。
通过分析题目所给的100次刀具故障记录,我们通过绘图分析假设刀具的寿命服从正态分布。
再通过假设检验,我们决定接受这一假设。
问题中我们建立离散型随机事件模型I 。
我们选择一个周期T 。
目标函数要求目标函数取最小值的情况下求解检查间T 系统工序的期望总损失总=C 系统工序产生的合格零件数U隔和道具更换策略。
U 总分为两种情况:故障发生在换刀之前与故障发生在换刀之后。

机床任务分配问题数学建模任务分配到机床摘要本⽂解决的是机床⽣产调度的问题,⽬的是使产品加⼯路径的组合优化。
对于本⽂所研究的机床任务的合理调度问题,由于⽣产⽅式的不确定,我们根据A,B,C,D这4道⼯序是否有序进⾏了分类研究,并分情况得到了最优解或近似最优解,制定出了不同情况下的合理调度⽅案。
对于问题⼀:在⼯序⽆序的情况下,问题转化为⼀个指派问题,以完成任务耗时最长的那台机床的运⾏时间作为指标,以该指标最⼩作为⽬标函数,建⽴了⼀个0-1整数规划模型,⽤Lingo求解得最短加⼯时间为233h各机床加⼯时间的均衡度为3.8%。
在⼯序有序的情况下,问题⼀转化为⼀个柔性作业车间调度问题,此时⽣产调度的任务就是:确定产品的加⼯路径和每⼀⼯序的加⼯开始时间,并使产品通过系统的时间(Makespan)最⼩。
运⽤遗传算法建⽴模型,绘制出最佳调度的⽢特图,并得到加⼯时间的近似最优解为250h,各机床加⼯时间均衡度为1.6%,均衡度很⾼;与⽆序情况所得最优解相⽐,其近似度为92.7%,具有较好的有效性。
对于问题⼆:在⼯序⽆序的情况下,该问题仍为⼀个指派问题,在加⼊调度费⽤与运⾏费⽤的条件下,我们利⽤理想点法将这两个指标的双⽬标问题转化为单⽬标规划模型来进⾏求解,建⽴了⼀个0-1整数规划模型,⽤Lingo求解得加⼯时间为510h,总费⽤为1784600元。
在⼯序有序的情况下,我们运⽤蚁群算法建⽴模型,经过选⼯序,计算加⼯⼯序k的机床的空闲时间段和加⼯序列,计算可选⼯序的EAPT和信息素的积累等过程,得到加⼯时间为441h,总费⽤为1799000元。
为了进⼀步分析该算法的有效性,我们还进⾏了实例规模较⼤的计算机仿真试验。
我们在模型的改进和推⼴⾥对模型四提出了⼀种评价⽅法,⼒求使⼀群算法的精度进⼀步提⾼,以实现更⼤规模的应⽤。
关键词:指派问题柔性调度理想点法遗传算法蚁群算法1.问题重述1.1问题背景车间⽣产调度是制造系统的基础,⽣产调度的优化⽅法是先进制造技术的核⼼技术。
数控机床的数学模型与仿真技术数控机床是机械加工行业中非常重要的设备之一,它能够通过程序控制来完成精密加工,使得生产效率和产品质量都得到了非常大的提升。
而这种精密性能的实现,离不开数学模型和仿真技术的支持。
一、数学模型在数控机床中的应用数学模型在数控机床中的应用是非常广泛的,它们可以描述不同的物理过程,如机床结构的运动、切削过程的力学和热学、刀具的损耗和磨损等等。
这些模型一般是基于物理定律和经验公式建立的,通过计算机程序来求解。
下面我们具体介绍一下数学模型在数控机床中的几个应用。
1. 机床结构运动机床结构运动是数控机床中最基本的数学模型之一,它描述了机床各部分的位置、速度、加速度随时间的变化。
这个模型是机床控制系统的基础,控制系统通过控制各驱动装置的运动来实现加工程序的执行。
机床结构运动模型的求解需要考虑多种因素,如机床的结构、驱动装置的特性、工件的形状等等,通常使用有限元分析或者正逆动力学模型来求解。
2. 切削过程力学模型切削过程力学模型是研究刀具与工件之间力学相互作用的数学模型,它可以描述刀具的进给、切削和退出过程中的切削力和其他作用力。
这个模型可以帮助设计和选择刀具,优化切削参数,以及预测刀具寿命和工件表面形貌等,它是数控加工中非常重要的数学模型之一。
普遍用的刀具力模型包括切削力系数法、影响系数法、弹性回复切削力模型等。
3. 切削过程热学模型切削过程热学模型是描述切削过程中的热处理过程的数学模型,它可以预测切削面温度和刀具温度等。
这个模型可以帮助优化切削参数,提高切削速率、降低刀具磨损、减少工件变形和提高表面质量等。
切削过程热学模型主要包括经验模型和物理模型。
经验模型通常基于实验数据,通过适当的修正,可以很好地预测切削温度和刀具温度。
物理模型则基于热传导、热应力等物理理论,需要更大的计算开销,但是可以准确地反映热传导和热应力的特性。
二、数控机床仿真技术数控机床仿真技术是基于数学模型的的数字仿真技术,它可以模拟机床的运动、加工过程和性能。
自动化车床管理模型摘要本文研究的是自动化车床管理中定期检查和预防性保全刀具问题。
在现代技术下,被动地等待故障发生,然后投入较高资金处理出现的问题,这种传统的处理方法已经不符合工业生产和现代社会的发展要求。
为解决此问题,我们共建立两个模型,使自动化车床管理方略更科学、更合理。
对于问题一:我们通过一定的数学方法,巧妙地建立了生产每一个零件的平均损失费用L (包括预防保全费用1L , 检查费用2L , 和故障造成的不合格品损失和修复费用3L ,即123LLLL =++)关于刀具定期更换间隔a 的单变量函数关系,并利用MATLAB 等数学计算工具和多种方法,对a 进行逐个赋值,最终得到:当342a =件时,L 取得最小值min 5.297L =元,再根据a 与固定检查间隔n 之间的函数关系得到:16n =件。
对于问题二:此问中效益函数计算的费用与第一问相比,增加了错误判断带来的损失费用,我们将因误判带来的费用考虑到生产每一个零件的平均损失费用L 中,用与第一问类似的模型求解,得到当299a =件时,L 取得最小值min 7.381L =元,对应固定检查间隔18n =件。
对于问题三:保持问题二的情况,我们建立新的模型,并采取连续检查多个零件(最多3次)的方法,降低误判率,从而达到减少每个零件的平均管理费用,使模型更优化。
最终得到在工序发生故障时误判率为0.208,比检查一次的误判率0.4减少0.192,误判率减小了50%;在工序正常时误判率为0.000792,比检查一次的误判率0.02减少0.019208,误判率降低了96.04%,从而使模型得到优化。
关键词:自动化车床管理 效益函数 正态分布 误判率1.问题重述一道工序用自动化车床连续加工某种零件,由于刀具损坏等原因该工序会出现故障,其中刀具损坏故障占95%, 其它故障仅占5%。
工序出现故障是完全随机的, 假定在生产任一零件时出现故障的机会均相同。
工作人员通过检查零件来确定工序是否出现故障。
现积累有100次刀具故障记录,故障出现时该刀具完成的零件数如附表。
现计划在刀具加工一定件数后定期更换新刀具。
已知生产工序的费用参数如下:故障时产出的零件损失费用 f=200元/件;进行检查的费用 t=10元/次;发现故障进行调节使恢复正常的平均费用 d=3000元/次(包括刀具费);未发现故障时更换一把新刀具的费用 k=1000元/次。
要求解的问题:1)假定工序故障时产出的零件均为不合格品,正常时产出的零件均为合格品, 试对该工序设计效益最好的检查间隔(生产多少零件检查一次)和刀具更换策略。
2)如果该工序正常时产出的零件不全是合格品,有2%为不合格品;而工序故障时产出的零件有40%为合格品,60%为不合格品。
工序正常而误认有故障停机产生的损失费用为1500元/次。
对该工序设计效益最好的检查间隔和刀具更换策略。
3)在2)的情况, 可否改进检查方式获得更高的效益。
附:100次刀具故障记录(完成的零件数) (见附录1)2.模型假设和符号说明2.1模型的假设1.换刀间隔和检查间隔很短,这段时间内产生的零件数可以忽略;2.检查时一旦发现不合格品生产立即停止;3.假设该工序只需用一个刀具;4.工序出现故障是随机的,且加工每个零件时出现故障的概率相同。
2.2符号说明3. 问题分析本题研究的是自动化车床管理中定期检查和预防性保全刀具问题。
由于发现故障进行调节使恢复正常的平均费用和故障时产出的零件损失费用较高,而检查费用和更换刀具费用较低,因此,在未进行定期检查和预防性更换刀具时损失费用明显要高,更新管理后,要确定最优的管理方案,得到合适的检查间隔和刀具更换策略,即刀具定期更换间隔和检查间隔,使损失费用最少。
我们选择建立一个效益函数L (生产每个零件的平均损失费用),通过求L 最小值来确定刀具定期更换间隔a 和生产检查间隔n 。
针对问题一:因为效益函数L 包括预防保全费用1L , 检查费用2L , 和故障造成的不合格品损失和修复费用3L (即123L LLL =++),我们按每个零件分摊,分别列式子算出1L 、2L 、3L 求和。
在求解1L 、2L 、3L 过程中,根据样本数据确定刀具寿命的经验分布或拟合分布F (x ),并且得到相关参数,确定无预防性更换刀具时刀具故障的平均间隔和采取有预防性更换策略时刀具故障间隔的表达式,同时利用n 与a 之间的函数关系进行转换,最后得到L 关于刀具定期更换间隔a 的单变量函数,可通过取不同的步长a 逐个求出L 的值,找到L 的最小值和对应的a 值,并通过所得a 求出对应的生产检查间隔n 。
针对问题二:第二问中条件变为该工序正常时产出的零件不全是合格品,有2%为不合格品;而工序故障时产出的零件有40%为合格品,60%为不合格品且工序正常而误认有故障停机产生的损失费用为1500元/次。
所以第二问中计算效益函数L 时要考虑两种误判情况带来的损失,一是工序正常时检查到不合格品,误判停机将使检查的费用增加;二是工序故障时检查到合格品,将继续生产直到下一次检查,使不合格数量增多造成的损失。
效益函数L 的表达式因此有所改变,但建模方法基本与第一问相似。
针对问题三:在第二问情况下只定期检查一个零件造成了许多误判的情况,从而使每个零件的平均管理费用较高。
针对这种情况,我们采取适当连续检查多个零件降低误判率的方法达到减少每个零件的平均管理费用,是模型更优化。
4.数据分析刀具故障时加工的零件服从正态分布根据所给的100个样本数据用Excel 统计可得以下结果:表4.1 样本统计结果图4.1 样本分布直方图再利用6SQ统计软件进行卡方拟合优度检验得到如下结果:表5.问题一解答5.1 模型一的建立首先,在预防保全措施下,定义平均每一个零件的损失费用(效益函数)为L ,表达式为:123f c d k t LLLLanb⋅+=++=++(1)其中,1L 为预防保全费用, 2L 检查费用, 3L 为故障造成的不合格品损失和修 复费用。
b 为工序平均故障间隔,c 为相邻两次检查的后一次检查发现故障时,n 件零件中不合格品的平均数。
令在相邻两次检查的后一次发现故障的条件下,出现i 件不合格品的概率为:1(1)1(1)n i npppp--⋅=--则得 : 111(1)1(1)n ni i n i i i npppc p==--⋅=⋅=⋅--∑∑ (2)上式中1,2,3i n =⋅⋅⋅,上式经运算可得:21112()2122n n n pp co +-+=++≈ 由此得到c 与n 的函数关系,代入(1) 得:(1)2n fkt d Lanb+⋅=+++(3)然后给出的100 个数据分析算出无预防性更换时, 刀具故障平均间隔为μ=600 件,再根据题设刀具故障占95% , 非刀具故障占5% , 故非刀具平均故障间隔为95%5%mμ==11400件,其次由100 个数据确定刀具寿命的经验分布或拟合分布得密度函数:22()2(),0,xf x x x Zeμσ--=<<∞∈22()2001()()xx xF x f t dt dteμσ--⇒==⎰⎰为分布函数。
其中,600μ=,196.629σ=所以当进行预防保全定期n更换刀具时, 刀故障的平均间隔为:[]111()(1)[1()]()aaii F i F i a F aF aμ-=⎧⎫=⋅--+⋅-⎨⎬⎩⎭∑工序的平均故障间隔b由aμ和m决定, 满足111ab mμ=+即:111abmμ=+由此得到b和a之间的函数关系。
5.2模型一的求解对目标函数(3) 的参数进行如下优化:1.给定a,计算出b,代入(3)可得知L是n的函数,易得当n=时目标函数L达到极小;2. 按一定的步长取a的值, 采取逐渐缩小范围并逐个求出L的极小值及相应的n值, 其中使L最小者所对应的a和n即为所求。
本步骤我们在MATLAB软件中计算(对应程序段见附录2)得到的结果如下:min 5.297L=元,此时对应的342a=件,16n=件图5.1 a取值与L的变化关系图5.3结果分析:通过逐步求解,我们得到当定期换刀间隔为342件,定期检查间隔为16件时,使得生产每个零件的平均管理成本(平均损失费用)L达到极小值5.297元。
由a取值与L的变化关系图我们发现,当步长a的取值小于或大于342件时均会使平均损失费用L增大。
6.问题二的解答6.1确立新目标函数关系,令a sn第二问的效益函数要考虑两种误判。
一是工序正常时检查到不合格品误判停机, 将使损失的费用增加;二是工序故障时检查到合格品, 将继续生产直到下一次检查, 使不合格品数量增加,此时两次故障间由此产生的不合格品平均数为:[211(1)(1)(1)1(1)]1(1)12112js j i j njn i i an ppqqqun pqn nq==⎧⎫----⎪⎪⎪⎪-=+⋅⋅-⎨⎬--⎪⎪⎪⎪⎩⎭≈++∑∑+-上式中40%q= 为工序故障时的合格品率,p 为工序在生产一零件时的平均故障率,故在第该问的条件下, 效益函数L 应为:2(1)1n fk d pp t eLa nb bμ⎡⎤=++-⋅+⋅+⎢⎥⎣⎦' (4) 上式中2%p ='是工序正常时零件的不合格品率,1500e =元为第一种误判产生停机的损失费。
6.2问题二的求解计算再应用与问题一相同的模型代入式(4)并用MATLAB 软件求解(对应程序段件附录3)可得以下结果:min 7.381L =元,此时对应的 299a =件,18n =件图6.1 a取值与L的变化关系图6.3结果分析:在第二问的条件下运用和第一问相同的模型逐步求解,我们得到当定期换刀间隔为299件,定期检查间隔为18件时,使得生产每个零件的平均管理成本(平均损失费用)L达到极小值7.381元。
再由a取值与L的变化关系图我们发现,当步长a的取值小于或大于299件时均会使平均损失费用L增大。
7.问题三的解答7.1模型二的建立由于在第二问情况下生产出的零件不完全是合格品或是不合格品,只定期检查一个零件时,不免会出现许多误判,造成不必要的损失.。
今改进检查方式,采取适当连续检查多个零件降低误判率,尽量避免这样的损失,将获得更高的效益。
具体方法如下:①假设工序发生了故障:(表中“1”表示检测到合格品,“0”表示检查到不合格品)7.2结论及分析在进行检查时,不能由一次检查结果妄下结论,这可能因误判造成大的损失。
由以上模型可以得出:在工序发生故障时误判率为0.208,比检查一次的误判率0.4减少0.192;在工序正常时误判率为0.000792,比检查一次的误判率0.02减少0.019208。
因为在工序故障时误判引起的损失为200元/件,工序正常时因误判停机造成的损失为1500/次,这远远大于检查费用10元/次。