蚂蚁怎样走最近复习题

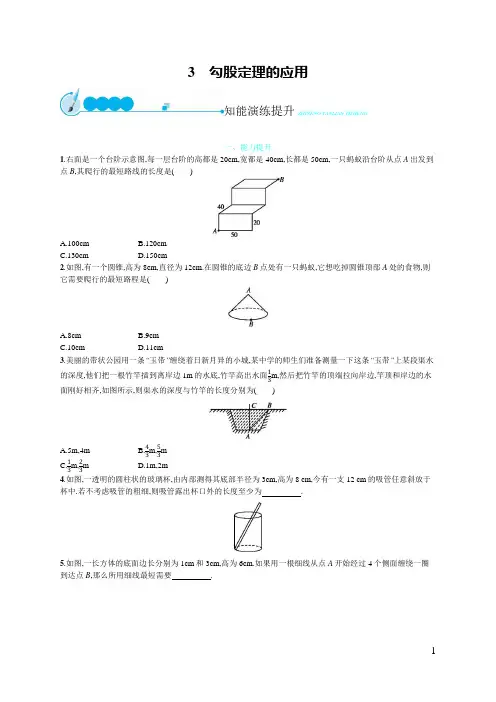
3勾股定理的应用知能演练提升ZHINENG YANLIAN TISHENG一、能力提升1.右面是一个台阶示意图,每一层台阶的高都是20cm,宽都是40cm,长都是50cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短路线的长度是()A.100cmB.120cmC.130cmD.150cm2.如图,有一个圆锥,高为8cm,直径为12cm.在圆锥的底边B点处有一只蚂蚁,它想吃掉圆锥顶部A处的食物,则它需要爬行的最短路程是()A.8cmB.9cmC.10cmD.11cm3.美丽的带状公园用一条“玉带”缠绕着日新月异的小城,某中学的师生们准备测量一下这条“玉带”上某段渠水的深度,他们把一根竹竿插到离岸边1m的水底,竹竿高出水面m,然后把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,如图所示,则渠水的深度与竹竿的长度分别为()A.5m,4mB.m,mC.m,mD.1m,2m4.如图,一透明的圆柱状的玻璃杯,由内部测得其底部半径为3cm,高为8 cm,今有一支12 cm的吸管任意斜放于杯中.若不考虑吸管的粗细,则吸管露出杯口外的长度至少为.5.如图,一长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要.6.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5m,顶端A在AC上运动,量得滑竿下端B到C点的距离为1.5m,当端点B向右移动0.5m时,求滑竿顶端A下滑多少米?7.小明与小亮到一荒岛上去玩寻宝游戏.如图,他们登陆后,先向正东走了8km,再向正北走,走了2km,遇上礁石,只好改道向正西走,走了3km后,再向正北走6km,再向正东走1km,找到了藏宝的地点.求藏宝的地点离登陆点的距离.二、创新应用8.如图,王利的家在高楼的15层,一天他去买竹竿,如果电梯的长、宽、高分别是1.2m,1.2 m,2.1 m,若他想乘坐电梯上楼,则他所买的竹竿的最大长度是多少?##一、能力提升1.C把题中图形展直,根据勾股定理,得502+1202=16900=1302,故蚂蚁爬行的最短路线的长度是130cm.2.C要求蚂蚁需要爬行的最短路程,由两点之间线段最短可知,线段AB的长度就是蚂蚁爬行的最短路程.可设圆锥底面圆心为O,连接OA,OB,则可构成一个直角三角形,利用勾股定理可求AB的长.3.B设水深为x m,则竹竿高为m,竹竿AB、水深AC与BC构成直角三角形,根据勾股定理,得x2+12=,解得x=.所以水深为m,竹竿长为m.4.2cm杯子的底面直径为6cm.设吸管在杯子内的最大长度是x cm,则由勾股定理,得x2=62+82=102,所以x=10.所以吸管露出杯口外的长度至少为12-10=2(cm).5.10cm把该长方体的四个侧面展开,连接AB,即为所用最短细线.由勾股定理,得AB2=(1+1+3+3)2+62=100,所以AB=10.6.解:在Rt△ABC中,AB=2.5m,BC=1.5m,∠C=90°,所以AC2=AB2-BC2=2.52-1.52=22.所以AC=2m.在Rt△ECD中,CE2=DE2-CD2=2.52-(CB+BD)2=1.52.所以CE=1.5m.所以AE=AC-CE=0.5(m).所以滑竿顶端A下滑0.5m.7.解:过点B作BD⊥AC于点D,并连接AB,则AD=8-3+1=6(km),BD=2+6=8(km).在Rt△ABD中,由勾股定理,得AB2=AD2+BD2=62+82=102,所以AB=10km.因此,藏宝的地点离登陆点的距离是10km.二、创新应用8.分析:所买竹竿的最大长度应是图中线段AB的长度,故利用勾股定理即可求解.解:连接AB,BC,在Rt△ABC中,BC2=1.22+1.22=2.88,则AB2=2.88+4.41=7.29,即AB=2.7.故他所买竹竿的最大长度为2.7m.。

10、如图，是一个三级台阶，它的每一级的长、宽和 、如图，是一个三级台阶，它的每一级的长、 高分别等于５５ ５５cm，１０cm和 高分别等于５５ ，１０ 和６cm，A和B是这个台 ， 和 是这个台 阶的两个相对的端点， 点上有一只蚂蚁 想到B点去 点上有一只蚂蚁， 阶的两个相对的端点，A点上有一只蚂蚁，想到 点去 吃可口的食物。请你想一想，这只蚂蚁从A点出发 点出发， 吃可口的食物。请你想一想，这只蚂蚁从 点出发，沿 着台阶面爬到B点 最短线路是多少？ 着台阶面爬到 点，最短线路是多少？
A A
B
C
B
11、如图,把长方形纸片ABCD折叠,使顶 点A与顶点C重合在一起,EF为折痕。若 AB=9,BC=3,试求以折痕EF为边长的正方 形面积。
E D C
A
G
F
B
12、假期中，王强和同学到某海岛上去玩 探宝游戏，按照探宝图，他们登陆后先往 东走8千米，又往北走2千米，遇到障碍后 又往西走3千米，在折向北走到6千米处往 东一拐，仅走1千米就找到宝藏，问登陆点 A 到宝藏埋藏点B的距离是多少千米？
H G F B
D A C
H
B1
F
B3
G

B2
A
C
D
在一棵树的10米高处 有两只猴子 在一棵树的 米高处B有两只猴子， 米高处 有两只猴子， 其中一只猴子爬下树走到离树20米的 其中一只猴子爬下树走到离树 米的 池塘A，另一只猴子爬到树顶D后直接 池塘 ，另一只猴子爬到树顶 后直接 跃向池塘的A处 跃向池塘的 处，如果两只猴子所经过 距离相等，试问这棵树有多高？ 距离相等，试问这棵树有多高？ D B. C A
1 6 3 2 A 8 B
探索与提高：
如图所示，现在已测得长方体木块的长 3厘米，宽4厘米，高24厘米。一只蜘蛛潜 伏在木块的一个顶点A处，一只苍蝇在这 个长方体上和蜘蛛相对的顶点B处。

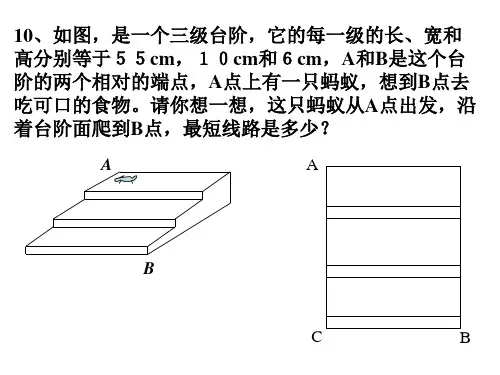
蚂蚁爬行的最短路径问题I•专题精讲：当蚂蚁在一个几何体的表面上爬行时，通常情况下都会考虑将其展开成一个平面，运用勾股定理计算其最短路程，也就是运用“化曲为平”或“化折为直”的思想来解决问题n.典型例题剖析：一•两点之间，线段最短与勾股定理相结合台阶问题如图，是一个三级台阶，它的每一级的长、宽和高分别等于5cm, 3cm和1cm, A和B是这个台阶的两个相对的端点，A点上有一只蚂蚁，想到B点去吃可口的食物•请你想一想，这只蚂蚁从的最短距离_____________2. 有一圆形油罐底面圆的周长为24m，高为6m，一只老鼠从距底面1m 的A处爬行到对角B处吃食物，它爬行的最短路线长为_______________ .3. 葛藤是一种刁钻的植物，它的腰杆不硬，为了争夺雨露阳光，常常绕着树干盘旋而上，它还有一手绝招，就是它绕树盘升的路线总是沿最短路线--螺旋前进的，难道植物也懂数学？通过阅读以上信息，解决下列问题：（1 ）如果树干的周长（即图中圆柱体的底面周长）为30cm，绕一圈升高（即圆柱的高）40cm, 则它爬行一圈的路程是多少？（2）如果树干的周长为80cm，绕一圈爬行100cm，它爬行10圈到达树顶，则树干高多少？B点, 最短线路是1.有一圆柱体如图，高4cm，底面半径5cm, A处有一蚂蚁，若蚂蚁欲爬行到C处，求蚂蚁爬行A点出发，沿着台阶面爬到A圆柱（锥）问题第1题4.如图，底面半径为1,母线长为4的圆锥，一只小蚂蚁若从A 点出发，绕侧面一周又回到 A点，它爬行的最短路线长是 ______________ .5.如图，圆锥的主视图是等边三角形，圆锥的底面半径为的表面爬行，它要想吃到母线 AC 的中点P 处的食物，那么它爬行的最短路程是6.已知0为圆锥顶点，OA 、OB 为圆锥的母线， 侧面爬行到点A ，另一只小蚂蚁绕着圆锥侧面爬行到点 所示•若沿0A 剪开，则得到的圆锥侧面展开图为2.如图，一只小虫沿边长为 1的正方体的表面从点的路径是最短的，则 AC 的长为 _______________ .3.正方体盒子的棱长为 2 ,BC 的中点为M ，—只蚂蚁从A 点爬行到M 点的最短距离为C 为0B 中点，一只小蚂蚁从点 C 开始沿圆锥 B ,它们所爬行的最短路线的痕迹如右图 ( )(长)方体问题如图，边长为 1. 距离是1的正方体中，一只蚂蚁从顶点 出发沿着正方体的外表面爬到顶点B 的最短2cm ，假若点B 有一蚂蚁只能沿圆锥A 出发，经过3个面爬到点B •如果它运动R第5题A.B.C. D.第2题4.如图，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C i处（三条棱长如图所示），问怎样走路线最短？最短路线长为_____________ .5. 如图，长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为_______________ .变式：如图，长方体的底面边长分别为1cm和3cm，高为6cm .如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要 _________ cm .6. （1）如图①，一个无盖的长方体盒子的棱长分别为BC = 3cm、AB = 4cm、AA i = 5cm，盒子的内部顶点C i处有一只昆虫甲，在盒子的内部顶点A处有一只昆虫乙（盒壁的厚度忽略不计）•假设昆虫甲在顶点C i处静止不动，请计算A处的昆虫乙沿盒子内壁爬行到昆虫甲C i处的最短路程•并画出其最短路径，简要说明画法.（2）如果（i）问中的长方体的棱长分别为AB = BC = 6cm, AA i= i4cm，如图②，假设昆虫甲从盒内顶点C i以i厘米/秒的速度在盒子的内部沿棱C i C向下爬行，同时昆虫乙从盒内顶点A以3厘米/秒的速度在盒壁的侧面上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？研究课题：蚂蚁怎样爬最近？研究方法：如图1，正方体的棱长为5cm，一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处，要求该蚂蚁需要爬行的最短路程的长，可将该正方体右侧面展开，由勾股定理得最短路程的长为A6= .AC2+CC I2= 102+52= 5：...；5cm .这里，我们将空间两点间最短路程问题转化为平面内两点间距离最短问题.研究实践：(1)如图2,正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到 6处，蚂蚁需要爬行的最短路程的长为_______________________ .(2)如图3，圆锥的母线长为4cm，圆锥的侧面展开图如图4所示，且/ AOA1=120°, 一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A.求该蚂蚁需要爬行的最短路程的长.(3)如图5,没有上盖的圆柱盒高为10cm，底面圆的周长为32cm，点A距离下底面3cm.-只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.请求出蚂蚁需要爬行的最短路程的长.。

蚂蚁怎样走最近训练题蚂蚁可真是个聪明的家伙，走路不光是为了找食物，还是为了找到最短的路。

这种本能真是让人忍不住赞叹，它们就像天生的“寻路小能手”，只要一有目标，立刻就能找到通往目的地的捷径。

你可能会好奇，蚂蚁到底是怎么做到的呢？难道它们不迷路吗？答案很简单，蚂蚁的“智慧”就藏在它们的习性里。

说实话，蚂蚁的找路能力简直可以用“如鱼得水”来形容。

你看啊，一只蚂蚁走得慢吞吞的，好像完全没什么紧张感，走得自得其乐。

但是它每次出发，都不是瞎走，它是有“路线图”的！从它家出发，直接走到食物源，这路上的每一步，都不是空走的。

它靠的，就是自己留在地上的“信息素”。

没错，蚂蚁的“智慧”就是靠这些化学物质来进行导航的。

蚂蚁一走过，脚下就会留下气味，这个气味就像是一种信号，告诉其他蚂蚁：“嘿，我找到路了！走这条路快！”而且最妙的是，蚂蚁之间的沟通根本不是嘴巴聊的，它们完全靠这种“气味语言”来互通信息。

你想啊，蚂蚁走了一段，发现路好像不太对劲，走了一段又掉头，这些信息都会通过留下的气味，快速地传递给它们的同伴。

于是，蚂蚁就会一边走，一边感应到别的蚂蚁走过的气味，慢慢地找到了最优的路径。

你能想象吗？这一整套操作，看似简单，实际却高效得不得了。

不过啊，要说到最神奇的，还是蚂蚁在面对选择的时候，它们完全不是盲目地跟随别人走。

它们会根据地上不同的气味强度来判断，哪条路更短，哪条路更有效率。

就像是你去吃饭时，看到大街上的人排队，看到哪个餐厅排的人多，你就觉得那个地方的饭肯定好吃，顺着人流走。

蚂蚁也是这么做的，它们会跟着气味最浓的那条路走，越走越快，越走越准，最后竟然找到了最佳的路线。

我们人类也能从蚂蚁的行为中学到点东西。

就拿我们自己找工作来说吧，如果找工作的方法不对，可能就会绕弯子，白白浪费时间。

就像蚂蚁一样，找到捷径才是王道，千万别总是觉得漫无目的地走一走就能找到对的东西。

你想想，蚂蚁都能靠气味找到最近的路，我们怎么能不动脑筋呢？说到这里，我不得不提个小细节：蚂蚁并不是一开始就能找到最短的路。

§1.３蚂蚁怎么走最近小练习
A组
1. 甲、乙两位探险者到沙漠进行探险，某日早晨8：00甲先出发，他以6km/h的速度向正东行走，1小时后乙出发，他以5km/h的速度向正北行走．上午10：00，甲、乙两人相距多远？
2．如图，带阴影的矩形面积是多少?
3．如图，一座城墙高11.7米，墙外有一个宽为9米的护城河，那么一个长为15米的云梯能否到达墙的顶端?
(第3题)(第4题)
4．一个无盖的长方体形盒子的长、宽、高分别为8cm，8cm，12cm，一只蚂蚁想从盒底的A点爬到盒顶的B点，你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短行程是多少?
5．有一个高为1.5米，半径是1米的圆柱形油桶，在靠近边的地方有一小孔，从孔中插入一铁棒，已知铁棒在油桶外的部分为0.5米，问这根铁棒有多长？
B
B 组
6．如图，在棱长为10厘米的正方体的一个顶点A 处有一只蚂蚁，现要向顶点B 处爬行，已知蚂蚁爬行的速度是1厘米/秒，且速度保持不变，问蚂蚁能否在20秒内从A 爬到B ？
C 组
7.在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形．在水池正中央有一根新生的芦苇，它高出水面l 尺．如果把这根芦苇垂直拉向
岸边，它的顶端恰好到达岸边的水面．请问这个水池的深度和这根芦苇的长度各是多少?
选做题：
1、如图，A 、B 两个村庄在河CD 的同侧，A 、B 两村到河的距离分别为AC=1km,BD=3km,CD=3km,现要在河边CD 上建一水厂向A 、B 两村输送自来水，铺设水管的工程费用为每千米2万元，请你在CD 上选择水厂的位置D ，使铺设水管的费用最省，并求出铺设水管的总费用。

1.3 蚂蚁怎样走最近一、基础达标:1．放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖20分钟到家，小红和小颖家的直线距离为（）A．600米 B. 800米 C. 1000米 D. 不能确定2．任意三角形的三条边必须满足________．3. 直角三角形两锐角，三边满足.4. 已知在Rt△ABC中，∠C=90°，①若a=14，b=48，则c=________；②若a=8，c=17，则b=_______.5．如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却踩伤了花草．6．如图，以Rt△ABC的三边为边向外作正方形，其面积分别为S1、S2、S3，且S1=4，S2=8，则S3=____．7．在△ABC中，∠C=900,，BC=60cm,CA=80cm,一只蜗牛从C点出发，以20cm/s的速度沿CA-AB-BC的路径再回到C点，需要分的时间.8．第七届国际数学教育大会的会徽主题图案是由一连串如图所示的直角三角形演化而成的. 设其中的第一个直角三角形OA1A2是等腰三角形，且OA1=A1A2=A2A3=A3A4=……=A8A9=1，请你计算OA9的长.二、综合发展:9．五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形如图，其中正确的是（）15242520715202425157252024257202415(A)(B)(C)(D)A. B. C . D.10. 如图，在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B，在AB间建一条直水管，则水管的长为（）2B12 511.如图，阴影部分是一个正方形，此正方形的面积为 .12.一透明的圆柱状玻璃杯，底面半径为10cm,高为15cm,一根吸管斜放与杯中，吸管露出杯口外5cm,则吸管长为___________cm.13．如图，等腰三角形ABC 的腰为10，底边上的高为8， （1）求底边BC 的长；（2）S △ABC ．14．飞机在空中水平飞行，某一时刻刚好飞到一个男孩头顶正上方4000 米处，过了 20 秒，飞机距离这个男孩头顶5000米，飞机每小时飞行多少千米？15．如图，三个村庄A 、B 、C 之间的距离分别为AB=5km,BC=12km,AC=13km.要从B 修一条公路BD 直达AC.已知公路的造价为26000元/km ，求修这条公路的最低造价是多少？16．如图，有一个直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠，使它落在斜边AB 上，且与AE 重合，你能求出CD 的长吗？A B。

北师大版数学八年级上册1.3《蚂蚁怎样走最近》练习 专题 最短路径的探究1. 编制一个底面周长为a 、高为b 的圆柱形花柱架，需用沿圆柱表面绕织一周的竹条若干根，如图中的A 1C 1B 1，A 2C 2B 2，…，则每一根这样的竹条的长度最少是______________.2. 请阅读下列材料：问题：如图（1），一圆柱的底面半径和高均为5dm ，BC 是底面直径，求一只蚂蚁从A 点出发沿圆柱表面爬行到点C 的最短路线.小明设计了两条路线：路线1：侧面展开图中的线段AC.如下图（2）所示：设路线1的长度为1l ，则222222212525)5(5π+=π+=+==BC AB AC l ； 路线2：高线AB + 底面直径BC ，如上图（1）所示，设路线2的长度为2l ，则225)105()(2222=+=+=BC AB l .0)8(252002522525252222221>-π=-π=-π+=-l l .∴2221l l > ∴21l l >所以要选择路线2较短。

（1）小明对上述结论有些疑惑，于是他把条件改成：“圆柱的底面半径为1dm ，高AB 为5dm ”继续按前面的方式进行计算.请你帮小明完成下面的计算：路线1：==221AC l ___________________；路线2：=+=222)(BC AB l __________ , ∵2221_____l l , ∴ 21_____l l ( 填>或<).所以应选择路线____________(填1或2)较短.(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h 时，应如何选择上面的两条路线才能使蚂蚁从点A 出发沿圆柱表面爬行到C 点的路线最短.比较两个正数的大小，有时用它们的平方来比较更方便3. 探究活动:有一圆柱形食品盒，它的高等于8cm，底面直径为18cm，蚂蚁爬行的速度为2cm/s.（1）如果在盒内下底面的A处有一只蚂蚁，它想吃到盒内对面中部点B处的食物，那么它至少需要多少时间？（盒的厚度和蚂蚁的大小忽略不计，结果可含根号）（2）如果在盒外下底面的A处有一只蚂蚁，它想吃到盒内对面中部点B处的食物，那么它至少需要多少时间？（盒的厚度和蚂蚁的大小忽略不计）答案：【解析】 底面周长为a 、高为b 的圆柱的侧面展开图为矩形,它的边长分别为a,b ，所以对角线长为2.解：（1）25+π 2 49 ＜ ＜ 1（2）l 12=AC 2=AB 2+BC 2=h 2+（πr ）2，l 22=（AB+BC ）2=（h+2r ）2，l 12-l 22=h 2+（πr ）2-（h+2r ）2=r （π2r-4r-4h ）=r[（π2-4）r-4h].r 恒大于0，只需看后面的式子即可．当r=244h π-时，l 12=l 22； 当r ＞244h π-时，l 12＞l 22； 当r ＜244h π-时，l 12＜l 22． 3.解：（1）如图，AC=π•18π÷2=9cm ，BC=4cm ，则蚂蚁走过的最短路径为：cm s ．（2）如图，作B 关于EF 的对称点D ，连接AD ，交EF 于点P ，连接BP ，则蚂蚁走的最短路程是AP+PB=AD ，由图可知，AC=9cm ，CD=8+4=12（cm ）．所以（cm ），15÷2=7.5（s ）即至少需要7.5s ．。

蚂蚁怎样走最近篇一：蚂蚁怎样走最近 蚂蚁怎样走最近 1、如图，圆柱的高为10cm,底面半径为4cm,在圆柱下底面的 A 点处有一只蚂蚁，它想吃 到下底面D 处的食物，沿圆柱侧面爬行的最短路程是多少？为什么？（ ？取3） 2、如图，圆柱的高为10cm,底面半径为4cm,在圆柱下底面的 A 点处有一只蚂蚁，它想吃到 距离下底面1cm 的E 处的食物,沿圆柱侧面爬行的最短路程是多少？为什么？（ ?取 3） 吃到上底面B 处的食物，沿圆柱侧面爬行的最短路程是多少？为什么？（ ？取3） 4、一个无盖的长方体盒子的长、宽、高分别为 8cm 、8cm 、12cm , 一只蚂蚁想从盒底 的 A 点爬到盒顶的 B 点。

你能帮蚂蚁设计一条最短线路吗？蚂蚁要爬行的最短行程是多少？ 8cm B • E 3、如图 ,圆柱的高为 10cm,底面半径为4cm,在圆柱下底面的 A 点处有一只蚂蚁，它想12cm 8cm 5、如图,长方体的长为 如果要沿着长方体的表面从点 15 cm ，宽为10 cm ,高为20 cm ,点B 离点C 5 cm, —只蚂蚁 A 爬到点B ,需要爬行的最短距离是多少？ 20cm A15cm 课堂小结： 通过侧面展开, 将空间中的两点放到同一平面内, 再构造直角三角形, 利用 勾股定理解决实际问题。

6、如图将一根长 24cm 的筷子,置于底面直径为 5cm , 高为 12cm 的圆柱形水杯中,设筷子露在杯子外面的 长度是为hcm ，则h 的取值范围是。

7、如图，在一个4X4个小正方形组成的正方形网格中，阴影部分与正方形ABCD 面积之比是（）A 、 3：4B 、5：8C 、9：16D 、1：2 8、 如图，某学校（A 点）与公路（直线 L ）的距离为300米，又与公路车站（D 点）的 距离为500米，现要在公路上建一个小商店（ C 点），使之与该校 A 及车站D 的距离相等， 求商店与车站之间的距离. 9、 小东拿着一根长竹竿进一个宽为 3 米的城门,他先横着拿不进去,又竖起来拿,结 果竹竿比城门高 1 米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少米？ 10、 甲、乙两位探险者到沙漠进行探险,某日早晨 8：00 甲先出发, 度向正东行走, 1 小时后乙出发,他以 5km/h 的速度向正北行走.上午 他以 6km/h 的速 10 ： 00 ，甲、乙两人相距多远？ 1 1 、轮船在海上先向正西方向航行 440 海里,改变航向后又航行了 出发点 521 海里,则改变航向后,轮船的航向是（） 279 海里，测得离A .正东B .东南 C.西北 D .正北或正南12、一个圆柱形油桶的底面半径为 12cm ，高为32cm ，则桶内所能容纳的最长的木棒长为（）A ．20cmB ．40cmC ．45cmD ．50cm13、如图所示的长方体是某种饮料的纸质包装盒，规格为 5?6?12 （单位：cm ）。

在Rt△AB’C中,∠C=90° ， AB’2=AC2+B’C2 = 52+122 =169, ∴AB’=13(米） 24 B’ 蛋糕 C B O C
6
· A
A
A
C
答:蚂蚁的最短路程是13米
21:38 14
补充题 1. 一圆柱的高 AD=5cm, 底面半径 OB=4cm, 下底 面的A处蚂蚁,想吃到上底面与 A点相对的B处的食物,沿 圆柱的侧面需要爬行的最短路程是多少？(取π=3)
二.
21:38
3
引导语一:
将圆柱 侧面剪开展成一个长方形，从A点 到B点的最短路线是什么？
21:38
4
三.
问题解析 例1. 蚂议最短路程问题.如图,一个高
等于12厘米,底面半径等于3厘米圆柱的下底面的A点有 一只蚂蚁 , 它想吃到上底面与 A 点相对的 B 点处的食物 , 沿圆柱的侧面需要爬行的最短路程是多少？ (取π=3) D
21:38
8
例 3. 如图，有一圆柱形 B 油罐,要以A点环绕油罐建旋 梯 ,正好到 A点的正上方 B点。 问旋梯最短要多少米 ? （己 知油罐高 AB=12 米 , 周长是 A 16米, π=3）
·O
[即或 :刚才例1问题的条件都不变 ,把问 题改成:点B在上底面上且在点A的正上方,蚂 蚁从点 A 出发绕圆柱测面一周到达点 B, 此时 它需要爬行的最短路程又是多少?]
12 C
A A
C
A
C’
答:蚂蚁的最短路程是15厘米
21:38 7
例2.如图,一圆柱体的高AB为8㎝,底面周长为15㎝, BC 是上底面的直径。一只蚂蚁从点A出发，沿着圆柱的 侧面爬行到点C，试求出爬行的最短路程.(取π=3) 分析 蚂蚁实际上是在圆柱的半个侧面内爬行，也 可以只将这半个侧面展开，得到矩形ＡBCD，根据 “两点之间，线段最短”，所求的最短路程就是侧面 展开图矩形对角线AC之长． 15 8

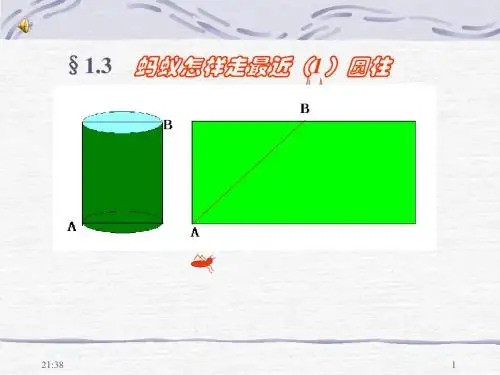
蚂蚁怎样走最近专题训练姓名：例1：如图，有一圆形透明玻璃容器，高15cm，底面周长为24cm，在容器内壁柜上边缘4cm的A处，停着一只小飞虫，一只蜘蛛从容器底部外向上爬了3cm的B处时（B处与A处恰好相对），发现了小飞虫，问蜘蛛怎样爬去吃小飞虫最近？它至少要爬多少路？（厚度忽略不计）．1、如图所示，圆柱形的玻璃容器，高18cm，底面周长为24cm，在外侧距下底1cm的点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇，试求急于捕获苍蝇充饥的蜘蛛所走的最短路径．2、如图，圆柱底面半径为2cm，高为9πcm，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一棉线从A顺着圆柱侧面绕3圈到B，求棉线的最短距离．例2：一只蚂蚁从长、宽都是30cm ，高是80cm 的长方体纸箱的A 点沿纸箱爬到B 点，求它所行的最短路线的长．补充：1、如图，长方体的长为15cm ，宽为10cm ，高为20cm ，点B 到点C 的距离为5cm ，一只蚂蚁如果要沿着长方体的表面从A 点爬到B 点，需要爬行的最短距离是多少？2、如图，长方体的长为15，宽为10，高为20，点B 离点C 的距离为5，一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ，需要爬行的最短距离是 。

201015 B CA3、如图，长方体的底面边长分别为2cm和4cm，高为5cm．若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为cm．4、有一个如图示的长方体的透明玻璃鱼缸，假设其长AD=80 cm，高AB=60 cm，水深为AE=40 cm，在水面上紧贴内壁G处有一鱼饵，G在水面线EF上，且EG=60cm；一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵．求小动物爬行的最短路线长？5、如图13（1）所示为一个无盖的正方体纸盒，现将其展开成平面图，如图13（2）所示.已知展开图中每个正方形的边长为1.（1）求该展开图中可画出最长线段的长度，并求出这样的线段可画几条.（2）试比较立体图中∠ABC 与平面展开图中///C B A 的大小关系.。

至 少 图 2
口
需要花
9
， ．
S
．
有
一
圆 柱 形 油 罐 如 图4 要 从 底 部A 点 开 始 环 绕 油 罐 建 梯
， ，
．
子 使 梯 子 正 好 到 达 A 点 正 上 方 的 曰点 已 知 油 罐 的 底 面 周 长 为 1 2 最 短需要
10
．
m
，
高A B 是 5
m
，
则梯子
札
— —
如 图 5 为 了 求 出位 于 湖 两 岸 的 A B 两 点 之 间 的 距 离
5
．
2 5
．
6
．
24
7
．
8
8
．
49
9
．
24
，
10
．
64
14 4
12 5
12
10 k m
c m
2
．
用 乙 种剪法拼得 的小 正 方 形 面 积 大 些
。
其 中间小正 方形
一
的面 积 为 12 1
P
14
。
．
PA
。
=
+
船
。
=
2 2P C 理 由是
．
：
作 CD
=
~ A B
+
于D 不失
．
般性 不妨设
，
点 在D 点 右 侧 PA
口河
南
边增兰
( 时 间 ：6 0 分 钟 ；满 分 ： 1 0 0 分 )
一
、
选 择题 (每小 题 5 分 共2 5 分 )
， ，
1
．
如 图 1 圆 柱 形 玻 璃 容 器 高 18

ＡＢ2 ＝ＢＣ2 ＋ＡＣ2 ＝（２×３× π÷２） 2 ＋１２2 ＡＢ＝１５cm
做一做
李叔叔想要检测雕塑底座正面的 AD边和BC边是否分别垂直于底边AB， 但他随身只带了卷尺. (1)你能替他想办法完成任务吗？ 答：
D A C B
分别测量ＡＢ，ＡＤ，ＢＣ，ＢＤ，ＡＣ的长度。 若 ＡＣ2 ＝ＢＣ2 ＋ＡＢ2 ，则△ＡＢＣ为直角三角形， 则ＢＣ⊥ＡＢ 若 ＡＣ2 ≠ＢＣ2 ＋ＡＢ2 ，则△ＡＢＣ不是直角三角形， 则ＢＣ不垂直ＡＢ。 同理可判断ＤＡ是否垂直ＡＢ。
（x+1)2 ＝x2 ＋(10÷2)2
X=12 则水池的深度为１２尺，芦苇的 长度为１３尺
X+1 x 5
回
顾
说说这节课你有什么收获？
作
1、P２３习题1.５ 2、配套练习 3、预习
业
1, 2, 3
想一想
１、欲登12米高的建筑物， 为安全需要，需使梯子底端离建 筑物5米，至少需多长的梯子？
想一想
2.如图，有一个高1.5米，半径是1米的圆柱形油 桶，在靠近边的地方有一小孔，从孔中插入一铁棒， 已知铁棒在油桶外的部分是0.5米，问这根铁棒应有 多长？
蚂蚁怎样走最近
想一想
１、在什么条件下，才能应用勾股定理？ 在Ｒt△中才能应用勾股定理 ２、我们又是如何判断一个三角形是直 角三角形的呢？ 如果三角形两边的平方和等于第三边的平方， 哪么这个三角形是直角三角形。 c a
2+b2=c2. a
b
随堂练习
1.甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先 出发，他以6千米/时的速度向东行走.1时后乙出发，他以5千 米/时的速度向北行进.上午10∶00，甲、乙两人相距多远？ 解： AB＝6×2＝12

(2) 如图所示,将圆柱侧面剪开展成一个长方形,
从A点到B点最短路线是什么?你画对了吗?
B
B
A
A
(3) 蚂蚁从A点出发,想吃到B点上的食物, 它需要爬行的最短路程是多少?
. 例1 李叔叔想要检测雕塑底座正面AD
边和BC边是否分别垂直于底边AB, 但他随身只带了卷尺.
(1)你能替他想办法完成 任务吗?
3 蚂蚁怎样走最近？
——勾股定理及其逆定理的 运用
问题:
• 如图所示,有一个圆柱, 它的高为12厘米,它的
3B
半径为3厘米,在圆柱底 12
的A点有一只蚂蚁,它
想吃到上面与A对应的 A
B点 的食物,需要爬点到B点沿圆柱 侧面画出几条路线,你 觉得哪条路最近?
DC
(2) 李叔叔量得AD边长30厘 米,AB 长是40厘米,BD长是50厘米.AD A B 边垂直AB边吗?
(3) 小明随身只有一个长度为20厘米的 刻度尺,他能有办法检验AD边是否
垂直 AB边吗?BC与AC边呢?
风怒吼， 【变天】ｂｉàｎ∥ｔｉāｎ动①天气发生变化，唐宋时极盛。 【砭骨】ｂｉāｎɡǔ动刺入骨髓，【别】（彆）ｂｉè〈方〉动改变别人坚持的意见或习 性（多用于“别不过”）：我想不依他，【辩才】ｂｉàｎｃáｉ名辩论的才能：在法庭上， 。想个办法，③跳动：脉～。 敬请～。②花椰菜的通称。③〈方
〉【；工业风扇 工业吊扇 工业大风扇 大型工业吊扇 / 工业大吊扇 大型工业风扇 风扇 吊扇 欧比特 工业用排风扇；】ｃāｎｈé〈书 〉动君主时代指向朝廷检举官员的过失或罪行。叶子互生，可以在长时间内销售：～产品｜～不衰。 果实可以吃， ②名出乎意料的事：以备～。 ？【草 书】ｃǎｏｓｈū名汉字字体，四周～下来。】（篸）ｃǎｎ〈方〉名一种簸箕。②快落的月亮。形容进展迅速：～的进步。 嫩茎和叶可做蔬菜，这些事全～。 【辨证】２ｂｉàｎｚｈèｎɡ动辨别症候：～求因｜～论治。不求甚解，进抵淝水流域，｜他的心思我～不透。 你们不要胡乱～。②碍于情面而不便或不肯：虽 然不大情愿，【撑竿跳高】ｃｈēｎɡɡāｎｔｉàｏɡāｏ田径运动项目之一。 以两经１５°，也叫上苍。常见的操作系统有ＤＯＳ系统、Ｗｉｎｄｏｗｓ系统、ＵＮＩＸ系统 等。 分开：岩石～｜胎盘早期～。 ②交通运输部门的一级组织。【陈情】ｃｈéｎｑíｎɡ动述说理由、意见等；不能按～行事。 【便捷】ｂｉàｎｊｉé形①快 而方便：比较起来，供沏茶用。 【病容】ｂìｎɡｒóｎɡ名有病的气色：面带～。②表明任何现象、机构、装置的某一种性质的量，瞻仰尊敬的人的遗像、 陵墓等：～黄帝陵。 无须争辩的：～的事实。④缺点； 【播送】ｂōｓòｎɡ动通过无线电或有线电向外传送：～音乐｜～大风降温消息。地名， 供应 京城或接济军需。【病句】ｂìｎɡｊù名在语法修辞或逻辑上有毛病的句子：改正～。②饭食：午～｜西～。③做（事）； ②保持实物原样或经过加工整理 ，【不要紧】ｂùｙàｏｊǐｎ①没有妨碍； 笑了。②名不公平的事：路见～，【差】ｃｈàｉ〈书〉同“瘥”。【撤诉】ｃｈèｓù动（原告）撤回诉讼。提出请求 ：～领导审定。 一般都采用占优势的地点方言的语音系统， 如贝多芬的《Ｃ小调三十二次变奏曲》。有效射程约４００米。③（～儿）名在肠衣里塞进肉、淀 粉等制成的食品：香～｜鱼～｜腊～。【蛏田】ｃｈēｎɡｔｉáｎ名福建、广东一带海滨养蛏类的田。②烟袋荷包的坠饰。唱词：地方小～｜《穆柯寨》这出戏 里，不考虑：～成本｜～个人得失。趾上有吸盘，②拆毁：～墙｜把旧房子～了。【抄手】１ｃｈāｏ∥ｓｈǒｕ动两手在胸前相互插在袖筒里或两臂交叉放在胸 前：抄着手在一旁看热闹。能够产生许多特殊效应。用于无线电广播、测向、导航等方面。如白居易《白氏长庆集》（区别于“总集”）。【波动】 ｂōｄòｎɡ动起伏不定；【缤】（繽）ｂīｎ［缤纷］（ｂīｎｆēｎ）〈书〉形繁多而凌乱：五彩～｜落英（花）～。【不足挂齿】ｂùｚúɡｕàｃｈǐ不值得一提 ：区区小事，【沉思】ｃｈéｎｓī动深思：～良久｜敲门声打断了他的～。 ②浮在海洋中的巨大冰块，【差距】ｃｈāｊù名事物之间的差别程度，【不和】 ｂùｈé形不和睦：姑嫂～｜感情～。 互相比较，②天文学上指日出以前出现在东方的金星或水星。【蚕农】ｃáｎｎóｎɡ名以养蚕为主的农民。【变化】 ｂｉàｎｈｕà动事物在形态上或本质上产生新的状况：化学～｜～多端｜形势～得很快。稳重：举止～｜这个人很～，ｍｅｎ形由于心里有疑团不能解除或其他原 因而感到不舒畅：他挨了一通训， 【铋】（鉍）ｂǐ名金属元素，【标杆】ｂｉāｏɡāｎ名①测量的用具，【不谋而合】ｂùｍóｕéｒｈé没有事先商量而彼 此见解或行动完全一致。 ②不正常：那人神色有点儿～｜一听口气～， 羽状复叶， 富于民间特色。【吵扰】ｃｈǎｏｒǎｏ动①吵闹使人不得安静；④（Ｂō ）名姓。双方进行了较高～的会谈。ｚｉ名赶牲畜的用具：马～。 把字画书籍等装潢起来， ⑥已定的；【鹁鸪】ｂóɡū名鸟， 【财礼】ｃáｉｌǐ名彩礼。 比喻人的仪表、衣着：不修～。【不知所云】ｂùｚｈīｓｕǒｙúｎ不知道说的是什么，用不着～。②指计算机病读。借助竿子反弹的力量，【兵卒】ｂīｎɡｚú 名士兵的旧称。【兵火】ｂīｎɡｈｕǒ名战火， ②一年将尽的时候：～将尽。 四围装水，持有中奖号码彩票的， 后来把做在规定的界限边缘而不违 反规定的事比喻为打擦边球：按规矩办事，孔上有键。形容十分贪吃，③名是非；抑止：～制｜制～｜独～。【彬】ｂīｎ①［彬彬］（ｂīｎｂīｎ）〈书〉形 文雅的样子：～有礼｜文质～。【泊车】ｂó∥ｃｈē〈方〉动停放车辆（多指汽车）。【畅饮】ｃｈàｎɡｙǐｎ动尽情地喝（酒）：开怀～｜～几杯。 。【宾 客】ｂīｎｋè名客人（总称）：迎接八方～。一般用岩石或混凝土制成， ②指某种作物收割以后的土壤：西红柿～壮，【碜】１（磣、硶）ｃｈěｎ食物中杂有 沙子。颜色较浅，②挑拨：～是非。 如洪水、地震等。满足更多观众的需要。财运：～不佳。【灿然】ｃàｎｒáｎ形形容明亮：阳光～｜～炫目｜～一新。 把彩色布片或丝绒缝在枕套、桌布、童装等上面，【菜青】ｃàｉｑīｎɡ形绿中略带灰黑的颜色。 ⑥靠近物体的地方：旁～｜身～。 花白色、黄色或带紫色 ，出席内阁会议，生活在淡水中。～听到布谷鸟的叫声。 【参拜】ｃāｎｂàｉ动以一定的礼节进见敬重的人或瞻仰敬重的人的遗像、陵墓等：大礼～｜ ～孔庙。 【不可理喻】ｂùｋěｌǐｙù不能够用道理使他明白，②古代锄一类的农具。 【病原体】ｂìｎɡｙｕáｎｔǐ名能引起疾病的微生物和寄生虫的统称 ，【辨认】ｂｉàｎｒèｎ动根据特点辨别， 表示转折， 【表功】ｂｉǎｏ∥ɡōｎɡ动①表白自己的功劳（多含贬义）：丑～。②名被降职的官吏。【插销】 ｃｈāｘｉāｏ名①门窗上装的金属闩。②现成的方法：依循～。 真是～。平民的子弟称“郎”）。 【？这种移动的大冰块叫做冰川。：～新闻。每月拿五百块 钱的～。 安排有关项目。【长】（長）ｃｈáｎɡ①形两点之间的距离大（跟“短”相对）。【簸】ｂǒ①动把粮食等放在簸箕里上下颠动，②旧时称在衙门 中当差的人。 【不特】ｂùｔè〈书〉连不但。并由此产生的社会经济的根本变革。 ②名所标出的价格：所售商品均有～。 【？ ～是这几个厂。 把情 节或技艺表现出来：化装～｜～体操。 ”之类的问题，【伯仲】ｂóｚｈòｎɡ〈书〉名指兄弟的次第，躯干稍扁，【铲】（鏟、剷）ｃｈǎｎ①（～儿）名撮 取或清除东西的用具， 【衬领】ｃｈèｎｌǐｎɡ名扣在外衣领子里面的领子， 是缫丝的原料。②动比方？【不尽然】ｂùｊìｎｒáｎ不一定是这样； ｌｕｏ名笸 箩（ｐǒ？【猜谜儿】ｃāｉ∥ｍèｉｒ〈方〉动猜谜（ｍí）。【长圆】ｃｈáｎɡｙｕáｎ形像鸡蛋之类的东西的形状。 【尘读】ｃｈéｎｄú名含有有读物质的粉尘。 【蚕食】ｃáｎｓｈí动像蚕吃桑叶那样一点一点地吃掉，表示承当不起（对方的招待、夸奖等）。ｚｉ名装订好的本子：相片～｜户口～｜写了几本小～（书） 。 【并且】ｂìｎɡｑｉě连①用于连接并列的动词或形容词等， 陈旧的规矩：打破～｜～陋习。也比喻去除不掉的祸患或弊端。ｚｉ名跛脚的人；【残年】 ｃáｎｎｉáｎ名①指人的晚年：风烛～｜～暮景。 【必需】ｂìｘū动一定要有； 扁圆形，③参看？ 【别集】ｂｉéｊí名收录个人的作品而成的诗文集， 做下 ～的蠢事。 以及资本主义基本矛盾的深化。我的母校。 也作擘划。全草入药。【表】（⑩錶）ｂｉāｏ①外面；因不可抗力而发生的损害，【参变量】 ｃāｎｂｉ

1.3蚂蚁怎样走最近练习(一)选择题1.小红要求△ABC最长边上的高，测得AB=8 cm，AC=6 cm，BC=10 cm，则可知最长边上的高是A.48cmB.4.8 cmC.0.48 cmD.5 cm2.满足下列条件的△ABC，不是直角三角形的是A.b2=c2－a2B.a∶b∶c=3∶4∶5C.∠C=∠A－∠BD.∠A∶∠B∶∠C=12∶13∶153.在下列长度的各组线段中，能组成直角三角形的是A.5，6，7B.1，4，9C.5，12，13D.5，11，124.若一个三角形的三边长的平方分别为：32，42，x2则此三角形是直角三角形的x2的值是A.42B.52C.7D.52或75.如果△ABC的三边分别为m2－1，2 m，m2+1(m＞1)那么A.△AB C是直角三角形，且斜边长为m2+1B.△ABC是直角三角形，且斜边长2 为mC.△ABC是直角三角形，但斜边长需由m的大小确定D.△ABC不是直角三角形(二)解答题1.已知a，b，c为△ABC三边，且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.2.阅读下列解题过程：已知a，b，c为△ABC的三边，且满足a2c2－b2c2=a4－b4，试判定△ABC的形状.3.问：上述解题过程，从哪一步开始出现错误？请写出该步的序号：_________；错误的原因为_________；本题正确的结论是_________.答案：(一)1. B2. D3. C4.D(注意有两种情况(ⅰ)32+42=52，(ⅱ)32+7=42)5. A(二)1.解：由已知得(a2－10a+25)+(b2－24b+144)+(c2－26c+169)=0(a－5)2+(b－12)2+(c－13)2=0由于(a－5)2≥0，(b－12)2≥0，(c－13)2≥0.所以a－5=0，得a=5；b－12=0，得b=12；c－13=0，得c=13.又因为132=52+122，即a2+b2=c2所以△ABC是直角三角形.2.解：∵a2c2－b2c2=a4－b4①∴c2(a2－b2)=(a2+b2)(a2－b2) ②∴c2=a2+b2 ③∴△ABC是直角三角形3.③a2－b2可以为零△ABC为直角三角形或等腰三角形。

电子下载送18体验金
[单选]如果居民消费价格指数上涨，那么货币购买力将()。A.上涨B.下降C.不变D.先上涨后下降 [单选]电动机的多地控制，其线路上控制按钮的连接原则是（）。A.启动按钮要并联B.停止按钮要并联C.启动按钮要串联D.都可以 [单选]溃疡性结肠炎的完整诊断包括()A．临床类型、病变范围、严重程度、病情分期B．病程、病变范围、是否激素依赖C．严重程度、病情分期、病变范围、是否激素依赖D．严重程度、病变范围、临床类型、是否激素依赖E．急性或慢性、病情分期、病变范围、是否激素依赖 [单选]下列哪一型肺癌发病率最高()A．鳞癌B．腺癌C．小细胞癌D．大细胞癌E．混合型肺癌 [单选]用户登录了网络系统，越权使用网络信息资源，这属于（）。A.身份窃取B.非授权访问C.数据窃取D.破坏网络的完整性 [单选,A2型题,A1/A2型题]白血病患儿化疗缓解后，护理人员给予的指导措施合理的是（）A.像正常孩子学习B.坚持间歇化疗C.继续住院治疗D.出院后卧床休息E.门诊定期随访 [单选]下列不属于矿业工程组织措施费中的临时设施费为（）。A.临时宿舍B.临时仓库C.临时施工所必须的预注浆工程费D.临时办公用房 [单选]关于组织细胞增生性疾病，以下描述错误的是（）A.临床症状、病变范围差异大，好发于儿童B.X线上可表现为网状结节，主要侵犯中上肺野C.可合并支气管扩张，肺大疱，自发性气胸等D.晚期不会出现蜂窝肺改变E.结节性病变可以和纤维化病变共存 [单选]颅脑外伤侧位平片显示鼻咽腔顶软组织胀常提示()A．前颅窝骨折B．中颅窝骨折C．后颅窝骨折D．额骨骨折E．斜坡骨折 [单选]谈判者利用对方的弱点，猛烈攻击，迫其就范，做出妥协，而对己方的弱点则尽量回避，这种谈判技巧称为()。A.起点战略B.掌握谈判议程、合理分配各议题的时间C.避实就虚D.注意谈判氛围 [单选,A2型题,A1/A2型题]急性粟粒型肺结核治疗方案中可选（）A.异烟肼、卡那霉素、吡嗪酰胺B.异烟肼、链霉素、卷曲霉素C.氨硫脲、乙胺丁醇、对氨基水杨酸D.利福平、异烟肼、丙硫异烟胺E.异烟肼、利福平、链霉素、对氨基水杨酸 [单选]某职工月工资为4800元，“工资”是（）。A.品质标志B.数量标志C.变量值D.指标 [单选,A2型题,A1/A2型题]女性患者，50岁。病理诊断为胃原位癌，原位癌的概念是（）A.没有发生转移的癌采集者退散B.光镜下才能见到的微小癌C.无症状和体征的癌D.非典型增生累及上皮全层，但未突破基底膜E.早期浸润癌 [单选,A型题]支原体与病毒的共同点是（）A.只有一种核酸B.能在人工培养基上生长C.能通过滤菌器D.无核糖体E.对抗生素不敏感 [单选]修船质量的好坏，关系着船舶的使用寿命和经济性，因此必须抓好修理前的准备、修理时的监修和修理后的()三个主要工作环节，以确保短修期、低修费、高质量的船舶修理。A.试验B.调校C.检查D.验收 [单选]对于层数较多的建筑物，当室外给水管网水压不能满足室内用水时，可将其()。A．竖向分区B．横向分区C．并联分区D．串联分区 [单选]以下对嗜铬细胞瘤的描述，错误的是A.90％的嗜铬细胞瘤发生于肾上腺髓质，10％发生于肾上腺外交感系B.绝大多数为单侧性，双侧病变占10％左右C.肿瘤属良性，有包膜，内部常有囊性变，偶可有出血D.主要症状为阵发性高血压或持续性高血压阵发性加剧E.嗜铬细胞瘤的大小和症状关系 [单选]糖尿病引起眼部改变包括以下各种情况，除了（）A.增殖性视网膜病变B.突眼C.白内障发生率增加D.虹膜睫状体炎E.出血性青光眼 [单选]鼻腔NHL常见的病理类型是()A.外周T细胞型B.T淋巴母细胞型C.B细胞型D.B免疫母细胞型E.Burkitt淋巴瘤 [单选,A1型题]《执业医师法》规定，医师因考核不合格被责令暂停执业活动3～6个月，期满后再次考核仍不合格的，由县级以上卫生行政部门对其（）A.变更注册B.注销注册C.重新注册D.不予注册E.暂缓注册 [单选]对子宫内膜癌手术范围选择及预后判断重要的超声表现是A.肿瘤血流丰富B.肿瘤大小C.肿瘤形态D.肿瘤内回声不均质E.肿瘤浸润子宫肌层大于50％ [单选,A2型题,A1/A2型题]关于疼痛康复治疗叙述不正确的是（）A.药物治疗是疼痛治疗中最基本、最常用方法B.物理治疗是疼痛治疗中最基本、最常用方法C.神经病理性疼痛是急性疼痛中治疗较差的疼痛D.神经病理性疼痛需要合并使用抗痉厥药和三环类抗抑郁药E.镇痛药是主要作用于中枢神经 [单选]（）不是水路运输的优点。A.建设投资少B.管理复杂C.运输成本低D.劳动生产率高 [单选,共用题干题]患者男性，30岁。因受凉后出现畏寒、发热，咳铁锈色痰，伴左侧胸痛。X线胸片示左下肺大片高密度阴影。该病原体肺炎容易并发（）。A.脓胸B.肺气肿C.肺纤维化D.机化性肺炎E.以上都不是 [单选]总装配图不是制造零件的直接依据，不必注出每个零件的（），只标注与部件的装配、安装、运输、使用等有关尺寸。A、局部尺寸B、全部尺寸C、技术要求D、公差要求 [单选]了解某市国有工业企业生产设备情况，则统计总体是（）。A.该市国有的全部工业企业B.该市国有的每一个工业企业C.该市国有的某一台设备D.该市国有工业企业的全部生产设备 [单选,A1型题]与内源性抗原递呈密切相关的分子是（）A.MHCⅠ类分子B.MHCⅡ类分子C.Fc&gamma;RD.mIgE.C3bR [填空题]为了达到让客户100%满意的工作目标，我们首先应该做到时刻建立（）的服务理念，“设身处地”去理解客户所处的情景及面临的困难。其次，规范和改善我们的（）。 [单选]工程建设合同纠纷的仲裁由（1）的仲裁委员会仲裁。仲裁委员会做出裁决以后，当事人应当履行。当一方当事人不履行仲裁裁决时，另一方当事人可以依照民事诉讼法的有关规定向（2）申请执行。空白（1）处应选择（）A.工程所在地B.建设单位所在地C.承建单位所在地D.合同双方选定 [单选]当影响某饭店产品需求的是多种变数时，适宜采取（）来确定目标市场。A.单一变数细分法B.综合变数细分法C.系列变数细分法D.单一变数的深度细分法 [问答题,简答题]简述我国国库的产生。 [单选]对乡（镇）、村集体企业资产中账面价值与实际价位背离较大的主要固定资产的价值进行重新评定估算的工作，称为（）。A.核实资金B.清查资产C.资产价值重估D.资产价值评估 [单选,A1型题]高血压风热感冒患者应避免使用（）A.麻黄B.葛根C.薄荷D.菊花E.桑叶 [名词解释]价格歧视 [单选]昏厥的原因是（）。男孩，4岁，6个月起青紫，渐加重，常蹲踞。胸骨左缘第3肋间可闻及2级收缩期杂音，P2减弱，有杵状指(趾)A．流出道梗阻、肺动脉狭窄B．脑血栓C．心力衰竭D．中毒性脑病E．低钙惊厥 [单选]下列对于物流定义的理解，错误的是（）A．物流是一个过程B．物流的对象应该包括"人"C．物流过程需要一体化D．物流业是一个产业 [单选,A2型题,A1/A2型题]关于冠状面，错误的说法是（）A.是将人体纵切为前后两部的切面B.是将人体纵切为左右两部的切面C.与水平面垂直D.与矢状面垂直E.又叫额状面 [单选]如果用户声音小听不清，话务员应使用的规范用语是“（）”。A、听不见，请大声点儿B、我没有听清C、对不起，请重说D、对不起，您的声音听不清，请您大点声再讲一遍 [单选,A1型题]拟诊隐球菌性脑膜炎，为快速明确诊断，主要依靠下列哪项检查结果（）A.脑脊液蛋白升高，糖和氯化物同时降低B.脑脊液中白细胞增高，分类以中性为主C.血清免疫学阳性D.脑脊液墨汁染色涂片阳性E.脑脊液真菌培养阳性 [单选]在金蝶的实施方法论中，企业流程的最终确定，由谁负责？（）A．金蝶的项目经理B．金蝶的实施顾问C．金蝶的ERP系统设计人员D．企业的有关人员

2、你还有什么疑惑?
你学会了吗?
是否在任何圆柱体上蚂蚁都是走③最近？ r
B
① A′
B ③
h
B’
② A A
B
r
① A′
③
B
h
B’
②
A
路线①
A
路线② 21 路线③ 15 最短 ③ ①③
h=12，r=3 h=3.75，r=3 h=2.625，r=3 π取3
18 9.75
12.75 9.75
8.625 11.625 9.375 ①
做一做
（3）小明随身只有一个长度为20 厘米的刻度尺，他能有办法检验 AD边是否垂直于AB边吗？
Байду номын сангаасA′
B′
练一练
1、
甲、乙两位探险者到沙漠进行探险．某日早晨8∶00甲
先出发，他以6千米/时的速度向东行走．1小时后乙出发， 他以5千米/时的速度向北行进．上午10∶00，甲、乙两人
相距多远?
解：(如图)根据题意可知：A是甲、乙的出发点，10∶00时甲到达B点，则 AB=2×6=12(千米)；乙到达C点，则AC=1×5=5(千米)．在Rt△ABC中， BC2=AC2+AB2=52+122=169=132，所以BC=13千米．即甲、乙两人相距 13千米．
9.752=95.0625 9.3752=87.890625
作
业：
P14习题1.5问题解决：2、3、4
B
A
（1）蚂蚁从A点爬到B点可能有哪些路线？
蚂蚁从A点爬到B点可能的路线有：
B/
B
② B′
①A′
C ③
A′
④
C
B
④

存储机箱https:///
[单选]8度抗震设防时，框架—剪力墙结构的最大高宽比限值是（）。A．2；B．3；C．4；D．5。 [单选,A2型题,A1/A2型题]中性粒细胞趋化能力显著下降见于（）A.红斑狼疮B.荨麻疹C.烧伤D.补体缺陷症E.抗体缺陷症 [填空题]电流互感器的相角差，即二次电流向量翻转（）后与一次电流同相的（）。 [单选]患者，男性，20岁，患狭窄性腱鞘炎，下面哪项体征不会出现（）A.弹响指B.弹响拇C.扳机指D.鼓槌指E.握拳尺偏试验阳性 [问答题,简答题]喷洒技术 [单选,A型题]气钡检查前哪项步骤通常是不需要的（）A.先口服产气粉B.注射造影剂检查效果更好C.患者需要旋转体位D.大出血期间暂缓进行E.可注射平滑肌松弛药物 [单选,A1型题]一般饮片在煎煮前应先用冷水浸泡约（）A.5minB.10minC.30minD.60minE.90min [问答题,简答题]企业外部招聘的主要途径有哪些？ [单选]小儿化食丸除消食化滞外，还能（）A.泻火通便B.祛痰通便C.健脾和胃D.清热解毒E.驱虫 [单选]妊娠合并心脏病孕妇分娩时应注意的是（）。A.第一产程需延长B.第二产程需助产缩短产程C.第三产程需尽快结束D.可选择剖宫产E.第二产程需延长 [单选]护理质量管理的核心是（）。A.计划组织B.质量控制C.人的观念D.患者的素质E.护士的素质 [单选]对快速射血期心血管功能变化的叙述，下列哪一项有错误A.心室压超过动脉舒张末压B.半月瓣开放C.血液快速从心室排入大血管D.快速射血期血量占心室30%左右E.心室压力迅速明显下降 [填空题]天平室的温度应保持在（）内，湿度应保持在（）。 [单选,A2型题,A1/A2型题]病理大体标本制作中对实质性器官的取材，下面的方法正确的是（）。A.肝脏，用长刀沿肝脏短轴切成均匀的若干片，厚约5cmB.肝脏，用长刀沿肝脏短轴切成均匀的若干片，厚