第三章牛顿运动定律的应用-传送带模型
- 格式:ppt
- 大小:483.00 KB
- 文档页数:24

【高三一轮教学案】牛顿运动定律应用--传送带模型2 017.10.1一、模型特征一个物体以速度v0(v0≥0)在另一个匀速运动的物体上开始运动的力学系统可看做“传送带”模型,如图(a)、(b)、(c) 所示。
①②③1.①擦力2.中S3.体速度变化再分析相对运动来判断以后的受力及运动状态的改变。
【名师点睛】1. 在确定研究对象并进行受力分析之后,首先判定摩擦力突变(含大小和方向)点,给运动分段。
传送带传送的物体所受的摩擦力,不论是其大小的突变,还是其方向的突变,都发生在物体的速度与传送带速度相等的时刻。
物体在传送带上运动时的极值问题,不论是极大值,还是极小值,也都发生在物体速度与传送带速度相等的时刻。
v物与v传相同的时刻是运动分段的关键点,也是解题的突破口。
2. 判定运动中的速度变化(即相对运动方向和对地速度变化)的关键是v物与v传的大小与方向,对二者的比较是决定解题方向的关键。
3.在倾斜传送带上需比较mg sin θ与F f的大小与方向,判断F f的突变情况。
4. 考虑传送带长度——判定临界之前是否滑出;物工件与传送带间的动摩擦因数μ=0.6,工件滑上A端时速度v A=10 m/s,设工件到达B端时的速度为v B。
(取g=10 m/s2)(1) 若传送带静止不动,求v B;(2) 若传送带顺时针转动,工件还能到达B端吗?若不能,说明理由;若能,求到达B点的速度v B;来源于网络来源于网络(3) 若传送带以v =13 m/s 逆时针匀速转动,求v B 及工件由A 到B 所用的时间。
【典例2】 如图所示,水平传送带A 、B 两端相距s =3.5 m ,物体与传送带间的动摩擦因数μ=0.1,物体滑上传送带A 端的瞬时速度v A =4 m/s ,到达B 端的瞬时速度设为v B .下列说法中正确的是( )A. 若传送带不动,v B = 3 m/sB. 若传送带逆时针匀速转动,v B 一定等于3 m/sC. 若传送带顺时针匀速转动,v B 一定等于3 m/sD.情况,从而确定其是否受到滑动摩擦力作用。

牛顿运动定律的应用之传送带模型1.水平传送带水平传送带又分为两种情况:物体的初速度与传送带速度同向(含物体初速度为0)或反向.在匀速运动的水平传送带上,只要物体和传送带不共速,物体就会在滑动摩擦力的作用下,朝着和传送带共速的方向变速(若v物<v传,则物体加速;若v物>v传,则物体减速),直到共速,滑动摩擦力消失,与传送带一起匀速运动,或由于传送带不是足够长,在匀加速或匀减速过程中始终没达到共速.计算物体与传送带间的相对路程要分两种情况:①若二者同向,则Δs=|s传-s物|;①若二者反向,则Δs=|s传|+|s物|.2.倾斜传送带物体沿倾角为θ的传送带传送时,可以分为两类:物体由底端向上运动,或者由顶端向下运动.解决倾斜传送带问题时要特别注意mg sin θ与μmg cos θ的大小和方向的关系,进一步判断物体所受合力与速度方向的关系,确定物体运动情况.【题型1】如图所示,水平传送带正在以v=4 m/s的速度匀速顺时针转动,质量为m=1 kg 的某物块(可视为质点)与传送带之间的动摩擦因数μ=0.1,将该物块从传送带左端无初速度地轻放在传送带上(g取10 m/s2).(1)如果传送带长度L=4.5 m,求经过多长时间物块将到达传送带的右端;(2)如果传送带长度L=20 m,求经过多长时间物块将到达传送带的右端.【题型2】如图所示,足够长的水平传送带,以初速度v0=6 m/s顺时针转动.现在传送带左侧轻轻放上m=1 kg的小滑块,与此同时,启动传送带制动装置,使得传送带以恒定加速度a=4 m/s2减速直至停止;已知滑块与传送带的动摩擦因数μ=0.2,设最大静摩擦力等于滑动摩擦力.滑块可以看成质点,且不会影响传送带的运动,g=10 m/s2.试求:(1)滑块与传送带共速时,滑块相对传送带的位移;(2)滑块在传送带上运动的总时间t.【题型3】如图所示,倾角为37°,长为l=16 m的传送带,转动速度为v=10 m/s,动摩擦因数μ=0.5,在传送带顶端A处无初速度地释放一个质量为m=0.5 kg的物体.已知sin 37°=0.6,cos 37°=0.8,g=10 m/s2.求:(1)传送带顺时针转动时,物体从顶端A滑到底端B的时间;(2)传送带逆时针转动时,物体从顶端A滑到底端B的时间.【题型4】如图所示为货场使用的传送带的模型,传送带倾斜放置,与水平面夹角为θ=37°,传送带AB足够长,传送皮带轮以大小为v=2 m/s的恒定速率顺时针转动.一包货物以v0=12 m/s的初速度从A端滑上倾斜传送带,若货物与皮带之间的动摩擦因数μ=0.5,且可将货物视为质点.(g=10 m/s2,已知sin 37°=0.6,cos 37°=0.8)(1)求货物刚滑上传送带时加速度为多大?(2)经过多长时间货物的速度和传送带的速度相同?这时货物相对于地面运动了多远?(3)从货物滑上传送带开始计时,货物再次滑回A端共用了多少时间?【题型5】在民航和火车站可以看到用于对行李进行安全检查的水平传送带。


微专题四动力学中的“木板-滑块”和“传送带”模型动力学中“木板-滑块”模型1.模型分析模型概述(1)滑块、滑板是上下叠放的,分别在各自所受力的作用下运动,且在相互的摩擦力作用下相对滑动.(2)滑块相对滑板从一端运动到另一端,若两者同向运动,位移之差等于板长;若反向运动,位移之和等于板长.(3)一般两者速度相等为“临界点”,要判定临界速度之后两者的运动形式。
常见情形滑板获得一初速度v0,则板块同向运动,两者加速度不同,x板>x块,Δx=x板-x块,最后分离或相对静止滑块获得一初速度v0,则板块同向运动,两者加速度不同,x板<x块,Δx=x块-x板,最后分离或相对静止开始时板块运动方向相反,两者加速度不同,最后分离滑板或滑块受到拉力作用,要判断两者是否有相对运或相对静止,Δx=x块+x板动,以及滑板与地面是否有相对运动2。
常见临界判断(1)滑块恰好不滑离木板的条件:滑块运动到木板的一端时,滑块与木板的速度相等.(2)木板最短的条件:当滑块与木板的速度相等时滑块滑到木板的一端.(3)滑块与木板恰好不发生相对滑动的条件:滑块与木板间的摩擦力为最大静摩擦力,且二者加速度相同。
[典例1]一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4。
5 m,如图(a)所示。
t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1 s时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板。
已知碰撞后1 s时间内小物块的v。
t图线如图(b)所示。
木板的质量是小物块质量的15倍,重力加速度大小g取10 m/s2。
求:图(a)图(b)(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2;(2)木板的最小长度;(3)木板右端离墙壁的最终距离.[大题拆分]第一步:分析研究对象模型.设小物块和木板的质量分别为m和M。

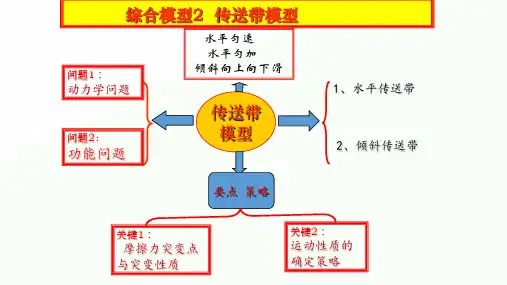





牛顿运动定律的应用----传送带问题1.模型特征(1)水平传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2(1)v0>v时,可能一直减速,也可能先减速再匀速(2)v0<v时,可能一直加速,也可能先加速再匀速情景3 (1)传送带较短时,滑块一直减速达到左端(2)传送带较长时,滑块还要被传送带传回右端.其中v0>v返回时速度为v,当v0<v返回时速度为v0(2)倾斜传送带模型项目图示滑块可能的运动情况情景1(1)可能一直加速(2)可能先加速后匀速情景2 (1)可能一直加速(2)可能先加速后匀速(3)可能先以a1加速后以a2加速情景3 (1)可能一直加速(B点离开)(2)可能一直减速(B点离开)(3)可能一直匀速(B点离开)(4)可能先减速后反向加速(A点离开)(5)可能先减速后加速最后匀速(A点离开)2.模型动力学分析(1)传送带模型问题的分析流程3.传送带问题的解题思路题型练习一:水平传送带1:情景1(1)可能一直加速(2)可能先加速后匀速例题分析(1)先加速后匀速例1 . 水平传送带被广泛地应用于车站、码头,工厂、车间。
如图所示为水平传送带装置示意图,绷紧的传送带AB始终保持v0=2 m/s的恒定速率运行,一质量为m的工件无初速度地放在A处,传送带对工件的滑动摩擦力使工件开始做匀加速直线运动,设工件与传送带间的动摩擦因数为μ=0.2 ,AB 的之间距离为L =10m ,g 取10m/s 2 .求工件从A 处运动到B 处所用的时间.分析 工件无初速度地放在传送带上,由于传送带以2 m/s 的恒定速度匀速运动,工件在传送带上受到传送带给予的滑动摩擦力作用做匀加速运动,当工件加速到与传送带速度相等时,如果工件没有滑离传送带,工件在传送带上再不相对滑动,两者一起做匀速运动.解答 设工件做加速运动的加速度为a ,加速的时间为t 1 ,加速运动的位移为l ,根据牛顿第二定律,有:μmg=ma 代入数据可得:a =2 m/s 2工件加速运动的时间t 1=a v 0 代入数据可得: t 1=1s 此过程工件发生的位移l =12at 12 代入数据可得:l =1m由于l <L ,所以工件没有滑离传送带设工件随传送带匀速运动的时间为t 2 ,则t 2=vl L 代入数据可得:t 2=4.5s所以工件从A 处运动到B 处的总时间t =t 1+t 2=5.5 s(2)可能一直加速例 2. 水平传送带被广泛地应用于车站、码头,工厂、车间。
牛顿运动定律的应用-牛顿运动定律的应用之传送带模型一、模型特征vv≥0) 一个物体以速度在另一个匀速运动的物体上开始运动的力学系统可看做“传送带”模型,(00如图 (a)、(b)、(c) 所示。
二、传送带模型的一般解法①确定研究对象;②分析其受力情况和运动情况,(画出受力分析图和运动情景图),注意摩擦力突变对物体运动的影响;③分清楚研究过程,利用牛顿运动定律和运动学规律求解未知量。
三、注意事项1. 传送带模型中要注意摩擦力的突变①滑动摩擦力消失②滑动摩擦力突变为静摩擦力③滑动摩擦力改变方向2.传送带与物体运动的牵制。
牛顿第二定律中a是物体对地加速度,运动学公式中S是物体对地的位移,这一点必须明确。
3. 分析问题的思路:初始条件→相对运动→判断滑动摩擦力的大小和方向→分析出物体受的合外力和加速度大小和方向→由物体速度变化再分析相对运动来判断以后的受力及运动状态的改变。
【名师点睛】1. 在确定研究对象并进行受力分析之后,首先判定摩擦力突变(含大小和方向)点,给运动分段。
传送带传送的物体所受的摩擦力,不论是其大小的突变,还是其方向的突变,都发生在物体的速度与传送带速度相等的时刻。
物体在传送带上运动时的极值问题,不论是极大值,还是极小值,也都发生在物体速度vv相同的时刻是运动分段的关键点,也是解题的突破口。
与与传送带速度相等的时刻。
传物vv的大小与方向,对二者与(即相对运动方向和对地速度变化)的关键是2. 判定运动中的速度变化传物的比较是决定解题方向的关键。
mgFF的突变情况。
sin θ与的大小与方向,判断3. 在倾斜传送带上需比较ff 4. 考虑传送带长度——判定临界之前是否滑出;物体与传送带共速以后物体是否一定与传送带保持相对静止。
1四、传送带模型问题包括水平传送带问题和倾斜传送带问题1. 水平传送带问题1情景(2)可能先加速后匀速vv时,可能一直减速,也可能先减速再匀速>(1) 02情景vv 时,可能一直加速,也可能先加速再匀速(2) <0(1)传送带较短时,滑块一直减速达到左端vv返>(2)传送带较长时,滑块还要被传送带传回右端。