川师大学物理第十一章 恒定电流的磁场习题解
- 格式:doc
- 大小:3.81 MB
- 文档页数:21

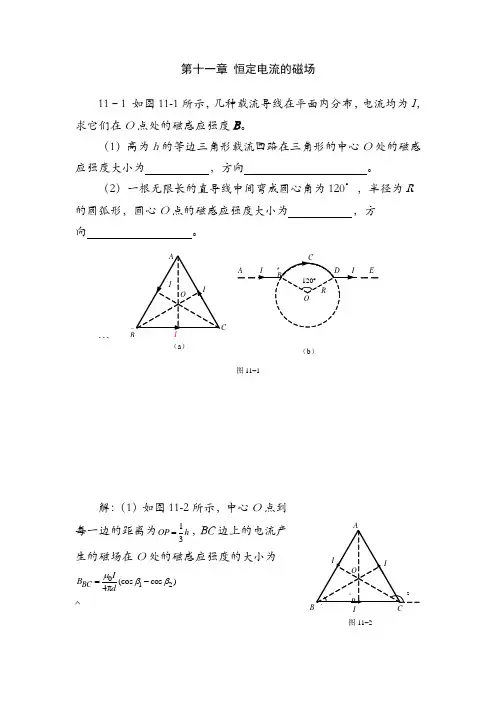
第十一章 恒定电流的磁场11–1 如图11-1所示,几种载流导线在平面内分布,电流均为I ,求它们在O 点处的磁感应强度B 。
(1)高为h 的等边三角形载流回路在三角形的中心O 处的磁感应强度大小为 ,方向 。
(2)一根无限长的直导线中间弯成圆心角为120°,半径为R 的圆弧形,圆心O 点的磁感应强度大小为 ,方向 。
…解:(1)如图11-2所示,中心O 点到每一边的距离为13OP h =,BC 边上的电流产生的磁场在O 处的磁感应强度的大小为012(cos cos )4πBC I B dμββ=-^IB21图11–2图11–1…B(a )AE(b )0(cos30cos150)4π/3Ih μ︒︒=-=方向垂直于纸面向外。
另外两条边上的电流的磁场在O 处的磁感应强度的大小和方向都与BC B 相同。
因此O 处的磁感应强度是三边电流产生的同向磁场的叠加,即3BC B B ===方向垂直于纸面向外。
(2)图11-1(b )中点O 的磁感强度是由ab ,bcd ,de 三段载流导线在O 点产生的磁感强度B 1,B 2和B 3的矢量叠加。
由载流直导线的磁感强度一般公式012(cos cos )4πIB dμββ=- 可得载流直线段ab ,de 在圆心O 处产生的磁感强度B 1,B 3的大小分别为01(cos0cos30)4cos60)IB R μ︒=︒-︒π(0(12πI R μ=-031(cos150cos180)4πcos60IB B R μ︒==︒-︒0(12πI R μ=-】方向垂直纸面向里。
半径为R ,圆心角α的载流圆弧在圆心处产生的磁感强度的大小为04πI B Rμα=圆弧bcd 占圆的13,所以它在圆心O 处产生的磁感强度B 2的大小为00022π34π4π6II I B R R Rμμαμ===方向垂直纸面向里。
因此整个导线在O 处产生的总磁感强度大小为000012333(1)(1)0.212π22π26I I I I B B B B R R R Rμμμμ=++=-+-+=方向垂直纸面向里。

第十一章:恒定电流的磁场习题解答1.题号:40941001分值:10分如下图所示,是一段通有电流I 的圆弧形导线,它的半径为R ,对圆心的张角为θ。
求该圆弧形电流所激发的在圆心O 处的磁感强度。
解答及评分标准:在圆弧形电流中取一电流元l Id (1分),则该电流元l Id 在圆心处的磁感强度为:θπμπμd R I RIdl dB 490sin 40020==(2分) 其中θRd dl =则整段电流在圆心处的磁感强度为:θπμθπμθRI d R I dB B 44000===⎰⎰(2分)2.题号:40941002分值:10分一无限长的载流导线中部被弯成圆弧形,如图所示,圆弧形半径为cm R 3=,导线中的电流为A I 2=。
求圆弧形中心O 点的磁感应强度。
解答及评分标准:两根半无限长直电流在O 点的磁感应强度方向同为垂直图面向外,大小相等,以垂直图面向里为正向,叠加后得RI R I B πμπμ242001-=∙-= (3分) 圆弧形导线在O 点产生的磁感应强度方向垂直图面向里,大小为RI R I B 83432002μμ==(3分) 二者叠加后得 T RI R I B B B 500121081.1283-⨯=-=+=πμμ (3分) 方向垂直图面向里。
(1分)3.题号:40941003分值:10分难度系数等级:1一段导线先弯成图(a )所示形状,然后将同样长的导线再弯成图(b )所示形状。
在导线通以电流I 后,求两个图形中P 点的磁感应强度之比。
(a ) (b )解答及评分标准:图中(a )可分解为5段电流。
处于同一直线的两段电流对P 点的磁感应强度为零,其他三段在P 点的磁感应强度方向相同。
长为l 的两段在P 点的磁感应强度为 lI B πμ4201= (2分) 长为2l 的一段在P 点的磁感应强度为 l I B πμ4202=(2分) 所以lI B B B πμ22012=+= (2分) 图(b )中可分解为3段电流。

一.选择题:1.(基础训练1)[D ]载流的圆形线圈(半径a1)与正方形线圈(边长a2 )通有相同电流I.若两个线圈的中心O1、O2处的磁感强度大小相同,则半径a1与边长a2之比a1∶a2为(A) 1∶1 (B) π2∶1(C) π2∶4 (D) π2∶8提示()82,,22135cos45cos244,2212212121ππμπμμ===-⨯⨯⨯==aaBBaIaIBaIBoooo得由2.(基础训练3)[B ].有一无限长通电流的扁平铜片,宽度为a,厚度不计,电流I在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b处的P点(如图)的磁感强度B的大小为(A))(2baI+πμ.(B)bbaaI+πln2μ.(C)bbabI+πln2μ.(D))2(baI+πμ.提示:bbaaIrdraIrrdIdBdraIdIabb+======⎰⎰⎰+ln222dIBBB,BdB,2P,)(drrPπμπμπμπμ的大小为:,的方向也垂直纸面向内据方向垂直纸面向内;根处产生的它在,电流为导线相当于一根无限长的直的电流元处选取一个宽度为点为在距离3. .(基础训练4)[D ]如图,两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I从a端流入而从d端流出,则磁感强度B沿图中闭合路径L的积分⎰⋅LlBd(A) I0μ.(B) I031μ.(C) 4/Iμ.(D) 3/2Iμ.提示⎰∑⎰=⋅∴=-==∴===⋅LLIl dBIIslIIslIslIIIl dB32322)(RRRIRI11122112122111Lμρρρμμ得为两条支路的电阻。
,,其中,而内4. 自测提高7[C ]如图,正方形的四个角上固定有四个电荷量均为q 的点电荷.此正方形以角速度ω 绕AC 轴旋转时,在中心O 点产生的磁感应强度大小为B 1;此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感应强度的大小为B 2,则B 1与B 2间的关系为(A) B 1 = B 2. (B) B 1 = 2B 2.(C) B 1 =21B 2. (D) B 1 = B 2 /4. 提示: 设正方形边长为a ,)22(a b b OC AO ===式中, 两种情况下正方形旋转时的角速度ω 相同,所以每个点电荷随着正方形旋转时形成的等效电流相同, 为 πω2q I =当正方形绕AC 轴旋转时,一个点电荷在O 点产生的磁感应强度的大小为bIB 20μ=,实际上有两个点电荷同时绕AC 旋转产生电流,在O 点产生的总磁感应强度的大小为b IbIB B 001222μμ=⨯==同理,当正方形绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感应强度的大小为bIb IB B 0022244μμ=⨯== 故有122B B =5. 附录C 2[ B ]有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数为2=N 的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感应强度和磁矩分别是原来的:(A) 4倍和1/8 (B) 4倍和1/2 (C) 2倍和1/4 . (D) 2倍和1/2提示:由半径为R 的单匝线圈弯成匝数为2=N 的线圈以后,每一个线圈的半径变为R r 21=,故磁感应强度变为原来的4倍,磁矩变为原来的1/2,总的变化为4倍和1/2二. 填空题6.(基础训练11)均匀磁场的磁感强度B 与半径为r 的圆形平面的法线n的夹角为α ,今以圆周为边界,作一个半球面S ,S 与圆形平面组成封闭面如所示.则通过S 面的磁通量Φ = απcos 2B r -。

第十一章 恒定电流的磁场(一)一、选择题[ B ]1.(基础训练3)有一无限长通电流的扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b 处的P 点(如图)的磁感强度B 的大小为(A) )(20b a I +πμ. (B) b ba a I +πln 20μ.(C) b ba b I +πln 20μ. (D) )2(0b a I +πμ. 【提示】在距离P 点为r 处选取一个宽度为dr 的电流(相当于一根无限长的直导线),其电流为IdI dr a =,它在P 处产生的磁感应强度为02dI dB rμπ=,方向垂直纸面朝内;根据B dB =⎰得:B 的方向垂直纸面朝内,B 的大小为000dI B ln 222b a b I I dr a br a r a bμμμπππ++===⎰⎰.[ D ]2、(基础训练4)如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分⎰⋅Ll B d 等于 (A) I 0μ. (B)I 031μ. (C) 4/0I μ. (D) 3/20I μ.【提示】如图,设两条支路电流分别为I 1和I 2,满足1122I R I R =,其中12R R ,为两条支路的电阻,即有1211212()l l l I I I I s s s ρρρ==-,得:123I I = 根据安培环路定理,0001L 23内LIB dl I I μμμ⋅===∑⎰, [D ]3、(自测提高1)无限长直圆柱体,半径为R ,沿轴向均匀流有电流.设圆柱体内( r < R )的磁感应强度为B i ,圆柱体外( r > R )的磁感应强度为B e ,则有 (A) B i 、B e 均与r 成正比. (B) B i 、B e 均与r 成反比. (C) B i 与r 成反比,B e 与r 成正比.(D) B i 与r 成正比,B e 与r 成反比. 【提示】用安培环路定理,0 2内L B r I πμ⋅=∑,可得: 当r<R 时 022Ir B R μπ=; 当 r > R 时 02IB rμπ=.[ C ]4、(自测提高7) 如图11-49,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷。





第十一章恒定电流与恒定磁场一、选择题1.如图11-1所示,有两根载有相同电流的无限长直导线,分别通过x1=1m、x2=3m的点,且平行于y轴,则磁感应强度B等于零的地方是()。
A.x=2m的直线上B.在x>2m的区域C.在x<1m的区域D.不在x、y平面上图11-11.【答案】A。
解析:根据对称性可得,两条载流导线在x=2m的直线上产生的磁感应强度大小相等;用右手螺旋定则可判断两磁感应强度的方向相反,相互抵消,合磁感应强度为零,故选A。
2.图11-2中6根无限长导线互相绝缘,通过电流均为I,区域Ⅰ、Ⅰ、Ⅰ、Ⅰ均为全等的正方形,哪一个区域指向纸内的磁通量最大()。
A. Ⅰ区域B. Ⅰ区域C. Ⅰ区域D. Ⅰ区域2.【答案】B。
解析:通过Ⅰ区域的磁通量为0,通过Ⅰ区城的磁通量最大且指向纸内,通过Ⅰ区域的磁通量最大但指向纸外,通过IV区域的磁通量为0。
故选B。
3.如图11-3所示,在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知()。
A.d 0LB l ⋅=⎰,且环路上任意一点B =0 B.d 0LB l ⋅=⎰,且环路上任意一点B ≠0 C.d 0LB l ⋅≠⎰,且环路上任意一点B ≠0 D.d 0LB l ⋅≠⎰,且环路上任意一点B =常量3.【答案】B 。
解析:根据安培环路定理,闭合回路内没有电流穿过,所以环路积分等于0.但是由于圆形电流的存在,环路上任意一点的磁感应强度都不等于0。
故选B 。
4.无限长直圆柱体,半径为R ,沿轴向均匀流有电流,设圆柱体内(r <R )的磁感应强度为B i ,圆柱体外(r>R )的磁感应强度为B e ,则有:()。
A.B i 、B e 均与r 成正比B.B i 、B e 均与r 成反比C.B i 与r 成反比,B e 与r 成正比D.B i 与r 成正比,B e 与r 成反比4.【答案】B 。
解析:导体横截面上的电流密度2πR I J =,以圆柱体轴线为圆心,半径为r 的同心圆作为安培环路,当r <R ,20ππ2r J r B i ⋅=⋅μ,20π2R IrB i μ=;当r <R ,I r B e ⋅=⋅0π2μ,rIB e π20μ=;所以选D 。
第十一章 电流与磁场11-1 电源中的非静电力与静电力有什么不同?答:在电路中,电源中非静电力的作用是,迫使正电荷经过电源内部由低电位的电源负极移动到高电位的电源正极,使两极间维持一电位差。
而静电场的作用是在外电路中把正电荷由高电位的地方移动到低电位的地方,起到推动电流的作用;在电源内部正好相反,静电场起的是抵制电流的作用。
电源中存在的电场有两种:1、非静电起源的场;2、稳恒场。
把这两种场与静电场比较,静电场由静止电荷所激发,它不随时间的变化而变化。
非静电场不由静止电荷产生,它的大小决定于单位正电荷所受的非静电力,q非F E =。
当然电源种类不同,非F 的起因也不同。
11-2静电场与恒定电场相同处和不同处?为什么恒定电场中仍可应用电势概念? 答:稳恒电场与静电场有相同之处,即是它们都不随时间的变化而变化,基本规律相同,并且都是位场。
但稳恒电场由分布不随时间变化的电荷产生,电荷本身却在移动。
正因为建立稳恒电场的电荷分布不随时间变化,因此静电场的两条基本定理,即高斯定理和环路定理仍然适用,所以仍可引入电势的概念。
11-3一根铜导线表面涂以银层,当两端加上电压后,在铜线和银层中,电场强度是否相同?电流密度是否相同?电流强度是否相同?为什么? 答:此题涉及知识点:电流强度d sI =⋅⎰j s ,电流密度概念,电场强度概念,欧姆定律的微分形式j E σ=。
设铜线材料横截面均匀,银层的材料和厚度也均匀。
由于加在两者上的电压相同,两者的长度又相等,故铜线和银层的场强E 相同。
由于铜线和银层的电导率σ不同,根据j E σ=知,它们中的电流密度j 不相同。
电流强度d sI =⋅⎰j s ,铜线和银层的j不同但相差不太大,而它们的横截面积一般相差较大,所以通过两者的电流强度,一般说来是不相同的。
11-4一束质子发生侧向偏转,造成这个偏转的原因可否是:(1)电场?(2)磁场?(3)若是电场和磁场在起作用,如何判断是哪一种场?答:造成这个偏转的原因可以是电场或磁场。
第11章 稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈,分别用图11-1中所示的两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为:[ ](A )10B =,20B =(B )10B =,02IB lπ=(C)01IB lπ=,20B =(D)01I B l π=,02IB lπ= 答案:C解析:有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-,并结合右手螺旋定则判断磁感应强度方向,按照磁场的叠加原理,可计算01IB lπ=,20B =。
故正确答案为(C )。
11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,如图11-2所示,则在圆心O 处的磁感应强度大小为多少? [ ]习题11-1图习题11-2图(A )0 (B )R I 2/0μ (C )R I 2/20μ (D )R I /0μ 答案:C解析:圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==,按照右手螺旋定则判断知1B 和2B 的方向相互垂直,依照磁场的矢量叠加原理,计算可得圆心O处的磁感应强度大小为0/2B I R =。
11-3 如图11-3所示,在均匀磁场B 中,有一个半径为R 的半球面S ,S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α,则通过该半球面的磁通量的大小为[ ](A )B R 2π (B )B R 22π (C )2cos R B πα (D )2sin R B πα 答案:C解析:通过半球面的磁感应线线必通过底面,因此2cos m B S R B παΦ=⋅=。
故正确答案为(C )。
11-4 如图11-4所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ何变化?[ ](A )Φ增大,B 也增大 (B )Φ不变,B 也不变 (C )Φ增大,B 不变 (D )Φ不变,B 增大I习题11-4图习题11-3图答案:D解析:根据磁场的高斯定理0SBdS Φ==⎰,通过闭合曲面S 的磁感应强度始终为0,保持不变。
第十一章 恒定电流的磁场11–1 如图11-1所示,几种载流导线在平面内分布,电流均为I ,求它们在O 点处的磁感应强度B 。
(1)高为h 的等边三角形载流回路在三角形的中心O 处的磁感应强度大小为 ,方向 。
(2)一根无限长的直导线中间弯成圆心角为120°,半径为R 的圆弧形,圆心O 点的磁感应强度大小为 ,方向 。
…解:(1)如图11-2所示,中心O 点到每一边的距离为13OP h =,BC 边上的电流产生的磁场在O 处的磁感应强度的大小为012(cos cos )4πBC IB dμββ=-^00(cos30cos150)4π/34πI I h hμ︒︒=-=方向垂直于纸面向外。
另外两条边上的电流的磁场在O 处的磁感应强度的大小和方向都与BC B 相同。
因此O 处的磁感应强度是三边电流产生的同向磁场的叠加,即3BC B B ===方向垂直于纸面向外。
(2)图11-1(b )中点O 的磁感强度是由ab ,bcd ,de 三段载流导线在O 点产生的磁感强度B 1,B 2和B 3的矢量叠加。
由载流直导线的磁感强度一般公式012(cos cos )4πIB dμββ=-可得载流直线段ab ,de 在圆心O 处产生的磁感强度B 1,B 3的大小分别为01(cos0cos30)4cos60)IB R μ︒=︒-︒π(0(12πI R μ=031(cos150cos180)4πcos60IB B R μ︒==︒-︒0(12πI R μ= 】IB 2图11–2图11–1…B(a )AE(b )方向垂直纸面向里。
半径为R ,圆心角α的载流圆弧在圆心处产生的磁感强度的大小为04πI B Rμα=圆弧bcd 占圆的13,所以它在圆心O 处产生的磁感强度B 2的大小为00022π34π4π6II I B R R Rμμαμ=== 方向垂直纸面向里。
因此整个导线在O 处产生的总磁感强度大小为000012333(1)(1)0.212π2π6I I II B B B B R R R Rμμμμ=++=-+-+=方向垂直纸面向里。
11–2 载流导线形状如图所示(图中直线部分导线延伸到无穷远),求点O 的磁感强度B 。
;图(a )中,B o = 。
图(b )中,B o = 。
图(c )中,B o = 。
…解:载流圆弧导线在圆心O 处激发的磁感强度大小为04πI B Rμα=,式中为载流圆弧导线所张的圆心角,R 为圆弧的半径,I 为所载电流强度。
半无限长载流导线在圆心O 处激发的磁感强度大小为04πIB Rμ=,磁感强度的方向依照右手定则确定。
图11–3(a )中O 处的磁感应强度B O 可视为由两段半无限长载流导线及载流半圆弧激发的磁场在空间点O 的叠加,根据磁场的叠加原理,对于在图(a ),有000004π44π42πo I I I I I B R R R R Rμμμμμ=---=--j k j k j]同样的方法可得对于图(b ),有000001(1)4π44π4π4πo I I I I I B R R R R Rμμμμμ=---=-+-j k k k j对于图(c ),有图11–3xyzOR I…I (a )xyzORII (b ) ¥yxzOR I I (c )00034π84πo I I I B R R Rμμμ=---j k i11–3 已知磁感应强度B =m 2的均匀磁场,方向沿x 轴正向,如图11-4所示,则通过abcd 面的磁通量为 ,通过befc 面的磁通量为 ,通过aefd 面的磁通量为 。
解:匀强磁场B 对S 的磁通量为d cos BS Φθ=⋅=⎰⎰S B S,设各平面S 的法线向外,则通过abcd 面的磁通量为cos π 2.00.40.3abcd BS BS Φ==-=-⨯⨯Wb=通过befc 面的磁通量为πcos 02befc BS Φ==通过aefd 面的磁通量为4cos 2.00.50.35aefd BS Φθ==⨯⨯⨯Wb=11–4 磁场中某点处的磁感应强度B =-(T ),一电子以速度v =×106i +×106j (m/s )通过该点,则作用于该电子上的磁场力F = 。
。
解:电子所受的磁场力为F =e (v ×B )=-×10–19×(×106i +×106j )×-=81014 k (N )11–5 如图11-5所示,真空中有两圆形电流I 1 和 I 2 以及三个环路L 1 L 2 L 3,则安培环路定理的表达式为l B d 1⋅⎰L = ,l B d 2⋅⎰L = ,l B d 3⋅⎰L = 。
<解:由安培环路定理可得101d L I μ⋅-⎰B l =;2012d ()L I I μ⋅+⎰B l =;3d 0L ⋅⎰B l =。
11–6 一通有电流I 的导线,弯成如图11-6所示的形状,放在磁感应强度为B 的均匀磁场中,B 的方向垂直纸面向里,则此导线受到的安培力大小为 ,方向为 。
)图11–5I 1I 2L 1L 2L 3 L 2图11–7III yxB·d F 1d F xd F 1y RdLOyxO¥Bz f b ca d30cm 30cm40cm…50cme 图11–4图11–6》OBII LR解:建立如图11-7所示坐标系,导线可看成两段直导线和一段圆弧三部分组成,两段直导线所受安培力大小相等,方向相反,两力的矢量和叠加后为零。
在半圆弧导线上任取一电流元I d l ,所受安培力大小d =d d sin90d I I lB IB l ⨯=︒=F l B ,方向沿半圆的半径向外。
将d F 分解为d F (垂直于x 轴)和d F //(平行于x 轴),由对称性可知,半圆弧导线所受安培力的水平分量相互抵消为零,即////d 0F F ==⎰其垂直分量;πd d sin d sin sin d 2F F F IB l BIR BIR θθθθ⊥⊥=====⎰⎰⎰⎰方向沿y 轴正方向。
因此,整段导线所受安培力2F =F BIR ⊥=。
方向沿y 轴正方向。
11–7 图11-8中为三种不同的磁介质的B ~H 关系曲线,其中虚线表示的是B =0H的关系,说明a 、b 、c 各代表哪一类磁介质的B ~H 关系曲线: |a 代表 的B ~H 关系曲线;b 代表 的B ~H 关系曲线;c 代表 的B ~H 关系曲线。
答:对各向同性的均匀磁介质,顺磁质或抗磁质有,B =r H ,B 与H 成正比关系,r 为常数,因此曲线bc 代表顺磁质或抗磁质。
又因为顺磁质的r >1,抗磁质的r <1,所以顺磁质的曲线斜率较大,故可进一步判断曲线b 代表顺磁质,曲线c 代表抗磁质,曲线a 中B 与H 成非线性关系,表明该磁介质的r 随H 发生变化,不是常数,这是铁磁质的性质,所以曲线a 代表铁磁质。
11–8 一无限长圆柱体均匀通有电流I ,圆柱体周围充满均匀抗磁质,与圆柱体表面相邻的介质表面上的磁化电流大小为I ´,方向与I 的方向相反。
沿图11-9中所示闭合回路,则三个线积分的值分别为d l ⋅=⎰H l ,d l⋅=⎰B l ,d l⋅=⎰M l 。
¥解:由H 的安培环路定理,得d l I ⋅=⎰H l 。
由B 的安培环路定理,得0d ()l I I μ'⋅=-⎰B l 。
由关系式0μ=-BH M 及上述二式,得d l I '⋅=-⎰M l 。
11–9 半径为R 1的圆形载流线圈与边长为R 2的正方形载流线圈,通有相同的电流I ,若两线圈中心O 1与O 2的磁感应强度大小相同,则半径R 1与边长R 2之比为[ ]。
A 2π:8B .2π:4 C 2π:2 D .1:1解:设两载流线圈中电流I 的方向均为顺时针方向,半径为R 1的圆形载流线圈在中心O 1点产生的磁感应强度大小为0112IB R μ=II ´I ´l图11–9B Oa b c题11–8图方向垂直纸面向里边长为R 2的正方形载流线圈在中心O 2点产生的磁感应强度是各边在该点产生的磁感应强度的叠加,由于各段导线产生的磁感应强度方向相同,均为垂直纸面向里,所以O 2点的磁感应强度大小是各边在该点产生的磁感应强度大小的代数和,有0022222(cos 45cos135)44π/2πIIB R R μμ=︒-︒⨯=…由于B 1= B 2,即0012222πIIR R μμ=因此122πR R = 因此,正确答案为(A )。
11–10 如图11-10所示,在一磁感应强度为B 的均匀磁场中,有一与B 垂直的半径为R 的圆环,则穿过以该圆环为边界的任意两曲面S 1,S 2的磁通量1,2为[]。
A .R 2B ,R 2B B .R 2B ,R 2B C .R 2B ,R 2B D .R 2B ,R 2B解:半径为R 的圆分别与曲面S 1,S 2构成一闭合曲面1,2,规定曲面外法向为曲面面元的正方向,根据磁场的高斯定理,磁感线是闭合曲线,闭合曲面的磁通量为零,则对闭合曲面1有211d d d πd 0R S RB ⋅=⋅+⋅=-+⋅=⎰⎰⎰⎰⎰⎰⎰⎰B S B S B S B S由此可得211d πR B Φ=⋅=⎰⎰B S同理,对闭合曲面2有222d d d πd 0R S RB ⋅=⋅+⋅=+⋅=⎰⎰⎰⎰⎰⎰⎰⎰B S B S B S B S由此可得@222d πRB Φ=⋅=-⎰⎰B S因此,正确答案为(C )。
11–11 如图11-11所示,有两根无限长直载流导线平行放置,电流分别为I 1和I 2,L 是空间一闭曲线,I 1在L 内,I 2在L 外,P 是L 上的一点,今将I 2 在L 外向I 1移近时,则有[ ]。
A .lB d ⋅⎰L与B P 同时改变 B .l B d ⋅⎰L与B P 都不改变,C .l B d ⋅⎰L 不变,B P 改变D .l B d ⋅⎰L改变,B P不变PI 2I 1L图11–11B;S 1 S 2R图11–10解:由真空中的安培环路定理,⎰∑=⋅LI 0d μl B ,∑I 表示穿过回路的电流的代数和,积分回路外的电流I 2不会影响磁感应强度沿回路的积分,但会改变回路上各点的磁场分布,则B P 改变。
因而(C )正确。
11–12 对于介质中的安培环路定理⎰∑=⋅L I l H d ,在下面说法中正确的是[ ]。
A .H 只是穿过闭合环路的电流所激发,与环路外的电流无关B .∑I 是环路内、外电流的代数和C .安培环路定律只在具有高度对称的磁场中才成立D .只有磁场分布具有高度对称性时, 才能用它直接计算磁场强度的大小 解:介质中的安培环路定理⎰∑=⋅L I l H d 在恒定磁场的任何介质中都是成立的,无论磁场是否具有高度的对称性,只是在磁场有高度对称性时,我们可以选择适当的回路,使得待求场点的磁场强度与回路积分无关,其它的线积分为零或与待求场点相同,被积函数H 可从积分号内提出到积分号外,从而可计算出待求场点的磁场强度。