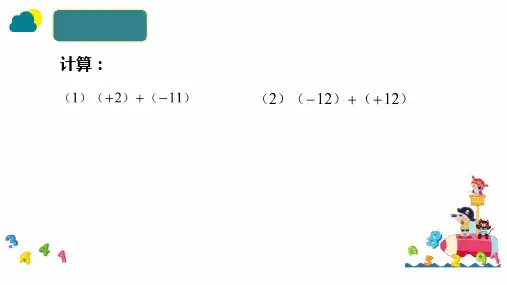当前位置：文档之家 › 《有理数的加法》精品说课课件

《有理数的加法》精品说课课件

  • 格式：ppt
  • 大小：709.50 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

〔华东师大版〕有理数的加法 教学PPT课件(说课)

〔华东师大版〕有理数的加法 教学PPT课件(说课)


↓
同号两数相加
↓↓
取相同符号 通过绝对值化归 为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓
异号两数相加
↓↓
取绝对值较大 通过绝对值化归 的加数的符号 为算术数的减法
同号两数之和——这是名符其实的和，做加法。 异号两数之和——表面上叫“和”，其实是做减法。
运算步骤：
名人名言激励励志名言名语名句100句 （励志 古诗词 篇，附 出处） 51、错误和挫折教训了我们，使我们 比较地 聪明起 来了， 我们的 情就办 得好一 些。任 何政党 ，任何 个人， 错误总 是难免 的，我 们要求 犯得少 一点。 犯了错 误则要 求改正 ，改正 得越迅 速，越 彻底， 越好。 毛泽东
-5 +5
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9 （+5）+（-5）= 0
结论：互为相反数的两个数相加得零。
问题3：在东西走向的马路上，小明从O点出发，向东走-5米，再向东走
0米，两次一共向东走了多少米？
-5
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9 （-5）+ 0 = -5
+5
+3
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9 +8
（+5）+（+3）= +8
(2)向东走-5米，再向东走-3米，两次一共向东走了多少米？
-3
-5
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9 -8 （-5）+（-3）= -8
有理数的加法ppt课件

有理数的加法ppt课件


解：原式 (14) 26 (27) (33) （ 加法的交换律
）
[(14) 26] [(27) (33)] （ 加法的结合律
）
40 (60) （同号两数相加运算法则） ___-2__0___（异号两数相加运算法则）.
练习 7 出租车司机小张某天下午的营运全是在东西方向的大街 上进行的，如果规定向东行驶为正，向西行驶为负，他这天下 午行车全程记录如下：（单位：千米） -3，+16，-11，+12，+18，-16 （1）将最后一名乘客送到目的地时，小张在下午出车的出发 点什么方向，距离多远? （2）若每千米耗油 0.3 升，这天下午小张开车共耗油多少升?
在运算过程中，“先定和 的符号，再算和的绝对 值”，是一种有效的方法.
(5)
1 2
1 2
0
有理数加法的运算步骤： 一、要辨别加数的类型(同号、异号)； 二、要确定和的符号； 三、要计算绝对值的和（或差）.
【思考】任何一个数加上一个正数，和与原来的数有怎 样的大小关系？加上一个负数呢？请你先借助数轴直 观地得出结论，再利用有理数的加法法则进行说明.
任何一个数加上一个负数，和小于原来的数.
我们以前学过加法交换律、结合律，对于有理数的加法它们还 成立吗？
【探究7】 计算：30 + (-20) ，(-20) + 30； 30 + (-20) = 10，(-20) + 30 = 10；
【发现】两个算式的结果相同. 两个算式的第二个算式是由第一个算式交换两个加数的位置 得到的.
2.1.1有理数的加法
第二章 有理数的运算
学习目标
理解有理数加法的意义，掌握有理数的加法运 算法则，能熟练地进行有理数的加法运算. 掌握有理数的加法运算律，并学会运用运算律对 算式进行简化运算.
第1课时有理数的加法法则(39张PPT)数学

第1课时有理数的加法法则(39张PPT)数学


B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
解析
答案
解析 －(－1)＋|－1|＝－(－1)＋1＝1＋1＝2，故选B.
3.下列运算正确的是( )A.(－2)＋(－2)＝0 B.(－6)＋(＋4)＝－10C.0＋(－3)＝3 D.0.56＋(－0.26)＝0.3
1
2
3
4
5
6
7
8
9
10
11
答案
同号两数相加，取与 相同的符号，并把 相加；异号两数相加，取 的符号，并用 减去_____________；互为 的两个数相加得0；一个数同0相加，仍得这个数.
类型2
利用有理数的加法法则运算
解
例2 (教材例1针对训练)计算：
(2)(－39)＋(－11).
解 (－39)＋(－11)＝－(39＋11)＝－50.
解
(4)(－10)＋0.
解 (－10)＋0＝－10.
归纳总结 两个有理数相加的运算方法：(1)同号→确定符号(与加数同号)→把绝对值相加；(2)异号→确定符号(取绝对值较大的加数符号)→较大绝对值减较小绝对值；(3)数＋0＝原数.
0
－8
典例精析
类型1
利用数轴表示两个有理数相加
例1 (教材补充例题)在数轴上表示以下两数相加，并写出结果.(1)(－5)＋(＋3).
解
解 (－5)＋(＋3)＝－2.
解
(2)(－2)＋(－4).
解 (－2)＋(－4)＝－6.
归纳总结 利用数轴表示两个有理数相加的步骤：(1)画数轴；(2)从0开始进行移动；(3)根据终点确定和.
有理数的加法-课件

有理数的加法-课件

8
(+5)+(+3)=8
一个物体向左右方向运动，我们规定向右为正，向左为
负．向右运动5 m记作+5 m，向左运动5 m记作－5 m．
（2）如果物体先向左运动5 m，再向左运动3 m，那么两次运 动后最终的结果是什么？能否用算式表示？
－3 ＋
－5
－8 －7 －6 －5 －4 －3 －2 －1
－8
(－5)＋(－3)＝－8
1.3.1 有理数的加法
第1课时 有理数的加法
•学习目标: 1.通过实例，了解有理数加法的意义， 2.根据有理数的加法法则进行有理数的加法运算。 能运用有理数的加法解决实际问题。 •学习重点:
根据有理数加法法则进行有理数的加法运算。 •学习难点: 有理数加法中的异号两数如何进行加法运算。
两个有理数进行加法运算时，这两 个加数的符号可能有哪些情况？
（2）先向右运动了3 m，再向左运动了5 m，
物体从起点向 左 运动了 2 m ，（+3）＋(－5)＝－；2
（3）先向左运动了5 m，再向右运动了5 m，
物体从起点运动了 0 m ， (－5)＋5＝ 0
．
(－3)＋5= 2
注意观察和的符号与 加数的符号以及和的 绝对值与加数的绝对 值的关系
（+3）＋(－5)＝－2
(－5)＋5＝ 0
根据以上三个算式能否尝试总结异号两数相加的法则？
结论： 绝对值不相等的异号两数相加，取绝对值较大的加 数的符号，并用较大的绝对值减去较小的绝对值， 互为相反数的两个数相加得0 ．
如果物体第1 s向右（或左）运动5 m，第2秒原 地不动，很显然，两秒后物体从起点向右（或左） 运动了5 m.如何用算式表示呢？
有理数的加法(有动画)省公开课获奖课件说课

有理数的加法(有动画)省公开课获奖课件说课


课程简介
掌握有理数的加法运算方法和规则。
能够正确进行有理数的加法运算。
培养学生的数学思维和逻辑思维能力。
课程目标
小学高年级学生和初中学生。
对数学有兴趣，希望学习有理数加法运算的学生。
适用对象
02
教学内容与教学方法
数的产生和扩展
有理数的定义和分类
有理数的加法法则
教学内容
1
教学方法
2
3
通过问题情境的创设，激发学生对数的认知和加法运算的兴趣。
xx年xx月xx日
《有理数的加法(有动画)省公开课获奖课件说课》
CATALOGUE
目录
课程背景教学内容与教学方法课程特色与亮点教学过程与互动设计教学效果与反馈其他相关内容与资源链接
01
课程背景
有理数的加法是数学中的基本运算之一，是进一步学习数学的基础。
本课程以动画形式呈现，通过具体的实例和情境，帮助学生理解有理数的加法运算方法和规则。
有理数加法的动画演示
有些教学视频会配合动画演示来讲解有理数加法的原理和运算过程，这些动画可以帮助学生更好地理解有理数加法的本质。
教学视频资源链接
有理数加法的基本性质
这篇文章详细介绍了有理数加法的基本性质，包括交换律、结合律等，对于学生掌握有理数加法的运算方法有很大的帮助。
有理数加法的实际应用
这篇文章介绍了有理数加法在实际生活中的应用，例如计算温度、计算海拔等，可以帮助学生更好地理解有理数加法的意义和作用。
情境创设
引导学生通过观察、思考和交流，自主探究有理数的加法法则。
探究发现
通过例题和练习，让学生掌握有理数的加法运算，并能够解决实际问题。
实践应用
教学重点
北师大版七年级上册数学《有理数的加法》有理数及其运算说课教学复习课件

北师大版七年级上册数学《有理数的加法》有理数及其运算说课教学复习课件

（来自《点拨》）
知2－讲
例3 下列说法正确的是( B ) A．两个有理数相加，和的绝对值等于它们 的绝对值之和 B．两个负数相加，和的绝对值等于它们的 绝对值之和 C．一个正数和一个负数相加，和的绝对值 等于它们的绝对值之和 D．一个正数和一个负数相加等于0
知2－讲
导引：有理数加法法则包含三个方面的内容：“一 辨”同异号；“二定”和的符号；“三求” 和的绝对值(有加有减)．
知1－导
(2)算出各算式的结果，比较左、右两边算式的结 果是否相同.
(3)请同学们说说自己的结果，你发现了什么？
知1－讲
加法的运算律 交换律：两个数相加，交换加数的位置，和不变， 用字母表示为a＋b＝b＋a. 结合律：三个数相加，先把前两个数相加，或者先 把后两个数相加，和不变， 用字母表示为(a＋b)＋c＝a＋(b＋c)．
第二章 有理数及其运算
2.4 有理数的加法
第1课时
课件
1 课堂讲解 有理数的加法法则
有理数的加法法则的一般应用 有理数的加法的实际应用
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
某班举行知识竞赛，评分标准是：答对一题加1
分，答错一题扣1分，不 回答得0分.
答对一题， 答错一题， 得0分.
答错一题， 答对一题， 得0分.
1 冬天的某天早晨6点的气温是－1 ℃，到了中午气 温比早晨6点时上升了8 ℃，这时的气温是__7_℃___．
2 A为数轴上表示－1的点，将点A沿数轴向右移动2 个单位长度后到点B，则点B所表示的数为( C ) A．－3 B．3 C．1 D．1或－3
（来自《典中点》）
同号两数相加
有理数的 加法类型
－3 仿照上面的例子，计算2 ＋(－5)＝
有理数的加法ppt课件

有理数的加法ppt课件


03
CATALOGUE
有理数加法的运算律
交换律
总结词
有理数加法的交换律是指加法满足交换律，即加法运算不改变数的顺序。
详细描写
交换律是数学中的基本运算律之一，适用于有理数加法。交换律意味着无论数的顺序如何，加法的结 果都是相同的。例如，在有理数中，3 + 4 = 4 + 3，即加数的顺序可以交换，不影响加法的结果。
在0的左边。
绝对值表示一个数到数轴上原点 的距离，正数的绝对值等于其本 身，负数的绝对值等于其相反数
。
有理数的加法、减法、乘法和除 法等运算在数轴上可以通过相应
的位置移动来实现可视化。
02
CATALOGUE
有理数的加法规则
同号有理数相加
总结词
同号有理数相加，取相同的符号，并将绝对值相加。
详细描写
结合律
总结词
有理数加法的结合律是指加法满足结合 律，即加法运算不改变数之间的组合方 式。
VS
详细描写
结合律也是数学中的基本运算律之一，适 用于有理数加法。结合律意味着无论数如 何分组，加法的结果都是相同的。例如， 在有理数中，（3 + 4） + 5 = 3 + （4 + 5），即加数的组合方式可以改变，不 影响加法的结果。
整数与有理数相加
总结词
整数与有理数相加时，先将整数视为特殊的有理数，然后依 照有理数的加法规则进行运算。
详细描写
整数可以视为正有理数或负有理数，因此与任何有理数相加 时，都可以先将其视为特殊的有理数，然后依照有理数的加 法规则进行运算。例如，3（视为+3）和-5相加得到-2。
分数与有理数相加
总结词
04
有理数的加法ppt课件

有理数的加法ppt课件

计算：
计算：
七年级上册有理数
有理数加法的运算律
教学目标
知识与技能
通过验证小学学过 的加法运算律适用 于有理数，并能熟 练运用加法运算律 进行计算。
过程与方法
由加法运算律扩大 到有理数，培养学 生用联系发展的眼 光看待问题。
情感与价值
通过对有理数加 法运算律的探究， 激发学生的求知 欲，体验简单运 算的价值。
巩固练习
计算，并说出它的解题依据和简便方法
解：①23+（-27）+6+（-22） 解题依据
=(23+6) +［(-27)+(-22)]
加法交换律、 加法结合律
=29+(-49)
加法法则
=-20
加法法则
简便方法
正数与正数、负数 与负数分别结合
小结小结
小结有理数加法法则
课外作业： 1. 2、课本第31页2题
a+b=b+a
（a+b)+c=a+(b+c)
例题解析
例1 计算： 16+（-25）+24+（-35）
你能进行简 便运算吗？
解： =[（16+24）]+[（-25）+（-35）] = 40+（-60） = -20
归 纳： 探索了有理数的加法运算律，灵活运 用加法运算律可使运算简便。
有理数加法
巩固练习1 拖动ቤተ መጻሕፍቲ ባይዱ案于对应横线上
重点：有理数加法运算律的验证和运用 难点：灵活利用运算律简化运算
小学学过的加法交换律和结合律 1 两数相加，交换加数的位置，和不变。 a+b=b+a
有理数的加法(有动画)省公开课获奖课件说课

有理数的加法(有动画)省公开课获奖课件说课


03
通过展示学生的成果，鼓励学生积极参与课堂活动，增强学生
的学习自信心。
创新点与突破
创新性引入动画效果
通过动画效果的引入，使学生更加直观地理解有理数的加法规则，提高了学生的学习效率 。
交互式教学的突破
课件中所采用的交互式教学，能够引导学生积极参与，增强学生的主体地位，有效提高了 学生的学习效果。
教材知识点的高度整合
学生活动与作业安排
学生活动
组织学生进行小组讨论、角色扮演等活动，让学生在轻松愉快的氛围中学习。
作业安排
根据教学内容和学生实际情况，布置适量的作业，帮助学生巩固所学知识，提高 学习效果。
05
课程评价与反馈
评价方式与标准
观测点
教学内容、教学目标、教学方 法、教师素养等。
评价标准
制定明确的评价标准，如教学内 容是否符合课程标准要求、教学 目标是否达到预期效果等。
教师评价与反思改进
评价内容
教师对自己在教学内容、教学方法、组织管理等方面进行评价。
反思改进
教师根据评价结果进行反思，及时调整教学策略，改进教学方法 ，提高教学质量。
与学生交流
教师与学生进行交流互动，深入了解学生对教学的需求和意见， 及时调整教学策略，提高教学质量。
06
相关资源与支持
教学资源与工具
3
紧密结合教材
课件内容与教材知识点紧密结合，有利于学生 对知识进行系统掌握。
课程亮点
多元化的教学方法
01
综合运用演示法、讲解法、练习法等多种教学方法，使学生能
够深入理解并掌握有理数的加法。
实际应用案例
02
通过课件中的实际应用案例，让学生了解到有理数加法的实际
有理数的加法ppt课件

有理数的加法ppt课件

在财务管理中，有理数的加法用于计算总收入、总支出和净利润。 例如，一家公司的日收入为200元，支出为150元，净利润是多少呢？
200 + （-150） = 50（元）
Байду номын сангаас
日常生活中的应用
在日常生活中，有理数的加法用于计算购物的总花费、 旅行的总距离等。
例如， 一个人带了100元在超市购物，在超市购买了价值10元、20元 和30元的商品，还有多少钱呢？
0+ (-11) =
加法的结合律
加法的结合律表明，加数的分组方式可以改变，但和不变。 加法结合律: a + (b + c ) = (a + b ) + c
8 + (-10) + (- 8) =[8 + (- 8)] + (- 10) =0 +(- 10) =- 10
有理数加法的实际应用
财务计算中的应用
11 + 0= 11 0+0= 0
有理数加法的运算律
加法的交换律
加法的交换律表明，加数的顺序可以改变，但和不变。 加法交换律: a + b = b + a
5 + 10= 15
10 + 5=
(-11) +(-1) = -12
(-1) + (-11) =
(-5) + 1= -4
1 + (-5)=
(-11) + 0 = -11
加法的基本概念
（１）如果物体沿着一条直线先向左运动３ｍ，再向右运动５ｍ，那 么两次运动的最后结果是什么？如何用算式表示？
（２）如果物体沿着一条直线先向右运动３ｍ，再向左运动５ｍ，那 么两次运动的最后结果是什么？如何用算式表示？
北师大版七年级上册数学《有理数的加法》有理数及其运算教学说课复习课件

北师大版七年级上册数学《有理数的加法》有理数及其运算教学说课复习课件


有理数的加法法则
从上述①- ⑥所写出的算式中 ，你能总结出一些规律吗 ？
① ( + 20) + ( + 30) = + 50 ② ( - 20) + ( - 30) = - 50 ③ ( + 20) + ( - 30) = -10 ④ ( - 20) + ( + 30) = +10 ⑤ ( + 30) + ( - 30) = 0 ⑥ ( -30) + 0 = -30
情境导入
在小学里我们知道，数的加法满足交换律: 例如: 5+3. 5 =3. 5+5； 结合律: 例如：(5+3.5) +2.5 = 5 + (3.5 +2.5).
思考
引进了负数以后，这些运算律是否还成立呢？ 例如：将上面两个等式中，5、3.5和2. 5换成任意的有理数， 是否仍然成立呢？
新课讲解
解法一：这10听罐头的总质量为 444+ 459+ 454+ 459+ 454+ 454+ 449+ 454+ 459+ 464 = 4 550(g). 解法二：把超过标准质量的克数用正数表示，不足的用负数表示， 列出 10听罐头与标准质量的差值表：
听号
1
234
5
与标准质量的差/g －10 ＋5 0 ＋5 0
有理数的加法法则
●
●
-20 -10 0 10 20 30 40 50 60
第一次向西走20米 ，第二次向东走 30米，由数轴表示运动过程可知: 小明位于原来位置的东边10米处即（+10米）
∴( -20) + ( + 30) = + 10,

“有理数的加法”(第1课时)说课ppt 2


（5）（-455）+ 0 = -455 ；
1 1 （6）（- ）+（+ ）= 0 . 2 2
计算： （1）（+26）+（+67）； （2）（-2.3）+（+7.8）； 1 3 （3）（）+（）； 4 2
（5）（-0.673）+0； 7 （6） 0 + （+ ）. 11
5 （4）（+ ）+（-1.375）； 6
问题1：你能用算式来表示这两个实际问题吗？ 问题2：你还能举出类似的生活实例吗？
（一）创设情境，引入新课
2．具体教学安排
（+4）+（-3）= +1
（-2）+（-1）= -3
（二）合作探究，学习新知
1．本阶段需要解决的主要问题
引导学生经历分类、验证、归纳等活
动，探究有理数加法的运算法则，感受分
类讨论的数学思想方法，体会由具体到抽 象、由特殊到一般的认知规律．
不同情况 （ ）+（ ）Байду номын сангаас 5
①同号 |(+2)+(+3)|=5 两数相加
（ ）+（ ）=-5
|(-2）+(-3)|=5
②异号 |(+8）+(-3)|=5 |(-8）+(+3)|=5 两数相加 |(+7）+(-2)|=5 |(-13）+(+8)|=5 ③与零 |(+5 ） +0|=5 |(-5 ） +0|=5 相加
思考： 你能发现得到的结果与两个加数 3 （ ）+（ ）=
2. 具体教学安排

《有理数的加法》有理数及其运算PPT教学课件

2.4 有理数的加法
北师大版七年级上册数学
教学目标
1. 能用具体的情境解释有理数加法； 2. 掌握有理数加法法则，并能熟练进行有理数的加法运算．
情境导入
动物王国举办奥运会，蚂蚁当火炬手，它第一次从数轴上 的原点向正方向跑一个单位，接着向负方向跑一个单位.蚂蚁 经过两次运动后在哪里？如何列算式？
(+1) +(－1)＝ 0
选做：课本36页习题第5、6题.
感谢您 的聆听
宇宙之大，粒子之微，火箭之速，化工之
巧，地球之变，生物之谜，日用之繁，无
处不用数学。
——华罗庚
↓
↓↓
同号两数相加 取相同符号
两个加数的绝对 值相加
(－9) + (+2) = － ( 9－2) =－7
↓↓
异号两数相加
↓
取绝对值较大 的数的符号
较大的绝对值减 去较小的绝对值
小试牛刀
计算下列各题： （1）(－8)＋(－9)
=－(8+9) =－17
（3） 0＋(－13) =－13
（2）(－9.18)+6.18 =－(9.18－6.18) =－3
-3
0
2
4
新知探究
观察与思考
问题2：你能发现以上三个算式中，和的符号、和的 绝对值是怎样确定吗？
新知探究
问题3：以下面几个算式为例，你能归纳出 负数+负数、负数+0 时， 和的符号、绝对值是怎样确定的吗？
(－2) ＋(－3)＝－5
(－3) ＋0＝－3
(－5) ＋(－4)＝－9
(－6) ＋0＝－6
(－9) ＋(－2)＝－11
新知探究 有理数加法法则
(1) 同号两数相加，结果取相同符号，并把绝对值相加． (2) 异号两数相加，结果取绝对值较大的数的符号，并用较大的绝 对值减去较小的绝对值.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

运用新知---信
1.求10＋（－4）
解: 10 ＋（ － 4） = ＋（10 － 4） = ＋6
一看二定三和差
2、（ 1 ）（ 1）
2
6
解：原式 = ( 1 1 )
26
4 6
2 3
化到 最简
1．计算：
（1）(-10)+(-6)； （2）(+12.5)+(-4)； (3) (-0.78)+0．
课堂作业
P24页A组第1题
设 计
1、重点突出情境设置并辅以多媒体动态展示， 形象直观，生动活泼。
特 色
2、注重学生参与探索与归纳的过程，并渗透一 定的数学思想和方法。
3、练习的形式和内容丰富多样，有助学学生很
好地巩固法则。
对以下两种情形，你能表示吗？ （1）第一次向西走了20米，第
二次向东走了20米，
（2）如果第一次向西走了20米， 第二次没有走。
得出新知---省
① +20+（+30）= 50 ② +20+（-30）= -10
+20+(-20)= 0
③ +20+0= 20
-20+（-30）= -50 -20+（+30）= +10 -30+(+30)= 0
法 2、自主探究法
3、总结反思法
本节课我把整个教学过程划分为以下几个环节：
教 1、引入新知---新（创设问题情境） 学 2、探究新知---行 过 3、得出新知---省 程 4、运用新知---信
5、联系实际、小小拓展 6、教学小结、知识回顾 7、课堂作业
引入新知---新
下午放学时，小华的车子坏了，他去修车，不能按时回家，怕妈妈担心， 打电话告诉妈妈，可妈妈坚持要去接他，问他在什么地方修车，他说在 我们学校门前的东西方向的路上，你先走20米，再走30米，就能看到我 了．于是妈妈来到校园门口．
（4）(-5)+(-7)； (5) 4.23+(-6.77) ； (6) 0+(-2.9)
(7) (-9.18)+6.18； (8) -6+6 ； 2．用“＞”或“＜”号填空：
(9)（-2.5）+（
2）
3
(1)如果a＞0，b＞0，那么a+b ______0；
(2)如果a＜0，b＜0，那么a+b ______0；
0+(-20)= -20
两个有理数相 加，和的符号 如何确定？和 的绝对值如何 确定？
有理数加法法则： （1）同号两数相加，取相同的符号， 并把绝对值相加．
（2）绝对值不相等的异号两数相 加，取绝对值较大的加数的符号， 并用较大的绝对值减去较小的绝对 值，互为相反数的两个数相加得0．
（3）一个数同0相加，仍得这个 数．
(3)如果a＞0，b＜0，|a|＞|b|，那么a+b ______0；
(4)如果a＜0，b＞0，|a|＞|b|，那么a+b ______0．
教学小结、知识回顾
1、本节课我们学习到了哪些 主要内容？
2、通过本节课的学习，你体 会到了那些数学思想的方法？
联系实际 小小拓展
已知|a|=3,|b|=4, (1)当a>0,b<0时,求a+b的值 (2)当a,b同号时,求a+b的值 (3)求a+b的值
七年级上册数学
第一课时（说课）
七年级上册数学
一
二
三
四
五
地位和作用
1、有理数加法是初中阶段最基础的Tex运t
算之一。
Text
2、蕴含有丰富的数学思想和方法。
教学目标
知识与能力目标
★ 了解有理数加法的意义 ★ 理解并掌握有理数加法的法则，并会利用法则 进行准确运算，提高学生的运算能力
过程与方法目标
★ 经历法则探索过程，培养学生归纳总结的能力 ★ 在探索过程中感受数形结合和分类讨论的数学思想
情感与态度目标
★让学生体会到数学知识来源于生活，服务于生活， 培养学生对数学的热爱 ★培养学生协作意识，体验成功，树立学习自信心
教学重难点
◆重点 理解和运用有理数的加 法法则
◆难点 理解异号两数相加的加法 法则
若以学校为原点， 规定向东为正，向 西为负，妈妈能找 到他吗？
探究新知---行
联系数轴，运用数轴形象得出上述五个问题的结果。
东
-30 -20 -10 0 10 20 30 40 50 60
1、先向东走20米，再向东走30米； 2、先向西走20米，再向西走30米； 3、先向东走20米，再向西走30米； 4、先向西走20米，再向东走30米。
在教学过程中一如既往的开展“新、行、 省、信”四字教育模式的教学。
教 • 新：创设新的问题情境，开展新的学习方式；
法
• 行：在教师的启发引导下自主、合作探究新知； • 省：在特殊实例的基础上观察、归纳、概括有
理数的加法法则。
• 信：在探究法则与运用法则中体验成功，树立 学习自信心。
学
1、分析归纳法