048_用有限元方法计算电准静态场
- 格式:pdf
- 大小:368.03 KB
- 文档页数:6


第四章 准静态电磁场4.1 准静态电磁场1.电准静态场由麦克斯韦方程组知,时变电场由时变电荷和时变磁场产生的感应电压产生。
时变电荷产生库仑电场,时变磁场产生感应电场。
在低频情况下,一般时变磁场产生的感应电场远小于时变电荷产生的库仑电场,可以忽略。
此时,时变电场满足ρ=∙∇≈⨯∇D 0E 称为电准静态场。
可见,电准静态场与静电场类似,可以定义时变电位函数ϕ ,即ϕ-∇=E且满足泊松方程ερϕ-=∇2 与电准静态场对应的时变磁场满足 0t =∙∇∂∂+=⨯∇B DE H γ 2.磁准静态场由麦克斯韦方程组知,时变磁场由时变传导电流和时变电场产生的位移电流产生。
在低频情况下,一般位移电流密度远小于时变传导电流密度,可以忽略。
此时,时变磁场满足0=∙∇≈⨯∇B J H c称为磁准静态场。
可见,磁准静态场与恒定磁场类似,可以定义时变矢量位函数A ,即A B ⨯∇=且满足矢量泊松方程c J A μ-=∇2与磁准静态场对应的时变电场满足ρ=∙∇∂∂-=⨯∇D B E t例1:图示圆形平板电容器,极板间距d = 0.5 cm ,电容器填充εr =5.4的云母介质。
忽略边缘效应,极板间外施电压t t u 314cos 2110)(=V ,求极板间的电场与磁场。
[解]:极板间的电场由极板上的电荷和时变磁场产生。
在工频情况下,忽略时变磁场的影响,即极板间的电场为电准静态场。
在如示坐标系下,得()()()V/m t 31410113t 31410501102d u z 4z 2z e e e E -⨯=-⨯⨯=-=-cos .cos . 由全电流定律得出,即由()z z 20r 4Sl t 31431410113d t H 2d e e S D l H ∙-π⨯⨯-=∙∂∂=π=∙⎰⎰ρεερφsin . 极板间磁场为φφφρe e H t 314103352H 4sin .-⨯== A/m也可以由麦克斯韦方程直接求解磁场强度,如下tt 0r ∂∂=∂∂=⨯∇E D H εε 展开,得t 314106694H 14sin .)(-⨯=∂∂φρρρ 解得φφφρe e H t 314103352H 4sin .-⨯== A/m 讨论:若考虑时变磁场产生的感应电场,则有tt ∂∂-=∂∂-=⨯∇H B E 0μ 展开,得t E z 314cos 103.231440ρμρ-⨯⨯-=∂∂- 解得 t E z 314cos 10537.428ρ-⨯= V/m可见,在工频情况下,由时变磁场产生的感应电场远小于库仑电场。

基于有限元方法高压开关柜电场的优化设计代佳佳;苗红霞【摘要】高压开关柜的电场分布会影响其绝缘性能,研究和改善高压开关柜中的电场分布是当今高电压技术的重要任务之一.基于有限元软件ANSOFT-MAXWELL 对40.5 kv的高压开关柜内部电场进行3D建模仿真,并分析其静电场分布情况,采用MAXWELL自带的参数化和目标优化设计功能,对高压开关柜内的结构进行优化设计,得到了使高压开关柜内部结构表面电场强度分布最均匀的结构值.【期刊名称】《机械制造与自动化》【年(卷),期】2015(044)002【总页数】5页(P172-176)【关键词】高压开关柜;电场强度;优化设计【作者】代佳佳;苗红霞【作者单位】河海大学能源与电气学院,江苏南京210098;河海大学物联网工程学院,江苏常州213022【正文语种】中文【中图分类】TM591随着国家电网的快速发展和高压开关柜的广泛使用,高压开关柜事故也屡见不鲜。
事故主要表现在绝缘事故、载流故障、机械事故、误动事故和拒动事故等[1-4],其中绝缘事故尤为突出。
由于气体绝缘开关柜采用金属封闭结构,断路器、开关等元器件均密封在SF6气室内,因为SF6气体绝缘性能对电场均匀性的敏感性要远大于空气,所以,在开关柜设计时,必须充分考虑电场的均匀性,使极间及整个场域的电场分布尽可能均匀。
本文采用比较简便实用的有限元分析软件Ansoft-Maxwell自带的参数化和目标优化设计功能。
Ansoft公司的Maxwell是一个功能强大、结果精确、易于使用的电磁场有限元分析软件[5]。
运用其强大的电场分析功能,对绝缘子的高低压端的口径、穿墙套管绝缘管体中部径向安装面板以及内六角螺丝沉头直径进行定性分析,进而实现对开关柜内部结构的优化设计,旨在使其内部电场分布尽可能均匀[6]。
高压开关柜的电场计算是以有限元为理论基础的。
所谓的有限单元法(Finite-Element Method),简称有限元法,是求解数值边值问题以变分原理和剖分插值为基础的一种数值计算方法[7,8]。


几种常用静电场计算方法的探讨摘要:大气中的静电学问题可以归结为求满足边界条件的泊松方程的解。
一般常用的数值解法包括模拟电荷法、有限元法、边界元法以及有限差分方法等。
这些方法都有各自的长处及适用范围,本文将对这几种常用方法进行介绍及比较,并选择合适的方法用于雷暴云大气电场的计算。
关键词:模拟电荷法;有限元法;边界元法;有限差分法处理大气电场观测资料的误差问题,可以采取两种方法。
第一是实验方法,这种方法需要寻找一处受环境影响很小的观测场所,并将一台电场仪安装在这个地方,然后将它的观测结果和需要标定的大气电场仪的观测结果进行对比标定。
但这种方法需要大量的人力、物力和财力,鉴于本项目的既定目标,这种方法可以在今后的业务工作继续完成。
另外一种是理论定标的方法,这种方法采取了准静电场的计算方法,可以在一定程度上去掉一部分由于环境造成的测量误差。
由于目前有关准静电场的计算方法比较成熟,所以这种方法是比较廉价、切实可行的。
本文主要详细介绍几种有关准静电场的计算方法,从理论上论证可以利用这种模式来剔除由于复杂环境造成的部分大气电场测量误差的问题。
1、模拟电荷法模拟电荷法(Charge Simulation Method)是一种求解静电场问题的有效方法,是将原边值问题转化为电源问题来处理的。
它在场域中加入虚拟电荷,用虚拟电荷的影响来等效代替边界的影响,是一种镜像法的推广,国外也有人称为模拟镜像法。
根据唯一性定理,这些虚拟电荷在边界上产生的电位满足给定的边界条件,那么,可以用这些虚设的模拟电荷来计算整个场域的电场。
用模拟电荷法计算电场时,可以根据模拟空间中电极的形状事先给定模拟电荷的类型和数目等,这样,场域中任意点的电位均是由各个模拟电荷的位置和电量决定的,其共同构成的多元函数可以表示为:;(1-1)式中为第个模拟电荷的电量;为第个模拟电荷的位置矢量;为第个场点的位置矢量;为第个模拟电荷对场点的电位系数。
为了更好地保证边界条件,可在边界上选取较多的轮廓点,使表面轮廓点m 大于模拟电荷的个数n,这样,式(1-1)就成为一个超定非线性方程组。




6.641 电磁场、电磁力和电磁运动Markus Zahn 教授第3讲:准静电场和准静磁场及其边界条件I. 准静电场的条件A. 大小评价系数 [ 特征长度L ,特征时间τ ]图3.3.1 包含一个典型长度的模型系统,(a)电动势源驱动一对半径和间距均为L量级的理想导体球的EQS系统。
Hermann A. Haus 和 James R. Melcher赠送,经过允许。
E LE E L ρρρεεε∇⋅=⇒=⇒=2E H E EL L H H t Lεερετττ∂∇×=⇒=⇒==∂232E H H L E E t LL µµρµρµτττ∂∇×=−⇒==⇒=∂误差误差()32222;E L L L C E L C µρµρετρττ====误差 11E LEC τ<<⇒<<误差B. 由准静电场近似引入的误差估计图3.3.2 由分布在外边缘的电动势源驱动的无电阻平行板电极。
Hermann A. Haus 和 James R. Melcher 赠送,经过允许。
0Z Z VE i E i d== 000su E Z d E Z εσε−=⎧=⎨+=⎩202022su su r r d d b b K b b K dtdt dt dEσσππε+=⇒=−=−()20022c SdE dE r H ds E da H r r H t dt φφεππε∂⋅=⋅⇒=⇒=∂∫∫ dt ε da tHds E Sc⋅∂∂−=⋅∫∫µ图3.3.3 表示包含下方平板的体积和平板末梢处的径向面电流密度的图3.3.2平行板。
Hermann A. Haus 和 James R. Melcher赠送,经过允许。
图3.3.4 表示用于计算修正电场的表面和周线的图3.3.2所示子系统的截面。
Hermann A. Haus 和 James R. Melcher赠送,经过允许。

有限元法在标准电容器电场计算中的应用郭天兴,吴俊莉,张建平(西安电力电容器研究所,陕西西安 710082)摘要:本文在分析国外标准电容器有关资料和多年来积累的研究和制造500kV及以下标准电容器经验的基础上,对高压标准电容器的绝缘结构进行了大量的研究工作,并用FORRAN语言编制了有限元法进行标准电容器电场分析和计算的软件。
该软件可用于对标准电容器电场的分析计算和优化设计。
是研究开发高压标准电容器的有效工具。
关键词:标准电容器;有限元法;电场计算he Application of Finite Element Methodsto Electric Field Calculation in the Standard CapacitorGUO ian xing, WU Jun li, ZANG Jian ping(Xi'an power Capacitor Research Institute, Xi'an 710082, China)Abstract:his paper has carried on a large amount of researchwork to the insulation structure of high voltage standard capacitor, based on the analysis of the imported from 100kV Standard capacitor and the experience gained from manufacturing the 500kV standard capacitor in China. he calculating and analyses software use the finite element method has established to the standard capacitor electric field with FORRAN language. his software can used to calculated and analyses the electric field and the optimum design. It is the effective tool to researches and develops the high voltage standare capacitor.Keywords:Standard capacitor; Finite element method; Electric field calculation1 国内外标准电容器发展状况由于标准电容器(以下简称标电)电容量稳定性好,介质损耗小,不受外界条件影响等特点而广泛应用于各种电器设备的绝缘检测,并可用作标准分压器以及局部放电和无线电干扰试验中的耦合电容等,所以,该设备广泛应用于各大电力设备研究所、设备制造业以及电力专业研究院和电力系统现场维护检测等。
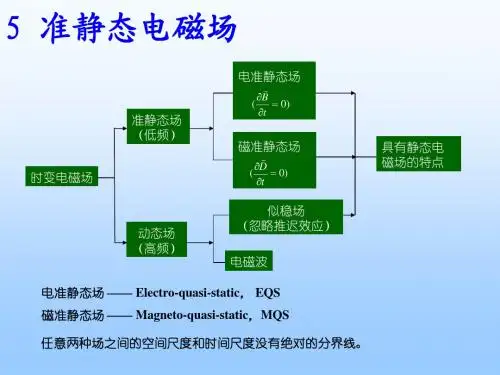
电准静态场与磁准静态场电工基础教研室周学本节的研究目的了解准静态场的性质。
本节的研究内容一、电准静态场与磁准静态场二、磁准静态场与电路⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂-=⨯∇∂∂+=⨯∇f D B tB E tD J H ρ0C 当变化磁场感应出的电场远小于库仑电场时,即0B t ∂≈∂C 00f D D J t B E H ρ⎧⎪∇⋅=⎪⎪⎨∂∇⨯=+⎪∂⎪⎪∇⋅=⎩∇⨯≈与静态场相比,电准静态场具有与静电场类似的有源无旋特性。
因此两种场的计算方法相同。
电力传输系统和装置中的高压电场,各种常用电子器件、设备附近的电场,低频交流情况下,平板电容器中的电场属于电准静态场。
⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂-=⨯∇∂∂+=⨯∇fD B t BE tD J H ρ0C 当位移电流远小于传导电流时,即0Dt ∂≈∂C0f H B B E t D J ρ⎧⎪∇⋅=⎪⎪⎨∂∇⨯=-⎪∂⎪∇⋅=∇⨯⎪⎩≈与静态场相比,磁准静态场具有与静磁场类同的有旋无源特性。
因此两种场的计算方法相同。
运行于低频情况下的各类电磁装置中的磁场问题(电机、变压器、感应加热装置、磁悬浮等等)、电工技术中的涡流问题属于磁准电磁场。
磁准静态场中的位函数引出与时变电磁场相同22(0)Cf A J A μρϕε⎧∇=-∇⋅=⎪⎨∇=-⎪⎩即在准静态电磁场中,可以略去电磁场的波动性,认为场和源之间具有类似于静态场中场和源之间的“瞬时”对应关系。
磁准静态场也称作似稳场。
⎭⎬⎫≡⨯∇⋅∇=⋅∇0)(0A BAB ⨯∇=⇒⎪⎭⎪⎬⎫≡∇⨯∇∂∂-=⨯∇0ϕt B E ϕ∇-∂∂-=⇒tA E似稳条件:对于导体内的时变电磁场来说,当,导体中的时变电磁场可按磁准静态场来处理。
通常把导体中的磁准静态场称作涡流场。
ωεγ<<对于理想介质中的时变电磁场来说,当或,理想介质中的时变电磁场可按磁准静态场来处理。
即如果系统用准静态方法处理,载流系统的尺寸必须远小于电磁波的波长。
2006年用户年会论文
用有限元方法计算电准静态场
石磊,金大志,唐平瀛
(中国工程物理研究院电子工程研究所,四川绵阳,621900)
[ 摘要 ] 本文介绍了电准静态场EQS(Electric Quasi-Static)的控制方程,用通用的大型有限元软件ANSYS计算电准静态场的方法。
通过典型的时谐场和暂态场例题,显示理论分析和数值计算
结果完全符合,可以用到实际的工程问题。
[ 关键词]电准静态,有限元 ,ANSYS
Computation of Quasi-Static Electric Fields with Fea
SHI Lei, JIN Da-zhi,TANG Ping-ying
(Institute of Electronic Engineering, China Academy of Engineering Physics,
Mianyang 621900, China)
[ Abstract ] The controlled equation of Electric Quasi-Static is described. An application of software ANSYS with FEA to the computation of quasi-static electric fields for systems with perfectly
conducting and lossy components is presented. This method shows good agreement
between numerical and analytical calculations for benchmark model, and has been
effectively applied to partical problems.
[ Keyword ] EQS,FEA,ANSYS
1前言
电场强度的计算是高压绝缘设计中必不可少和极为重要的一部分,只考虑介质电导σ的恒流场计算和只考虑绝缘介质介电常数ε的静电场计算早已为人们熟悉[1]。
然而实际的绝缘介质总是有一定的电导,特别是人为的通过一层薄的半导电层来调整绝缘子表面的电
位分布[2],这时电导σ和介电常数ε共同起作用,单纯用恒流场或静电场计算已无能为力,必须采用准静态电场的计算方法。
2控制方程和计算方法
2.1电准静态场控制方程
2006年用户年会论文
电磁场是一种特殊的物质形态,Maxwell 方程组完全描述了电磁场的宏观性质。
电磁场
理论有两个分支:一是从无线电频率到光频的电磁波传播问题,其中特征时间τ比电磁波通过系统的特征长度L 所需时间要短得多即τ<<L/c ;另一个分支是对于频率较低和特征长度较小的系统,其中特征时间τ比电磁波通过时间要长得多即τ>>L/c ,也就是准静态电磁场问题[5]。
实际上很多电工(包括电力工程)学科中的电磁场问题,大多是准静态的。
准静态场绝不是静态场,它是与时间有关的,并且不论那一类准静态场,都是既含有电场又含有磁场,只是电场和磁场之间没有耦合。
当磁感应强度随时间的变化可以忽略时,即
0≈∂∂t B
r ,称为电准静态,简称EQS ,这
时Maxwell 方程组退化为 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅∇=⋅∇≈×∇∂∂+=×∇ρD B E t D J H r r r r r r 00
对
t D J H ∂∂+=×∇r r r 求散度,可以有连续性方程:0(=∂∂+⋅∇t D J r r 由于0≈×∇E r ,电场E r 是无旋的,仍可以用标量位来描述V E −∇=r ,电场与磁场已经是非耦合的,当仅关心电场时,考虑到物性方程:E D E J r r r r εσ==,
可得同时考虑了材料的电导σ和介电常数ε的电准静态场的控制方程为: 0()(=∂∂∇⋅∇−∇⋅∇−t V V εσ
忽略电位随时间的变化它就成了恒流场的控制方程:0)(=∇⋅∇−V σ 在谐性电场分析中,控制方程为可写为:0
)()(=∇⋅∇+
∇⋅∇−V j V σωε
2.2 ANSYS 计算方法
ANSYS 软件是一个大型通用有限元分析软件,在我国有着广泛的应用,它也可以用来
分析电磁领域多方面的问题,自8.1版本后它增加了准静态电场的计算功能。
对于准静态时谐电场的计算,ANSYS 一方面扩充了原有的基于电荷的静电场单元
PLANE121,SOLID122, SOLID123的能力,使它们也能进行准静态时谐电场的计算;另一方面新增了基于电流的准静态电场单元,即PLANE230,SOLID231,SOLID232。
对于准静态暂态电场的计算,ANSYS 只能用新增的准静态电场单元。
2006年用户年会论文
在准静态电场的计算中,要求输入的材料特性是介电常数PERX 和电阻率RSVX ,要
注意的是电阻率是电导率的倒数,而电工书上经常给出的是材料的电导率。
3 计算比较
3.1 时谐场
在均匀的时谐场中,放入一个介质球体,它的表面覆盖有一层薄的导电层,如图1所
示,
在这种情形下,如图1所示最大电场强度的解析解是[3]
))((2)2)(2()(6)2(303132313321333133max
εεεεεεεεεεεεεε−−−++−++=r r d d E E
式中: )3,2
,1(/)(0=+=+=x j r
r d d rx
x x r εωεσε
导电层中的功率损耗为:
a r E P 32036πσ=Δ
图1 表面覆盖有一层薄的导电层的介质球体在均匀时谐场中
式中:
3313213323
2312322321
)
)((2)2)(2()11()
(2)1()
2(r r r d b d b d b a εεεεεεεεεεεεεε−−−++=−−−−+= 取表面厚度d=1mm, 对电导在10-4~10-8S/m 范围内的Emax 解析解的计算结果与有限元
的计算结果见图2,导电层中的功率损耗解析解的计算结果与有限元的计算结果见图3,电导在10-6时的等位线实部和虚部见图4
2006年用户年会论文
图2 电场强度与电导关系 图3 功率损耗与电导关系
图4 等位线实部和虚部从图2可以得出,在频率为50HZ 条件下,当电导值小于10-8时导电层已经对Emax 无
影响,当值大于10-4时导电层相当于浮动电位的电极。
Emax 的最大转变发生在10-5~
10-7S/m ,在这个范围内导电层中的功率损耗达到最大。
3.2 暂态场
具有介电常数εb 、电导率σb 的球形材料被介电常数εa 、电导率σa 的材料包围,
施加一在远离球体处是均匀的电场E(t)[5],如图5所示。
在阶跃电压的激励下,空间电位分布为[5]:
⎪⎪⎩⎪⎪⎨⎧<⎥⎦⎤⎢⎣
⎡+−+−+−+<⎥⎦⎤⎢⎣⎡+−+−+−+−=Φ−−−−R r e e R r r R r R e e R r R E t b a b a t b a b a t b a b a t b a b a ;2)1(21;(2)1(2cos //2//0ττττεεεεσσσσεεεεσσσσθ
当参数的选择满足5/,5/==b a a b εεσσ时,
2006年用户年会论文
图5被εa、σa材料包围的εb、σb球形材料在暂态场中
系统的弛豫时间:τ=(2εa+εb)/(2σa+σb)= 6.96s。
在θ=45度,r = R处时,电位随时间的变化的理论值和ANSYS计算值如图6所示。
用ANSYS计算的这个场的瞬变过程的图解描绘在如图7中,选择所示的这种情况是因为随着时间的推进,它所包含场的急剧的重新分布。
球形区域与它的周围相比是高度导电的,但是外部的材料与球形区域相比是高度可极化的。
因此在开关刚闭合以后,场的分布应是一均匀场施加到完纯电介质情况时的分布。
的确,t=0的图象给出完纯电介质的电位,随着时间的推进传导占统治,经过了多个弛豫时间,电位就变成了稳定传导时的分布,瞬变过程的长短由弛豫时间τ所确定。
图6 θ=45度,r = R处的电位随时间变化
图7 等位线随时间的演变
2006年用户年会论文4结论
准静态电场的应用范围很广,如绝缘子表面的水珠和污秽,高压电机线圈半导电防晕层的设计、真空灭弧室的设计以及电阻式电压传感器的设计等。
用有限元的方法可以有效地进行含有半导电层的准静态电场的分析和计算,它填补了在静电场和恒流场之间的空档,数值计算结果与理论分析完全符合,可以用到实际的工程问题。
商业软件ANSYS的使用将增加建模和计算的方便。
参考文献
[1]解广润. 高压静电场[M],上海科学技术出版社,上海,(1987)
[2]刘子玉. 电气绝缘结构设计原理[M], 机械工业出版社,北京,(1981)
[3]Blaszczyk A. Computation of Quasi-Static Electric Fields with Region-Oriented Charge Simulation [J].IEEE Transactions on magnetics, 1996,32(3), 828~831.
[4]盛剑霓. 电磁场数值分析[M], 西安交通大学出版社, 西安,(1991)
[5]豪斯.H.A 电磁场和电磁能[M].汪家麟.周佩白译, 高等教育出版社,北京,(1992)。