实验十五 数字散斑测量微小位移的实验
- 格式:doc
- 大小:173.50 KB
- 文档页数:4

一种基于快速傅立叶变换的数字散斑系统_位移测量论文导读::本文提出了一种基于快速傅立叶变换的数字散斑系统。
而直接将条纹再进行FFT计算并取强度。
位移测量。
关键词:数字散斑,快速傅立叶变换,FFT,位移测量1. 引言近年来有大量的研究开始基于数字技术对散斑干涉系统进行改进,但一般这些改进的系统只是使用CCD代替全息干板进行二次曝光散斑图的记录,在再现过程中需要应用空间调制器等较贵的电光实时器件,系统构成和软件处理也较为复杂。
本文提出了一种基于快速傅立叶变换的数字散斑系统,仅需使用CCD记录物体位移前后的两幅散斑图,然后直接通过计算散斑图中各处的空间频谱分布,快速获取物像各点的位移大小。
通过实验证明,该方法是有效、且精确的。
系统光路构成简单、算法简明高效,能够有效实现实时的物体位移变化测量,可以满足大量测试场合的需要。
2. 系统构成分析 2.1 基本系统说明传统的散斑干涉记录系统可如图1(a),其逐点扫描的再现系统如图1(b)。
由于散斑系统不需使用干涉方式记录位移测量,对记录材料的分辨率要求较低,便于用CCD进行数字方式的记录。
(a) 记录成像散斑光路示意图(b) 逐点分析法再现光路图1 散斑干涉计量的记录和再现系统示意图实际上,逐点扫描的再现方式是将记录散斑图的局部进行夫琅和费衍射,其干涉条纹图为散斑图经傅立叶变换的空间频谱的强度。
当散斑图被数字化记录后,其空间频谱信息可以在计算机中通过快速傅立叶变换(Fast Fourel Traslation, 即FFT)直接快速计算获得。
系统仅使用一个CCD和散斑成像光路,取消了散斑再现实时光路,所有再现过程均在计算机中计算完成。
同时还可通过计算快速获得位移的大小和方向信息。
2.2使用空间频谱分析获取位移的方法传统方法中通过光学的逐点分析法获取的散斑图的杨氏条纹图像可如图2(a)所示,其圆形的边界是由于入射光为圆细激光束所致。
在后续处理中,该条纹图还需要进一步测量读出条纹间距和方向。
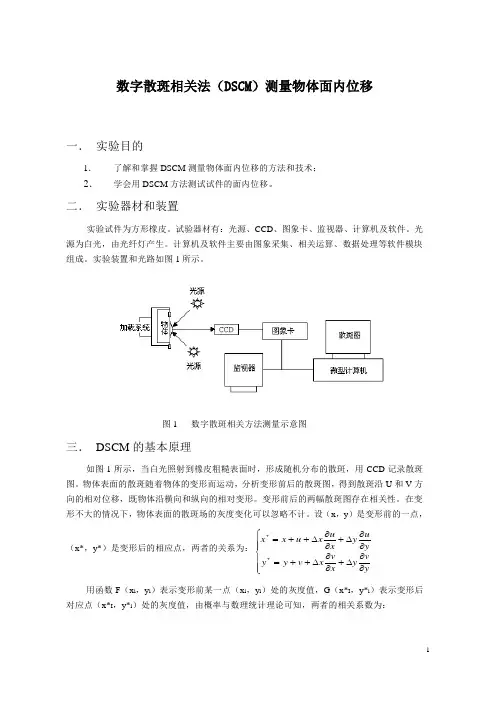
数字散斑相关法(DSCM )测量物体面内位移一. 实验目的1.了解和掌握DSCM 测量物体面内位移的方法和技术; 2.学会用DSCM 方法测试试件的面内位移。
二. 实验器材和装置实验试件为方形橡皮。
试验器材有:光源、CCD 、图象卡、监视器、计算机及软件。
光源为白光,由光纤灯产生。
计算机及软件主要由图象采集、相关运算、数据处理等软件模块组成。
实验装置和光路如图1所示。
图1 数字散斑相关方法测量示意图三. DSCM 的基本原理如图1所示,当白光照射到橡皮粗糙表面时,形成随机分布的散斑,用CCD 记录散斑图。
物体表面的散斑随着物体的变形而运动,分析变形前后的散斑图,得到散斑沿U 和V 方向的相对位移,既物体沿横向和纵向的相对变形。
变形前后的两幅散斑图存在相关性。
在变形不大的情况下,物体表面的散斑场的灰度变化可以忽略不计。
设(x ,y )是变形前的一点,(x*,y*)是变形后的相应点,两者的关系为:⎪⎪⎩⎪⎪⎨⎧∂∂∆+∂∂∆++=∂∂∆+∂∂∆++=y v y x v x v y y y u y x u x u x x **用函数F (x i ,y i )表示变形前某一点(x i ,y i )处的灰度值,G (x*I ,y*i )表示变形后对应点(x*I ,y*i )处的灰度值,由概率与数理统计理论可知,两者的相关系数为:()[]()[]()[]()[]∑∑∑∑∑∑==**====**----=s ss s s sm i m j j im i m j jim i m j j i jigy xg f y x f gy xg f y x f C 11211211,,,,其中0≤C ≤1;C=1时两者完全相关;C=0时两者完全不相关。
分母分别为两者的均方根,分子为两者的相关矩,f 和g 分别为()i i y x f ,和()**i i y x g ,的平均值。
只要两者相关,则以位移为变量的相关函数C(u, v)曲面为一单峰曲面。



水下微小位移的散斑测试方法
王云山;黄小平;潘秉智;刘业厚;王明吉
【期刊名称】《石油学报》
【年(卷),期】1993(14)1
【摘要】一种水下微小位移的激光散斑照相测试方法。
标定恒温时水下微小位移的精度可以达到3%。
在水面上1m高处以每秒0.2滴水的滴定速率的扰动下,从每次曝光1~10秒,能得到微小位移的双曝光散斑图。
测量了16MnR板试件表面裂纹中心张开位移,结合SCOD法计算了相应的表面裂纹应力强度因子K_1。
把板试件的测值与通常情况下的测值和Newman-Raju解的计算值作了比较,三者符合得很好。
把内充油球形容器内表面裂纹应力强度因子K_1的测值和球形容器外表面裂纹应力强度因子K_1的测值,分别与Schmitt-Keim式的结果作了对比,结果符合得很好。
径比接近1的工业球罐表面裂纹应力强度因子K_1的计算,可以不考虑曲率的影响而选择合理的平板解。
【总页数】7页(P131-137)
【关键词】激光散斑照相;容器;裂纹;管道
【作者】王云山;黄小平;潘秉智;刘业厚;王明吉
【作者单位】大庆石油学院
【正文语种】中文
【中图分类】TE973.6
【相关文献】
1.电子剪切散斑干涉技术时间相移法在金属梁微小位移测量中的应用分析 [J], 郑柱
2.几种电子剪切散斑相位求解法在简支梁微小位移测量中的应用比较分析 [J], 郑柱
3.基于空间载波散斑干涉的微小位移测量方法 [J], 宋骆林;林振衡;陈军;宋黎黎
4.数字散斑相关法测量微小位移的模型与算法研究 [J], 黄忠文
5.数字散斑相关法测量微小位移的模型与算法研究 [J], 黄忠文
因版权原因,仅展示原文概要,查看原文内容请购买。

激光散斑干涉实验激光散斑干涉实验摘要:激光散斑测量法是在全息方法基础上发展起来的一种测量方法,这种方法具有很强的实用价值。
散斑位移测量不仅可以实现离面微位移的测量,也可以进行面内微位移测量。
主要是对面内微位移进行了测量研究,利用设计的测量系统将物体发生位移前后的散斑图由CCD记录下来,分别用数字散斑相关法和散斑照相法对散斑图像进行了分析处理,并得出了相应的结论。
关键词:激光散斑;位移测量;数字图像处理一、引言激光自散射体的粗糙表面漫反射或通过透明散射体(毛玻璃等)时,在散射表面或附近的光场中会形成无规则分布的亮暗斑点,称为激光散斑。
激光散斑在全息图上是一种有害的背景噪声,但由于散斑携带了光束和光束所通过物体的光学信息,于是产生了广泛的应用。
例如,用散斑的对比度测量反射表面的粗糙度;利用散斑的动态情况测量物体运动的速度;用散斑进行光学信息处理,甚至利用散斑验光等等。
但应用领域最广的是散斑干涉测量技术。
散斑干涉技术在机械工程方面可以用于测量物体表面的形变和裂纹、损伤和应力分布,在天文学方面可以测量大气的扰动和温度场分布,在医学、力学和光处理等领域也有广泛的影响。
二、实验2.1实验测试系统散斑干涉测量离面位移光路图如下图所示2.2实验原理(1)激光散斑当相干光照射一个粗糙物体的表面(或通过透明的粗糙面)时,在物体表面前的空间,可得到一种无规律分布且明暗相间的颗粒状光斑,称为散斑。
由于激光的高度相干性,表面散射光在空间中随机相干叠加后会形成一些亮暗分明的区域,且呈现无规则分布,按照在散射面有无透镜,可以将散斑场划分为主观散斑和客观散斑,由于透镜的使用,主观散斑又被称为成像散斑。
(2)利用散斑干涉术测量面内位移散斑干涉计量就是将物体表面空间的散斑记录下来,当物体运动或由于受力而产生变形时,这些随机分布的散斑也随之在空间按一定规律运动。
因此能利用记录的散斑图分析物体运动或变形的有关信息。
当测量物体在面内发生位移时,通常在被测物体位移前,将散斑记录下来,然后使物体垂直于光轴发生一微小面内位移d,再次记录。


实验十五 数字散斑测量微小位移的实验实验目的:1. 掌握数字散斑干涉的原理。
2. 学会根据CCD ,激光器等器件,利用计算机进行快速傅立叶变换,测量物体的微小位移。
3. 学会分析思考并处理实验中出现的问题。
实验原理:当一束激光照射到具有漫射特性的粗糙表面上时,在反射光的空间中用一个白色的屏去接收光总可以看到一些斑点,这就是激光散斑现象。
散斑现象是高度相干性光源照明的结果,虽然会降低全息照相时的成像质量,但由于散斑的大小、位移及运动是有规律的,它可以用来进行微小位移的检测、形变测量以及振动研究等。
传统的散斑干涉测量技术采用在同一张底片上记录物体位移前后的双曝光散斑图,并通过会聚透镜进行光学傅立叶变换得到杨氏条纹图。
随着CCD 的日益普及出现了数字散斑干涉技术,散斑图可以方便的记录在计算机中,并使用数字傅立叶变换进行处理和分析,避免了底片冲印测量的繁琐过程,可以实现方便快速的实时测量。
通过CCD 捕获被测物体位移前后的双曝光散斑图,对双曝光散斑图的任一点附近取一小块区域进行两次快速傅立叶变换,可以得到物体位移的方向和距离。
设位移前后的散斑图分别为()21,x x g i 和()2211,u x u x g itd ++,叠加得双曝光散斑图()()()22112121,,,u x u x g x x g x x g itd i +++= (15-1)用快速傅立叶变换对其中一小块区域进行计算,结果为一小幅杨氏条纹图。
()()()[]()[]⎰⎰∆+-∙+++=212211*********exp ,,,dx dx x x j u x u x g x x g G itd i ωωπωω(15-2)上式中,()21,ωωG 为频谱图上的谱面函数,21,ωω为谱面坐标,∆是积分域。
根据傅立叶平移原理,并假设21,u u 很小,可得双曝光散斑图相应的光强为:()()()()()()[]ωπωωωπωωωωωωd V I d I G I g g 2cos 1,2cos ,4,221221'22121+=∙=+= (15-3)式中()21,u u d = ,()21,ωωω=,()1≤V 是杨氏条纹的对比度。

数字散斑相关亚像素位移测量方法研究与实验摘要:本文主要研究数字散斑相关亚像素位移测量方法,通过实验验证了该方法的可行性和有效性。
本文首先介绍了数字散斑相关技术的原理,然后详细阐述了亚像素级位移测量方法,最后通过实验数据验证了该方法的准确性和稳定性。
本文的研究成果对于数字散斑相关技术的应用具有一定的指导意义。
引言:亚像素级位移测量技术在现代工业和科学研究中具有广泛的应用,如显微镜、机器人视觉、医学影像等领域。
传统的位移测量方法通常采用光学干涉、机械接触等方式,这些方法存在一定的局限性和不足之处。
数字散斑相关技术作为一种新型的位移测量方法,具有非接触、高精度、高稳定性等优点,已经成为研究的热点之一。
本文主要研究数字散斑相关亚像素级位移测量方法,并对其进行了实验验证。
相关工作:数字散斑相关技术是一种基于图像处理的位移测量方法,其基本原理是利用两幅图像之间的散斑纹理变化进行位移估计。
该技术具有较高的测量精度和稳定性,已经被广泛应用于许多领域。
近年来,随着计算机技术和图像处理技术的发展,数字散斑相关技术得到了更广泛的应用和发展。
方法:本文采用数字散斑相关亚像素级位移测量方法,具体步骤如下:首先,采集两幅待测目标的图像,并提取其中的散斑纹理特征;然后,利用数字散斑相关算法计算两幅图像之间的散斑纹理变化;最后,根据计算得到的散斑纹理变化进行亚像素级位移估计。
在实验中,我们采用了不同的参数设置和数据集进行了实验验证,以探究算法的性能和稳定性。
实验:我们采用了不同类型和尺寸的散斑纹理进行实验验证,包括随机散斑、周期性散斑和不同尺寸的图案散斑等。
实验结果表明,本文提出的数字散斑相关亚像素级位移测量方法具有较高的准确性和稳定性。

激光散斑法测钢制简支梁微小位移土木建筑学院土木工程0409班郑楠、牙韩胜、张勇激光散斑干涉方法是近20年来发展起来的一种新的实验应力分析方法。
该方法所依据的理论就是相干光相遇时会发生干涉而形成条纹,我们最熟悉的例子是杨氏干涉条纹,而杨氏干涉条纹是由两个点光源发出的波所形成的。
例如用相干性很好的激光照射物体漫反射表面,这些表面漫反射光好像无数小的相干点光源所发出的光,它们之间也是相干光,彼此也要发生干涉,但在很多点光源的情况下,干涉不再具有规律性,而是在物体表面前边的空间形成了无数随机分布的亮点和暗点,这就是散斑。
因为是激光做光源,所以叫激光散斑。
采用成像透镜,将物体表面随机分布的散斑连同物体的象一起用全息底片记录下来,就可得到散斑图。
如采用双曝光法散斑照相进行力学量测,就是将物体变形前的散斑图与变形后的散斑图记录在同一张全息底片上,再将这张带有物体变形信息的底片,放在一定的光路系统中,即可将散斑图中贮存的信息提取出来,即是散斑测量。
实验目的本实验利用激光散斑法和杨氏干涉的原理来达到测量钢制简支梁在不同集中载荷作用下的微小位移,将实验测量结果与理论计算值进行比较分析。
实验原理用激光照射被测物体漫反射表面,形成空间散斑场。
使用成像透镜(可用付里叶镜头或制板镜头,也可用普通放大镜)将激光照射物体表面形成的散斑,记录在全息底片上,得到散斑图。
即在被测物体变形前和变形后进行两次曝光,将两个散斑场记录在同一张底片上,得到带有物体表面变形信息的双曝光散斑图。
将记录了物体位移信息的双曝光散斑图经显影,定影之后,放在一定的光路系统中,便可把散斑图内贮存的变形信息提取出来,即是散斑图分析。
本实验对散斑图分析采用逐点分析法(如图2所示光路)。
当用同一底片对物体变形前后的两种状态做二次曝光,在底片上就得到了物体表面在变形前后的二个散斑图像的迭加。
考虑物体表面的一个微小的区域,这个小区域里各点的位移大小和方向可以看成是相同的,也就是可以认为在物体变形过程中,这个小区域只发生整体移动,这样的小区域称为准平移区。

实验报告陈杨 PB05210097 物理二班实验题目:激光散斑测量实验目的:了解单光束散斑技术的基本概念,并应用此技术测量激光散斑的大小和毛玻璃的面内位移。
实验内容:本实验中用到的一些已知量:(与本次实验的数据略有不同)激光波长λ = 0.0006328mm常数π = 3.14159265CCD像素大小=0.014mm激光器内氦氖激光管的长度d=250mm会聚透镜的焦距f’=50mm激光出射口到透镜距离d1=650mm透镜到毛玻璃距离=d2+P1=150mm毛玻璃到CCD探测阵列面P2=550mm毛玻璃垂直光路位移量dξ和dη, dξ=3小格=0.03mm,dη=0光路参数:P1=96.45mm ρ(P1)=96.47mm P2= 550mm dξ=3小格=0.03mm (理论值)数据及处理:光路参数:P1+d2=15cmP2=52.5cmd1=激光出射口到反射镜的距离+反射镜到透镜距离=33.6+28.5=62.1cm f ’=5cm d=250mm λ=632.8nm(1)理论值S 的计算:经过透镜后其高斯光束会发生变换,在透镜后方形成新的高斯光束 由实验讲义给的公式:2'2012'11''2)()1(d f W f d d f f λπ+---= πλd W 01= 201W d πλ=代入数据,可得:''121221''12222010222222101102d 15(1)()562.11559.6332439.63362.12515511f d f cm P d d f fcm cmP cm cm cm cmcm cm cm cm dW W d d W d f f f f W λππλ⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭-=-=--+-=-+=≈-+==-+-+=可得由公式-31.80010cm ≈⨯此新高斯光束射到毛玻璃上的光斑大小W 可以由计算氦氖激光器的高斯光束的传播特性得到:221/2302022222122112111()(1/)250.16162.12511550.161()19.63319.6349.6339.6331.8001010.1W W a W d cma cmcm cm d d cm cm f f a cm P P cm cm cm P cm P P cm πλρ-⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=+===≈-+-+=+=⨯+≈=⨯⨯+1/220.10861cmcm ⎛⎫⎛⎫ ⎪⎪ ⎪⎝⎭⎝⎭≈可以求得散斑的统计半径S :372632.81052.5cm /9.792100.108cm cm S P W cmλππ--⨯⨯==≈⨯⨯(2)实验值的计算: 组数 Sx/像素 Sy/像素 r S=(S x +S y )/2 1 7.74 8.57 11 8.16 2 7.67 9.00 13 8.38 3 7.53 8.71 12 8.12 4 7.10 8.32 10 7.71 5 7.50 8.46 10 7.98 67.468.37107.92618.056i i S S ===∑像素=112.7μm则S 理论值和实验值得相对误差为:-S 11.27-9.792100%=100%15.1%S 9.792S η=⨯⨯=理论实验理论照在毛玻璃上激光光斑的平均半径:2252.5=632.8nm cm 3.14112.7938.329.3810cm P w m m Sλμμπ-=⨯÷÷==⨯ 则W 的理论值和实验值得相对误差为:9.38-10.8100%=100%13.1%10.8w w w η-=⨯⨯=理论实验理论(3)求出毛玻璃的平均实际位移量 61162246i i d d m ξξμ====∑像素0d η=毛玻璃的平均实际位移量2122434.71()152.5/9.634d mx m P P cm cm ξμμρ∆===++本实验中,调整光路是最关键的一步。
《散斑干涉测微小位移》【实验目的】1、通过拍摄自由空间散斑图及成像散斑图,初步了解激光散斑现象及其特点;2.擎握应用散斑干涉全息图设计方法;3、用二次曝光散斑干涉图测量物体表面的面内位移;4、设计用二次曝光散斑图测量透明固体(玻璃)的厚度及其非均匀性。
【实验原理分析与讨论】1、散斑的形成及特征激光自散射体表面漫反射或通过一个透明散射体(加毛玻璃)时,在散射体的表面和附近空间的光场中,可以观察到或用照相记录下来一种无规分布的亮暗斑纹。
这种斑纹称为激光散斑。
它是由散射体上每个面积元发出的基元光波的干涉作用造成的。
在全息术和相干光成像系统中,散斑的存在会影响分辨率,是一种令人讨厌的有害噪声。
近年来,通过研究逐渐发现了它的一些有用的特性。
在某些新的光学系统中,散斑不再是噪声因素,而是一种有用的信息载体.激光散斑.特别是散斑照相和散斑干涉,在表面粗糙度测量、图像处理、运动分析、振动分析、眼球缺陷分析和星体度量学等科技领域中有着广泛的应用,在光学小己成为一个重要的分支。
激光散斑通常可分为空间散斑和像面散斑两类:12空间散斑:如果在散射体G 的正面距离z 的地方放置全息干板记录散斑结构,其散斑的平均直径为 1.22z ds Dλ≈,其中D 是被照亮的散射面直径。
如果在侧面接收,则散斑的平均长度2()z ls Dλ≈ 像面散斑: 像面散斑的平均直径:11.22() 1.22(1+)z ds F Dλλβ≈=式中z1(像距),D (透镜的孔径)β(横向放大率)F (相对孔径的倒数)当散射面位于无限远时,成像面与后焦面重合,散斑的平均直径为1.22() 1.22f ds F Dλλ≈= f 透镜焦距。
2、散斑干涉全息图测量面内位移的光路设计空间散斑(未加成像透镜)非平行光漫反射散斑 像面散斑(放大率>1;<1)散斑干涉光路设计 平行光 空间散斑(未加成像透镜)像面散斑(加成像透镜:放大率>1;<1)空间散斑(未加成像透镜)非平行光透射散斑 像面散斑(放大率>1;<1)平行光 空间散斑(未加成像透镜)面散斑(加成像透镜:放大率>1;<1)3.用二次曝光散斑图测量面内位移(1)反射成像散斑:二次曝光散斑图测微小位移如图是拍摄散斑图的光路布置之一,其中S 是具有光学粗糙表面的平面物体,用扩束后的激光光束照射,L 是成像透镜,H 是全息干板.置于像平面上,成像透镜L 将s 面成像于记录平面H 上,形成成像散斑,如果对浏试物体在运动前后应用二次曝光法拍摄散斑图样,并假定位移的量值大于散斑特征尺寸,那么,在同一底片上就记录了两个同样的但位置稍微错开的散斑图。
实验报告实验名称:激光散斑法测量横向微小位移实验实验时间:2015年12月18日班级:xxxx学生姓名:xxx同组人:xxx实验目的:1、观察激光散斑图,了解散斑的成因及特点。
2、掌握二次曝光法测量微小位移的原理和方法。
3、通过实际测量,验证位移量与散斑图像的关系公式。
实验仪器:导轨(800mm)、半导体激光器(650nm,25mW)、功率指示计+十二挡光探头、定时器、毛玻璃、扩束镜、准直镜、干板架、白屏、导轨滑块实验原理:激光散斑:激光自散射体的表面漫反射或通过一个透明的散射体(例如毛玻璃)后,因各点散射光或透射光干涉,在散射表面或附近的光场中可以观察到一种无规则分布的亮暗散斑。
利用激光散斑可以测量微小位移变化,具有无接触、高灵敏度等特点。
本实验中让激光通过具有粗糙表面的毛玻璃,在同一张全息干板上先后曝光两次,这样在同张激光干板上物体两幅散斑图,若物体有位移,则,两散斑图之间有一相对移动。
如果把散斑点看成圆孔,则各散斑点的移动在二次曝光散斑图上就相当于一对对“双孔”。
用激光束照射该散斑图,则会出现类似杨氏双缝干涉的图形。
λ由此可计算出微小位移。
由杨氏双缝理论:△y=ld实验内容与步骤:A、拍摄激光散斑图(1)调节图中实验装置,使得出射光束成为准直平行光。
(2)将毛玻璃片放在一维位移架上,使光斑打在毛玻璃屏中央部分。
(3)调节白屏位置,使白屏上光斑均匀。
(4)将全息干板放在白屏位置,在黑暗中,进行第一次曝光。
(5)微移全息干板位置后,进行第二次曝光。
并对全息干板进行处理,得到稳定的照片。
B、观察激光散斑图在激光器前放入拍好的散斑图,调节实验装置,使白屏上出现清晰的干涉条纹。
C、测量干涉条纹间距用刻度尺多次测量条纹间距,并在导轨上读出白屏与散斑图之间距离。
光波长λ取650nm.实验数据与分析:△y=y i5=0.9+0.85+0.8+0.85+0.85=0.84cm通过衍射条纹测得的位移d=lλ△y =0.2000×650×10−90.0084=1.5×10−5m横向位移L=0.7×1/50mm=1.4×10−5m误差η=d−LL×100%=7.1%L为一次测量量,其不确定度U L取仪器的最小精度2.0×10−5mL±U L=(1.4±2.0)×10−5m对于d,△y五次测量的不确定度公式分别用U=pn 2S x2+△仪2公式来计算,其中△仪取刻度尺的最小测量精度0.01cm,pn取1.24,S x2用贝塞尔公式s=S i−S平均23i=12,l的不确定度取仪器最小精度0.1cm,λ的不确定度取1nm。
微小位移测量实验报告一、引言微小位移测量装置是我们老师和师兄为测量空间内的一小段微米级的位移量而设计出来的测量仪器,本仪器首先应用力学原理将一个“微小位移量”作信号的初级放大,继而运用光学原理选择了可同时提供多个信息量的平面偏振光作信号传递载体,以及具有高放大倍率的石英晶体作信号转换元件。
最终,探测器接受到的信号经学生自行设计的图形处理软件输出测量结果。
但是我们在使用该测量仪器的时候,发现由于石英晶体的制造和操作上的产生的误差,会使我们测量出的结果与理论计算的结果有偏差,而且测量结果的重复性不太好,于是我们设想为这台测量仪器建立校正曲线。
通过校正曲线来提高我们测量的准确性和重复性。
二、实验过程(一)实验原理分析(1)实验仪器基本组成结构(图1)①激光器:提供光源②狭缝:控制光斑大小; 起偏器:产生线偏振光③光束优化器:提供光强分布致密、均匀、尺寸符合测试要求④转盘(载物台):放置试样的可旋转平台⑤平移台:放置晶体并可沿垂直于导轨方向作平移调节⑥检偏器:检测穿过石英晶体的光束的偏振态⑦光电倍增管:接收光信号并放大⑧计算机:控制系统的运行,将接收到的数字图像信号作处理,输出测试结果。
(2)测量原理装置是由信号输入及传递、信号初级放大、信号转换及二次放大、信号检测和图形处理装置这四大部分组成,各个部分的工作原理及结构如下:①信号传递部分考虑到迈克耳逊干涉仪是现在能精确确定长度的仪器,于是采用迈克耳逊干涉仪来给装置输入一个微小位移量,继而通过一根可在导轨上滑动的长杆及微调部件来起传递微小位移量的作用。
②信号初级放大部分运用力学原理,对输入的长度信号先作初级放大,一方面作用是提高测量的精确性,再者将放大后的光信号在传递到石英晶体上的位移比激光光束的直径要宽,从而保证输入的位移量能引起旋光角的变化。
初级放大原理如图2,杠杆装置是由固定轴4、绕轴线(过O点,垂直于纸面)旋转的轴套1和一根转动臂2组成。
轴套下端有一较小的凸点G1,G1点绕轴心O点运行的轨迹为一半径为r的圆,r=G1O。
实验十五 数字散斑测量微小位移的实验
实验目的:
1. 掌握数字散斑干涉的原理。
2. 学会根据CCD ,激光器等器件,利用计算机进行快速傅立叶变换,测量物体的微
小位移。
3. 学会分析思考并处理实验中出现的问题。
实验原理:
当一束激光照射到具有漫射特性的粗糙表面上时,在反射光的空间中用一个白色的屏去接收光总可以看到一些斑点,这就是激光散斑现象。
散斑现象是高度相干性光源照明的结果,虽然会降低全息照相时的成像质量,但由于散斑的大小、位移及运动是有规律的,它可以用来进行微小位移的检测、形变测量以及振动研究等。
传统的散斑干涉测量技术采用在同一张底片上记录物体位移前后的双曝光散斑图,并通过会聚透镜进行光学傅立叶变换得到杨氏条纹图。
随着CCD 的日益普及出现了数字散斑干涉技术,散斑图可以方便的记录在计算机中,并使用数字傅立叶变换进行处理和分析,避免了底片冲印测量的繁琐过程,可以实现方便快速的实时测量。
通过CCD 捕获被测物体位移前后的双曝光散斑图,对双曝光散斑图的任一点附近取一小块区域进行两次快速傅立叶变换,可以得到物体位移的方向和距离。
设位移前后的散斑图分别为()21,x x g i 和()2211,u x u x g itd ++,叠加得双曝光散斑图
()()()22112121,,,u x u x g x x g x x g itd i +++= (15-1)
用快速傅立叶变换对其中一小块区域进行计算,结果为一小幅杨氏条纹图。
()
()()[]()[]⎰⎰∆
+-∙+++=212211*********exp ,,,dx dx x x j u x u x g x x g G itd i ωωπωω
(15-2)
上式中,()21,ωωG 为频谱图上的谱面函数,21,ωω为谱面坐标,∆是积分域。
根据傅立叶平移原理,并假设21,u u 很小,可得双曝光散斑图相应的光强为:
()()
()()()()[]
ωπωωω
πωωωωωω
d V I d I G I g g 2cos 1,2cos ,4,2
2
12
21'2
2121+=∙=+= (15-3)
式中()21,u u d = ,()21,ωωω=
,()1≤V 是杨氏条纹的对比度。
这样,得到形成明暗
相间的杨氏条纹。
为求得杨氏条纹的密度和方位,需再进行一次快速傅立叶变换,得到
()21,ωωg I 的谱面函数,1ξ和2ξ为频谱坐标,δ为域,
()()()[]2122112121'2exp ,,ωωωξωξπωωξξδ
d d i I H g +-∙=⎰⎰ (15-4)
化简得:
()()()()221122112121',,,2,u u VH u u VH H H --++++=ξξξξξξξξ
(15-5)
此式表明谱面函数分三个部分: A. 0,021==ξξ处光晕谱是一亮点。
B.
2211,u u ==ξξ以及2211,u u -=-=ξξ处是两个对称的次亮点。
光强灰度不到晕谱一半光强,次亮点位置表示位移d
:
2
221u u u d d +=== (15-6)
次亮点连线与水平轴夹角θ即位移的方向12u tg =θ
在本实验中,用毛玻璃作为待测物体,通过CCD 分别记录毛玻璃位移前和位移后的两幅散斑图,通过计算机处理得到双曝光散斑图。
由于数字傅立叶变换的局限性,每次都只取双曝光散斑图的256×256区域进行傅立叶变换。
通过二次傅立叶变换可以得到毛玻璃位移的方向和距离。
实验器材:
He-Ne 激光器、扩束镜、准直透镜、傅里叶变换透镜、CCD (3mm ×4mm 、640×480像素)、计算机、毛玻璃(待测移动物体)、图像处理软件DSPI 。
实验光路:
H e-N e L aser
L L 1
L 2
数字散斑干涉实验光路图
实验步骤:
1.按实验光路所示搭建好光路:
1) 调节激光束平行于全息台面;
2) 在台面上选择合适的位置放置准直透镜L 1和傅里叶变换透镜L 2,使光束垂直
经过透镜的中心;
3) 在准直透镜L 1前放置扩束镜L ,使光束垂直经过其中心,前后调节其位置,
使光束经过L 1后成平行光;
4) 放上滤波器PN ,仔细调节,使其滤除杂光;
5) 在成像透镜L 2的前焦面放置待测物体毛玻璃,并且与光轴垂直; 6) 调节CCD 的位置使其正对透镜L2。
2.数字散斑干涉软件的使用
1) 运行DSPI 可执行程序,单击接通按钮由“Off ”转为“On ”,打开CCD 摄像
头。
单击格式按钮,设置摄像头分辨率为640×480,图像格式为24位RGB ; 2) 打开激光器,按DSPI 的“开始测试”按钮;
3) 先后按下“位移前”和“位移后”按钮记录被测物体位移前和位移后散斑干涉
图;
4) 在编辑框中输入x 和y 的值,设置将要在双曝光散斑干涉图上截取的小块区域
的起点;
5) 按“第一次FFT ”按钮,得到傅立叶条纹的图像,并可拖动滚动调条件对比度,
按“保存”按钮保存图像;
6) 按“第二次FFT ”按钮,得到物体移动方向和距离图像,按“保存”按钮保存
图像;
3.物体微小位移的方向二次傅立叶变换后的数字双曝光散斑图的对应关系
在不同的方向移动毛玻璃微小距离,和二次傅立叶变换后的图比较,得出图中亮点连线的方向和毛玻璃移动方向的关系;
4.确定物体微小位移的方向和距离与二次傅立叶变换后的数字双曝光散斑图的对应关系
在不同的方向移动毛玻璃微小距离,记录下移动的距离Lo,并和二次傅立叶变换后一对亮点间的距离Li(以象素点为单位)比较得出比例关系,k=Lo/Li;
5.数字散斑干涉技术测量物体的微小移动距离
把毛玻璃移动微小的距离,测量二次傅立叶变换后的散斑图上亮点的距离Li,根据Lo=k*Li,得到毛玻璃移动的实际距离;
6.第4,第5步多次测量取平均值,绘制表格填入实验数据。
思考题:
1.数字散斑测量中的被测物体微小移动距离受哪些条件的限制,本实验中能测量的最大移动距离大概是多少?
2.定性分析实际移动距离和数字图像中亮点的距离比例k的大小取决与哪些条件。