气体性质及达西定律

理想气体的性质与过程解析理想气体是指在一定温度和压力范围内，分子之间的相互作用可以忽略不计的气体。

它是理想化的模型，用来描述真实气体的一些性质和行为。

以下是关于理想气体的性质和过程的解析：性质：1.粒子间无相互作用：在理想气体中，气体分子之间的相互作用力可以忽略不计。

这意味着理想气体的压力、温度和体积只取决于其分子数，与分子之间的相互作用无关。

2.分子间的容积可以忽略不计：理想气体中，分子的体积与整个气体的体积相比可以忽略不计。

这是因为气体分子的体积相对较小，与气体分子数目相比较小时，分子之间的碰撞几乎没有。

3.分子运动速度分布均匀：理想气体中，气体分子的平均动能与温度成正比。

根据麦克斯韦速度分布律，气体分子的速度呈现高斯分布，也就是说在给定温度下，速度越快的分子数量越少。

4.气体的体积与压力成反比：根据波义耳定律，理想气体的体积和压力成反比。

当温度和分子数目保持不变时，压力增大，则气体的体积减小；压力减小，则气体的体积增大。

过程：1.等温过程：在等温过程中，理想气体的温度保持不变。

根据理想气体状态方程PV=nRT（其中P代表压力，V代表体积，n代表物质的摩尔数，R代表气体常数，T代表温度），等温过程中的压强和体积成反比。

即PV=常数。

2.等容过程：在等容过程中，理想气体的体积保持不变。

根据理想气体状态方程PV=nRT，等容过程中的压强和温度成正比。

即P/T=常数。

3.等压过程：在等压过程中，理想气体的压力保持不变。

根据理想气体状态方程PV=nRT，等压过程中的体积和温度成正比。

即V/T=常数。

4.绝热过程：在绝热过程中，理想气体不与外界交换热量。

根据绝热过程的定义，PV^γ=常数（其中γ为比热容比，γ=Cp/Cv，Cp为定压比热容，Cv为定容比热容），即压强和体积的乘积的γ次方等于常数。

总结：理想气体的性质和过程可以通过理想气体状态方程以及各种过程方程来描述。

理想气体的性质包括分子间无相互作用、分子间的容积可以忽略不计、分子速度分布均匀以及气体体积与压力成反比。

达西定律公式推导达西定律是描述流体在管道中的流动速度和管道内截面积之间的关系的定律。

此定律由达西于1883年提出。

根据达西定律，流体在管道中的流速与管道内的截面积成反比，即流量一定的情况下，管道截面积越小，流速越大。

达西定律的数学表达式为：V=(g*h*d)/(8*μ*L)其中：V是流体在管道中的流速；g是重力加速度；h是管道两端的高度差；d是管道的直径；μ是流体的动力粘度；L是管道长度。

现在我们将推导出达西定律的公式。

首先，考虑一段长度为L的水平管道，管道的截面积为A，流速为V。

由于是水平管道，可以忽略重力的影响，即g=0。

此时，管道两端的高度差h=0。

根据流体力学中的连续性方程，流体通过管道的流量恒定。

流量Q等于截面积A乘以流速V，即Q=A*V。

接下来，考虑管道中流体流动过程中，由于内壁的摩擦力，流速在管道内是不均匀的。

根据流速剖面的形状，可以假设流速在直径为d处达到最大值Vmax。

在达西定律的推导中，我们使用了以下几个假设：1.管道为水平管道，即重力g=0。

2.管道内部光滑，并且存在较小的摩擦。

3.管道的直径相对较小，以确保流速的变化不大。

根据以上假设，我们可以进行达西定律的推导。

设在其中一截面处的流速为V，该截面的半径为r，则流量Q等于该截面的截面积乘以流速，即Q=A*V。

根据流体力学的基本原理，流速和流量可以表示为流体的动力粘度μ、压力差ΔP和距离的关系。

对于其中一截面处，我们可以根据泊松方程和雷诺点定律得到以下关系：ΔP=-(8*μ*Q*L)/(π*d^4)其中π*d^4为其中一截面处的液体阻力，-(8*μ*Q*L)为压力差。

将上述两个方程合并，我们可以得到：Q*A=-(8*μ*Q*L)/(π*d^4)化简后可得：Q=-(8*μ*Q*L)/(π*d^4)*A消去-Q和Q，可得：1=-(8*μ*L)/(π*d^4)*A进一步化简，得到达西定律的公式：A=(π*d^4)/(8*μ*L)将A代入Q=A*V，可得：Q=(π*d^4*V)/(8*μ*L)这样，我们就得到了达西定律的公式。

介绍气体的特性和压力定律知识点：气体的特性和压力定律一、气体的特性1.气体的体积：气体分子间距离较大，体积可压缩，且随温度和压力的变化而变化。

2.气体的密度：气体密度较小，随温度和压力的变化而变化。

3.气体的温度：气体温度是分子热运动的量度，随分子热运动的加剧而升高。

4.气体的状态方程：理想气体状态方程为PV=nRT，其中P为气体压强，V为气体体积，n为气体物质的量，R为气体常数，T为气体温度。

二、气体的压力定律1.玻意耳定律（Boyle’s Law）：在恒温条件下，一定量的气体压强与体积成反比，即PV=常数。

2.查理定律（Charles’s Law）：在恒压条件下，一定量的气体体积与温度成正比，即V/T=常数。

3.盖·吕萨克定律（Gay-Lussac’s Law）：在恒体积条件下，一定量的气体压强与温度成正比，即P/T=常数。

4.理想气体状态方程：综合玻意耳定律、查理定律和盖·吕萨克定律，得到理想气体状态方程PV/T=nR，适用于一定量的理想气体在恒温、恒压或恒体积条件下的变化。

5.实际气体：在特定条件下，真实气体的行为与理想气体存在偏差，如范德瓦尔斯方程PV=nRT+an/Vm，其中a为吸引常数，Vm为摩尔体积。

三、气体压强与体积的关系1.绝对压强与相对压强：绝对压强是指气体对容器内壁的实际压力，相对压强是指气体压强与外界大气压的差值。

2.等温变化：在恒温条件下，气体压强与体积成反比，即PV=常数。

3.等压变化：在恒压条件下，气体体积与温度成正比，即V/T=常数。

4.等体积变化：在恒体积条件下，气体压强与温度成正比，即P/T=常数。

四、气体压强与温度的关系1.等容变化：在恒体积条件下，气体压强与温度成正比，即P/T=常数。

2.等压变化：在恒压条件下，气体体积与温度成正比，即V/T=常数。

3.等温变化：在恒温条件下，气体压强与体积成反比，即PV=常数。

五、气体压强与物质的量的关系1.等温等压变化：在恒温恒压条件下，气体物质的量与体积成正比，即n/V=常数。

甲烷性质煤是⼀种多孔介质，是天然的吸附体，与煤伴⽣的煤层⽓以吸附态、游离态、⽔溶态三种状态存在于煤体中，但是 80%～90%的煤层⽓是以吸附形态存在于煤的过渡孔和微孔的内表⾯上，形成⼀层煤层甲烷⽓薄膜。

研究煤层⽓的吸附特征，对了解煤层中煤层⽓的解吸、扩散、运移、聚集规律和阐述煤与⽡斯突出机理具有⼗分重要的意义。

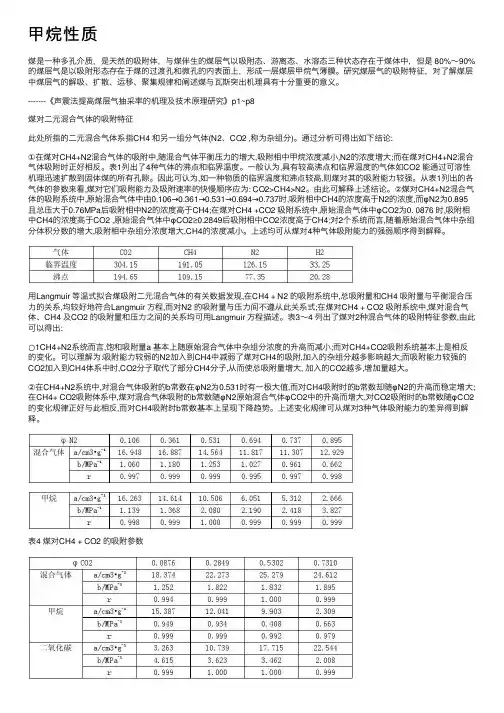
-------《声震法提⾼煤层⽓抽采率的机理及技术原理研究》p1~p8煤对⼆元混合⽓体的吸附特征此处所指的⼆元混合⽓体系指CH4 和另⼀组分⽓体(N2、CO2 ,称为杂组分)。

通过分析可得出如下结论:①在煤对CH4+N2混合⽓体的吸附中,随混合⽓体平衡压⼒的增⼤,吸附相中甲烷浓度减⼩,N2的浓度增⼤;⽽在煤对CH4+N2混合⽓体吸附时正好相反。

表1列出了4种⽓体的沸点和临界温度。

⼀般认为,具有较⾼沸点和临界温度的⽓体如CO2 能通过可溶性机理迅速扩散到固体煤的所有孔隙。

因此可认为,如⼀种物质的临界温度和沸点较⾼,则煤对其的吸附能⼒较强。

从表1列出的各⽓体的参数来看,煤对它们吸附能⼒及吸附速率的快慢顺序应为: CO2>CH4>N2。

由此可解释上述结论。

②煤对CH4+N2混合⽓体的吸附系统中,原始混合⽓体中由0.106→0.361→0.531→0.694→0.737时,吸附相中CH4的浓度⾼于N2的浓度,⽽φN2为0.895且总压⼤于0.76MPa后吸附相中N2的浓度⾼于CH4;在煤对CH4 +CO2 吸附系统中,原始混合⽓体中φCO2为0. 0876 时,吸附相中CH4的浓度⾼于CO2 ,原始混合⽓体中φCO2≥0.2849后吸附相中CO2浓度⾼于CH4;对2个系统⽽⾔,随着原始混合⽓体中杂组分体积分数的增⼤,吸附相中杂组分浓度增⼤,CH4的浓度减⼩。

上述均可从煤对4种⽓体吸附能⼒的强弱顺序得到解释。

⽤Langmuir 等温式拟合煤吸附⼆元混合⽓体的有关数据发现,在CH4 + N2 的吸附系统中,总吸附量和CH4 吸附量与平衡混合压⼒的关系,均较好地符合Langmuir ⽅程,⽽对N2 的吸附量与压⼒间不遵从此关系式;在煤对CH4 + CO2 吸附系统中,煤对混合⽓体、CH4 及CO2 的吸附量和压⼒之间的关系均可⽤Langmuir ⽅程描述。

达西定律公式k全文共四篇示例，供读者参考第一篇示例：达西定律，也称为达西公式，是描述管道内流体速度与管道内径和流体密度之间关系的一个重要定律。

达西定律得名于法国工程师亨利·菲利浦·达西（Henry Philibert Gaspard Darcy），他是19世纪著名的水利工程师、地质学家和物理学家。

达西定律在流体力学和管道工程中具有广泛的应用，为工程设计和实践提供了重要的理论支持。

在流体力学中，流体的运动状态可以通过流体速度和流体压力等参数来描述。

对于管道内的流体运动，其速度与管道内径、流体密度、流体粘度等因素有着密切的关系。

达西定律描述了管道内流体速度与管道内径、流体密度之间的定量关系，为工程师们计算管道内流体速度提供了重要参考数据。

根据达西定律的公式k，管道内流体速度v与管道内径D和流体密度ρ之间的关系可以表示为：v = k√(RS/ρ)v代表流体速度，D代表管道内径，ρ代表流体密度，k是一个常数，RS是管道的雷诺数。

根据这个公式，我们可以看出，流体速度与管道内径的平方根成反比，与流体密度成正比。

这个公式不仅可以帮助工程师们计算管道内流体速度，还可以帮助他们进行管道设计和优化。

达西定律公式k的推导过程比较复杂，需要考虑流体力学和物理学的知识。

在推导公式k的过程中，工程师们需要考虑管道内流体的黏性和流态特性，雷诺数的影响等因素。

通过合理的推导和分析，工程师们可以得到关于管道内流体速度的精确计算公式，为工程设计和实际应用提供了有力的支持。

达西定律公式k在管道工程领域具有广泛的应用价值。

在城市供水、排水系统、化工工程、石油管道等领域，工程师们都需要依靠达西定律公式k来计算管道内流体速度，从而确保管道系统的正常运行和安全性。

通过合理地使用达西定律公式k，工程师们可以优化管道设计，提高系统效率，并减少能源消耗和运行成本。

达西定律公式k是管道工程领域中一个非常重要的理论工具，它帮助工程师们理解管道内流体速度与管道内径、流体密度之间的关系，为工程设计和实践提供了坚实的理论基础。

达西定律概念
达西定律（Darcy's law）是描述流体在多孔介质中渗流的经典
定律，由法国工程师亨利·达西（Henry Darcy）于1856年提出。

该定律表明，在渗透率恒定、流体为单相不可压缩流体且遵循牛顿流体力学的情况下，单位时间内通过多孔介质的流体流量与渗透力的关系是线性的。

达西定律可以用如下的公式表示：
Q = -KA∇P
其中，Q表示单位时间内通过多孔介质的流体流量，K表示渗
透率，A表示流体流动的截面积，∇P表示流体流动方向上的
压力变化。

达西定律在地下水流动、石油工程、土壤水分运移等领域都有广泛的应用。

它是渗流理论的基础，也是研究渗流现象和设计工程的重要工具。

有关气体知识点总结1. 气体的性质1.1 可压缩性气体是一种具有可压缩性的物质状态，这是与液体和固体不同的重要特征。

由于气体分子之间的间隔非常大，因此当气体受到外压时，其分子间的间隙可以被进一步缩小，使得气体的体积变小。

这就是气体的可压缩性，而液体和固体则因分子排列方式的紧密而导致了不同的性质。

1.2 压强和体积气体的性质可以通过压强和体积来描述。

压强是单位面积上所受的力，通常用P表示，单位为帕斯卡(Pa)。

气体的体积则是描述气体空间的大小，通常用V表示，单位为立方米(m³)。

理想气体状态方程PV=nRT中的P和V即分别代表了压强和体积，其中n为气体的摩尔数，R为气体常数，T为气体的绝对温度。

2. 理想气体和真实气体理想气体是一种理想化的气体状态，在此条件下气体分子之间不存在相互作用，分子体积可以忽略不计。

在低温、高压、分子体积与分子间引力吸引相对所占比例较大等情况下，理想气体的假设不再成立，因此实际气体在这些情况下将呈现出与理想气体不同的性质，称之为真实气体。

3. 气体状态与状态方程气体的状态变化可以通过温度、压强、体积这三个基本参数来描述。

根据理想气体状态方程PV=nRT来描述气体状态，其中P为气体的压强，V为气体的体积，n为气体的摩尔数，R为气体常数，T为气体的绝对温度。

4. 气体的扩散和扩散率气体分子具有自由扩散的能力，当气体分子遇到空隙时，它会向四周扩散。

扩散速率受温度、压强、分子质量等因素的影响。

根据格雷厄姆定律，气体的扩散速率与分子质量成反比，扩散速率与根号下分子质量成正比。

5. 气体的溶解气体可以溶解在液体中，溶解的程度对溶解度、温度、压强等因素有较大影响。

亨利定律和拉瓦定律分别描述了气体溶解度和气体分压与溶解度之间的关系。

6. 气体的化学性质气体也具有一系列的化学性质，其中以氧气、氮气、氯气、氢气等为典型代表。

气体可以发生燃烧反应、氧化还原反应、及与其他物质进行反应等。

高三物理气体选修知识点在高三物理学习中，气体是一个重要的知识点。

掌握气体的性质、状态方程、分子运动和热力学过程等方面的知识，对于理解物质的宏观特性以及解决实际问题具有重要意义。

本文将介绍高三物理气体选修知识点，帮助同学们更好地掌握这一部分内容。

一、气体的性质在研究气体的性质时，常用的参数有压力、温度和体积。

压力是气体对容器壁的作用力，可用于描述气体的强弱程度；温度则与气体的分子平均动能直接相关；体积是气体所占据的空间大小。

二、状态方程气体的状态方程描述了气体的状态与压力、温度以及体积之间的关系。

理想气体状态方程可以表示为PV=nRT，其中P为气体的压力，V为气体的体积，n为气体的物质量，R为气体常数，T为气体的温度。

对于理想气体，该状态方程成立；而对于实际气体，可能需要考虑修正。

三、分子运动气体的性质与其中分子的运动方式密切相关。

分子在气体中以高速运动，并作无规则的碰撞。

分子间的碰撞会导致气体的压强，而分子运动的速度与温度直接相关。

分子运动的平均自由程与气体分子数量和体积之间有关，可用于描述气体的稀薄程度。

四、热力学过程热力学过程是气体学习的重点之一，主要包括等温过程、绝热过程、等容过程和等压过程。

在等温过程中，气体的温度保持不变，体积和压力呈反比关系；绝热过程中，气体无法与外界交换热量，体积和压力呈反比关系；等容过程中，体积保持不变，温度和压力呈正比关系；等压过程中，压力保持不变，温度和体积呈正比关系。

五、理想气体与实际气体理想气体是用来简化描述气体行为的模型，其中假设气体分子无体积、无吸引力和无相互作用。

实际气体则考虑了分子间的相互作用和体积，其状态方程需要进行修正，例如范德瓦尔斯方程和爱因斯坦方程。

六、气体的溶解度气体在液体中的溶解度也是气体学习的一部分。

溶解度与气体分压和温度成正比，与液体的性质有关。

亨利定律描述了气体在线性温度范围内的溶解度与分压的关系。

通过对以上知识点的学习，我们能够更好地理解气体的性质和行为规律，掌握气体的状态方程以及热力学过程。

达西定律表达式及其物理意义(1)达西定律:流量等于过水断面(垂直于渗流方向的含水层截面,包括空隙和颗粒骨架所占的空间)的面积乘以水力坡度再乘以渗透系数。

Q=Kωh/L= KωIV=KI其中:Q—渗透流量(出口处流量,即为通过砂柱各断面的流量);ω—过水断面(实验中相当于砂柱横断面积);h—水头损失(h=H1-H2,即上下游过水断面的水头差);I—水力梯(坡)度(相当于h/L,即水头差除以渗透途径);K—渗透系数;V—渗透流速。

(2)公式各项的物理意义①渗流速度(虚拟流速)在渗流中把复杂的地下水的运动断面简化成一个连续的过水断面,而这个断面上的流量与实际流量相等,通过试验,出口的流量是实测的,是实际流量,这个实际流量并不象地表水那样占满整个过水断面,仅仅是从空隙中通过,而孔隙的面积小于实际地质断面面积,即渗透流速小于实际流速,说明渗透流速不是实际流速,而小于实际流速,即实际允许水通过的面积小于地质断面面积。

Q=ω’u=ωV,又ω’=ωne,有孔隙平均流速: u=V/ ne②水力坡度沿渗透途径的水头损失与相应的渗透途径长度的比值,说明有水力坡度是地下水运动的必要条件,是地下水运动的驱动力。

水力坡度可以理解为单位长度上为克服摩擦阻力所消耗的机械能。

水力坡度大,在平面图上等水位线越密,否则则反,在剖面图中,水位线越陡,反之则反。

③渗透系数从渗透流速等于渗透系数乘以水力坡度可知,水力坡度是无因次的,而渗透流速的量纲是速度的量纲,故渗透系数也是一个速度量纲,当水力坡度等于1时,渗透系数在数值上等于渗透速度。

虽然两者均具有速度的量纲,但它们是有区别的,应引起注意。

水通过多孔介质的速度同水力梯度的大小及介质的渗透性能成正比。

反映水在岩土孔隙中渗流规律的实验定律。

由法国水力学家 H.-P.-G.达西在1852～1855年通过大量实验得出。

其表达式为：Q=KFh/L式中Q为单位时间渗流量，F为过水断面，h为总水头损失，L为渗流路径长度，I=h/L为水力坡度，K为渗透系数。

气体的性质玻意耳定律的推导气体的性质与玻意耳定律的推导气体是一种物态，在自由空间中能够自由移动和扩散。

本文将通过推导玻意耳定律，来探究气体的性质和行为规律。

一、气体的性质气体具有以下几个主要的性质：1. 压强：气体对容器壁施加的压力称为压强，通常用P表示，单位为帕斯卡（Pa）。

2. 体积：气体所占据的空间称为体积，通常用V表示，单位为立方米（m³）。

3. 温度：气体的热度大小称为温度，通常用T表示，单位为开尔文（K）。

4. 分子速率：气体中分子的运动速度，与温度有关，分子速率越高，温度越高。

5. 分子间的作用力：气体分子之间的相互作用力较弱，通常可以忽略。

二、玻意耳定律的推导玻意耳定律是描述气体行为的基本规律，它建立了气体的压强、体积和温度之间的数学关系，表达为：P * V = n * R * T。

1. 假设在恒温下，将气体体积从V₁变化到V₂，压强由P₁变化到P₂。

2. 假设气体分子数量为n，R为气体常数，温度保持不变，即温度为T。

3. 根据分子的运动理论，气体分子与容器壁碰撞时会产生压强，且碰撞的次数与分子数量成正比。

4. 假设在单位时间内，每个分子与容器壁碰撞的次数为Z，那么总的压强P即为每次碰撞产生的压强乘以碰撞次数，即P = Z * F（F为单位面积上受到的压力）。

5. 由于气体分子之间的作用力较小，所以气体分子与容器壁碰撞后会立即脱离，即每次碰撞产生的压强相互独立。

6. 根据动能定理，每个分子的动能与速率的平方成正比，即K = 1/2 * m * v²（m为分子质量，v为速率）。

7. 由于动能定理和分子速率与温度成正比，所以每个分子与容器壁碰撞产生的压强与温度成正比。

8. 根据以上推导可得，P ∝ T。

9. 根据波义耳定律中PV = constant的关系，可得P₁ * V₁ = P₂ * V₂。

通过以上的推导过程，我们得到了玻意耳定律的数学表达式P * V = n * R * T。

空气渗透率空气渗透率测试是让清洁干燥的空气在合适的压差下通过滤板，测量其压差和流速，计算出样品的渗透率。

建议一般情况下采用约980Pa的压差，以保证空气在层流条件下通过滤板。

由于绝对渗透率是与流体性质无关而仅与岩石本身孔隙结构有关的物理参数，因此生产中使用的绝对渗透率一般是用的空气渗透率测试来测定。

测定原理渗透率的大小表示了多孔介质，让流体通过能力的大小，其单位是平方微米（达西）或毫平方微米（毫达西）。

粘度为1mPa·s的液体在0.1MPa（1绝对大气压）压力作用下通过截面积为1cm、长度为1cm的岩心，液体的流量为1cm/S 时，其渗透率为1um。

气体在多孔介质中流动时，由气体的一维稳定渗流达西定律可得到下面的公式：达西定律的应用必须满足以下三点：1）流体流动是层流。

2）流体与岩石无反应。

3）孔隙空间被单相流体完全饱和。

上式中的气体渗透率是绝对渗透率，是岩心自身的性质，取决于岩石的孔隙结构，在满足上述三点的条件下，岩心的绝对渗透率与通过的流体性质无关。

在实验室测定时，通常用空气作为通过岩心的介质，因此，岩心的绝对渗透率又称作空气渗透率。

其测定原理是气体的一维稳宗流达西定律。

小柱塞岩样测定方法流量计法①测定流程流程包括三部分：1）压力计量部分：压力表、“C”值表、水银压力计等；2）流速计量部分：节流器、皂膜流速计、毛管流量计、孔板流量计等；3）岩心室：赫斯勒型、范彻尔型或圆盘型岩心夹持器。

②测定步骤1）岩心尺寸的测量：对规则岩样，可用卡尺量出；对不规则样品，如果两端面平行，可以测出总体积和长度，计算出平均横截面积。

2）将待测样品装入岩心夹持器（注意岩样的上、下方向）。

3）测量干燥气体通过岩样的气体流速，记录流速及岩心上、下流的压力，或记录“C”值、节流器标定流量和测量回压水柱高度。

③注意事项1）仪器应经常用标准样进行检查、校正；2）岩样在测定前应进行全面检查，去掉有人为裂缝的样品；3）要保证测样绝对密封；4）需用密封材料密封的样品，密封材料渗入岩样的深度不得超过一个砂粒；5）严防污染岩样，特别是两个端面；6）压力稳定后才能记录读数。

达西定律公式单位达西定律是描述流体在多孔介质中流动的一个重要定律。

咱们先来瞅瞅这个定律的公式：Q = KA（Δh/L）。

这里的 Q 表示流量，单位是立方米每秒（m³/s）；K 是渗透系数，单位是米每秒（m/s）；A 是过水断面面积，单位是平方米（m²）；Δh 是水头损失，单位是米（m）；L 是渗透途径的长度，单位是米（m）。

我记得有一次在给学生们讲解达西定律的时候，发生了一件特别有趣的事儿。

那是一个阳光明媚的上午，我像往常一样走进教室，准备给大家上这堂关于达西定律的课。

我在黑板上写下了达西定律的公式，然后开始解释每个变量的含义和单位。

当我讲到流量 Q 的单位是立方米每秒的时候，有个调皮的学生突然举手说：“老师，这立方米每秒感觉好抽象啊，能不能举个例子让我们更好理解？”我想了想，灵机一动，说道：“同学们，想象一下，咱们学校的游泳池，假设它是一个长方体，长 25 米，宽 10 米，平均水深 2 米。

如果要在 1 秒钟内把这个游泳池的水全部换一遍，那这个水流的速度就是流量 Q 啦，大约就是 500 立方米每秒。

”同学们听了，眼睛都瞪得大大的，好像一下子明白了。

接着，我们继续探讨渗透系数 K 的单位米每秒。

为了让大家更直观地感受，我拿出了一块海绵和一杯水，做了一个小实验。

我把海绵平放在桌子上，然后慢慢地把水倒在海绵的一端，让水渗透过去。

同学们都紧紧地盯着海绵，看着水慢慢地渗透。

我告诉他们，海绵就像是多孔介质，水在海绵中渗透的速度就和渗透系数 K 有关。

在讲解过水断面面积 A 的单位平方米时，我让同学们分组讨论，想想生活中哪些地方能看到不同大小的过水断面。

有的小组说下水道的管口，有的说河流的横截面。

大家讨论得热火朝天，课堂气氛特别活跃。

而讲到水头损失Δh 的单位米，我给大家讲了一个故事。

我说：“假设我们要把水从一楼抽到十楼，水在上升的过程中，压力会逐渐变小，就好像水在爬山一样，越往上爬就越累，这个压力的减小量就相当于水头损失。

达西定律流速-概述说明以及解释1.引言1.1 概述概述达西定律（Darcy's Law）是描述渗流运动的基本规律之一，是在地下水领域中被广泛应用的理论模型。

它是由法国工程师亨利·达西（Henry Darcy）在19世纪中期提出的，用于解析和预测地下水在多孔介质中的流动行为。

达西定律基于达西流动实验的观察结果，它指出了渗流速度与渗透系数、梯度和孔隙度之间的关系。

在达西定律中，渗透系数反映了岩石或土壤中水分传导的能力，梯度表示了水力头（水势）随空间变化的速率，而孔隙度则是指多孔介质中包含的空隙的比例。

达西定律的公式表达为：流速=渗透系数×梯度。

根据达西定律，渗流速度正比于渗透系数和水力头梯度之间的乘积。

这意味着当渗透系数增加或者水力头梯度增大时，渗流速度也会增加。

达西定律的应用领域非常广泛。

在地下水领域，它被用于研究地下水的流动和传输规律，预测地下水的补给和排泄量，评估地下水资源的可持续利用性。

而在土力学和地质工程中，达西定律则被用于分析土壤和岩石的渗流行为，帮助设计和建造地下工程结构，例如隧道、堤坝和地下储层。

然而，达西定律也存在一些局限性。

它基于一些理想假设，例如认为渗透系数是恒定的，不考虑渗透介质的非均质性和非稳定性。

因此，在实际应用中，需要结合实际情况和其他模型进行定量分析和预测。

总之，达西定律作为描述渗流规律的基础理论，对于地下水和地下工程领域的研究和应用具有重要意义。

通过深入研究和进一步探索，可以推动达西定律在实践中的应用，并促进地下水资源的合理管理和地下工程的安全可靠建设。

1.2文章结构1.2 文章结构本文将按照以下结构进行展开讨论达西定律的流速问题：第一部分是引言，将以概述的方式介绍达西定律流速的背景和相关概念。

我们将明确文章的目标和意义，为读者提供对整篇文章的整体了解。

第二部分是正文，将分为三个小节来探讨达西定律的定义和原理、应用领域以及局限性。

在2.1小节中，我们将详细介绍达西定律的定义和原理，解释其中的数学表达式和物理概念，并说明其在理解流体流动中的重要性。

高三物理气体的性质知识点高三物理知识点总
结
气体的性质 1.气体的状态参量：
温度：宏观上，物体的冷热程度;微观上，物体内部分子无规则运动的剧烈程度的标志，热力学温度与摄氏温度关系：
T=t+273 {T:热力学温度(K)，t:摄氏温度(℃)｝
体积V：气体分子所能占据的空间，单位换算：
1m3=103L=106mL
压强p：单位面积上，大量气体分子频繁撞击器壁而产生持续、均匀的压力，标准大气压：
1atm=1.013105Pa=76cmHg(1Pa=1N/m2)2.气体分子运动的特点：分子间空隙大;除了碰撞的瞬间外，相互作用力微弱;分子运动速率很大3.理想气体的状态方程：p1V1/T1=p2V2/T2 {PV/T=恒量，T 为热力学温度(K)｝
注:
(1)理想气体的内能与理想气体的体积无关,与温度和物质的量有关;
(2)公式3成立条均为一定质量的理想气体，使用公式时要注意温度的单位，t为摄氏温度(℃)，而T为热力学温度(K)。

第 1 页共 1 页。

化学理想气体知识点总结一、理想气体的特性理想气体是指在大多数情况下，气体分子之间几乎不受相互作用的影响，可以用理想气体方程式描述其状态。

理想气体的特性包括以下几个方面：1. 无相互作用：理想气体分子之间几乎没有相互作用，分子之间的吸引力和斥力可以忽略不计。

2. 分子体积忽略不计：理想气体分子的体积可以忽略不计，与容器的体积相比可以忽略不计。

3. 分子间的平均动能与温度成正比：理想气体分子的平均动能与温度成正比，即温度越高，分子的平均动能越大。

4. 气体分子运动呈无规则直线运动：理想气体分子在运动时呈无规则直线运动，在碰撞时完全弹性碰撞。

以上这些特性使得理想气体具有简单的物理性质，使得理想气体方程式可以描述其状态，并为化学研究和应用提供了理论基础。

二、理想气体的状态方程理想气体的状态方程是描述理想气体状态的基本公式，可以用来计算气体的压力、体积、温度等物理量之间的关系。

理想气体方程式可以用三种不同的形式来表示，分别为：1. 体积-压力-温度关系：PV = nRT式中，P表示气体的压力，V表示气体的体积，n表示气体的摩尔数，R表示气体常数，T 表示气体的温度。

2. 摩尔体积-压力-温度关系：PV = NkT式中，P表示气体的压力，V表示气体的摩尔体积，N表示气体的分子数，k表示玻尔兹曼常数，T表示气体的温度。

3. 分子速率-温度关系：v = (3kT/m)^0.5式中，v表示气体分子的速率，k表示玻尔兹曼常数，T表示气体的温度，m表示气体分子的质量。

这三种形式的理想气体方程式可以根据不同的实际情况来选择使用，便于求解不同的气体状态问题。

三、理想气体的性质理想气体的性质是指理想气体在不同条件下的状态性质，包括压缩性、可压缩性和等温过程等。

1. 压缩性：在一定外力的作用下，气体可以发生压缩变化，其压缩性可以用压缩系数来描述。

理想气体的压缩系数为0，即在一定外力作用下，理想气体的体积不会发生变化。

2. 可压缩性：理想气体在受到外力作用时，体积会发生变化，即理想气体具有可压缩性。

达西定律遵守的质量守恒定律
牛顿定律（质量守恒定律）是物理学中最重要的一条经典定律，它声明物质的数量是不变的，当物体相互发生作用的时候，其中物质的数量也是不变的。

也就是说，物质不会因为发生作用而消失。

牛顿定律被称为质量守恒定律，因为它的基本原理确实是质量的守恒。

牛顿定律最早由英国物理学家牛顿发现，他在他的著名著作《原子力学》中介绍了它。

他在书中指出，物质不会因为发生作用而消失，只有当物质产生另外一种形式，才可能发生转化。

牛顿定律被用于各种物理气体理论，它可以用来解释发生在物体上的种种变化，比如热力学的热能和动能的转化。

随着物理学的发展，牛顿定律的应用也越来越广泛。

比如在电力学中，它被用来解释复合电路中的质量守恒。

在气象学中，它被应用来解释物质的蒸发和凝结的原理。

在化学反应中，牛顿定律也被广泛地使用，以确定化学反应中物质的净变化。

实际上，任何一种物理反应最终都可以归结为牛顿定律。

这就是为什么牛顿定律被称为宇宙的基本定律，因为它涵盖了物质数量的守恒性。

只有把物质的数量守恒了，我们才能用物理的方法正确的解释宇宙的种种变化。

随着自然科学的发展，越来越多的科学现象都可以归结到这条定
律。

从力学到热学，从化学到气象学，从数学到物理学，牛顿定律在各个学科中都有重要的地位。

牛顿定律确保了物质实体的守恒最终能够支持宇宙变化的整个过程。

总之，牛顿定律是宇宙秩序保持所必不可少的定律之一。

该定律明确了质量守恒定律，即物质数量不能因发生变化而消失。

在宇宙的范围内，只有确保质量的守恒性，才能真正解释宇宙的本性和变化现象。