2021届高三数学之函数与导数(文理通用)专题09极值点偏移(二)
- 格式:docx
- 大小:1.07 MB
- 文档页数:18

极值点的“偏移”问题一、极值点“偏移”图示(左右对称,无偏移,如二次函数;若f(x1)=f(x2),则x1+x2=2x0)(左陡右缓,极值点向左偏移;若f(x1)=f(x2),则x1+x2>2x0)(左缓右陡,极值点向右偏移;若f(x1)=f(x2),则x1+x2<2x0)二、极值点偏移问题的结论不一定总是x1+x2>(<)2x0,也可能是x1x2>(<)x20.三、解题策略:对称化构造法;双变元不等式问题解法一【例1】已知函数f(x)=x e-x 如果x1≠x2,且f(x1)=f(x2),证明:x1+x2>2.1.设函数f(x)=(x−2)e x+a(x−1)2有两个零点.(1)求a的取值范围;(2)设x1,x2是f(x)的两个零点,证明:x1+x2<2.2.设函数 f(x)=ln x−ax(a>0),且实数m使得方程f(x)=m有两个不等实根x1,x2,其中x1<x2.求证:(1)0<x1<1a<x2;(2)x1+x22>1a.3.设函数f(x)=ln xx,且实数m使得方程f(x)=m有两个不等实根x1,x2,其中x1<x2.求证:(1)0<x1<e<x2;(2)x1+x22>e;(3)1x1+1x2>2ⅇ.4.已知函数f(x)=e x-ax有两个不同的零点x1,x2,其极值点为x0. (1)求a的取值范围;(2)求证:x1+x2<2x0;(3)求证:x1+x2>2;(4)求证:x1x2<1.5. 设函数f(x)=e x−ax,其中a>e,(1)求证:函数f(x)有且仅有两个零点x1,x2,且0<x1<1<x2;(2)对于(1)中的x1,x2,求证:f′(x1)+f′(x2)>0.6.已知函数f(x)=x ln x-x,两相异正实数x1,x2满足f(x1)=f(x2).求证:x1+x2>2.总结:用对称化构造的方法解决极值点偏移问题分为以下三步:(1)求导,获得f(x)的单调性,极值情况,作出f(x)的图象,由f(x1)=f(x2)得x1,x2的取值范围(数形结合);(2)构造辅助函数,对结论x1+x2>(<)2x00,构造F(x)=f(x)-f(2x0-x);对结论x1x2>(<)x20,构造F(x)=f(x)-f⎝⎛⎭⎫x20x,求导,限定范围(x1或x2的范围),判定符号,获得不等式;(3)代入x1(或x2),利用f(x1)=f(x2)及f(x)的单调性证明最终结论.双变元不等式问题解法二【例2】(2020·重庆调研二)已知函数f(x)=x ln x,g(x)=12mx2+x.设F(x)=f(x)-g(x),已知F(x)在(0,+∞)上存在两个极值点x1,x2,且x1<x2,求证:x1x2>e2(其中e为自然对数的底数).1.设A(x1,y1),B(x2,y2)是函数f(x)=ax2+(1−2a)x−ln x图像 C上不同两点,M为线段AB的中点,过M作x轴的垂线交曲线C于N点.试问:曲线C在点N处的切线是否平行于直线AB?2.设函数f(x)=x2−(a−2)x−a ln x,a>0.若方程f(x)=m有两个不等实根x1,x2,求证:f′(x1+x22)>0.3.设函数f(x)=x ln x,且实数m使得方程f(x)=m有两个不等实根x1,x2,求证:x1x2<1ⅇ2.4.设函数f(x)=ln xx,且实数m使得方程f(x)=m有两个不等实根x1,x2,求证:f′(x1)+f′(x2)>0. 5.设函数f(x)=e x−ax+a有两个零点x1,x2,求证:x1x2<x1+x2.6. 已知函数f(x)=ln x和g(x)=ax,若存在两个实数x1,x2,且x1≠x2,满足f(x1)=g(x1),f(x2)=g(x2),求证:x1x2>e2.。


导数压轴题分类(2)---极值点偏移问题极值点偏移问题常见的处理方法有⑴构造一元差函数Fx f x f 2x 0 x 或者F x f x o x f x o x 。
其中x o 为函数y f x 的极值点。
⑵利用对数平均不等式。
•、ab-—b -—b 。
⑶变换主元等方法。
In a In b 2任务一、完成下面问题,总结极值点偏移问题的解决方法。
2 21 设函数 f(x) a In x x ax (a R)(1)试讨论函数f (x)的单调性;a 21nx x 2 ax 可知 2x 2 ax a 2 (2x a)(x a)x x① 若a 0时,当 x (0, a)时,f (x)0 ,函数f (x)单调递减,当 x (a, )时,f (x) 0,函数f (x)单调递增;② 若a 0时,当 f (X) 2x 0在x (0,)内恒成立,函数f (x)单调递增;③ 若a 0时,当 x (0,a)时,f (X )0 ,函数f (x)单调递减, 因为函数f(x)的定义域为(0,),所以2 f (x)0,函数f (x)单调递增;当)时,((2) f (x) m 有两解捲必(论x 2),求证:x-i x 2 2a .解析:(1)由f(x)a 2f (x)2x axa 2,(2)要证 X i X 2 2a , 只需证 a 22 a 2xg(x) f (x)为增函数。
只需证: f (X ^jX1) f (a)0,即证2- N +X 2 a 0 (*)x , x 2 a又 a 21n X i X i 2ax i2 2m, a In X 2 X 2 ax 2 m,两式相减整理得:2x a,则 g (x)g(x) (x)x2a 2x , +x 2 aln x 1 ln x 2 1 2(x 1ix x 2a)a0,把丄(x 1aX 2 a) ln x ( xlnX 2 代入(*) X 2式,即证:x 1 x 22ln x (lnx2o 化为2(竺1)=t 即证:2(t 1) lnt 0x2ln^10,令冬x-i x 2x X 2生1xx t 1x令(t ) 2(t 1) ln t(0 t1),则⑴4 1 (t 1)2卜ot 21t 1t t1 t所以⑴为减函数,⑴(1)综上得:原不等式得证。
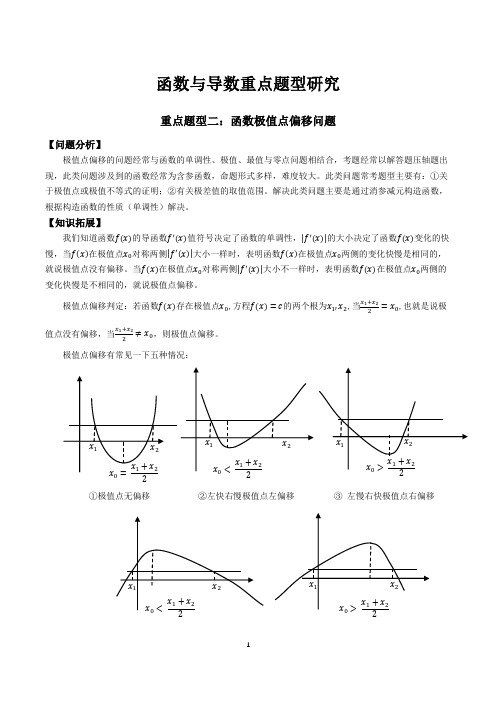
函数与导数重点题型研究重点题型二:函数极值点偏移问题【问题分析】极值点偏移的问题经常与函数的单调性、极值、最值与零点问题相结合,考题经常以解答题压轴题出现,此类问题涉及到的函数经常为含参函数,命题形式多样,难度较大。
此类问题常考题型主要有:①关于极值点或极值不等式的证明;②有关极差值的取值范围。
解决此类问题主要是通过消参减元构造函数,根据构造函数的性质(单调性)解决。
【知识拓展】我们知道函数f(x)的导函数f′(x)值符号决定了函数的单调性,|f′(x)|的大小决定了函数f(x)变化的快慢,当f(x)在极值点x0对称两侧|f′(x)|大小一样时,表明函数f(x)在极值点x0两侧的变化快慢是相同的,就说极值点没有偏移。
当f(x)在极值点x0对称两侧|f′(x)|大小不一样时,表明函数f(x)在极值点x0两侧的变化快慢是不相同的,就说极值点偏移。
极值点偏移判定:若函数f(x)存在极值点x0,方程f(x)=c的两个根为x1,x2,当x1+x22=x0,也就是说极值点没有偏移,当x1+x22≠x0,则极值点偏移。
极值点偏移有常见一下五种情况:①极值点无偏移②左快右慢极值点左偏移③左慢右快极值点右偏移x1x2x0>x1+x22x1x2x0=x1+x22x1x2x0<x1+x22x1x2x0<x1+x22x1x2x0>x1+x22④左快右慢极值点左偏移⑤左慢右快极值点右偏移口诀:谁陡向谁偏,左偏小,右偏大.【命题形式】极值点偏移问题常见的考题形式:(1)若函数f(x)存在两个零点x1,x2且x1≠x2,求证x1+x2>2x0或x1+x2<2x0(x0为函数f(x)的极值点)(2)若函数f(x)存在x1,x2且x1≠x2,使得f(x1)=f(x2),求证x1+x2>2x0或x1+x2<2x0(x0为函数f(x)的极值点)(3)若函数f(x)=c的有两个不同的根为x1,x2,求证x1+x2>2x0或x1+x2<2x0(x0为函数f(x)的极值点)(4)若函数f(x)存在两个零点x1,x2且x1≠x2,求证f′(x1+x22)≥0或f′(x1+x22)≤0.(5)若函数f(x)存在x1,x2且x1≠x2,使得f(x1)=f(x2), 求证f′(x1+x22)≥0或f′(x1+x22)≤0.【解题策略】解决极值点偏移问题主要有以下方法:(1)构造函数法:根据极值点x0构造对称函数F(x)= f(x0+x)−f(x0−x)或F(x)=f(x)−f(2x0−x),根据F(x)的正负,可以判断极值点的偏移情况,或根据F(x)单调性判断.(2)比较大小:根据函数f(x)单调性比较f(x0+x)与f(x0−x)或者 f(x)与f(2x0−x)的大小,进而得出所证结果(x0为函数f(x)的极值点).(3)证明f′(x1+x22)的符号问题,比较x1+x22与x0之间的大小,即可得出x1+x22所在的单调区间,进而得出f′(x1+x22)的正负.(4)消参减元:根据两点x1,x2之间的关系,利用简单运算,化简或转化所求问题,减少变量个数,在构造相应函数求解.【典例赏析】例一:已知函数f(x)=e x−2x−1.(1)求f(x)的单调区间;(2)若存在x1<ln2<x2,使得f(x1)=f(x2),证明:x1+x2<2ln2.试题分析:由已知导函数f′(x)=e x−2, f(x)的极值点为 x=ln2.第(1)问,很容易解决。

极值点偏移是高中数学中的一个重要概念,也是学生们比较头疼的一个知识点。
在解决数学问题时,我们经常会遇到一些与极值点有关的题型,比如函数的极值问题、优化问题等。
而在解决这些问题时,极值点偏移方法是一种非常实用的解题技巧。
本文将从四种题型出发,对极值点偏移方法进行详细解析,并结合具体例题进行说明。
1. 函数的极值问题函数的极值问题是高中数学中的一个重要内容。
在解决这类问题时,我们常常会用到导数的概念,来求函数的极值点。
但有些情况下,我们可以通过极值点偏移方法更快地得到函数的极值点。
比如对于一些简单的函数,通过极值点的平移和对称性,可以用更简洁的方法求得函数的极值点。
举例说明:已知函数 $f(x)=x^3-3x^2+2$,求 $f(x)$ 的极值点。
解:求导得 $f'(x)=3x^2-6x$。
令导数为零,得到 $x=0$ 或 $x=2$。
根据导数的符号,可知 $x=0$ 是极小值点,$x=2$ 是极大值点。
但通过极值点偏移方法,我们可以发现,当 $x=0$ 时,$f(x)=2$;而当$x=2$ 时,$f(x)=2$。
也就是说,极小值点 $x=0$ 对应的函数值和极大值点 $x=2$ 对应的函数值相等。
这就是极值点偏移的思想。
2. 优化问题优化问题是数学建模中常见的类型之一,也是考察学生综合运用数学知识解决实际问题的一种形式。
当我们遇到优化问题时,常常需要求解函数的极值点。
而极值点偏移方法可以帮助我们更快地找到函数的极值点,从而解决优化问题。
举例说明:一块长为20厘米的铁皮,可以做成一个底面积为 $x cm^2$ 的正方形盒子和一个底面积为 $y cm^2$ 的开口放平盒子,求怎样分割这块铁皮才能使总体积最大。
解:设正方形盒子的边长为 $a$,开口朝下的放平矩形盒子的底边长为 $b$,高为 $h$。
则根据题意可知,$b=a+2h$,且 $x=a^2$,$y=bh$。
问题转化为求 $x+y$ 的最大值。

(完整word版)⾼中数学极值点偏移问题极值点偏移问题沈阳市第⼗⼀中学数学组:赵拥权⼀:极值点偏移(俗称峰⾕偏)问题的定义对于可导函数y=f(x)在区间(a,b)上只有⼀个极⼤(⼩)值点x0,⽅程f(x)=0(f(x)=m)的解分别为x1,x2且a 若x1+x22≠x0,,则称函数f(x)在区间(a,b)上极值点x0偏移;(1)x1+x22>x0,则称函数f(x)在区间(a,b)上极值点x0左偏移;(2)x1+x22⼆:极值点偏移的判定定理对于可导函数y=f(x)在区间(a,b)上只有⼀个极⼤(⼩)值点x0,⽅程f(x)=0(f(x)=m)的解分别为x1,x2且a (1)若f(x1)2(2)若f(x1)2>x0即函数f(x)在区间上(a,b)极⼩值点x0左偏;(即⾕偏左)(3)若f(x1)>f(2x0?x2)则x1+x22>x0即函数f(x)在区间上(a,b)极⼤值点x0左偏;(即峰偏左)(4)若f(x1)>f(2x0?x2)则x1+x22拓展:1)若)()(x b f x a f -=+,则)(x f 的图象关于直线2ba x +=①f(x)在(0,a)递增,在(a,2a)递减,且f(a -x)<(>)f(a+x)(f(x)<(>)f(2a -x)) ②f(x)在(0,a)递减,在(a,2a)递增,且f(a -x)>(<)f(x+a)(f(x)> (<)f(2a -x))则函数f(x)在(0,2a)的图象关于直线x=a 偏移(偏对称)(俗称峰⾕偏函数)其中①极⼤值左偏(或右偏)也称峰偏左(或右)②极⼩值偏左(或偏右)也称⾕偏左(或右);性质:1) )(x f 的图象关于直线a x =对称若x 1,x 2∈(0,2a)x 1≠x 2则 x 1+x 2=2a <=>f (x 1)=f(x 2),(f ′(x 1)+f ′(x 2)=0,f ′(x 1+x 22)=0);2)已知函数是满⾜条件的极⼤值左偏(峰偏左)若x 1,x 2∈(0,2a)x 1≠x 2则f (x 1)=f(x 2)则x 1+x 2>2a ,及f ′(x 1+x 22)<0极值点偏移解题步骤:①求函数f(x)的极值点x 0;②构造函数F(x)=f(x+x 0)-f(x 0?x) (F(x)=f(x 0?x )-f(x 0+x), F(x)=f(x+2x 0)-f(?x) , F(x)=f(x)-f(2x 0?x))确定F(x)单调性③结合F(0)=0(F(-x 0)=0,F(x 0)=0)判断F(x)符号从⽽确定f(x+x 0),f(x 0?x)( f(x+2x 0)与f(?x); f(x)与f(2x 0?x))的⼤⼩关系; 答题模式:已知函数y=f(x)满⾜f (x 1)=f(x 2),x 0为函数y=f(x)的极值点,求证:x 1+x 2<2x 0 ①求函数f(x)的极值点x 0;②构造函数F(x)=f(x+x 0)-f(x 0?x) 确定F(x)单调性③判断F(x)符号从⽽确定f(x+x 0),f(x 0?x) 的⼤⼩关系;假设F(x)在(0,+∞)上单调递增则F(x)>F(0)=0,从⽽得到x>0时f(x+x 0)>f(x 0?x) ④1.(2016年全国I ⾼考)已知函数有两个零点. 设x 1,x 2是的两个零点,证明:+x 2<2.2. (2010年⾼考天津卷理科21)(本⼩题满分14分)已知函数f(x)=xe -x(x ∈R ).(Ⅰ) 求函数f(x)的单调区间和极值;(Ⅱ)已知函数y=g(x)的图象与函数y=f(x)的图象关于直线x=1对称,证明当x>1时,f(x)>g(x)(Ⅲ)如果12,x x ≠且12()(),f x f x =证明122x x +> 证明:由题意可知g(x)=f(2-x),得g(x)=(2-x)2x e-令F(x)=f(x)-g(x),即2()(2)xx F x xe x e --=+-于是22'()(1)(1)x x F x x ee --=--当x>1时,2x-2>0,从⽽2x-2e 10,0,F x e -->>⼜所以’(x)>0,从⽽函数F (x )在[1,+∞)是增函数。
导数压轴题分类(2)---极值点偏移问题(含答案)极值点偏移问题是在求解函数的极值点时,由于函数表达式的特殊性质,导致极值点位置发生偏移,需要采用特殊的解决方法。
常见的处理方法有以下几种:1.构造一元差函数F(x)=f(x)-f(2x-x)或F(x)=f(x+x)-f(x-x),其中x为函数y=f(x)的极值点。
2.利用对数平均不等式ab<a-b+a+b。
3.变换主元等方法lna-lnb^2<ln(a-b^2)。
接下来,我们以一个具体的例子来说明极值点偏移问题的解决方法。
题目:设函数f(x)=-alnx+x-ax(a∈R),试讨论函数f(x)的单调性;若f(x)=m有两解x1,x2(x12a。
解析:1.讨论函数f(x)的单调性由f(x)=-alnx+x-ax可知:f'(x)=-a/x+1-a=-(a/x+a-1)因为函数f(x)的定义域为(0,+∞),所以:①若a>0时,当x∈(0,a)时,f'(x)0,函数f(x)单调递增。
②若a=0时,当f'(x)=1/x>0在x∈(0,+∞)XXX成立,函数f(x)单调递增。
③若a0,函数f(x)单调递增。
2.求证x1+x2>2a因为f(x)=m有两解x1,x2(x1<x2),所以:alnx1+x1-ax=m,-alnx2+x2-ax=m将两式相减,整理得:lnx1-lnx2+ln(x1-x2)=a根据对数平均不等式,有:ln(x1-x2)<(lnx1-lnx2)/2代入上式得:a>-[(lnx1-lnx2)/2]化XXX:x1-x2<2e^-2a因为x1+x2>2x2>a,所以:x1+x2>2a综上所述,极值点偏移问题的解决方法包括构造一元差函数、利用对数平均不等式和变换主元等方法。
在具体求解中,需要根据函数表达式的特殊性质,选择合适的方法进行处理。
2(t-1)x2-1)/(4(t-1)2+1)为减函数,且在(1,∞)上递增,所以原不等式得证。
极值点偏移问题专题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(极值点偏移问题专题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为极值点偏移问题专题的全部内容。
极值点偏移问题专题(0)-—偏移新花样(拐点偏移)例1已知函数()22ln f x x x x =++,若正实数1x ,2x 满足()()12+=4f x f x , 求证:122x x +≥。
证明:注意到()1=2f ,()()()12+=21f x f x f ()()()12+=21f x f x f()2=+210f x x x '+>()22=2f x x''-+,()1=0f '',则(1,2)是()f x 图像的拐点,若拐点(1,2)也是()f x 的对称中心,则有12=2x x +,证明122x x +≥则说明拐点发生了偏移,作图如下想到了“极值点偏移”,想到了“对称化构造”,类似地,不妨将此问题命名为“拐点偏移",仍可用“对称化构造”来处理. 不妨设1201x x <≤≤,要证()()1221212212x x x x f x f x +≥⇔≥-≥⇔≥- ()()()()11114242f x f x f x f x ⇔-≥-⇔≥+-()()()2F x f x f x =+-,(]0,1x ∈,则()()()()222212212F x f x f x x x x x '''=--⎛⎫⎛⎫=++-+-+ ⎪ ⎪-⎝⎭⎝⎭()()141102xx x⎛⎫=--≥⎪⎪-⎝⎭,得()F x在(]0,1上单增,有()()()1214F x F≤=+=,得证。
导数极值点偏移问题知识整合:已知函数f(x)的图象的顶点的横坐标就是极值点x0,若f(x)=c 的两根的中点刚好满足122x x +=x0,即极值点在两根的正中间,也就是说极值点没有偏移.此时函数f(x)在x =x0两侧,函数值变化快慢相同,如图(1).2.若122x x +≠x0,则极值点偏移,此时函数f(x)在x =x0两侧,函数值变化快慢不同,如图(2)(3).典例:已知()21ln 2f x x x mx x =--,m ∈R .若()f x 有两个极值点1x ,2x ,且12x x <,求证:212e x x >(e 为自然对数的底数).解法一:齐次构造通解偏移套路 证法1:欲证212e x x >,需证12ln ln 2x x +>.若()f x 有两个极值点1x ,2x ,即函数()f x '有两个零点.又()ln f x x mx'=-,所以,1x,2x 是方程()0f x '=的两个不同实根.于是,有1122ln 0ln 0x mx x mx -=⎧⎨-=⎩,解得1212ln ln x x m x x +=+.另一方面,由1122ln 0ln 0x mx x mx -=⎧⎨-=⎩,得()2121ln ln x x m x x -=-, 从而可得,21122112ln ln ln ln x x x x x x x x -+=-+.于是,()()222121111222111lnln ln ln ln 1x x x x x x x x x x x x x x ⎛⎫+ ⎪-+⎝⎭+==--.又120x x <<,设21x t x =,则1t >.因此,()121ln ln ln 1t tx x t ++=-,1t >.要证12ln ln 2x x +>,即证:()1ln 21t t t +>-,1t >.即:当1t >时,有()21ln 1t t t ->+.设函数()()21ln 1t h t t t -=-+,1t ≥,则()()()()()()222212111011t t t h t t t t t +---'=-=≥++,所以,()h t 为()1.+∞上的增函数.注意到,()10h =,因此,()()10h t h ≥=.,当1t >时,有()21ln 1t t t ->+.所以,有12ln ln 2x x +>成立,212e x x >.求解本题的关键点有两个.一个是消参,把极值点转化为导函数零点之后,需要利用两个变量把参数表示出来,这是解决问题的基础,若只用一个极值点表示参数,如得到11ln x x m =之后,代入第二个方程,则无法建立两个极值点的关系,本题中利用两个方程相加(减)之后再消参,巧妙地把两个极值点与参数之间的关系建立起来;二是消“变”,即减少变量的个数,只有把方程转化为一个“变量”的式子后,才能建立与之相应的函数,转化为函数问题求解.本题利用参数m 的值相等建立方程,进而利用对数运算的性质,将方程转化为关于12x x 的方程,通过建立函数模型求解该问题,这体现了对数学建模等核心素养的考查.(消参减元)解法二 变换函数能妙解 证法2:欲证212e x x >,需证12ln ln 2x x +>.若()f x 有两个极值点1x ,2x ,即函数()f x '有两个零点.又()ln f x x mx'=-,所以,1x ,2x 是方程()0f x '=的两个不同实根.显然0m >,否则,函数()f x '为单调函数,不符合题意.由()11121222ln 0ln ln ln 0x mx x x m x x x mx -=⎧⇒+=+⎨-=⎩,即只需证明()122m x x +>即可.即只需证明122x x m +>.设()()210,g x f x f x x m m ⎛⎫⎛⎫⎛⎫''=--∈ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()()()22102mx g x x mx -'=>-,故()g x 在10,m ⎛⎫↑ ⎪⎝⎭,即()10g x g m ⎛⎫<= ⎪⎝⎭,故()2f x f x m ⎛⎫''<- ⎪⎝⎭. 由于()11mx f x m x x -''=-=,故()f x '在10,m ⎛⎫↑ ⎪⎝⎭,1,m ⎛⎫+∞↓ ⎪⎝⎭. 设121x x m <<,令1x x =,则()()2112f x f x f x m ⎛⎫'''=<- ⎪⎝⎭, 又因为2x ,121,x m m ⎛⎫-∈+∞ ⎪⎝⎭,()f x '在1,m ⎛⎫+∞↓ ⎪⎝⎭,故有212x x m >-,即122x x m +>.原命题得证.解法三 构造函数现实力证法3:由1x ,2x 是方程()0f x '=的两个不同实根得ln x m x =,令()ln xg x x =,()()12g x g x =,由于()21ln xg x x -'=,因此,()g x 在()1,e ↑,()e,+∞↓.设121e x x <<<,需证明212e x x >,只需证明()212e 0,e x x >∈,只需证明()212e f x f x ⎛⎫> ⎪⎝⎭,即()222e f x f x ⎛⎫> ⎪⎝⎭,即()222e 0f x f x ⎛⎫-> ⎪⎝⎭.即()()()()2e 1,e h x f x f x x ⎛⎫=-∈ ⎪⎝⎭,()()()22221ln e 0e x x h x x --'=>,故()h x 在()1,e ↑,故()()e 0h x h <=,即()2e f x f x ⎛⎫< ⎪⎝⎭.令1x x =,则()()2211e f x f x f x ⎛⎫=< ⎪⎝⎭,因为2x ,()21e e,x ∈+∞,()f x 在()e,+∞↓,所以221e x x >,即212e x x >.对称变换主要用来解决与两个极值点之和、积相关的不等式的证明问题.其解题要点如下:(1)定函数(极值点为x0),即利用导函数符号的变化判断函数单调性,进而确定函数的极值点x0.(2)构造函数,即根据极值点构造对称函数F(x)=f(x)-f(2x0-x),若证x1x2>2x ,则令F(x)=f(x)-f 20x x ⎛⎫ ⎪⎝⎭(3)判断单调性,即利用导数讨论F(x)的单调性.(4)比较大小,即判断函数F(x)在某段区间上的正负,并得出f(x)与f(2x0-x)的大小关系. (5)转化,即利用函数f(x)的单调性,将f(x)与f(2x0-x)的大小关系转化为x 与2x0-x 之间的关系,进而得到所证或所求.[提醒] 若要证明f ′122x x +⎛⎫ ⎪⎝⎭的符号问题,还需进一步讨论122x x +与x0的大小,得出122x x +所在的单调区间,从而得出该处导数值的正负.解法四 巧引变量(一)证法4:设()11ln 0,1t x =∈,()22ln 1,t x =∈+∞,则由1122ln 0ln 0x mx x mx -=⎧⎨-=⎩得11221122e e e t t t t t t m t m t -⎧=⇒=⎨=⎩,设120k t t =-<,则1e e 1k k k t =-,2e 1k k t =-.欲证212e x x >,需证12ln ln 2x x +>.即只需证明122t t +>,即()()()()()1e 21e 2e 11e 2e 10e 1k k k k k k k k k +>⇔+<-⇔+--<-.设()()()()1e 2e 10k k g k k k =+--<,()e e 1k k g k k '=-+,()e 0k g k k ''=<,故()g k '在(),0-∞↓,故()()00g k g ''>=,故()g k 在(),0-∞↑,因此()()00g k g <=,命题得证.解法五 巧引变量(二)证法5:设()11ln 0,1t x =∈,()22ln 1,t x =∈+∞,则由1122ln 0ln 0x mx x mx -=⎧⎨-=⎩得11221122e e e t t t t t t m t m t -⎧=⇒=⎨=⎩,设()120,1t k t =∈,则1ln 1k k t k =-,2ln 1k t k =-.欲证212e x x >,需证12ln ln 2x x +>,即只需证明122t t +>,即()()()1ln 21212ln ln 0111k k k k k k k k k +-->⇔<⇔-<-++,设()()()()21ln 0,11k g k k k k -=-⇔+,()()()22101k g k k k -'=>+,故()g k 在()0,1↑,因此()()10g k g <=,命题得证.比(差)值换元的目的也是消参、减元,就是根据已知条件首先建立极值点之间的关系,然后利用两个极值点之比(差)作为变量,从而实现消参、减元的目的.设法用比值或差值(一般用t 表示)表示两个极值点,继而将所求解问题转化为关于t 的函数问题求解.变式1.已知函数()()x f x xe x R -=∈.(1)判断函数()f x 的单调性;(2)如果12x x ≠,且()()12f x f x =,求证:122x x +>.解:(1)因为()xf x xe -=,所以()()1xf x x e -'=-,.可得函数()xf x xe -=在(),1-∞上单调递增,在()1,+∞上单调递减.(2)证明:由()()12f x f x =,12x x ≠,不妨设12x x <,构造函数()()()11F x f x f x =+--,(]0,1x ∈,则()()()()211110xx x F x f x f x e e+'''=++-=->, 所以()F x 在(]0,1x ∈上单调递增,()()00F x F >=,也即()()11f x f x +>-对(]0,1x ∈恒成立.由1201x x <<<,则(]110,1x -∈,所以()()()()()()()1111211211f x f x f x f x f x +-=->--==,即()()122f x f x ->,又因为12x -,()21,x ∈+∞,且()f x 在()1,+∞上单调递减,所以122x x -<,即122x x +>.变式2.已知函数()2cos f x x xπ=+(1)求函数()f x 的最小值;(2)若函数()()g x f x a=-在()0,∞+上有两个零点1x ,2x ,且12xx <,求证:12232x x π+<.【答案】(1)()2min 4f x π=(2)证明见解析;(1)()2cos f x x x π=+,()()2cos f x x x f x π-=+=,()f x 为偶函数,故只需求[)0,x ∈+∞时()f x 的最小值,()2sin f x x x π'=-,当0,2x π⎛⎫∈ ⎪⎝⎭时,设()2sin h x x x π=-, ()2cos h x x π'=-,显然()h x '单增,而()00h '<,02h π⎛⎫'> ⎪⎝⎭, 由零点存在定理,存在唯一的00,2x π⎛⎫∈ ⎪⎝⎭,使得()00h x '=, 当()00,x x ∈,()0h x '<,()h x 单减,当0,2x x π⎛⎫∈ ⎪⎝⎭,()0h x '>,()h x 单增, 而()00h =,02h π⎛⎫= ⎪⎝⎭,故0,2x π⎛⎫∈ ⎪⎝⎭,()0h x <, 即0,2x π⎛⎫∈ ⎪⎝⎭,()0f x '<,()f x 单减; 又当,2x π⎡⎫∈+∞⎪⎢⎣⎭,2sin x x ππ>>,()0f x '>,()f x 单增,所以()n2mi 24f x f ππ⎛⎫==⎪⎝⎭.(2)11212212123131222223332x x x x x x x x x x ++++++=<=, 只需证1222x x π+<,由(1)得10,2x π⎛⎫∈ ⎪⎝⎭,2,2x π⎛⎫∈+∞ ⎪⎝⎭, 构造函数()()()F x f x f x π=--,0,2x π⎛⎫∈ ⎪⎝⎭,()()()22sin 0F x f x f x x πππ'''=+-=->,即()F x 单增,所以()02F x F π⎛⎫<= ⎪⎝⎭,即当0,2x π⎛⎫∈ ⎪⎝⎭时,()()f x f x π<-, 而10,2x π⎛⎫∈ ⎪⎝⎭,所以()()11f x f x π<-,又()()12f x f x =, 即()()21f x f x π<-,此时2x ,1,2x ππ⎛⎫-∈+∞ ⎪⎝⎭,()f x 在,2π⎛⎫+∞ ⎪⎝⎭单增,所以21x x π<-,12x x π+<,即证1222x x π+<.变式3.(2020•安徽模拟)已知f (x )=2x+1﹣eax (a ∈R ).若x1,x2为方程f (x )=1的两个相异的实根,求证:x1+x2.【解析】证明:x1,x2为方程f (x )=1的两个相异的实根,则x1,x2为方程2x ﹣eax =0的两个相异的实根,即x1,x2为方程ax =ln (2x )的两个相异的实根, ∴ax1=ln (2x1),ax2=ln (2x2).不妨设x1>x2>0.∴a (x1﹣x2)=ln ,即a .证明:x1+x2⇔a .因此只要证明:.即证明ln即可.令t>1.上述不等式等价于:g(t)=lnt0(t>1),g(1)=0.g′(t)0,∴函数g(t)在(1,+∞)上单调递增,∴g(t)>g(1)=0,∴ln成立.即x1+x2.变式4..(2020•抚顺模拟)已知函数f(x)=lnx﹣tx+t.当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:.【解析】证明:由f(x)=m﹣ax,得lnx+(a﹣2)x+2﹣m=0.令g(x)=lnx+(a﹣2)x+2,则g(x1)=g(x2)=m.即lnx1+(a﹣2)x1=lnx2+(a﹣2)x2,∴a﹣2.不妨设0<x1<x2,要证,只需证2(2﹣a),即证.令(c>1),g(c)=2lnc﹣c,∵g′(c)0.∴g(c)在(1,+∞)上单调递减,则g(c)<g(1)=0.故成立.变式5.设函数()()22lnf x x a x a x=---.(1)求函数()f x 的单调区间;(2)若方程()f x c =有两个不相等的实数根1x ,2x,求证:12()02x x f +'>.【答案】(1)(0,)x ∈+∞.22(2)(2)(1)()2(2)a x a x a x a x f x x a x x x ----+'=---==.当0a 时,()0f x '>,函数()f x 在(0,)+∞上单调递增,即()f x 的单调递增区间为(0,)+∞.当0a >时,由()0f x '>得2a x >;由()0f x '<,解得02ax <<.所以函数()f x 的单调递增区间为(,)2a +∞,单调递减区间为(0,)2a . (2)1x ,2x 是方程()f x c =得两个不等实数根,由(1)可知:0a >. 不妨设120x x <<.则()21112ln x a x a x c---=,()22222ln x a x a x c---=.两式相减得()()221112222ln 2ln 0x a x a x x a x a x ----+-+=,化为221122112222ln ln x x x x a x x x x +--=+--.()02a f '=,当(0,)2a x ∈时,()0f x '<,当(,)2a x ∈+∞时,()0f x '>. 故只要证明1222+>x x a即可, 即证明22112212112222ln ln x x x x x x x x x x +--+>+--,即证明11221222ln x x x x x x -<+, 设12(01)x t t x =<<,令()22ln 1t g t t t -=-+,则22214(1)()(1)(1)t g t t t t t -'=-=++. 10t >>,()0g t ∴'>.()g t ∴在(0,1)上是增函数,又在1t =处连续且g (1)0=,∴当(0,1)t ∈时,()0g t <总成立.故命题得证.。
专题09极值点偏移(二)一.考情分析函数的极值点偏移问题,是导数应用问题,呈现的形式往往非常简洁,涉及函数的双零点,是一个多元数学问题,不管待证的是两个变量的不等式,还是导函数的值的不等式,解题的策略都是把双变量的等式或不等式转化为一元变量问题求解,途径都是构造一元函数.二.经验分享1、极值点偏移的判定定理对于可导函数)(x f y =,在区间),(b a 上只有一个极大(小)值点0x ,方程0)(=x f 的解分别为21,x x ,且b x x a <<<21,(1)若)2()(201x x f x f -<,则021)(2x x x ><+,即函数)(x f y =在区间),(21x x 上极(小)大值点0x 右(左)偏;(2)若)2()(201x x f x f ->,则021)(2x x x <>+,即函数)(x f y =在区间),(21x x 上极(小)大值点0x 右(左)偏.2、运用判定定理判定极值点偏移的方法 1、极值点偏移处理方法:(1)求出函数)(x f 的极值点0x ;(2)构造一元差函数)()()(00x x f x x f x F --+=; (3)确定函数)(x F 的单调性;(4)结合0)0(=F ,判断)(x F 的符号,从而确定)(0x x f +、)(0x x f -的大小关系. 口诀:极值偏离对称轴,构造函数觅行踪;四个步骤环相扣,两次单调紧跟随. 2、答题模板若已知函数)(x f 满足)()(21x f x f =,0x 为函数)(x f 的极值点,求证:0212x x x <+. (1)讨论函数)(x f 的单调性并求出)(x f 的极值点0x ;假设此处)(x f 在),(0x -∞上单调递减,在),(0+∞x 上单调递增. (2)构造)()()(00x x f x x f x F --+=;注:此处根据题意需要还可以构造成)2()()(0x x f x f x F --=的形式. (3)通过求导)('x F 讨论)(x F 的单调性,判断出)(x F 在某段区间上的正负,并得出)(0x x f +与)(0x x f -的大小关系;假设此处)(x F 在),0(+∞上单调递增,那么我们便可得出0)()()()(000=-=>x f x f x F x F ,从而得到:0x x >时,)()(00x x f x x f ->+.(4)不妨设201x x x <<,通过)(x f 的单调性,)()(21x f x f =,)(0x x f +与)(0x x f -的大小关系得出结论;接上述情况,由于0x x >时,)()(00x x f x x f ->+且201x x x <<,)()(21x f x f =,故)2()]([)]([)()(2002002021x x f x x x f x x x f x f x f -=-->-+==,又因为01x x <,0202x x x <-且)(x f 在),(0x -∞上单调递减,从而得到2012x x x -<,从而0212x x x <+得证.(5)若要证明0)2('21<+x x f ,还需进一步讨论221x x +与0x 的大小,得出221x x +所在的单调区间,从而得出该处函数导数值的正负,从而结论得证.此处只需继续证明:因为0212x x x <+,故0212x x x <+,由于)(x f 在),(0x -∞上单调递减,故0)2('21<+x x f . 【说明】(1)此类试题由于思路固定,所以通常情况下求导比较复杂,计算时须细心;(2)此类题目若试题难度较低,会分解为三问,前两问分别求)(x f 的单调性、极值点,证明)(0x x f +与)(0x x f -(或)(x f 与)2(0x x f -)的大小关系;若试题难度较大,则直接给出形如0212x x x <+或0)2('21<+x x f 的结论,让你给予证明,此时自己应主动把该小问分解为三问逐步解题.三、题型分析例1.已知函数()()2ln f x x x ax x a a R =+-+∈在其定义域内有两个不同的极值点.(1)求a 的取值范围.(2)设()f x 的两个极值点为12,x x ,证明212x x e >.【解析】:(1)依题意,函数()f x 的定义域为()0,+∞,所以方程()0f x '=在()0,+∞有两个不同根.即方程ln 20x ax +=在()0,+∞有两个不同根. 转化为,函数()ln xg x x=与函数2y a =-的图象在()0,+∞上有两个不同交点 又()21ln xg x x-'=,即0x e <<时, ()0g x '>, x e >时,()0g x '<, 所以()g x 在()0,e 上单调增,在(),e +∞上单调减,从而()()1=g x g e e=极大.又()g x 有且只有一个零点是1,且在0x →时,()g x →-∞,在x →+∞时, ()0g x →,所以由()g x 的图象,要想函数()ln xg x x =与函数2y a =-的图象在()0,+∞上有两个不同交点, 只需102a e <-<,即102a e<<-(2)由(1)可知12,x x 分别是方程ln 0x ax -=的两个根,即11ln x ax =, 22ln x ax =,设120x x >>,作差得, ()1122ln x a x x x =-,即1212lnx x a x x =-.原不等式212x x e >等价于12ln ln 2x x +> ()122a x x ⇔+> ()1212122ln x x x x x x -⇔>+ 令12x t x =,则1t >,()()121212221ln ln 1x x t x t x x x t -->⇔>++, 设()()21ln 1t g t t t -=-+, 1t >,()()()22101t g t t t +'-=>,∴函数()g t 在()1,+∞上单调递增, ∴()()10g t g >=,即不等式()21ln 1t t t ->+成立,故所证不等式212x x e >成立.【方法总结】:利用导数证明不等式常见类型及解题策略:(1) 构造差函数()()()h x f x g x =-.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式.(2) 根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数. 例2.已知函数()()()2a xg x xea R -=∈, e 为自然对数的底数.(1)讨论()g x 的单调性;(2)若函数()()2ln f x g x ax =-的图象与直线()y m m R =∈交于A B 、两点,线段AB 中点的横坐标为0x ,证明: ()00f x '<(()f x '为函数()f x 的导函数) 【答案】(1)略(2)见解析 【解析】∵()()()()222ln ln 2(0)a xf x xe axx a x ax x -=-=+-->,∴()()()()211122x ax f x a ax x x+-=+--'=-, 当0a ≤时, ()()0,f x y g x >'=在()0,+∞上单调递增,与直线y m =不可能有两个交点,故0a >.令()0f x '≥,则10x a <≤;令()0f x '<,则1x a >,故()y g x =在10,a ⎛⎤⎥⎝⎦上单调递增,在1,a ⎛⎫+∞⎪⎝⎭上单调递减.不妨设()()12,,,A x m B x m ,且1210x x a <<<,要证()00f x '<,需证010ax ->, 即证()01221211222x x x x x f x f x a a a a ⎛⎫>⇒+>⇒>-⇒<- ⎪⎝⎭, 又()()12f x f x =,所以只需证()112f x f x a ⎛⎫<-⎪⎝⎭,即证:当10x a <<时,()20f x f x a ⎛⎫--> ⎪⎝⎭. 设()()()()2ln 2ln 22F x f x f x ax ax ax a ⎛⎫=--=--+-⎪⎝⎭, 则()()()22112022ax a F x a ax x x ax --=-+=-<--',∴()()2F x f x f x a ⎛⎫=--⎪⎝⎭在10,a ⎛⎫ ⎪⎝⎭上单调递减,又12110F f f a a a a ⎛⎫⎛⎫⎛⎫=--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 故()()20F x f x f x a ⎛⎫=-->⎪⎝⎭,原不等式成立. 例3.已知()21ln 2f x x x mx x =--,m ∈R .若()f x 有两个极值点1x ,2x ,且12x x <,求证:212e x x >(e 为自然对数的底数).【解析】(方法一)构造函数现实力【证明】:由1x ,2x 是方程()0f x '=的两个不同实根得ln x m x =,令()ln xg x x=,()()12g x g x =,由于()21ln xg x x-'=,因此,()g x 在()1,e ↑,()e,+∞↓. 设121e x x <<<,需证明212e x x >,只需证明()212e 0,e x x >∈,只需证明()212e f x f x ⎛⎫> ⎪⎝⎭,即()222e f x f x ⎛⎫> ⎪⎝⎭,即()222e 0f x f x ⎛⎫-> ⎪⎝⎭. 即()()()()2e 1,e h x f x f x x ⎛⎫=-∈ ⎪⎝⎭,()()()22221ln e 0e x x h x x --'=>,故()h x 在()1,e ↑,故()()e 0h x h <=,即()2e f x f x ⎛⎫< ⎪⎝⎭.令1x x =,则()()2211e f x f x f x ⎛⎫=< ⎪⎝⎭,因为2x ,()21e e,x ∈+∞,()f x 在()e,+∞↓,所以221e x x >,即212e x x >. (方法二)巧引变量【证明】:设()11ln 0,1t x =∈,()22ln 1,t x =∈+∞,则由1122ln 0ln 0x mx x mx -=⎧⎨-=⎩得11221122e e et t t t t t m t m t -⎧=⇒=⎨=⎩,设120k t t =-<,则1e e 1k k k t =-,2e 1kk t =-.欲证212e x x >,(方法三)巧引变量【证明】:设()11ln 0,1t x =∈,()22ln 1,t x =∈+∞,则由1122ln 0ln 0x mx x mx -=⎧⎨-=⎩得11221122e e e t t t t t t m t m t -⎧=⇒=⎨=⎩,设()120,1t k t =∈,则1ln 1k k t k =-,2ln 1k t k =-. 欲证212e x x >,需证12ln ln 2x x +>,即只需证明122t t +>,即()()()1ln 21212ln ln 0111k k k k k k k k k +-->⇔<⇔-<-++,设()()()()21ln 0,11k g k k k k -=-⇔+,()()()22101k g k k k -'=>+, 故()g k 在()0,1↑,因此()()10g k g <=,命题得证. 例4.已知函数()ln f x x a x =+与()3bg x x=-的图象在点()1,1处有相同的切线. (Ⅰ)若函数()2y x n =+与()y f x =的图象有两个交点,求实数n 的取值范围; (Ⅰ)若函数()()()3222m mF x x g x f x ⎛⎫=-+- ⎪⎝⎭有两个极值点1x ,2x ,且12x x <,证明:()221F x x <-.【答案】(Ⅰ)1,2⎛⎫-∞-⎪⎝⎭;(Ⅰ)证明过程见解析; (Ⅰ)由题意,函数()2ln mF x x x x=--,其定义域为()0,+∞, ()22222'1m x x mF x x x x-+=+-=, 令()'0F x =,得220x x m -+=,其判别式44m ∆=-,函数()F x 有两个极值点1x , 2x ,等价于方程220x x m -+=在()0,+∞内有两不等实根,又120x x >,故01m <<.所以211x m =+-,且212x <<, 2222m x x =-+,()22222222222212ln 12ln 1x x F x x x x x x x x -+-+=---+=--,令()2ln 1h t t t =--, 12t <<, 则()22'1t h t t t-=-=, 由于12t <<,∴()'0h t <,故()h t 在()1,2上单调递减. 故()()112ln110h t h <=--=. 所以()()22210F x x h x -+=<, 所以()221F x x <-.【方法总结】:此题主要考查函数导数的几何意义,以及函数单调性、最值在不等式证明中的综合应用能力等有关方面的知识,属于高档题型,也是高频考点.在问题(Ⅰ)中根据导数几何意义建立方程组,求出函数()f x 解析式,再由题意构造函数()T x ,将问题转化为求函数()T x 的零点个数,利用导数求出函数()T x 的最值、单调区间,从而求出实数n 的取值范围;在问题(Ⅰ)中,由(Ⅰ)可求出函数()F x 的解析式,依据导数与极值点的关系求出参数m 的范围,并求出参数m 与极值点2x 的关系式,根据问题构造新的函数()h t ,再用函数()h t 的单调性证明不等式成立.例5.已知函数()()21ln 1f x x a x =-+-, a R ∈.(Ⅰ)若函数()f x 为定义域上的单调函数,求实数a 的取值范围; (Ⅰ)若函数()f x 存在两个极值点1x , 2x ,且12x x <,证明:()()1221f x f x x x >.【答案】(1)1,2⎛⎫+∞⎪⎝⎭.(2)详见解析. 【解析】因为函数()f x 有两个极值点,所以()'0f x =在1x <上有两个不等的实根, 即2220x x a -+-=在1x <有两个不等的实根1x , 2x ,于是102a <<, 12121,{,2x x a x x +==且满足110,2x ⎛⎫∈ ⎪⎝⎭, 21,12x ⎛⎫∈ ⎪⎝⎭,()()()()()()()2111111211112221ln 1112ln 112ln 1f x x a x x x x x x x x x x x x -+--++-===-++-,同理可得()()()2222112ln 1f x x x x x =-++-.()()()()()()1221112222222212ln 12ln 12121ln 2ln 1f x f x x x x x x x x x x x x x x -=-+---=-+---,令()()()2121ln 2ln 1g x x x x x x =-+---, 1,12x ⎛⎫∈⎪⎝⎭. ()()22'2ln 11x g x x x x x ⎡⎤=--++⎣⎦-, 1,12x ⎛⎫∈ ⎪⎝⎭, ∵()114x x -<,∴()2ln 10x x ⎡⎤-->⎣⎦, 又1,12x ⎛⎫∈⎪⎝⎭时, 2201x x x +>-,∴()'0g x >,则()g x 在1,12x ⎛⎫∈ ⎪⎝⎭上单调递增,所以()102g x g ⎛⎫>= ⎪⎝⎭,即()()12210f x f x x x ->,得证.例6.已知函数()()2ln 2,g x x ax a x a R =-+-∈.(1)求()g x 的单调区间;(2)若函数()()()212f x g x a x x =++-, 1212,()x x x x <是函数()f x 的两个零点,()f x '是函数()f x 的导函数,证明: 1202x x f +⎛⎫<⎪⎝⎭'. 【答案】(1)见解析(2)见解析【解析】(1)先求函数导数,根据导函数是否变号进行讨论,当0a ≤时, ()0g x '>, ()g x 递增,当0a >时,导函数有一零点,导函数先正后负,故得增区间为10,a ⎛⎫⎪⎝⎭,减区间为1,a ⎛⎫+∞ ⎪⎝⎭;(2)利用分析法先等价转化所证不等式:要证明1202x x f +⎛⎫<⎪⎝⎭',只需证明121212ln ln 20x x x x x x --<+- 12(0)x x <<,即证明()1212122ln ln x x x x x x ->-+,即证明12112221ln 1x x x x x x ⎛⎫- ⎪⎝⎭>+,再令()120,1x t x =∈,构造函数()()1ln 22h t t t t =+-+,利用导数研究函数()h t 单调性,确定其最值: ()h t 在()0,1上递增,所以()()10h t h <=,即可证得结论.试题解析:(1) ()g x 的定义域为()0,+∞, ()()122g x ax a x-'=+- 当0a ≤时, ()0g x '>, ()g x 递增当0a >时, ()()()()()2221211122ax a x x ax g x ax a x x x -+-++-'+=-+-==()()10,0,xg x g x a '<递增; ()()1,0,x g x g x a'><递减 综上:∴当0a >时, ()g x 的单调增区间为10,a ⎛⎫ ⎪⎝⎭,单调减区间为1,a ⎛⎫+∞ ⎪⎝⎭当0a ≤时, ()g x 的单调增区间为()0,+∞即证明()1212122ln ln x x x x x x ->-+,即证明()12112221ln *1x x x x x x ⎛⎫- ⎪⎝⎭>+令()120,1x t x =∈,则()()1ln 22h t t t t =+-+ 则()1ln 1h t t t +'=-, ()2110h t t t-'=<' ∴()h t '在()0,1上递减, ()()10h t h ''>=,∴()h t 在()0,1上递增, ()()10h t h <= 所以()*成立,即1202x x f +⎛⎫<⎪⎝⎭' 【方法总结】:利用导数证明不等式常见类型及解题策略(1) 构造差函数()()()h x f x g x =-.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.四、迁移应用1.已知函数()e xf x ax =-有两个不同的零点1x ,2x ,其极值点为0x .(1)求a 的取值范围;(2)求证:1202x x x +<; (3)求证:121x x <.【解析】:(1)()e xf x a '=-,若0a ≤,则()0f x '>,()f x 在R 上单调递增,()f x 至多有一个零点,舍去;则必有0a >,得()f x 在(),ln a -∞上递减,在()ln ,a +∞上递增,要使()f x 有两个不同的零点,则须有()ln 0e f a a <⇒>. (严格来讲,还需补充两处变化趋势的说明:当x →-∞时,()f x →+∞;当x →+∞时,()f x →+∞).(3)构造函数()()1G x g x g x ⎛⎫=-⎪⎝⎭,则 ()()()()()1122222111e 1e 111e e 1x xx x G x g x g x x x x x x x x x x ⎛⎫'''=+⎪⎝⎭⎛⎫- ⎪-⎝⎭=+⋅⎛⎫⎪⎝⎭-=-⋅当01x <<时,10x -<,但因式1e e x xx -的符号不容易看出,引进辅助函数()1e e xx x x ϕ=-,则()11e 1e xxx xϕ⎛⎫'=+- ⎪⎝⎭,当()0,1x ∈时,()0x ϕ'>,得()x ϕ在()0,1上递增,有()()10x ϕϕ<=,则()0G x '>,得()G x 在()0,1上递增,有()()10G x G <=,即()()101g x g x x ⎛⎫<<<⎪⎝⎭; (iii )将1x 代入(ii )中不等式得()()1211g x g x g x ⎛⎫=<⎪⎝⎭,又21x >,111x >,()g x 在()1,+∞上递增,故211x x <,121x x <. 【方法总结】:虽然做出来了,但判定因式()222e e 2x x x x ---及1e e xx x -的正负时,均需要辅助函数的介入,费了一番功夫,虽然()g x 的极值点是1,理论上可以用来做(3)、(4)两问,但实践发现略显麻烦,我们还没有找到理想的函数. 再次回到题设条件:()()0e e ln ln ln ln x f x ax a x a x x x a =⇔=>⇔=+⇔-=,记函数()ln h x x x =-,则有()()12ln h x h x a ==.接下来我们选取函数()h x 再解(3)、(4)两问. (3)(i )()11h x x'=-,得()h x 在()0,1上递减,在()1,+∞上递增,有极小值()11h =,又当0x +→时,()h x →+∞;当x →+∞时,()h x →+∞, 由()()12h x h x =不妨设1201x x <<<. 2已知函数()211xx f x e x-=+. (1)求()f x 的单调区间;(2)证明:当()()()1212f x f x x x =≠时,120x x +<.【解析】 (1) ()f x 在(),0-∞上单调递增,在()0,+∞上单调递减; (2)由(1)知当1x <时,()0f x >. 不妨设12x x <,因为()()12f x f x =,即121222121111x x x x e e x x --=++,则1201x x <<<, 要证明120x x +<,即120x x <-<,只需证明()()12f x f x <-,即()()22f x f x <-.而22()()f x f x <-等价于2222(1)10xx e x ---<,令()2()(1)10xg x x ex x =--->,则2'()(12)1x g x x e =--,令2()(12)1xh x x e=--,则2()40x h x xe '=-<,所以()h x 单调递减,()()00h x h <=,即()0g x '<,所以()g x 单调递减,所以()()00g x g <=,得证.3.已知函数2)1()2()(-+-=x a e x x f x有两个零点21,x x .证明:122x x +<. 【解析】 参变分离再构造差量函数由已知得:()()120f x f x ==,不难发现11x ≠,21x ≠,故可整理得:()()()()121222122211x x x e x e a x x ---==--设()()()221x x e g x x -=-,则()()12g x g x = 那么()()()2321'1x x g x e x -+=-,当1x <时,()'0g x <,()g x 单调递减;当1x >时,()'0g x >,()g x 单调递增. 设0m >,构造代数式:()()111222*********m m m m m m m m g m g m e e e e m m m m +-----+-⎛⎫+--=-=+ ⎪+⎝⎭设()2111mm h m e m -=++,0m > 则()()2222'01m m h m e m =>+,故()h m 单调递增,有()()00h m h >=.因此,对于任意的0m >,()()11g m g m +>-.由()()12g x g x =可知1x 、2x 不可能在()g x 的同一个单调区间上, 不妨设12x x <,则必有121x x <<令110m x =->,则有()()()()()1111211112g x g x g x g x g x +->--⇔->=⎡⎤⎡⎤⎣⎦⎣⎦ 而121x ->,21x >,()g x 在()1,+∞上单调递增,因此:()()121222g x g x x x ->⇔-> 整理得:122x x +<.【其他解法】:利用“对数平均”不等式参变分离得:222211)1()2()1()2(21--=--=x e x x e x a x x ,由0>a 得,2121<<<x x ,将上述等式两边取以e 为底的对数,得22221211)1()2(ln )1()2(lnx x x x x x +--=+--, 化简得:21212221)]2ln()2[ln(])1ln()1[ln(x x x x x x -=-------,故2121212221)]2ln()2[ln(])1ln()1[ln(1x x x x x x x x ---------= )2()2()]2ln()2[ln()1()1(])1ln()1[ln()]1()1[(21212221222121x x x x x x x x x x ------+-------+-= 由对数平均不等式得:221222221212[ln(-1)-ln(-1)]2(1)(1)(1)(1)x x x x x x >----+-, 121212[ln(2-)-ln(2-)]22222x x x x x x >----+-()()()(),从而122212122(2)21(1)(1)22x x x x x x +->+-+--+-()()1212122212122(2)[4()]2(1)(1)4()x x x x x x x x x x +--+++-=+-+--+12122212122(2)21(1)(1)4()x x x x x x x x +-+-=++-+--+等价于:12122212122(2)20(1)(1)4()x x x x x x x x +-+->+-+--+ 1222121221(2)[](1)(1)4()x x x x x x =+-+-+--+由221212(1)(1)0,4()0x x x x -+->-+>,故122x x +<,证毕.4已知函数()ln xf x x a=+(a R ∈),曲线()y f x =在点()()1,1f 处的切线与直线10x y ++=垂直.(1)试比较20172016与20162017的大小,并说明理由;(2)若函数()()g x f x k =-有两个不同的零点12,x x ,证明: 212•x x e >.【答案】(1)2017201620162017>(2)见解析【解析】:(1)依题意得()()2ln x ax x f x x a +-+'=, 所以()()21111af x aa +==++',又由切线方程可得()11f '=,即111a =+,解得0a =此时()ln x f x x =, ()21ln xf x x -'=, 令()0f x '>,即1ln 0x ->,解得0x e <<; 令()0f x '<,即1ln 0x -<,解得x e > 所以()f x 的增区间为()0,e ,减区间为(),e +∞ 所以()()20162017f f >,即ln2016ln201720162017>, 2017ln20162016ln2017>, 2017201620162017>.(2)证明:不妨设120x x >>因为()()120g x g x == 所以化简得11ln 0x kx -=, 22ln 0x kx -=可得()1212ln ln x x k x x +=+, ()1212ln ln x x k x x -=-.要证明212x x e >,即证明12ln ln 2x x +>,也就是()122k x x +>因为1212ln ln x x k x x -=-,所以即证121212ln ln 2x x x x x x ->-+即112212lnx x x x x x ->+,令12x t x =,则1t >,即证()21ln 1t t t ->+. 令()()21ln 1t h t t t -=-+(1t >),由()()()()222114011t h t t t t t -=-=+'>+故函数()h t 在()1,+∞是增函数,所以()()10h t h >=,即()21ln 1t t t ->+得证.所以212x x e >.【方法总结】:本题主要考查函数导数与切线的关系,考查利用导数来证明不等式,考查利用分析法和导数来证明不等式的方法.有关导数与切线的问题,关键的突破口在与切点和斜率,本题中已知切线和某条直线垂直,也即是给出斜率,利用斜率可求得函数的参数值.利用导数证明不等式通常先利用分析法分析,通过转化后再利用导数来证明. 5.已知函数(1)(1ln )(),()ln ()x x f x g x x mx m R x++==-∈(1)求函数()g x 的单调区间;(2)当0m >时,对任意的[]11,2x ∈,存在[]21,2x ∈,使得12()3()f x m g x ->成立,试确定实数m 的取值范围。