向量的加减法运算
- 格式：docx
- 大小：62.91 KB
- 文档页数：2
下载文档原格式
合集下载
向量的加减法运算法则
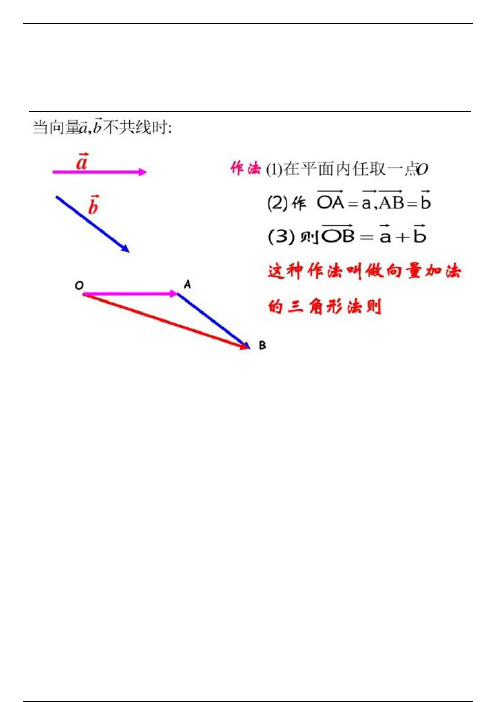
向量的加减法运算法则
在向量的加减法运算中，可以用向量的模量和方向来进行计算，并且有四种基本计算规则，分别是：
1、向量的加法：将两个向量在平面上以具有相同方向性的标准坐标系下把向量放在一起，然后把它们合并在一起，将每一个坐标轴上的分量所对应的向量分量累加在一起即可得到两个向量之和。
2、向量的减法：将两个向量以相反方向放在一起，然后把它们合并在一起，将每一个坐标轴上的分量所对应的向量分量累减在一起即可得到两个向量之差。
3、向量的乘法：将两个向量的模量乘在一起，然后乘以向量夹角的余弦值，即可得到两个向量之积。
4、向量的除法：将一个向量的模量除以另一个向量的模量，然后乘以向量夹角的余弦值，即可得到两个向量的商。
向量的加减法是数学中一个基本的操作，但是要掌握它就必须正确理解向量的含义，以及向量的模量和方向性。
如果运算错误，得到的结果可能是不正确的，因此一定要仔细检查计算的准确性，以保证求得的结果是正确的。
2.2.向量加减法、数乘运算及其几何意义
向量加减法向量的加减法平面向量加减法加减法运算加减法互为逆运算加减法简便运算小数加减法简便运算向量运算空间向量与立体几何向量的运算
2.2.向量加法、减法运算 及其几何意义
1、位移
AB + BC = AC
C A B F1
2、力的合成
F1 + F2 = F
F2
F
数的加法启发我们，从运算的角度看， AC可以认为 是AB与BC的和，F可以认为是F1与F2的和，即位移、力的 合成可以看作向量的加法。
(1)同向
a
(2)反向
a
b
A
B C B C
b
A
AC = a + b
规定： a + 0 = 0 + a = a
AC = a + b
当向量a ,b不是共线向量时,a + b又如何 作出来?
b a
o·
a
A
a+ b
b
B
| a+ b|< | a|+ |b| 一般地，有 | a + b |? | a | |b|
E
3AB BC
3 AC
∴ AC与 AE 共线．
作业：
课本P 4, P 5, P 4 84 90 91
数的加法满足交换律与结合律，即对任意a，b∈R，有
a+b=b+a
任意向量
a、 b
(a+b)+c=a+(b+a)
的加法是否也满足交换律与结合律？
a+ b = b+ a (a + b) + c = a + (b + c )
2.2.向量加法、减法运算 及其几何意义
1、位移
AB + BC = AC
C A B F1
2、力的合成
F1 + F2 = F
F2
F
数的加法启发我们，从运算的角度看， AC可以认为 是AB与BC的和，F可以认为是F1与F2的和，即位移、力的 合成可以看作向量的加法。
(1)同向
a
(2)反向
a
b
A
B C B C
b
A
AC = a + b
规定： a + 0 = 0 + a = a
AC = a + b
当向量a ,b不是共线向量时,a + b又如何 作出来?
b a
o·
a
A
a+ b
b
B
| a+ b|< | a|+ |b| 一般地，有 | a + b |? | a | |b|
E
3AB BC
3 AC
∴ AC与 AE 共线．
作业：
课本P 4, P 5, P 4 84 90 91
数的加法满足交换律与结合律，即对任意a，b∈R，有
a+b=b+a
任意向量
a、 b
(a+b)+c=a+(b+a)
的加法是否也满足交换律与结合律？
a+ b = b+ a (a + b) + c = a + (b + c )
向量的加减法
的终点的向量.
向量的减法：
a
O
a a b
A
b b
B
起 点 相 同
指向被减向量
已知向量 a 、 b , 在平面内任取一点O，作OA a, OB b, 则向量 BA叫做 a与b 的差，记作 a b, 即 a b OA OB BA 这种求向量差的方法，叫做向量减法的三角形法则。
a
对 于 零 向 量 与 任 一 向a 量 ,我们规定 a 0 0 a a
对于向量的加法的理解需要注意下面两点: (1)两个向量的和仍然是向量(简称和向量) (2)位移的合成是三角形法则的物理模型.
例1.如图，已知向量 a, b ，求做向量
作法1：在平面内任取一点O， 作 OA a ，AB b ， 则 OB a b 。
总结向量加法的“三角形法则”与 “平行四边形”法则的联系与区别。
向量加法的平行四边形法则和三角形法则 的区别与联系
• 三角形法则中的两个向量是首尾相接的，而 平行四边形法则中的两个向量有公共的起点；三 角形法则适用于所有的两个非零向量的求和，而 平行四边形法则仅适用于不共线的两个向量的求 和。三角形法则和平行四边法则虽然都是求向量 和的基本方法。但在应用上也有讲究，求两个向 量和，当一个向量的终点为另一个向量的始点时， 可用向量加法的三角形法则；而当它们的始点相 同时，可用向量加法的平行四边形法则。
b
a b
(2)连接两向量的终点,方向指向被减向量
注意与作和向量的区别
练习2：
DB 1、 AB AD __________
CA 2、 BA BC __________
AC 3、 BC BA __________
高一数学向量的加减法
B
A
. O
. N
2, 填空
AB - AD = DB BA - BC = CA
BC - BA =
OD - OA =
AC
AD
BA
OA - OB =
(3)填空
(1) (2) (3) AB - AC - CB = 0
AB + BC - AD
AB + BC - DC AB - AC + BC
=
= =
DC
AD
先复习向量的加法
b
a
a 三角形法则
-----首尾相接首到尾
平行四边形法则
----相同起点对角线
同学们学习了向量的加法，接 下来我们要学习
向量的减法
c
b
如图:
a+b= c
c-a = b
移项得:
a
c a b
这么说来，向量c与向量a进 行了减法运算，得到向量b。 像这样求两个向量的差的运 算叫做向量的减法。 那么向量的减法有什么 规律呢？
(4)
0
课堂小结:
(1)向量减法的概念.
(2)向量减法可以看作一个向量 加上另一个向量的相反向量. (3)a-b 几何作法:平移同起点,方向指向 被减数a 。 a a-b
o
b
作业: (1)课本105页第6 题
(2)同步做练习册
; / 腾讯云代理 腾讯云代理商 腾讯云服务器代理
svc81svt
一串地响了起来在这些不协调的声音中，其狐朋狗友们起身准备离开了。围堵在酒店门口的人们看到他们要走了，只给他们让开了一 条不够一人通过的小缝隙，他们只好一个接一个地侧着身子灰溜溜地挤出去走掉了。随后，那两桌衣着阔绰的外地大商人也站起来准 备走了。临走时，他们还都没有忘了对站在前台的耿正兄妹三人或拱拱手，或点点头。那些围堵在酒店门口的人看到他们出来，就让 开了更大一些的缝隙。他们也走了。90第五十二回 献艺期将满遇难坎儿|（酒店老板虽仁义，卑劣小人现丑行；兄妹献艺期将满，到 底还是遇难坎儿。）耿家兄妹仨与“盛元酒店”老板签署的三月期献艺契约眼见着就要到期了。老板提出来增加薪金续签，但耿正婉 言谢绝了。他真诚地对老板说：“非常感谢您的知遇之恩！不过，我们做完上次签的契约，就已经攒够做小生意的本钱了。在贵酒店 献艺固然不错，但我们更愿意改做生意！”这位老板人本不错，见耿正如此说，只能深表惋惜，别的也就不再说什么了。但实践已经 证明，这种拉奏演艺说唱班形式的艺人组合是非常有特色，也很吸引人的。为了确保酒店能够继续沿用这种组合形式的艺人班子，老 板就在酒店门口张贴出一张另招募一组这种艺人组合的启示。不成想，就是这个再平常不过的小小启示，却引来了一场天大的麻烦！ 说起来，出麻烦的那天距离契约期满只差一天了。那天的晚饭当口，耿正兄妹三人像往常一样有条不紊地在演唱台上拉奏演唱着。但 很快，情况就有些不对劲了：坐在台前主桌上的一个阔佬明显有意刁难，一个接一个地点一些先前不曾演唱过的怪异节目，和他同桌 吃饭的几个食客也帮着起哄，搞得整个大厅内的气氛骤然紧张起来。献艺三个月来，耿家兄妹仨第一次遭遇到了如此难以应付的尴尬 场面。酒店的伙计们原本知道这个姓吴的阔佬仗着自己很有钱，经常做一些为富不仁蛮不讲理的事情。和他同桌吃饭的几个食客都是 他的狐朋狗友，全都不是地道人儿。此时，看到形势不对劲儿了，领班的伙计头儿赶快吩咐一个机灵的小伙计去后面告知老板。听了 小伙计的述说，老板一点儿不敢怠慢，赶快整整衣冠来到前台，举止谦恭地去见那姓吴的阔佬。只见他人还没有走到那张饭桌前，就 已经开始拱手施礼了，并且以热情的笑脸连声说：“在下不知吴大员外光临，有失远迎啊，恕罪，恕罪！您也看到了，这三兄妹还年 幼呢，他们技艺不精，会演唱的曲目有限，还请大员外多多光照啊，不要难为他们！”但这蛮横的阔佬根本就不买这个账，反而傲慢 地斜眼儿瞧着谦恭的酒店老板，皮笑肉不笑地嘿嘿两声以后，这才阴阳怪气地说：“老板啊，你这个演唱班不错嘛，在咱们这个小小 的景德镇上还算有些名气呢！我嘛，实不相瞒，最近已经慕名来过你
A
. O
. N
2, 填空
AB - AD = DB BA - BC = CA
BC - BA =
OD - OA =
AC
AD
BA
OA - OB =
(3)填空
(1) (2) (3) AB - AC - CB = 0
AB + BC - AD
AB + BC - DC AB - AC + BC
=
= =
DC
AD
先复习向量的加法
b
a
a 三角形法则
-----首尾相接首到尾
平行四边形法则
----相同起点对角线
同学们学习了向量的加法，接 下来我们要学习
向量的减法
c
b
如图:
a+b= c
c-a = b
移项得:
a
c a b
这么说来，向量c与向量a进 行了减法运算，得到向量b。 像这样求两个向量的差的运 算叫做向量的减法。 那么向量的减法有什么 规律呢？
(4)
0
课堂小结:
(1)向量减法的概念.
(2)向量减法可以看作一个向量 加上另一个向量的相反向量. (3)a-b 几何作法:平移同起点,方向指向 被减数a 。 a a-b
o
b
作业: (1)课本105页第6 题
(2)同步做练习册
; / 腾讯云代理 腾讯云代理商 腾讯云服务器代理
svc81svt
一串地响了起来在这些不协调的声音中，其狐朋狗友们起身准备离开了。围堵在酒店门口的人们看到他们要走了，只给他们让开了一 条不够一人通过的小缝隙，他们只好一个接一个地侧着身子灰溜溜地挤出去走掉了。随后，那两桌衣着阔绰的外地大商人也站起来准 备走了。临走时，他们还都没有忘了对站在前台的耿正兄妹三人或拱拱手，或点点头。那些围堵在酒店门口的人看到他们出来，就让 开了更大一些的缝隙。他们也走了。90第五十二回 献艺期将满遇难坎儿|（酒店老板虽仁义，卑劣小人现丑行；兄妹献艺期将满，到 底还是遇难坎儿。）耿家兄妹仨与“盛元酒店”老板签署的三月期献艺契约眼见着就要到期了。老板提出来增加薪金续签，但耿正婉 言谢绝了。他真诚地对老板说：“非常感谢您的知遇之恩！不过，我们做完上次签的契约，就已经攒够做小生意的本钱了。在贵酒店 献艺固然不错，但我们更愿意改做生意！”这位老板人本不错，见耿正如此说，只能深表惋惜，别的也就不再说什么了。但实践已经 证明，这种拉奏演艺说唱班形式的艺人组合是非常有特色，也很吸引人的。为了确保酒店能够继续沿用这种组合形式的艺人班子，老 板就在酒店门口张贴出一张另招募一组这种艺人组合的启示。不成想，就是这个再平常不过的小小启示，却引来了一场天大的麻烦！ 说起来，出麻烦的那天距离契约期满只差一天了。那天的晚饭当口，耿正兄妹三人像往常一样有条不紊地在演唱台上拉奏演唱着。但 很快，情况就有些不对劲了：坐在台前主桌上的一个阔佬明显有意刁难，一个接一个地点一些先前不曾演唱过的怪异节目，和他同桌 吃饭的几个食客也帮着起哄，搞得整个大厅内的气氛骤然紧张起来。献艺三个月来，耿家兄妹仨第一次遭遇到了如此难以应付的尴尬 场面。酒店的伙计们原本知道这个姓吴的阔佬仗着自己很有钱，经常做一些为富不仁蛮不讲理的事情。和他同桌吃饭的几个食客都是 他的狐朋狗友，全都不是地道人儿。此时，看到形势不对劲儿了，领班的伙计头儿赶快吩咐一个机灵的小伙计去后面告知老板。听了 小伙计的述说，老板一点儿不敢怠慢，赶快整整衣冠来到前台，举止谦恭地去见那姓吴的阔佬。只见他人还没有走到那张饭桌前，就 已经开始拱手施礼了，并且以热情的笑脸连声说：“在下不知吴大员外光临，有失远迎啊，恕罪，恕罪！您也看到了，这三兄妹还年 幼呢，他们技艺不精，会演唱的曲目有限，还请大员外多多光照啊，不要难为他们！”但这蛮横的阔佬根本就不买这个账，反而傲慢 地斜眼儿瞧着谦恭的酒店老板，皮笑肉不笑地嘿嘿两声以后，这才阴阳怪气地说：“老板啊，你这个演唱班不错嘛，在咱们这个小小 的景德镇上还算有些名气呢！我嘛，实不相瞒，最近已经慕名来过你
平面向量的加减法
平面向量的加减法在学习数学的过程中，平面向量是一个非常重要的概念。
平面向量的加减法是我们在解决各种问题时必须掌握和运用的技巧。
本文将详细介绍平面向量的加减法原理、方法和应用。
一、平面向量的定义和表示方法平面向量是有大小和方向的量，通常用箭头表示。
记作AB→，其中A是向量的起点，B是向量的终点，箭头表示向量的方向。
平面向量也可以用坐标表示。
对于平面上的点A(x1，y1)和B(x2，y2)，它们之间的向量AB→的坐标表示为：AB→ = (x2 - x1, y2 - y1)二、平面向量的加法原理平面向量的加法满足以下原理：向量的加法可以看作是平移操作，将一个向量平移至另一个向量的终点，起点不变，终点变为两个向量终点相连的点。
具体来说，设有向量AB→和向量CD→，它们的和向量为EF→，则有：EF→ = AB→ + CD→三、平面向量的加法方法通过平面向量的加法原理，我们可以得到两个有向线段的和向量。
具体操作如下：1. 将两个向量的起点放在同一点上。
2. 将其中一个有向线段平移至另一个有向线段的终点。
3. 连接起点和平移后的有向线段的终点，得到和向量。
四、平面向量的减法原理平面向量的减法可以看作是加法的逆运算。
即，向量的减法可以看作是将一个向量平移至另一个向量的终点，起点不变，终点变为两个向量的起点相连的点。
具体来说，设有向量AB→和向量CD→，它们的差向量为EF→，则有：EF→ = AB→ - CD→五、平面向量的减法方法通过平面向量的减法原理，我们可以得到两个有向线段的差向量。
具体操作如下：1. 将两个向量的起点放在同一点上。
2. 将其中一个有向线段平移至另一个有向线段的终点。
3. 连接平移后的有向线段的起点和另一个有向线段的终点，得到差向量。
六、平面向量的应用平面向量的加减法在几何、物理等各个领域中都有广泛的应用。
以下是一些常见的应用示例：1. 平面向量的位移：可以用于描述物体在平面上的位移和路径。
平面向量加减法口诀
向量的加法口诀： 首尾相连，首连尾，方向指向末向量。
以第一个向量的起点为起点，以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算，图像如下图所示：向量的减法口诀： 首首相连，尾连尾，方向指向被减向量。
以第一个向量的终点为起点，以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容，要求同学们会向量的基本运算，其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算，学会运用图像解决向量加减法，向量的数乘等问题。
向量的相关题目难度也不是很大，只要大家认真学习，认真做好笔记，认真做做题目，总结做题规律，那么当我们遇到类似题目时就会似曾相识，做起来也很顺手，再细心点的话，得满分也没有问题。
学习方法很多，重要的事找到适合自己的方法，当然适合自己方法就是最好的方法。
附一；三角形定则解决向量加减的方法将各个向量依次首尾顺次相接，结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减，则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣＞1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上伸长为原来的λ∣倍；当∣λ∣＜1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律：(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律（第一分配律）：(λ+μ)a=λa+μa.数对于向量的分配律（第二分配律）：λ(a+b)=λa+λb.数乘向量的消去律：① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义：已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义：两个向量的数量积（内积、点积）是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉；若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示：a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a（交换律）；(λa)·b=λ(a·b)(关于数乘法的结合律)；（a+b)·c=a·c+b·c（分配律）；向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即：(a·b)·c≠a·(b·c)；例如：(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即：由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义：两个向量a和b的向量积（外积、叉积）是一个向量,记作a×b.若a、b不共线,则a×b的模是：∣a×b∣=|a|·|b|·sin〈a,b〉；a×b的方向是：垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质：∣a×b∣是以a和b为边的平行四边形面积.。
向量的加减法课件
题目2
已知向量$overset{longrightarrow}{a} = (2,3)$，$overset{longrightarrow}{b} = ( - 1,2)$，求$overset{longrightarrow}{a} overset{longrightarrow}{b}$。
进阶练习题
题目3
三角形法则的几何解释
向量减法的三角形法则可以理解为两个向量在起点和终点之间形成的闭合三角形，减数向量是三角形的一条边。
向量减法的向量场意义
向量场
向量场是由一组有序的向量所组成的集合，每个向量都有一个起点和一个终点。
向量场中向量的加减法
在向量场中，向量的加减法可以通过将减数的起点移动到被减数的起点来实现，然后按照向量的加法 法则进行计算。
感谢您的观看
THANKS
02 向量加法的几何意义
向量加法的平行四边形法则
总结词
向量加法的平行四边形法则是向量的基本运算法则之一，它 基于平行四边形的性质，将两个向量相加得到一个新的向量 。
详细描述
向量加法的平行四边形法则是通过构造一个平行四边形，其 中两个相邻的边分别表示要相加的向量，然后连接对角线来 表示这两个向量的和。
详细描述
在向量场中，向量加法运算可以看作 是将一个向量从一个点平移到另一个 点，这种平移过程可以用来描述物体 在空间中的运动和力的作用。
03 向量减法的几何意义
向量减法的三角形法则
三角形法则
向量减法可以通过作平行四边形并取对角线来实现，也可以通过连接两个向量的起点，并作与减数平行的向量来 实现。
答案3
$2overset{longrightarrow}{a} + overset{longrightarrow}{b} = (5,5)$
向量及其加减法,向量与数的乘法
一、向量的概念
M2
向量：既有大小又有方向的量.
向量表示：a 或 M1M2
M1
以M1为起点，M2 为终点的有向线段.
向量的模： 向量的大小.| a| 或 | M1M2 |
单位向量：模长为1的向量. a0
或
M1 M 20
零向量：模长为0的向量. 0
自由向量：不考虑起点位置的向量.
相等向量：大小相等且方向相同的向量.
证 AM MC BM MD
D b
A
a
C
M
B
AD AM MD MC BM BC
AD 与 BC 平行且相等, 结论得证.
四、小结
向量的概念（注意与标量的区别） 向量的加减法（平行四边形法则） 向量与数的乘法（注意数乘后的方向）
思考题
已知平行四边形ABCD的对角线
AC a,
BD b
10、把平行于某一直线的一切单位向量归结到共同的
11、始 要使点，a则b终点a构 b成成__立__，__向__量_a__,_b_应__满__足_____；_____
12、_要__使__a___b___a____b_成_；立，向量a,
b 应满足_______
___________ .
二、用向量方法证明：对角线互相平分的四边形是平 行四边形 .
a
b
负向量：大小相等但方向相反的向量. a
a
a
向径： 空间直角坐标系中任一点 M与原点 构成的向量.OM
二、向量的加减法
[1]
加法：a
b
c
（平行四边形法则）
b
c
a
（平行四边形法则有时也称为三角形法则）
特殊地：若 a‖
a b
M2
向量：既有大小又有方向的量.
向量表示：a 或 M1M2
M1
以M1为起点，M2 为终点的有向线段.
向量的模： 向量的大小.| a| 或 | M1M2 |
单位向量：模长为1的向量. a0
或
M1 M 20
零向量：模长为0的向量. 0
自由向量：不考虑起点位置的向量.
相等向量：大小相等且方向相同的向量.
证 AM MC BM MD
D b
A
a
C
M
B
AD AM MD MC BM BC
AD 与 BC 平行且相等, 结论得证.
四、小结
向量的概念（注意与标量的区别） 向量的加减法（平行四边形法则） 向量与数的乘法（注意数乘后的方向）
思考题
已知平行四边形ABCD的对角线
AC a,
BD b
10、把平行于某一直线的一切单位向量归结到共同的
11、始 要使点，a则b终点a构 b成成__立__，__向__量_a__,_b_应__满__足_____；_____
12、_要__使__a___b___a____b_成_；立，向量a,
b 应满足_______
___________ .
二、用向量方法证明：对角线互相平分的四边形是平 行四边形 .
a
b
负向量：大小相等但方向相反的向量. a
a
a
向径： 空间直角坐标系中任一点 M与原点 构成的向量.OM
二、向量的加减法
[1]
加法：a
b
c
（平行四边形法则）
b
c
a
（平行四边形法则有时也称为三角形法则）
特殊地：若 a‖
a b
向量的加减法及数乘运算
o·
A 的三角形法则
B
AB BC AC
ab ba (a b) c a (b c)
1． 相反向量：
与 做 记作
a长aa度的相相等反，向方量向相反的向量，叫
规定:零向量的相反向量仍是零向量。
注：（1） a a
（（32））如任即 那果意： 么，向：量aaa与, b它互a相为b,反相b向反a量向a的量a, a和，0是b零向0量. 。
a
b
D
b
由作向量差的方法，
知
DB
AB
AD
a
A b
a
C B
练习u.A如uBur图，ar ,平uAuDu行r 四br边，形你A能B用CD的、ar 两br来条表对示角线Mu相uuAr交、uM于uuBr点、uMMuuCur，和且uMuuD。ur
D
C
M
b
A
r a
B
另：（1） a b a b a b
(2)若b // a(a 0),则b a是否成立?
成立
向量共线定理：
rr r r
向量a(a 0)与b共线,当且仅当有唯一一个实数,
rr
使b a.
rr
r rr r
即a与b共线
b a (a 0)
思考:1)
r a
为什么要是非零向量?
r 2) b 可以是零向量吗?
总结:
证明三点共线的方法:
AB=λBC
uuur r r uuur r r
OB a 2b,OC a 3b. 你能判断A、B、C三点之
间的位置关系吗？为什么？
C
r
r
a
b
r 3b
B
r
2b
A
向量的各种运算及其应用
向量的各种运算及其应用随着科技的发展，向量成为了许多学科中不可或缺的重要概念，如物理、计算机科学、数学等。
向量是具有大小和方向的量，可以用于描述空间中的物理量或者图形的位置等信息。
然而，向量不仅仅是一个抽象的概念，还可以进行各种运算并应用于实际问题中。
本文将介绍向量的各种运算及其应用。
一、向量的基本运算向量的基本运算包括加法、减法、乘法。
其中，向量的加法和减法可以用直角坐标系表示，向量乘法分为数量积和叉积。
1. 向量加法和减法向量加法指的是将两个向量相加得到一个新的向量，向量加法可以表示为： A + B = C，其中 A、B、C 为向量。
向量加法可以用平行四边形法则表示，即将两个向量首尾相接，作出第三个向量，第三个向量的起点即为第一个向量的起点，终点即为第二个向量的终点。
向量减法指的是将一个向量减去另一个向量得到一个新的向量，向量减法可以表示为： A - B = C，其中 A、B、C 为向量。
向量减法可以用三角形法则表示，即将第二个向量取反，再将两个向量相加即可得到第三个向量。
2. 向量乘法向量乘法分为数量积和叉积。
数量积是指两个向量点乘而得到的一个标量，数量积可以表示为：A • B = |A| |B| cos∠(A,B)，其中 A、B 为向量，|A| 和 |B| 分别为对应向量长度，∠(A,B) 为 A、B 之间的夹角。
数量积可以用以下公式快速计算：A • B = Ax*Bx + Ay*By + Az*Bz。
叉积是指两个向量叉乘而得到的一个新的向量，叉积可以表示为：A × B = |A| |B| sin∠(A,B) n，其中 n 为符合右手定则的向量，∠(A,B) 为 A、B 之间的夹角。
叉积可以用以下公式快速计算：A× B = (AyBz − AzBy, AzBx − AxBz, AxBy − AyBx)。
二、向量的应用向量在物理、计算机科学和数学等学科中都有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
泗县三中教案、学案：向量的加减法运算 年级高一 学科数学 课题 向量的加减法运算 授课时间 撰写人 刘艳宏 时间 学习重点 用向量加减法的三角形法则和平行四边形法则，作两个向量的和与差向量 学习难点 理解向量加减法的定义. 学 习 目 标 ⑴掌握向量加法的定义 ⑵会用向量加法的三角形法则和向量的平行四边形法则作两个向量的和向量 ⑶理解向量加法的运算律
练习。设， ， ，试用 表示 .
三巩 固 练 习 1. 平行四边形 中， ， ，则 等于（ ）. A. B. C. D. 2. 下列等式不正确的是（ ）. A. B. C. D. 3.在 中， 等于（ ）. A. B. C. D. 4. = ； = . 5. 已知向量 、 满足 且 ，则 = . 6. 在 中， ，则 等于（ ）. A. B. C. D. 7. 化简 的结果等于（ ）. A. B. C. D. 8. 在正六边形 中， ， ，则 = . 9. 已知 、 是非零向量，则 时，应满足条件 .
教学 过 程 一 自 主 学 习 向量的三角形及平行四边形法则
向量的反向量
向量加法与减法的几何意义
二师 生 互动
例1如图5，O为正六边形的中心，试作出下列向量： （1） ；（2） ； （3） ； （4） ； （5） 例2 在 中， 是重心， 、 、 分别是 、 、 的中点，化简下列两式： ⑴ ； ⑵
四课 后 反 思
五课 后 巩 固 练 习 1. 已知 是 的对角线 的交点， 若 ， ， ， 试证明： .
2. 在菱形 中， ， ，求 的值.
练习。设， ， ，试用 表示 .
三巩 固 练 习 1. 平行四边形 中， ， ，则 等于（ ）. A. B. C. D. 2. 下列等式不正确的是（ ）. A. B. C. D. 3.在 中， 等于（ ）. A. B. C. D. 4. = ； = . 5. 已知向量 、 满足 且 ，则 = . 6. 在 中， ，则 等于（ ）. A. B. C. D. 7. 化简 的结果等于（ ）. A. B. C. D. 8. 在正六边形 中， ， ，则 = . 9. 已知 、 是非零向量，则 时，应满足条件 .
教学 过 程 一 自 主 学 习 向量的三角形及平行四边形法则
向量的反向量
向量加法与减法的几何意义
二师 生 互动
例1如图5，O为正六边形的中心，试作出下列向量： （1） ；（2） ； （3） ； （4） ； （5） 例2 在 中， 是重心， 、 、 分别是 、 、 的中点，化简下列两式： ⑴ ； ⑵
四课 后 反 思
五课 后 巩 固 练 习 1. 已知 是 的对角线 的交点， 若 ， ， ， 试证明： .
2. 在菱形 中， ， ，求 的值.