七年级下册第四章变量之间的关系复习总结(全)

变量之间的关系（带答案）变量之间的关系、表达⽅法复习知识要点表⽰变量的三种⽅法：列表法、解析法（关系式法）、图象法◆要点1 变量、⾃变量、因变量(1) 在⼀变化的过程中，可以取不同数值的量叫做变量，数值保持不变的量叫做常量，常量和变量往往是相对的，相对于某个变化过程。

(2) 在⼀变化的过程中，主动发⽣变化的量，称为⾃变量，⽽因变量是随着⾃变量的变化⽽发⽣变化的量。

例如⼩明出去旅⾏，路程S、速度V、时间T三个量中，速度V⼀定，路程S则随着时间T的变化⽽变化。

则T为⾃变量，路程为因变量。

◆要点2 列表法与变量之间的关系(1) 列表法是表⽰变量之间关系的⽅法之⼀，可表⽰因变量随⾃变量的变化⽽变化的情况。

(2) 从表格中获取信息，找出其中谁是⾃变量，谁是因变量。

找⾃变量和因变量时，主动发⽣变化的是⾃变量，因变量随⾃变量的增⼤⽽增⼤或减⼩◆要点3 ⽤关系式表⽰变量之间的关系(1) ⽤来表⽰⾃变量与因变量之间关系的数学式⼦，叫做关系式，是表⽰变量之间关系的⽅法之⼀。

(2) 写变化式⼦，实际上根据题意，找到等量关系，列⽅程，但关系式的写法⼜不同于⽅程，必须将因变量单独写在等号的左边。

即实质是⽤含⾃变量的代数式表⽰因变量。

(3) 利⽤关系式求因变量的值，①已知⾃变量与因变量的关系式，欲求因变量的值，实质就是求代数式的值；②对于每⼀个确定的⾃变量的值，因变量都有⼀个确定的与之对应的值。

◆要点4 ⽤图象法表⽰变量的关系(1) 图象是刻画变量之间关系的⼜⼀重要⽅式，特点是⾮常直观。

(2) 通常⽤横轴（⽔平⽅向的数轴）上的点表⽰⾃变量，⽤纵轴（竖直⽅向的数轴）上的点表⽰因变量。

(3) 从图象中可以获取很多信息，关键是找准图象上的点对应的横轴和纵轴上的位置，才能准确获取信息。

如利⽤图象求两个变量的对应值，由图象得关系式，进⾏简单计算，从图象上变量的变化规律进⾏预测，判断所給图象是否满⾜实际情景，所给变量之间的关系等。

(4) 对⽐看：速度—时间、路程—时间两图象★若图象表⽰的是速度与时间之间的关系，随时间的增加即从左向右，“上升的线段”①表⽰速度在增加；“⽔平线段”②表⽰速度不变，也就是做匀速运动，“下降的线段”③表⽰速度在减少。

数学七年级下册知识点总结之变量之间的关系变量之间的关系知识点：一理论理解1、若Y随X的变化而变化，则X是自变量 Y是因变量。

自变量是主动发生变化的量，因变量是随着自变量的变化而发生变化的量，数值保持不变的量叫做常量。

2、能确定变量之间的关系式：相关公式①路程=速度时间②长方形周长=2(长+宽)③梯形面积=(上底+下底)高2 ④本息和=本金+利率本金时间。

⑤总价=单价总量。

⑥平均速度=总路程总时间3、若等腰三角形顶角是y，底角是x，那么y与x的关系式为y=180-2x.二、列表法：采用数表相结合的形式，运用表格可以表示两个变量之间的关系。

列表时要选取能代表自变量的一些数据，并按从小到大的顺序列出，再分别求出因变量的对应值。

列表法最大的特点是直观，可以直接从表中找出自变量与因变量的对应值，但缺点是具有局限性，只能表示因变量的一部分。

三.关系式法：关系式是利用数学式子来表示变量之间关系的等式，利用关系式，可以根据任何一个自变量的值求出相应的因变量的值，也可以已知因变量的值求出相应的自变量的值。

四、图像注意：a.认真理解图象的含义，注意选择一个能反映题意的图象;b.从横轴和纵轴的实际意义理解图象上特殊点的含义(坐标)，特别是图像的起点、拐点、交点八、事物变化趋势的描述：对事物变化趋势的描述一般有两种：1.随着自变量x的逐渐增加(大)，因变量y逐渐增加(大)(或者用函数语言描述也可：因变量y随着自变量x的增加(大)而增加(大));2. 随着自变量x的逐渐增加(大)，因变量y逐渐减小(或者用函数语言描述也可：因变量y随着自变量x的增加(大)而减小).注意：如果在整个过程中事物的变化趋势不一样，可以采用分段描述.例如在什么范围内随着自变量x的逐渐增加(大)，因变量y逐渐增加(大)等等.九、估计(或者估算) 对事物的估计(或者估算)有三种：1.利用事物的变化规律进行估计(或者估算).例如：自变量x每增加一定量，因变量y的变化情况;平均每次(年)的变化情况(平均每次的变化量=(尾数-首数)/次数或相差年数)等等;2.利用图象：首先根据若干个对应组值，作出相应的图象，再在图象上找到对应的点对应的因变量y的值;3.利用关系式：首先求出关系式，然后直接代入求值即可.拓展：数学学习技巧一、课内重视听讲，课后及时复习。

变量之间的关系知识点及常见题型一、基础知识1、常量：在一组数据中或者关系式中不会没发生变化的量；2、变量：变化的量（1）自变量：可以自己发生变化的量；（2）因变量：随自变量的变化而变化的量。

二、表示方式1、表格（1）借助表格可以感知因变量随自变量变化的情况；（2）从表格中可以获取一些信息，能够做出某种预测或估计； 2、关系式（1）能根据题意列简单的关系式； （2）能利用关系式进行简单的计算； 3、图像（1）识别图像是否正确；（2）利用图像尽可能地获取自变量因变量的信息。

第一节 小车下滑的时间课前引入1.小张从学校给妈妈打电话，在这个过程中，打电话的时间越长，电话费就越（ ）。

2.银行的年利率是2.25%，存入的本金越多，（ ）也越多，在这个问题中，（ ）是固定不变的。

（ ）随（ ）的改变而改变。

3.球的体积V 与球的半径的关系式V=34πr 3中，（ ）是一个定值。

（ ）随（ ）的改变而改变。

经典例题下表是某同学做“观察水的沸腾”实验时所记录的数据：（1）时间为8分钟时，水的温度是多少？（2）上表反应了哪两个变量之间的关系？哪个是自变量？哪个是因变量？ （3）水的温度是怎样随时间变化的？（4）根据表格，你认为13分钟、14分钟时水的温度是多少？（5）为了节约能源，在烧开水时，你认为应在几分钟左右关闭煤气？过手练习1、明明从广州给远在上海的爷爷打电话，电话费随着时间的变化而变化，在这个过程中，因变量是（）A、明明B、电话费C、时间D、爷爷2上述问题中，第五排、第六排分别有个、个座位；第排有个座位.3、据世界人口组织公布，地球上的人口从1600年到1999年一直呈递增趋势，即随时间的变化，地球上的人口数量在逐渐地增加，如果用t表示时间，y表示人口数量，是自变量，是因变量。

（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）随着自变量的变化,因变量变化的趋势是什么?（3）你认为入学儿童的人数会变成零吗?5、心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间有如下关系（其中0≤x≤30）（1）上表中反映了哪两个变量之间的关系？那个是自变量？哪个是因变量？（2）当提出概念所用时间是10分钟时，学生的接受能力是多少？（3）根据表格中的数据，你认为提出概念几分钟时，学生的接受能力最强？（4）从表格中可知，当时间x在什么范围内，学生的接受能力逐步增强？当时间x在什么范围内，学生的接受能力逐步降低？（5）根据表格大致估计当时间为23分钟时，学生对概念的接受能力是多少？第二节 变化中的三角形课前引入1.计划购买40元的某种文化用品，则所购买的总数N （个）和单价想X （元）的关系式为（ ）。

变量之间的关系、表达方法复习知识要点表示变量的三种方法：列表法、解析法（关系式法）、图象法(1) 在一变化的过程中，可以取不同数值的量叫做变量，数值保持不变的量叫做常量，常量和变量往往是相对的，相对于某个变化过程。

(2) 在一变化的过程中，主动发生变化的量，称为自变量，而因变量是随着自变量的变化而发生变化的量。

例如小明出去旅行，路程S、速度V、时间T三个量中，速度V一定，路程S则随着时间T的变化而变化。

则T为自变量，路程为因变量。

◆要点2 列表法与变量之间的关系(1) 列表法是表示变量之间关系的方法之一，可表示因变量随自变量的变化而变化的情况。

(2) 从表格中获取信息，找出其中谁是自变量，谁是因变量。

找自变量和因变量时，主动发生变化的是自变量，因变量随自变量的增大而增大或减小◆要点3 用关系式表示变量之间的关系(1) 用来表示自变量与因变量之间关系的数学式子，叫做关系式，是表示变量之间关系的方法之一。

(2) 写变化式子，实际上根据题意，找到等量关系，列方程，但关系式的写法又不同于方程，必须将因变量单独写在等号的左边。

即实质是用含自变量的代数式表示因变量。

(3) 利用关系式求因变量的值，①已知自变量与因变量的关系式，欲求因变量的值，实质就是求代数式的值；②对于每一个确定的自变量的值，因变量都有一个确定的与之对应的值。

◆要点4 用图象法表示变量的关系(1) 图象是刻画变量之间关系的又一重要方式，特点是非常直观。

(2) 通常用横轴（水平方向的数轴）上的点表示自变量，用纵轴（竖直方向的数轴）上的点表示因变量。

(3) 从图象中可以获取很多信息，关键是找准图象上的点对应的横轴和纵轴上的位置，才能准确获取信息。

如利用图象求两个变量的对应值，由图象得关系式，进行简单计算，从图象上变量的变化规律进行预测，判断所給图象是否满足实际情景，所给变量之间的关系等。

(4) 对比看：速度—时间、路程—时间两图象★若图象表示的是速度与时间之间的关系，随时间的增加即从左向右，“上升的线段”①表示速度在增加；“水平线段”②表示速度不变，也就是做匀速运动，“下降的线段”③表示速度在减少。

变量之间的关系复习变量之间的关系、表达方法知识要点表示变量的三种方法：列表法、解析法（关系式法）、图象法◆要点1 变量、自变量、因变量(1) 在一变化的过程中，可以取不同数值的量叫做变量，数值保持不变的量叫做常量，常量和变量往往是相对的，相对于某个变化过程。

(2) 在一变化的过程中，主动发生变化的量，称为自变量，而因变量是随着自变量的变化而发生变化的量。

例如小明出去旅行，路程S、速度V、时间T三个量中，速度V一定，路程S则随着时间T 的变化而变化。

则T为自变量，路程为因变量。

◆要点2 列表法与变量之间的关系(1) 列表法是表示变量之间关系的方法之一，可表示因变量随自变量的变化而变化的情况。

(2) 从表格中获取信息，找出其中谁是自变量，谁是因变量。

找自变量和因变量时，主动发生变化的是自变量，因变量随自变量的增大而增大或减小◆要点3 用关系式表示变量之间的关系(1) 用来表示自变量与因变量之间关系的数学式子，叫做关系式，是表示变量之间关系的方法之一。

(2) 写变化式子，实际上根据题意，找到等量关系，列方程，但关系式的写法又不同于方程，必须将因变量单独写在等号的左边。

即实质是用含自变量的代数式表示因变量。

(3) 利用关系式求因变量的值，①已知自变量与因变量的关系式，欲求因变量的值，实质就是求代数式的值；②对于每一个确定的自变量的值，因变量都有一个确定的与之对应的值。

◆要点4 用图象法表示变量的关系(1) 图象是刻画变量之间关系的又一重要方式，特点是非常直观。

(2) 通常用横轴（水平方向的数轴）上的点表示自变量，用纵轴（竖直方向的数轴）上的点表示因变量。

(3) 从图象中可以获取很多信息，关键是找准图象上的点对应的横轴和纵轴上的位置，才能准确获取信息。

如利用图象求两个变量的对应值，由图象得关系式，进行简单计算，从图象上变量的变化规律进行预测，判断所給图象是否满足实际情景，所给变量之间的关系等。

(4) 对比看：速度—时间、路程—时间两图象★若图象表示的是速度与时间之间的关系，随时间的增加即从左向右，“上升的线段”①表示速度在增加；“水平线段”②表示速度不变，也就是做匀速运动，“下降的线段”③表示速度在减少。

第四章变量之间的关系一、变量、自变量、因变量1、在某一变化过程中，不断变化的量叫做变量。

2、如果一个变量y随另一个变量x的变化而变化，则把x叫做自变量，y叫做因变量。

3、自变量与因变量的确定：（1）自变量是先发生变化的量；因变量是后发生变化的量。

（2）自变量是主动发生变化的量，因变量是随着自变量的变化而发生变化的量。

（3）利用具体情境来体会两者的依存关系。

二、表格1、表格是表达、反映数据的一种重要形式，从中获取信息、研究不同量之间的关系。

（1）首先要明确表格中所列的是哪两个量；（2）分清哪一个量为自变量，哪一个量为因变量；（3）结合实际情境理解它们之间的关系。

2、绘制表格表示两个变量之间关系（1）列表时首先要确定各行、各列的栏目；（2）一般有两行，第一行表示自变量，第二行表示因变量；（3）写出栏目名称，有时还根据问题内容写上单位；（4）在第一行列出自变量的各个变化取值；第二行对应列出因变量的各个变化取值。

（5）一般情况下，自变量的取值从左到右应按由小到大的顺序排列，这样便于反映因变量与自变量之间的关系。

三、关系式1、用关系式表示因变量与自变量之间的关系时，通常是用含有自变量（用字母表示）的代数式表示因变量（也用字母表示），这样的数学式子（等式）叫做关系式。

2、关系式的写法不同于方程，必须将因变量单独写在等号的左边。

3、求两个变量之间关系式的途径：（1）将自变量和因变量看作两个未知数，根据题意列出关于未知数的方程，并最终写成关系式的形式。

（2）根据表格中所列的数据写出变量之间的关系式；（3）根据实际问题中的基本数量关系写出变量之间的关系式；（4）根据图象写出与之对应的变量之间的关系式。

4、关系式的应用：（1）利用关系式能根据任何一个自变量的值求出相应的因变量的值；（2）同样也可以根据任何一个因变量的值求出相应的自变量的值；（3）根据关系式求值的实质就是解一元一次方程（求自变量的值）或求代数式的值（求因变量的值）。

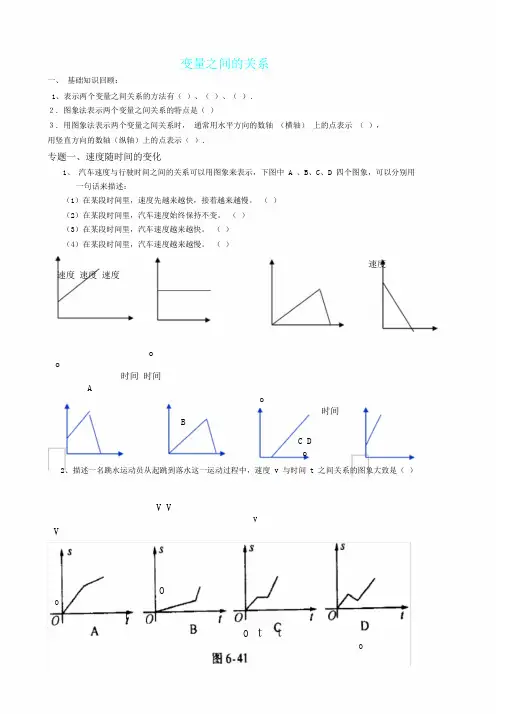
变量之间的关系一、基础知识回顾：1、表示两个变量之间关系的方法有（）、（）、（）．２．图象法表示两个变量之间关系的特点是（）３．用图象法表示两个变量之间关系时，通常用水平方向的数轴（横轴）上的点表示（），用竖直方向的数轴（纵轴）上的点表示（）．专题一、速度随时间的变化1、汽车速度与行驶时间之间的关系可以用图象来表示，下图中 A 、B、C、D 四个图象，可以分别用一句话来描述：（1）在某段时间里，速度先越来越快，接着越来越慢。

（）（2）在某段时间里，汽车速度始终保持不变。

（）（3）在某段时间里，汽车速度越来越快。

（）（4）在某段时间里，汽车速度越来越慢。

（）速度速度速度速度oo时间时间Ao时间BC Do2、描述一名跳水运动员从起跳到落水这一运动过程中，速度 v 与时间 t 之间关系的图象大致是（）V VVVOOｔO ｔｔO3、李明骑车上学，一开始以某一速度行进，途中车子发生故障，只好停下修车，车修好后，因怕耽误时间，于是加快了车速．如用 s 表示李明离家的距离， t 为时间．在下面给出的表示 s 与 t 的关系图 6—41 中，符合上述情况的是 ( )14、一辆轿车在公路上行驶，不时遇到各种情况，速度随之改变，先加速，再匀速又遇到情况而减速，过后再加速然后匀速，下公路、上小路，到达目的地．图6— 43 哪幅图象可近似描述上面情况 ( )5、“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉。

当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点⋯⋯ .用 S1、S2 分别表示乌龟和兔子所行的路程， t为时间，则下列图象中与故事情节相吻合的是（）s S1s S1 s S1s S1S2S2 S2 S2 tA B t tC D t6、星期天晚饭后，小红从家里出发去散步，下图描述了她散步过程中离家的距离 s（米）与散步所用的时间t （分）之间的关系，依据图象下面描述符合小红散步情景的是（）A. 从家出发，到了一个公共阅读报栏，看了一会儿报，就回家了 .B. 从家出发，到了一个公共阅报栏，看了一会儿报，继续向前走了一段后，然后回家了 .C. 从家里出发，一直散步（没有停留），然后回家了 D.从家里出发，散了一会儿步，就找同学去了， 18 分钟后才开始返回 .7、A、B 两地相距 500 千米，一辆汽车以 50 千米 /时的速度由 A 地驶向 B 地. 汽车距 B 地的距离 y( 千米 ) 与行驶时间t( 之间) 的关系式为. 在这个变化过程中，自变量是，因变量是 .8、下表是春汛期间某条河流在一天中涨水情况记录表格：时间/时0 4 8 12 16 20 24超警戒水位 /米⑴时间从 0时变化到 24时，超警戒水位从上升到 ;⑵借助表格可知，时间从到水位上升最快2某机动车辆出发前油箱中有油 42 升，行驶若干小时后，在途中加油站加油若干 .油箱中余油量 Q(升)与行驶时间 t(时) 之间的关系如图，请根据图像填空：⑴机动车辆行驶了小时后加油 .⑻中途·42·36·30·24Q/升·18·12·6 ·········1 2 3 4 5 6 7 8 9··10 11t/时加油升.⑵加油后油箱中的油最多可行驶小时 .⑶如果加油站距目的地还有 230 公里，机动车每小时走 40 公里，油箱中的油能否使机动车到达目的地？答：。

变量之间的关系单元知识总结及典型例题1.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度y 与所挂物体的质量x的一组对应值：所挂重量x(kg)012345弹簧长度y(cm)202224262830(1)上述表格反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？(2)当所挂重物为4kg时,弹簧多长？不挂重物呢？⑶假设所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗分析抓住表格中的对应数据,找出变量之间的规律.解(1)弹簧长度y,物体重量x是变量,物体重量是自变量,弹簧长度是因变量; (2)当所挂重物为4kg时,弹簧长度为28cm,不挂重物时弓t簧长度为20cm；⑶当所挂重物为6kg时,弹簧长度为32cm.2.如图6—1所示,梯形上底的长是x,下底的长是15,高是8.图6.1(1)梯形面积y与上底长x之间的关系式是什么？(2)用表格表示当x从10变到20时(每次增加1), y的相应值;⑶当x每增加1时,y如何变化？说说你的理由；(4)当x=0时,y等于什么？此时它表示的是什么？分析(1)根据梯形面积公式可推出y与x的关系式；(2)通过计算列表说明；(3)由表格中的数据可以观察出；(4)当上底为零时(即成为一个点),成为三角形.〜 1解(1) y — x 15 8,2即y=4x+60 ;(2)x IO11121314151617181920y100104108112116120124128132136140(3)当x每增加1时,y的值随之增加4;(4)当x=0时,y=60,此时梯形成为了三角形.3.地壳的厚度约为8到40km.在地表以下不太深的地方,温度可按y=35x+t计算,其中x是深度(km) , t是地球外表温度(C) , y是所达深度的温度(C ).(1)在这个变化过程中,自变量、因变量各是什么？(2)分别计算当x为lkm, 5km, 10km,20km时地壳的温度(地表温度为2C).解(1)自变量是深度,因变量是温度；(2)当x=1km时,y=35x+t=35x X 1+2=37( C)；当x=5km 时,y=35x+t=35 X 5+2=177( C )；当 x=10km 时,y=35x+t=35 X 10+2=352( C)； 当 x=20km 时,y=35x+t=35 X 20+2=702( C).说明 初步体会自变量和因变量的数值对应关系,能由自变量的值求得因变量的值. 题型发散发散1选择题 把正确答案的代号填入题中的括号内.(1)下面的图表列出了一项试验的统计数据,表示将皮球从高处 d 落下时,弹跳高度 b 与下落高度d 的关系.试问,下面的哪个式子能表示这种关系 (单位：cm)()d50 80 100 150 b254050752____d _ _(A) b d (B)b=2d (C) b —(D)b=d+252(2)某地一天的气温随时间的变化如图 6— 2,根据图象可知：在这一天中最高气温与到达最高气温的时刻分别是 ()因上述数字完全与表格中的数字符合. 故此题应选(C). (2)用直接法.由图6 —2知一天到达最高气温 12c 的时间是14时. 故此题应选(C). 发散2填空题如图6—3, △ ABC 是等腰三角形,周长是 60cm,腰为xcm,底为ycm.(A)14C; 12h (B)4 解(1)用验证法. d 当 d=50 时,b — 2 d当 d=80 时,b d2d 当 d=100 时,b —2 一 d 当 d=150 时,b d 2C; 50 280 21002150 22h25406 2(C)12 C; 14h (D)2 C; 4h50 ；75.2 4 6 R 12 崎 16 Ifl 30 22 24 Hh)141210 g6A(1)写出用含x的关系式来表示y;(2)当腰由20cm变化到25cm时,底边长由cm变化到cm；(3)腰为20cm时,是什么形状的三角形？假设腰为30cm时,行吗？分析三角形的周长是三条边长的和.解：(1)y=60-2x ;(2)底边由20cm变化到10cm；(3)当腰为20cm时,是等边三角形,假设腰为30cm,那么无法形成三角形.纵横发散发散1南京市在某一天的地表气温是38C,据测量每升高1km,气温下降6C,那么在hkm的高空,温度t是多少？并计算当h的值是6km. 10km 12km时的气温.讨论一下民用飞机在一万米高空飞行时,机舱为什么要与机外空气隔绝？分析用含h的代数式来表示气温.解：t=38-6h .当h=6 时,t=2 C；当h=10 时,t=-22 C；当h=12 时,t=-34 C.原因有很多,其中一点是机舱外温度非常低.发散2婴儿在6个月、一周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁时的2倍、3倍.(1)上述哪些量在发生变化？自变量和因变量各是什么？(2)某婴儿在出生时的体重是 3.5kg,请把他在发育过程中的体重情况填入: 年龄刚出生6个月1周岁2周岁6周岁10周岁体重(kg)⑶根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的解：(1)年龄和体重都在变化；年龄是自变量,体重是因变量；(2)年龄刚出生6个月1周岁2周岁6周岁10周岁体重(kg) 3.57.010.014.521.531.5转化发散发散1图6 — 4是某地一天的气温随时间变化的图象.根据图象答复,在这一天中:(1)什么时间气温最高？什么时间气温最低？最高气温和最低气温各是多少？(2)20时的气温是多少？(3)什么时间的气温为 6C? (4)哪段时间内气温不断下降 ？ (5)哪段时间内气温持续不变？图63解：(1)凌晨4时,气温最低,气温是 -4C; 16时气温最高,气温是 10C; (2)20时的气温是8C;(3)10时和22时的气温都是6C ；(4)0时到4时和16时到24时这两段时间内气温不断下降； (5)12时到14时这两个小时内气温保持 8c 的温度不变.解法指导(1)气温最低、最高反映在图象上就是找最低点和最高点；(2)20时的气温是多少,实质上是求当t=20时,T=?(3)什么时间的气温为 6C,实质上是求当 T=6C 时,t=?直线T=6与图象交于两点,因此 t=10或t=22 ;(4)图中共有两段时间气温不断下降,不可遗漏；(5)气温保持不变,指的是 T 值保持不变,图中只有 t 在12h 到14h 这两个小时满足条件. 发散2为了增强公民的节水和用水意识,合理利用水资源,各地采用价风格控等手段到达节约用水的目的.某市规定如下用水收费标准：每户每月的用水不超过 6m 3时,水费按每立方米 a 元收费； 超过6m 3时,不超过的局部每立方米仍按 a 元收费,超过的局部每立方米按 c 元收费.该市某户今年 3、4月份的用水量和水费如下表所示：月份 用水量(m3)水费(元) 35 7.5 4927设某户该月用水量为x m 3 ,应交水费为y (元). (1)求a 、c 的值,并写出用水不超过 6m 3和超过6m 3时,y 与x 之间的关系式;(2)假设该户5月份的用水量为8m 3,求该户5月份的水费是多少元 ？解：(1)依题意,有： 当 x w 6 时,y=ax; 当 x>6 时,y=6a+c(x-6). 1.5 6y=1.5x(x < 6),y=9+6(x-6)=6x-27(x>6) (2)将 x=8 代人 y=6x-27(x>6), y=6X 8-27=21(元). 答：t ^户5月份的水费是21元.发散3如图6—5所示的曲线表示某人骑一辆自行车时离家的距离与时间的关系.骑车者九点离 开家,十五点回家.根据这个曲线图,答复以下问题：由,得7.5 5a 27 6a 3c 解得■距寓(km)期6-5(1)到达离家最远的地方是什么时间？离家多远？(2)何时开始第一次休息？休息多长时间？(3)第一次休息时离家多远？(4)11:00到12:00他骑了多少千米？(5)他在9:00至IJ 10:00和10:00至IJ 10:30的平均速度是多少？(6)他在何时至何时停止前进并休息用午餐？(7)他在停止前进后返回,骑了多少千米？返回时的平均速度是多少？解(1)到达离家最远的地方的时间是12时,离家30km；(2)10.5 时开始第一次休息,休息了0.5h ;⑶第一次休息时离家17.5km；(4)11:00 到12:00 ,他骑了12.5km；(5)9:00 到10:00的平均速度是lOkm/h, 10:00到10:30的平均速度是15km/h;(6)从12:00到13:00间停止前进,并休息用午餐较为符合实际情况；(7)他在停止前进后返回,骑了30km,共用了2h,故返回时的平均速度是15km/h.知识整合网络【学习方法指导】量与量之间存在着相互影响的关系,本章通过丰富的现实情境引入变量对变量之间关系的讨论, 使学生体验探索和表示变量之间关系的过程,获得对表格、关系式、图象等多种方法的熟悉,能读懂表格、关系式、图象所表示的信息,能用自己的语的描述表格、关系式和图象所表示的关系,并能预测.关系式是表示变量之间关系的另一种方法.利用关系式,可以依据任何一个自变量的值求出相应的因变量的值.也可以依据因变量的值求出相应的自变量的值^由学习常量问题转入学习变量问题,这是数学思维的一种跃升,引导我们前进的是一种崭新的思 维方式. 【中考信息传递】近年来全国各省、市中考题中涉及本章内容的题型多为选择题、填空题,也有局部的应用题及因 变量关于自变量的关系式的中档题,应该充分重视.【中考名题赏析】 题型发散 发散1填空题(1)观察以下图形(图6—24),假设第①个图形中阴影局部的面积为 1,第②个图形中阴影局部的面• 3 一 . ..... ............. . - 9— . .......... ... • 27 一 … .一. 积为3,第③个图形中阴影局部的面积为第④个图形中阴影局部的面积为 27 ,…那么第n 个图形416 64中阴影局部的面积为 (用字母n 表示)(2002年潍坊市中测试题第2块图形的面积为第3块图形的面积为第4块图形的面积为 第n 块图形的面积为 (2)如图6—25,观察以下三角形图案,每行圆点的个数有什么规律 代数式表示这两个三角形图案中圆点的总数,为(2002年广西壮族自治区中测试题图 6-25解第1行圆点个数为1+n, 第2行圆点个数为2+(n-1)=1+n ,C 3 1394 164 1327 4 64n 134?设每个三角形有n 行,用n 的 解由于第1块图形的面积为1,2 1第3行圆点个数为3+(n-2)=1+n ,第n行圆点的个数为n+1.以上共有n行,故这两个三角形图案中圆点的总数为n(n+1)个.发散2解做题如图6—26表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象为正比例函数和一次函数).两地间的距离是80km.请你根据图象答复或解决下面的问题：SI 6-26(1)谁出发的较早？早多长时间徘到达乙地较早？早到多长时间？(2)两人在途中行驶的速度分别是多少？(3)请你分别求出表示自行车和摩托车行驶过程的函数解析式(4)指出在什么时间段内两车均行驶在途中(不包括端点)；在这一时间段内,请你分别按以下条件列出关于时间x的方程或不等式(不要化简,也不要求解)：①自行车行驶在摩托车前面；②自行车与摩托车相遇；③自行车行驶在摩托车后面.解(1)由图可以看出：自行车出发较早,早3h;摩托车到达乙地较早,早3h.(2)对自行车而言：彳T驶的距离是80km,耗时8h,所以其速度是：80+8=10(km/h);对摩托车而言：行驶的距离是80km,耗时2h,所以其速度是：80+2=40(km/h).(3)设表示自行车行驶过程的函数解析式为:. x=8 时,y=80,.•-80=8k,解得k=10,・♦・表示自行车行驶过程的函数解析式为设表示摩托车行驶过程的函数解析式为. x=3 时,y=0,而且x=5 时,y=80;0 3ab a 40.•,解得80 5ab b 120••表示摩托车行驶过程的函数解析式为(4)在3Vx<5时间段内两车均行驶在途中①自行车在摩托车前面：10x>40x-120,②两车相遇：10x=40x-120,③自行车在摩托车后面：10x<40x-120. y=40x-120 .(分别h)(不要求写出自变量的取值范围)；y=kx,y=10x;y=ax+b,。