应用Dijkstra算法求赋权图最短路径

在交通网络中，常常会提出许多这样的问题：两地之间是否有路相通？在有多条通路的情况下，哪一条最近？哪一条花费最少等。

交通网络可以用带权图表示，图中顶点表示域镇，边表示两城之间的道路，边上权值可表示两城镇间的距离，交通费用或途中所需的时间等。

以上提出的问题就是带权图中求最短路径的问题，即求两个顶点间长度最短的路径。

最短路径问题的提法很多。

在这里仅讨论单源最短路径问题：即已知有向图(带权)，我们希望找出从某个源点S∈V到G中其余各顶点的最短路径。

例如：下图(有向图G14)，假定以v1为源点，则其它各顶点的最短路径如下表所示：图G14从有向图可看出，顶点v1到v4的路径有3条：(v1,v2,v4)，(v1,v4)，(v1,v3,v2,v4)，其路径长度分别为：15,20和10。

因此v1到v4的最短路径为(v1,v3,v2,v4 )。

为了叙述方便，我们把路径上的开始点称为源点，路径的最后一个顶点为终点。

那么，如何求得给定有向图的单源最短路径呢？迪杰斯特拉(Dijkstra)提出按路径长度递增产生诸顶点的最短路径算法，称之为迪杰斯特拉算法。

迪杰斯特拉算法求最短路径的实现思想是：设有向图G=(V,E)，其中，V={0,2,…,n-1}，cost是表示G的邻接矩阵，G.arcs [i][j] .adj 表示有向边<i,j>的权。

若不存在有向边<i,j>，则G.arcs [i][j] .adj 的权为无穷大(这里取值为32767)。

设S是一个集合，其中的每个元素表示一个顶点，从源点到这些顶点的最短距离已经求出。

设顶点v0为源点，集合S的初态只包含顶点v0。

数组D记录从源点到其他各顶点当前的最短距离，其初值为D[i]= G.arcs[v0][i].adj ，i=1,…,n-1。

从S之外的顶点集合V-S 中选出一个顶点w，使D[w]的值最小。

于是从源点到达w只通过S 中的顶点，把w加入集合S中调整D中记录的从源点到V-S中每个顶点v的距离：从原来的D[v] 和D[w]+ G.arcs [w][v] .adj中选择较小的值作为新的D[v]。

dijkstra算法城市最短路径问题Dijkstra算法是一种经典的图算法，用于求解带有非负权重的图的单源最短路径问题。

在城市的交通规划中，Dijkstra算法也被广泛应用，可以帮助我们找到最短的路线来节省时间和成本。

一、最短路径问题的定义最短路径问题，指的是在一个带权重的有向图中，找到从起点到终点的一条路径，它的权重之和最小。

在城市的交通规划中，起点和终点可以分别是两个街区或者两个交通枢纽。

二、Dijkstra算法Dijkstra算法是基于贪心策略的一种算法，用于解决带非负权重的最短路径问题。

它采用了一种贪心的思想：每次从起点集合中选出当前距离起点最近的一个点，把其移到已知的最短路径集合中。

并以该点为中心，更新它的相邻节点的到起点的距离。

每次更新距离时，选择距离起点最近的距离。

三、Dijkstra算法实现1. 创建一个到起点的距离数组和一个布尔类型的访问数组。

2. 将起点的到起点的距离设置为0，其他的节点设置为无穷大。

3. 从距离数组中选择没有访问过且到起点距离最近的点，将它标记为“已访问”。

4. 对于它的所有邻居，如果出现路径缩短的情况，就更新它们的距离。

5. 重复步骤3和4，直到所有节点都被标记为“已访问”。

6. 最后，根据到起点的距离数组，以及每个节点的前驱节点数组，可以得到从起点到终点的最短路径。

四、Dijkstra算法的时间复杂度Dijkstra算法的时间复杂度可以通过堆优化提高，但最坏情况下时间复杂度仍达到O(ElogV)。

其中，E是边的数量，V是顶点的数量。

因此，Dijkstra算法在不考虑空间复杂度的情况下，是一种高效且实用的解决城市最短路径问题的算法。

五、结论Dijkstra算法是一个广泛应用于城市交通规划领域的算法，可以帮助我们找到最优的路线来节省时间和成本。

它基于贪心策略，每次从起点集合中选择距离起点最近的点，并对其邻居节点进行松弛操作。

Dijkstra算法的时间复杂度虽然较高，但堆优化可以提高算法性能。

dijkstra最短路径算法详解
Dijkstra最短路径算法是一种常用的图算法，用于求解带权图中的单源最短路径问题，即从一个固定的源节点到图中的其他节点的最
短路径。

以下是详细的算法步骤：
1. 初始化
一开始，将源节点的距离设为0，其余节点的距离设置为正无穷，在未访问的节点集合中把源节点压入堆中。

2. 确定最短路径
从堆中取出未访问节点集合中距离源节点最近的节点v，标记其
为已访问。

之后，对于v的邻居节点w，计算从源节点到v再到w的距离，如果经过v的路径比已经计算得到的路径短，则更新路径。

更新
后的距离先暂时放入堆中，如果后边有更短的路径，则更新。

3. 重复第2步
重复第2步，直到取出的节点为终点节点，或者堆为空。

4. 算法结束
算法结束后，各节点的距离就是从源节点到它们的最短距离。

Dijkstra算法的复杂度是O(NlogN)，其中N是节点个数。

其优
势在于只需要算一次即可得到所有最短路径，但是要求所有边的权值
必须非负，否则会导致算法不准确。

总之，Dijkstra算法是一种简单有效的最短路径算法，其实现也比较直观。

在处理如飞机和火车等交通路径规划问题中有较好的应用。

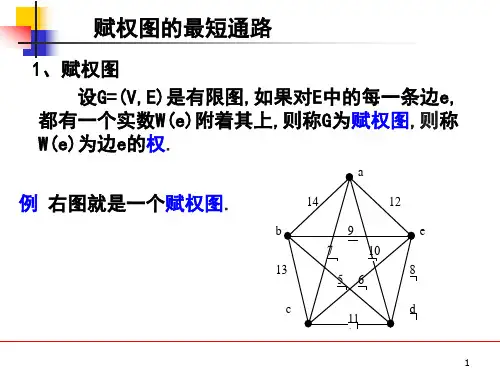
最短路径dijkstra算法例题最短路径问题是图论中的一个重要问题，它的解决方法有很多种，其中最著名的算法之一就是Dijkstra算法。

本文将介绍Dijkstra算法的基本思想和实现过程，并通过一个例题来展示其具体应用。

一、Dijkstra算法的基本思想Dijkstra算法是一种贪心算法，它以起点为中心向外扩展，每次选择当前距离起点最短的点作为下一个扩展点，并更新其周围节点到起点的距离。

这个过程不断重复直至所有节点都被扩展完毕。

具体实现时，可以使用一个数组dist来存储每个节点到起点的距离，初始时所有节点到起点的距离都设为无穷大（表示不可达），起点到自己的距离设为0。

同时还需要使用一个visited数组来记录每个节点是否已经被扩展过。

在每次扩展时，从未被扩展过且与当前扩展节点相邻的节点中选择距离起点最短的节点作为下一个扩展节点，并更新其周围节点到起点的距离。

这个过程可以使用优先队列来实现。

二、Dijkstra算法实现例题下面我们通过一个例题来演示Dijkstra算法的具体实现过程。

例题描述：给定一个有向带权图，求从起点s到终点t的最短路径。

解题思路：根据Dijkstra算法的基本思想，我们可以使用一个优先队列来实现。

具体实现步骤如下：1. 初始化dist数组和visited数组。

2. 将起点s加入优先队列，并将其距离起点的距离设为0。

3. 重复以下步骤直至优先队列为空：（1）取出优先队列中距离起点最近的节点u。

（2）如果该节点已经被扩展过，则跳过此节点，否则将其标记为已扩展。

（3）如果该节点就是终点t，则返回其到起点的距离。

（4）否则，遍历该节点的所有邻居节点v，并更新它们到起点的距离。

如果某个邻居节点v之前未被扩展过，则将其加入优先队列中。

更新dist[v]后，需要将v加入优先队列中以便后续扩展。

4. 如果经过以上步骤仍然没有找到终点t，则表示不存在从起点s到终点t的路径。

代码实现：```#include <iostream>#include <queue>#include <vector>using namespace std;const int INF = 0x3f3f3f3f;const int MAXN = 1005;int n, m, s, t;int dist[MAXN], visited[MAXN];vector<pair<int, int>> graph[MAXN];void dijkstra() {priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;pq.push(make_pair(0, s));dist[s] = 0;while (!pq.empty()) {pair<int, int> p = pq.top();pq.pop();int u = p.second;if (visited[u]) {continue;}visited[u] = 1;if (u == t) {return;}for (int i = 0; i < graph[u].size(); i++) {int v = graph[u][i].first;int w = graph[u][i].second;if (!visited[v] && dist[v] > dist[u] + w) {dist[v] = dist[u] + w;pq.push(make_pair(dist[v], v));}}}}int main() {cin >> n >> m >> s >> t;for (int i = 1; i <= m; i++) {int u, v, w;cin >> u >> v >> w;graph[u].push_back(make_pair(v, w));}memset(dist, INF, sizeof(dist));memset(visited, 0, sizeof(visited));dijkstra();if (dist[t] == INF) {cout << "No path from " << s << " to " << t << endl;} else {cout << "Shortest path from " << s << " to " << t << ": " << dist[t] << endl;}}```代码解析：首先定义了一些常量和全局变量，其中n表示节点数，m表示边数，s 表示起点，t表示终点。

《求解最短路径：应用迪杰斯特拉算法》一、介绍Dijkstra算法的概念和基本原理Dijkstra算法是一种用于解决最短路径问题的算法，它由荷兰计算机科学家Edsger Dijkstra在1959年发明，用于求解从源点到其他所有结点的最短路径。

它的基本原理是：在一张图中，从源点到每一个结点的最短路径是从源点开始，经过最少的边到达每一个结点的路径。

Dijkstra算法的实现过程中，首先要建立一个有向图，该图由顶点和边组成，每条边都有一个权值，表示从一个顶点到另一个顶点的距离。

然后，从源点开始，每次选择最小权值的边，继续查找下一个顶点，直到找到终点。

最后，将所有路径之和求出，即为源点到目标点的最短路径。

举例来说，假如有一张有向图，其中有A，B，C，D四个结点，以及AB，AC，BD，CD四条边，其中AB，AC，BD边的权值分别为2，3，1，CD边的权值为4。

如果要求求出从A到D的最短路径，则可以使用Dijkstra算法，首先从A出发，选择权值最小的边，即BD，则A-B-D的路径长度为3，接着从B出发，选择权值最小的边，即CD，则A-B-D-C的路径长度为7，因此，从A到D的最短路径为A-B-D，路径长度为3。

Dijkstra算法的优点是算法简单，实现方便，时间复杂度低，它可以用于解决路径规划，车辆调度，网络路由等问题，同时，它也可以用于解决复杂的最短路径问题。

因此，Dijkstra算法在计算机科学中有着重要的应用价值。

二、讨论Dijkstra算法的应用及其优势Dijkstra算法是一种用于解决最短路径问题的算法，它的应用和优势非常广泛。

首先，Dijkstra算法可以用于解决交通路网中的最短路径问题。

例如，在一个城市的交通路网中，如果一个乘客要从一个地方到另一个地方，那么他可以使用Dijkstra算法来查找最短的路径。

这样可以节省乘客的时间和金钱，也可以减少拥堵。

此外，Dijkstra算法还可以用于解决计算机网络中的最短路径问题。

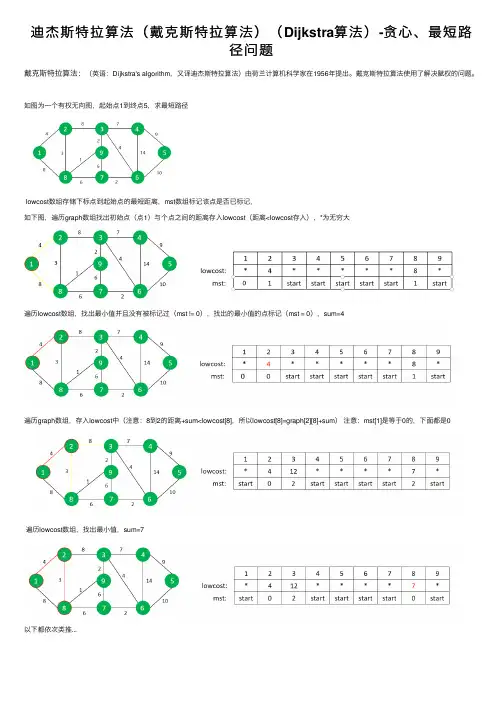
迪杰斯特拉算法（戴克斯特拉算法）（Dijkstra算法）-贪⼼、最短路径问题戴克斯特拉算法：（英语：Dijkstra's algorithm，⼜译迪杰斯特拉算法）由荷兰计算机科学家在1956年提出。

戴克斯特拉算法使⽤了解决赋权的问题。

如图为⼀个有权⽆向图，起始点1到终点5，求最短路径lowcost数组存储下标点到起始点的最短距离，mst数组标记该点是否已标记，如下图，遍历graph数组找出初始点（点1）与个点之间的距离存⼊lowcost（距离<lowcost存⼊），*为⽆穷⼤遍历lowcost数组，找出最⼩值并且没有被标记过（mst != 0），找出的最⼩值的点标记（mst = 0），sum=4遍历graph数组，存⼊lowcost中（注意：8到2的距离+sum<lowcost[8]，所以lowcost[8]=graph[2][8]+sum）注意：mst[1]是等于0的，下⾯都是0遍历lowcost数组，找出最⼩值，sum=7以下都依次类推...输⼊：9 14 1 5 1 2 41 8 82 8 32 3 88 9 18 7 63 9 29 7 63 4 73 6 47 6 24 6 144 5 96 5 10输出：24代码：#include <iostream>#include <bits/stdc++.h>using namespace std;#define MAX 100#define MAXCOST 0x7fffffff //int型最⼤值void prim(int graph[][MAX],int n,int start,int end){int lowcost[MAX];int mst[MAX];int sum=0;for(int i=1;i<=n;i++)//将与各点与起始点的距离存⼊lowcost中{lowcost[i]=graph[start][i];mst[i]=1;}mst[start]=0; //起始点被标记for(int i=1;i<=n;i++){if(mst[end]==0)//终点被标记结束{cout<<sum;break;}int min=MAXCOST;int minid=0;for(int j=1;j<=n;j++)//遍历lowcost数组，找最⼩值{if(lowcost[j]<min && mst[j]!=0){min=lowcost[j]; //最⼩值minid=j; //最⼩值下标}}//cout<<"V"<<mst[minid]<<"-V"<<minid<<"="<<min<<endl;sum=min;//cout<<sum<<endl;mst[minid]=0; //最⼩值下标点被标记for(int j=1;j<=n;j++)//找最⼩值点与各点的距离{if(graph[minid][j]==MAXCOST)//如果此点与最⼩值点没有联系（距离为最⼤值）则lowcost不变，跳过{continue;}else if(graph[minid][j]+sum<lowcost[j] && mst[j]!=0)//此点与最⼩点有联系，并且+sum<lowcost 并且此点没有被标记，则赋值给lowcost {lowcost[j]=graph[minid][j]+sum;}}}}int main(){int n,m;int start,end;int graph[MAX][MAX];cin>>n>>m>>start>>end;//初始化图Gfor(int i=1;i<=n;i++){for(int j=1;j<=n;j++){graph[i][j]=MAXCOST;}}//构建图Gfor(int k=1;k<=m;k++){int i,j,cost;cin>>i>>j>>cost;graph[i][j]=cost;graph[j][i]=cost;}prim(graph,n,start,end); return0;}。

dijkstra最短路径例题Dijkstra算法是一种用于解决加权有向图中单源最短路径的经典算法。

该算法通过迭代的方式逐渐确定源节点到其他所有节点的最短路径。

下面我们来看一个使用Dijkstra算法解决最短路径问题的例题。

假设有一个城市的公交站点图，其中包含A、B、C、D、E五个站点。

我们需要计算从起点站点A到终点站点E的最短路径，并输出最短路径上的所有中间站点。

给出的公交站点图如下：```A ----2---- B/ \ / \3 1 6 4/ \ / \D----3---- E----2---- C```上述图中，节点之间的数字代表了两个节点之间的距离。

根据Dijkstra算法的步骤，我们首先需要初始化起点A到所有其他节点的距离。

初始时，我们假设起点A到其它节点的距离均为无穷大，只有起点A到自身的距离为0。

同时，我们需要维护一个空的节点集合S，用于存放已经确定最短路径的节点，初始时S中没有任何节点。

接下来，我们需要在节点集合V中选择一个距离起点A最短的节点加入集合S，并更新其周边节点的距离值。

在这个例题中，起点A到节点B的距离为2，到节点D的距离为3，到节点E的距离为1，而到节点C的距离为无穷大。

因此，我们首先将节点E加入节点集合S，并更新节点B和节点D的距离值。

更新后的情况如下：```A ----2----B (2)/ \ / \3 1 6 4/ \ / \D----3---- E (0)----2---- C```然后，我们选取集合V中距离A最短的节点B加入集合S，并更新其周边节点的距离值。

根据上面的距离图，我们可以得到节点B到节点C的距离为6。

由于节点D和节点C的距离暂时无法确定，我们暂时将它们的距离设为无穷大。

更新后的情况如下：```A (0)----2----B (2)/ \ / \3 1 6 4/ \ / \D----3---- E (0)----2---- C (∞)```接下来，我们选取集合V中距离A最短的节点D加入集合S，并更新其周边节点的距离值。

题目：Dijkstra算法解决最短路径问题一、介绍Dijkstra算法Dijkstra算法是一种用于解决图中单源最短路径问题的经典算法。

它采用了贪心法的思想，即每次都选择当前最短的路径去更新相邻节点的距离，直到所有节点的最短路径都被更新为止。

Dijkstra算法的时间复杂度为O(V^2)，其中V表示图中节点的个数，因此适用于节点数较少的情况。

二、Dijkstra算法的基本步骤1. 初始化：将起始节点的距离设置为0，其他节点的距离设置为无穷大。

2. 确定当前最短距离节点：从未标记节点中选择距离最短的节点作为当前节点。

3. 更新相邻节点的距离：计算当前节点到相邻节点的距离，若小于原距离，则更新距离。

4. 标记当前节点：将当前节点标记为已访问。

5. 重复步骤2-4，直到所有节点都被标记为已访问或者没有可更新的节点。

三、经典例题：求解最短路径假设有一个带权有向图，节点表示城市，边表示城市之间的道路并标有权值，即两个城市之间的距离。

现要求从起始城市A到目标城市B的最短路径。

四、Java代码实现Dijkstra算法```javaimport java.util.Arrays;public class DijkstraAlgorithm {private static final int INF = Integer.MAX_VALUE; // 无穷大表示两节点不直接相连public int[] dijkstra(int[][] graph, int start) {int n = graph.length;int[] distance = new int[n]; // 存储起始节点到各节点的最短距离boolean[] visited = new boolean[n]; // 记录节点是否已被访问// 初始化distance数组Arrays.fill(distance, INF);distance[start] = 0;// 循环更新最短距离for (int i = 0; i < n - 1; i++) {int minIndex = findMinIndex(distance, visited); // 找到未被访问且距禃最短的节点visited[minIndex] = true;for (int j = 0; j < n; j++) {if (!visited[j] graph[minIndex][j] != INFdistance[minIndex] + graph[minIndex][j] < distance[j]) {distance[j] = distance[minIndex] +graph[minIndex][j];}}}return distance;}private int findMinIndex(int[] distance, boolean[] visited) { int minDist = INF, minIndex = -1;for (int i = 0; i < distance.length; i++) {if (!visited[i] distance[i] < minDist) {minDist = distance[i];minIndex = i;}}return minIndex;}public static void m本人n(String[] args) {int[][] graph = {{0, 6, 3, INF, INF},{INF, 0, INF, 1, INF},{INF, 2, 0, 1, 1},{INF, INF, INF, 0, 3},{INF, INF, INF, INF, 0}};DijkstraAlgorithm dijkstra = new DijkstraAlgorithm();int[] distance = dijkstra.dijkstra(graph, 0);for (int i = 0; i < distance.length; i++) {System.out.println("节点0到节点" + i + "的最短距禿：" + (distance[i] == INF ? "不可达" : distance[i]));}}}```五、代码解析1. 首先定义了一个常量INF表示无穷大，在实际应用中可以根据具体情况设置为合适的数值。