材料力学专项习题练习 弯曲应力
- 格式:doc
- 大小:1.52 MB
- 文档页数:21
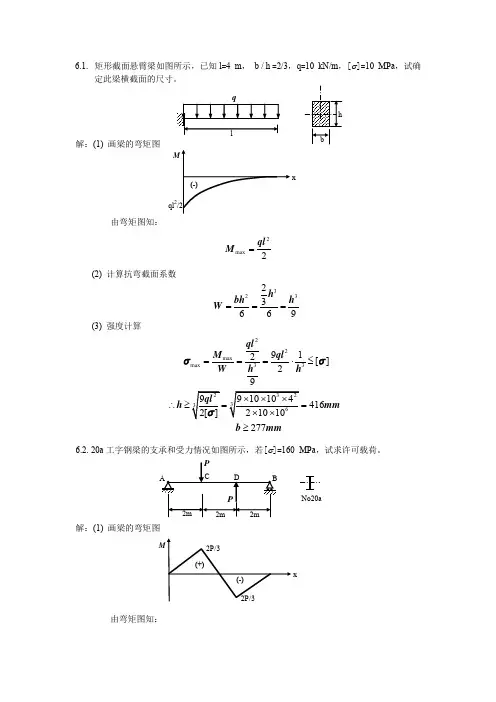
6.1. 矩形截面悬臂梁如图所示,已知l =4 m , b / h =2/3,q =10 kN/m ,[σ]=10 MPa ,试确定此梁横截面的尺寸。
解:(1) 画梁的弯矩图由弯矩图知:2max2ql M = (2) 计算抗弯截面系数32323669hbh h W === (3) 强度计算22maxmax 33912[]29416 277ql M ql h Wh h mm b mmσσ===⋅≤∴≥==≥ 6.2. 20a 工字钢梁的支承和受力情况如图所示,若[σ]=160 MPa ,试求许可载荷。
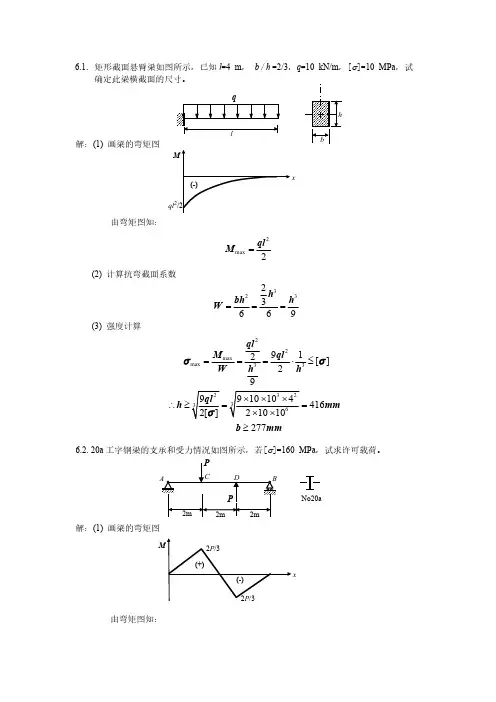
解:(1) 画梁的弯矩图由弯矩图知:No20a xql 2xmax 23P M =(2) 查表得抗弯截面系数6323710W m -=⨯(3) 强度计算max max 66223[]33[]3237101601056.8822PM P W W WW P kNσσσ-===⋅≤⨯⨯⨯⨯∴≤== 取许可载荷[]57P kN =6.3. 图示圆轴的外伸部分系空心轴。
试作轴弯矩图,并求轴内最大正应力。
解:(1) 画梁的弯矩图由弯矩图知:可能危险截面是C 和B 截面 (2) 计算危险截面上的最大正应力值C 截面:3max3332 1.341063.20.0632C C C C C M M MPa d W σππ⨯⨯====⨯ B 截面:3max3434440.91062.10.060.045(1)(1)32320.06B B B BB B B M M MPa D d W D σππ⨯====⨯-- (3) 轴内的最大正应力值MPa C 2.63max max ==σσx6.5. 把直径d =1 m 的钢丝绕在直径为2 m 的卷筒上,设E =200 GPa ,试计算钢丝中产生的最大正应力。
解:(1) 由钢丝的曲率半径知1M E M EI Iρρ=∴= (2) 钢丝中产生的最大正应力93max200100.510100 1MR ER MPa I σρ-⨯⨯⨯====6.8. 压板的尺寸和载荷如图所示。


弯曲应力练习题弯曲应力是工程力学中的重要概念,涉及到物体在受到弯曲力作用时的应力分布和变化。
掌握弯曲应力的计算方法对于力学领域的学习至关重要。
在本文中,我们将介绍一些常见的弯曲应力练习题,旨在帮助读者加深对弯曲应力的理解和运用。
1. 长方形截面材料的弯曲应力考虑一块长度为L、宽度为b、高度为h的长方形截面材料,在其最大弯曲力矩为M的作用下,我们希望计算其截面处的最大弯曲应力σ。
根据工程力学的理论,我们可以使用以下公式进行计算:σ = (M * y) / (I * c)其中,y表示距离截面中性轴的距离,I是截面的惯性矩,c是截面最大应力面的最大距离。
2. 悬臂梁的最大弯曲应力考虑一个长度为L、所受力矩为M的悬臂梁,我们希望计算其截面处的最大弯曲应力σ。
对于悬臂梁而言,最大弯曲应力出现在悬臂梁固定端。
根据工程力学的理论,我们可以使用以下公式进行计算:σ = (M * L) / (I * c)其中,M是所受力矩,L是悬臂梁的长度,I是截面的惯性矩,c是截面最大应力面的最大距离。
3. 圆柱体的弯曲应力考虑一个半径为r、所受力矩为M的圆柱体,我们希望计算其截面处的最大弯曲应力σ。
根据工程力学的理论,我们可以使用以下公式进行计算:σ = (M * r) / (I * c)其中,M是所受力矩,r是圆柱体的半径,I是截面的惯性矩,c是截面最大应力面的最大距离。
以上是三个常见的弯曲应力计算问题的解决方法。
在实际的工程应用中,我们需要根据具体情况选择合适的公式并进行计算。
同时,为了准确评估材料的弯曲性能,我们还需要了解材料的力学性质,如弹性模量、截面惯性矩等。
通过练习和实践,我们可以逐渐提高对弯曲应力问题的解决能力。
总结:本文简要介绍了弯曲应力的概念和计算方法,并提供了三个常见的弯曲应力练习题。
这些题目涉及到了不同结构的材料,如长方形截面材料、悬臂梁和圆柱体。
通过解决这些练习题,读者可以深入理解弯曲应力的计算过程,进一步掌握工程力学的基础知识。


第四章弯曲应力判断图弯矩的值等于梁截面一侧所有外力的代数和。
()负弯矩说明该截面弯矩值很小,在设计时可以忽略不计。
()简支梁上向下的集中力对任意横截面均产生负弯矩。
()横截面两侧所有外力对该截面形心力矩的代数和就是该截面的弯矩值。
()梁的任一横截面上的弯矩在数值上等于该截面任一侧所有外力对该截面形心的力矩代数和。
()在计算指定截面的剪力时,左段梁向下的荷载产生负剪力。
()在计算指定截面的剪力时,右段梁向下的荷载产生正剪力。
()梁纯弯曲时中性轴一定通过截面的形心。
()简支梁上受一集中力偶作用,当集中力偶在不改变转向的条件下,在梁上任意移动时,弯矩图发生变化,剪力图不发生变化。
()图示梁弯矩图的B点是二次抛物线的顶点。
()图示梁段上集中力偶作用点两侧的弯矩直线一定平行。
()(M图)下列三种斜梁A截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁B截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁C截面的弯矩均相同。
()l/2l/2l/2l/2l/2l/2梁弯曲时的内力有剪力和弯矩,剪力的方向总是和横截面相切,而弯矩的作用面总是垂直于横截面。
()一端(或两端)向支座外伸出的简支梁叫做外伸梁。
()##√悬臂梁的一端固定,另一端为自由端。
()##√弯矩的作用面与梁的横截面垂直,它们的大小及正负由截面一侧的外力确定。
()##√弯曲时剪力对细长梁的强度影响很小,所以在一般工程计算中可忽略。
()##√图示,外伸梁BC段受力F作用而发生弯曲变形,AB段无外力而不产生弯曲变形()##×由于弯矩是垂直于横截面的内力的合力偶矩,所以弯矩必然在横截面上形成正应力。
()##√抗弯截面系数是反映梁横截面抵抗弯曲变形的一个几何量,它的大小与梁的材料有关。
()##×无论梁的截面形状如何,只要截面面积相等,则抗弯截面系数就相等。
()##×梁弯曲变形时,弯矩最大的截面一定是危险截面。

4-1(4-1)试求图示各梁中指定截面上的剪力和弯矩。
解:(a)(b)(c)(d)=(e)(f)(g)(h)=返回4-2(4-2) 试写出下列各梁的剪力方程和弯矩方程,并作剪力图和弯矩图。
解:(a)(b)时时(c)时时(d)(e)时,时,(f)AB段:BC段:(g)AB段内:BC段内:(h)AB段内:BC段内:CD段内:返回4-3(4-3)试利用荷载集度、剪力和弯矩间的微分关系作下列各梁的剪力图和弯矩图。
返回4-4(4-4)试作下列具有中间铰的梁的剪力图和弯矩图。
返回4-5(4-6)已知简支梁的剪力图如图所示。
试作梁的弯矩图和荷载图。
已知梁上没有集中力偶作用。
返回4-6(4-7) 试根据图示简支梁的弯矩图作出梁的剪力图与荷载图。
返回4-7(4-15)试作图示刚架的剪力图、弯矩图和轴力图。
返回4-8(4-18)圆弧形曲杆受力如图所示。
已知曲杆轴线的半径为R,试写出任意横截面C上剪力、弯矩和轴力的表达式(表示成角的函数),并作曲杆的剪力图、弯矩图和轴力图。
解:(a)(b)返回4-9(4-19)图示吊车梁,吊车的每个轮子对梁的作用力都是F,试问:(1)吊车在什么位置时,梁内的弯矩最大?最大弯矩等于多少?(2)吊车在什么位置时,梁的支座反力最大?最大支反力和最大剪力各等于多少?解:梁的弯矩最大值发生在某一集中荷载作用处。
,得:当时,当M极大时:,则,故,故为梁内发生最大弯矩的截面故:=返回4-10(4-21)长度为250mm、截面尺寸为的薄钢尺,由于两端外力偶的作用而弯成中心角为的圆弧。
已知弹性模量。
试求钢尺横截面上的最大正应力。
解:由中性层的曲率公式及横截面上最大弯曲正应力公式得:由几何关系得:于是钢尺横截面上的最大正应力为:4-11(4-25) 矩形截面的悬臂梁受集中力和集中力偶作用,如图所示。
试求截面m-m和固定端截面n-n上A,B,C,D四点处的正应力。
解:对m-m及n-n截面,都给以坐标系如图所示。
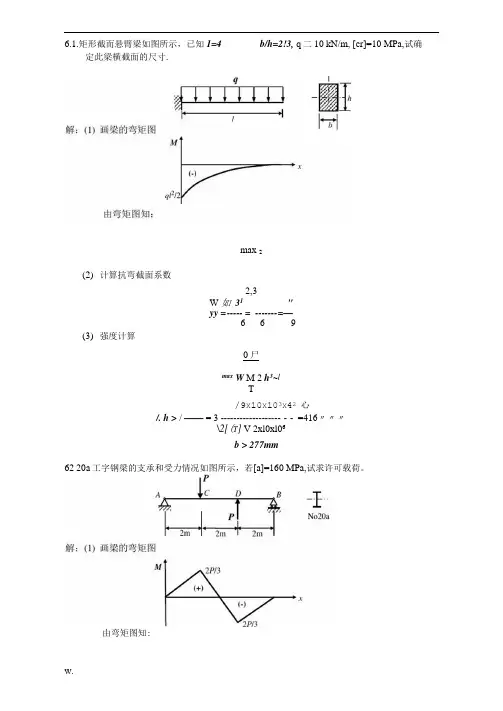
6.1.矩形截而悬臂梁如图所示,已知1=4 b/h=2!3, q二10 kN/m, [cr]=10 MPa,试确定此梁横截面的尺寸.max 2(2)计算抗弯截面系数2,3W 如31"yy = ----- = ------- =—6 6 9(3)强度计算0尸max W M 2 h3~[T/9X10X103X42心/. h > / —— = 3 ------------------- - - =416〃〃〃\2[(T] V 2xl0xl06b > 277mm62 20a工字钢梁的支承和受力情况如图所示,若[a]=160 MPa,试求许可载荷。
由弯矩图知:2P= = J_.pgEW W 3W.• A 哄=3x237xl0F60>d。
”= %.8 球2取许可载荷[P] = 57AN解:(1)画梁的弯矩图M c M c 32xl.34xl03=—=—Y = :— = 63.2MPaW c诚;. n x 0.06?"3TB截面:0.9xlO3 5z 4——;------------ -- = 62.1 MPa力以八d;、〃x0.06 〃 0.045、---- U ——r)------------ (1 —----- r-)32 矶32 0.064(3)轴内的最大正应力值(2)查表得抗弯截面系数(3)强度计算2P、=——W =237x10^7/1maxbfmax63.图示圆轴的外伸部分系空心轴.试作轴弯矩图,并求轴内最大正应力.由弯矩图知:可能危险截面是C和B截而(2)计算危险截而上的最大正应力值C截面:解:(1)画梁的弯矩图M t = 308M H(2)计算抗弯截面系数(3)强度计算 许用应力[(r] = ^- = — = 253MPa n 1.5强度校核308 inA1/rn r 】b” = —- = ------------------ I T = 1961"“ Y b maxW 1.568x1 Of压板强度足够。

弯曲内力和应力基本概念练习下卷材料力学 - 1 - 弯曲内力练习一、选择题1.外伸梁受均布载荷作用,如图所示。
以下结论中()是错误的。
A.AB段剪力表达式为FQ(x)=-qx;B.AB段弯矩表达式为M(x)=-1qx2; 2C.BCqa2段剪力表达式为FQ(x)=2L2;(L-x)。
D.BC段弯矩表达式为M(x)=-qa2L题1图题2图2.外伸梁受集中力偶作用,如图所示,以下结论中()是错误的。
A.当力偶作用点C位于支座B的右侧时,梁的弯矩图为梯形;B.当C点位于支座B的右侧时,梁上各截面的弯矩M(x)≥0;C.当C点在梁上移动时,梁的剪力图不改变;D.当C点在梁上移动时,梁的中央截面上弯矩不改变。
第 1 页共 6 页题3图下卷材料力学 - 2 -3.简支梁受集中力作用,如图所示,以下结论中()是错误的。
A.AC段,剪力表达式为 FS(x)=Fb; LFbx;B.AC段,弯矩表达式为M(x)=LC.CB段,剪力表达式为 FS(x)=Fa; LFa(L-x)。
D.CB段,弯矩表达式为M(x)=L4.简支梁的四种受载情况如图,设M1、M2、M3、M4分别表示梁(a)、(b)、(c)、(d)中的最大弯矩,则下列结论中()是正确的。
A.M1 >M2 = M3 >M4;B. M1 >M2 > M3 >M4;C.M1 >M2 >M3 = M4;D. M1 >M2 >M4> M3 。
(a)(b)(c)(d)5.外伸梁受均布载荷作用,如图所示。
以下梁的剪力、弯矩图第 2 页共 6 页下卷材料力学 - 3 - 中()是正确的。
A.(a);B.(b);C.(c);D.(d)。
F sFs弯曲应力一. 选择题1.在推导弯曲正应力公式σ=My时,假设纵向线段间无挤压,IZ 这是为了()。
A.保证正应力合力FN = ∫A σdA=0;B.保证纵向线段为单向拉伸(压缩);C.保证梁发生平面弯曲;D.保证梁不发生扭转变形。

弯曲应力习题答案在材料力学中,弯曲应力是结构分析中的一个重要概念,它涉及到梁或板在受到弯曲作用时内部产生的应力。
以下是一些弯曲应力习题的答案示例:习题一:简单梁的弯曲应力计算问题描述:一根长为 \( L \) 米,截面为矩形的梁,宽 \( b \) 米,高 \( h \) 米,材质为钢,弹性模量 \( E \) 为 \( 200 \) GPa。
梁的一端固定,另一端自由,中间受到一个集中力 \( P \) 的作用。
解答:1. 首先,确定梁的截面惯性矩 \( I \):\[ I = \frac{b \cdot h^3}{12} \]2. 根据梁的受力情况,计算梁的弯曲应力 \( \sigma \):\[ \sigma = \frac{M \cdot c}{I} \]其中 \( M \) 是弯矩,对于集中力 \( P \) 作用在梁的中点,弯矩 \( M \) 为 \( \frac{PL}{4} \)。
3. 将弯矩代入弯曲应力公式中:\[ \sigma = \frac{P \cdot L \cdot c}{4 \cdot I} \] 其中 \( c \) 是梁截面上距离中性轴的距离,对于矩形截面,\( c = \frac{h}{2} \)。
4. 将已知数值代入公式,计算出弯曲应力。
习题二:悬臂梁的弯曲应力分析问题描述:一根悬臂梁,长度 \( L \) 米,材料的弹性模量 \( E \) 为 \( 200 \) GPa,梁的一端固定,另一端受到一个向下的集中力 \( P \)。
解答:1. 悬臂梁在末端受到集中力作用时,最大弯矩 \( M \) 出现在梁的末端,其值为 \( P \cdot L \)。
2. 假设梁的截面为圆形,半径 \( r \),则截面惯性矩 \( I \) 为: \[ I = \frac{\pi r^4}{4} \]3. 计算弯曲应力 \( \sigma \):\[ \sigma = \frac{M}{I} = \frac{P \cdot L}{\frac{\pir^4}{4}} \]4. 将已知数值代入公式,计算出弯曲应力。
弯曲应力1. 圆形截面简支梁A,B 套成,层间不计摩擦,材料的弹性模量E 严2E A 。
求在外力偶矩A/。
作用下,A,3中最大正应力的比值也有4个答案: (心;O(c)r 答:B2. 矩形截面纯弯梁,材料的抗 拉弹性模量耳大于材料的抗压 弹性模量瓦,则正应力在截面 上的分布图有以下4种答案:答:C3. 将厚度为2 mm 的钢板尺与一曲面密实接触,已 知测得钢尺点A 处的应变为-岛,则该曲面在点A 处的曲率半径为 ___________ mm ° 答:999 mm4. 边长为"的正方形截面梁,按图示两种不同形式放置,在相同弯矩作用下,两者最大正应力之比竺4= ________(bnux)b5•—工字截面梁,截面尺寸如图,h = b 」= 15。
的弯矩约为截面上总弯矩的88%o•工 My “ 2M 严彳 “t M/ 证: b = -j —, = —j — x J y( y^dy) = 1 820 x其中:积分限B = t + - , A = - 为翼缘弯矩2 26.直径d = 20 mm 的圆截面钢梁受力如图,已知弹性模量 E = 200 GPa , d = 200mm ,欲将其中段A3弯成 ° = 12 m 的圆弧,试求所需载荷,并计算最大弯曲北应力。
7. 钢筋横截面积为密度为° ,放在刚性平面上,一端加力提起钢筋离F2//3厂P(B)r试证明,此梁上,下翼缘承担 解:14而—第57页Ah/2h/2B开地面长度丄。
试问F应多大?3解:截面C曲率为零8.矩形截面钢条长/,总重为F,放在刚性水平面上,在钢条A端作用乂向上3 的拉力时,试求钢条内最大正应力。
解:在截面C处,有丄=^=0p EIAC段可视为受均布载荷§作用的简支梁9.图示组合梁山正方形的铝管和正方形钢杆套成,在两端用刚性平板牢固联接。
已知:钢和铝的弹性模量关系为£s=3£a;在纯弯曲时,应力在比例极限内。
弯曲应力小结一、常用公式 (1)惯性矩公式(2)弯曲正应力公式(3)正应力强度校核(4)形心计算公式11ni cic niA yy A=∑∑(5)平行轴公式22,y yc z zc I I a A I I b A =+=+I b h Z =312,W b h Z =26I d Z =π464,W d Z =π332σ=M y I zmaxmax []ZM W σσ=≤二、补充习题1、受均布载荷作用的简支梁如图所示,试求: (1)1—1截面上1、2两点的正应力; (2)此截面上的最大正应力; (3)全梁的最大正应力;160M kNm =,545.83210z I m -=⨯,436.4810z W m -=⨯,1261.7MPa σσ==1max 92.6MPa σ=,max 104.2MPa σ=2、受纯弯曲的空心圆截面梁如图所示。
已知:弯矩M= l kN.m ,外径D=50mm ,内径d=25mm 。
试求横截面上a 、b 、c 及d 四点的应力。
74I 2.8810m z -=⨯,86.8MPa()a σ=压应力,43.4MPa()b σ=拉应力75.3MPa()c σ=压应力,0d σ=3、已知槽形截面梁弯矩如图所示,试求梁横截面上的最大拉应力。
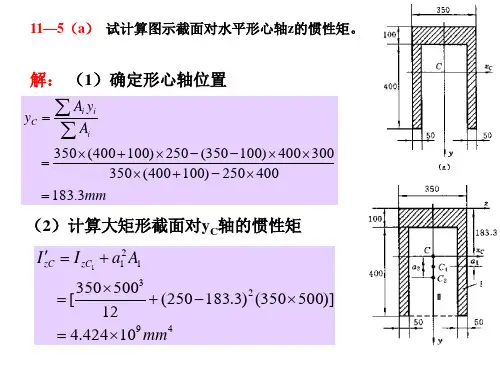
(1)求形心mm 317mm 400250500350200400250250500350=⨯-⨯⨯⨯-⨯⨯=y过形心C 取z 轴,截面对z 轴的惯性矩为23z )250317(500350500350121{I -⨯⨯+⨯⨯=423mm ]})200317(300250400250121[-⨯⨯+⨯⨯- 46mm 101728⨯=B 截面的最大拉应力为MPa 06.1Pa )10(10172810)317500(101043633max =⨯⨯⨯-⨯⨯==--y I M σz B BtC 截面的最大拉应力为MPa 38.1Pa )10(10172810317105.743633max =⨯⨯⨯⨯⨯==--y I M σz C Ct可见,梁的最大拉应力发生在C 截面的下部边缘线上。
注:由于本书没有标准答案,这些都是我和同学一起做的答案,其中可能会存在一些错误,仅供参考。
习 题6-1厚度mm h 5.1=的钢带,卷成直径 D=3m 的圆环,若钢带的弹性模量E=210GPa ,试求钢带横截面上的最大正应力。
解: 根据弯曲正应力公式的推导: Dy E yE 2..==ρσ MPa D h E 1053105.110210.39max=⨯⨯⨯==-σ6—2直径为d 的钢丝,弹性模量为E ,现将它弯曲成直径为D 的圆弧。
试求钢丝中的最大应力与d /D 的关系。
并分析钢丝绳为何要用许多高强度的细钢丝组成。
解: ρσyE .= Dd E ED d .22max ==σ max σ与Dd成正比,钢丝绳易存放,而引起的最大引力很小.6—3 截面形状及尺寸完全相同的一根钢梁和一根木梁,如果所受的外力也相同,则内力是否相同?横截面上正应力的变化规律是否相同?对应点处的正应力与纵向线应变是否相同? 解: 面上的内力相同,正应力变化规律相同。
处的正应力相同,线应变不同6—4 图示截面各梁在外载作用下发生平面弯曲,试画出横截面上正应力沿高度的分布图.6—5 一矩形截面梁如图所示,已知F=1.5kN 。
试求(1) I —I 截面上A 、B 、C 、D 各点处的正应力; (2) 梁上的最大正应力,并指明其位置。
解:(1)m N F M .3002.0*10*5.12.0*3===MPa M I y M z A 11110*30*1812*10*15*.1233===--σ A B σσ-= 0=C σMPa M D 1.7410*30*1812*10*)5.15(*1233==--σ MPa W Fl z 5.16610*30*186*10*300*10*5.19233max ===--σ 位置在:固定端截面上下边缘处。
6—6 图示矩形截面简支梁,受均布载荷作用。
已知载荷集度q=20kN /m ,跨长l =3,截面高度=h 24cm ,宽度=b 8cm 。