当前位置：文档之家 › 材料力学弯矩曲率关系推导

材料力学弯矩曲率关系推导

  • 格式：docx
  • 大小：37.29 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

材料力学第5章 弯曲位移分析

材料力学第5章 弯曲位移分析
§5-1 基本概念及工程实例 §5-2 挠曲线的微分方程 §5-3 用积分法求弯曲位移 §5-4 用叠加法求弯曲位移 §5-5 提高弯曲刚度的措施
§5-1 基本概念及工程实例
一、为什么要研究弯曲变形
M [ ] 仅保证构件不会发生破坏，
Wz 但如果构件的变形太大也不能正常工作。 1、构件的变形限制在允许的范围内。
例题2求图所示悬臂梁B端的挠度与转角。 M x 1 qL x2
B
2
A
x
l
x
EIz
Mx
1 2
q
L
x
2
y
边界条件
EIz
EIz
1 6
qL
x3
C1
EIz
1 24
qL
x4
C1 x
C2
x0 0
x0 0
xL
B
qL3 6EIz
qL3 C1 6EIz
C2
qL3 24EIz
B
qL4 8EIz
q L x3 L3 6EIz
o
xo
x
M
M

d2y dx2 0
y
M
M
d2y dx 2
0
y
因此, w与 M 的正负号相反
d 2ω
dx 2
1
(
dω dx
)2
3
M(x) EI Z
w2与 1 相比十分微小而可以忽略不计,故上式可近似为
d 2ω M(x)
dx 2
EI Z
此式称为 梁的挠曲线近似微分方程
近似原因 : （1） 略去了剪力的影响; （2） 略去了 w2项;
q L x4 4L3 x L4 24 EI z

弯矩 曲率关系

弯矩 曲率关系

c0 0.00,2cu0.0033
11.0
1
0.8, 0.7,
fcu 50Mpa fcu 50Mpa
线性插值（《混凝土结构设计
规范》GB50010 ）
六、受弯构件正截面简化分析
1. 压区混凝土等效矩形应力图形（极限状态下）
定义：
x h0
xn=nh
0
1c0
yc C
x=1xn
对试验梁，已知b、h0、As、fc、fy、Es， Mu
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
sAs
s= fyAs
y
fyAs s>y
四、受弯构件的试验研究
2. 试验结果
结论
•适筋梁具有较好的变形能力，超筋梁和少筋梁的破坏具有突然性，设计 时应予避免
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢筋屈服的同 时，混凝土压碎
二、骨架曲线的弯矩-曲率关系
1. 基本假定
P
平截面假定----平均应变意义上
As’
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
as b
s
b c
(1-n)h0
忽略剪切变形对梁、柱构件变形的影响
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的相容关系
as h/2as h h/2as
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
As
as 1
h/2-

材料力学(理工科课件)第六章 弯曲变形)

材料力学(理工科课件)第六章 弯曲变形)

§6-1 基本概念及工程实例 （Basic concepts and example problems）
一、工程实例（Example problem）
(Deflection of Beams)
但在另外一些情况下,有时却要求构件具有较大的弹性变 形,以满足特定的工作需要.
例如,车辆上的板弹簧,要求有足够大的变形,以缓解车辆受
M 0 w 0
x
O
M 0 w 0
M
(Deflection of Beams)
w (1 w )
2 3 2

M ( x) EI
2 w 与 1 相比十分微小而可以忽略不计,故上式可近似为
w"
M ( x) EI
(6.5)
此式称为 梁的挠曲线近似微分方程（differential equation of the deflection curve） 近似原因 : （1） 略去了剪力的影响; （2） 略去了 w2项; （3） tan w w( x )
x Cx D
4
(Deflection of Beams)
边界条件x=0 和 x=l时, w 0
梁的转角方程和挠曲线方程 A 分别为 q 2 3 3 (6lx 4 x l ) 24 EI qx 2 3 3 w (2lx x l ) 24 EI 最大转角和最大挠度分别为 在 x=0 和 x=l 处转角的绝对值相等且都是最大值，
A a l D B
b
(Deflection of Beams)
解: 梁的两个支反力为
FRA F FRB F b l a l
x
l x
F FRA
A 1 a D b 2

《弯矩曲率关系》课件

《弯矩曲率关系》课件

曲率的定义
曲率：描述曲线弯曲程度的量， 定义为曲线上任一点处切线方向 角的变化量与经过的弧长的比值
。
在数学上，曲率是用来衡量曲线 上某一点附近的小弧段弯曲程度
的量。
对于直线，其曲率为0；对于圆 ，其曲率是一个常数，等于圆的
半径倒数。
曲率的计算
曲率计算公式：K = lim(Δs->0) [Δs / (Δt)^2] / lim(Δt>0) [Δs / Δt]
在机械工程中的应用
传动系统设计
在机械传动系统中，弯矩曲率关系对于齿轮、轴等部件的设计和优化具有指导意义。了解弯矩与曲率的关系有助 于提高传动系统的效率和稳定性。
疲劳分析
在机械部件的疲劳分析中，弯矩曲率关系是评估其疲劳寿命的重要因素之一。通过对弯矩和曲率的变化规律进行 分析，可以预测部件的疲劳寿命和潜在的疲劳断裂风险。
在工程结构中，弯矩和曲率是密切相关的。例如，在桥梁、建筑和机械设计中，需 要考虑到结构的弯曲程度和弯矩之间的关系。
当结构受到外力作用时，会发生弯曲变形，曲率会发生变化，同时弯矩也会随之改 变。因此，在设计时需要考虑到结构的承载能力和稳定性。
了解弯矩与曲率的关系有助于工程师更好地设计结构，确保其安全性和稳定性。
需要研究弯矩曲率关系在不同温度、湿度等环境 条件下的变化规律。
需要探索弯矩曲率关系在复合材料、智能材料等 新型材料中的应用。
对学习者的建议
学习者应该深入理解弯矩和曲 率的定义及测量方法。
学习者应该掌握弹性力学和 材料力学的基本原理，以便 更好地理解弯矩曲率关系。
学习者可以通过实验和实践来 加深对弯矩曲率关系的理解和
应用。THANΒιβλιοθήκη S感谢观看详细描述
弯矩是材料力学中一个重要的概念，用于描述弯曲变形过程 中截面所受到的力矩作用。在材料受到弯曲时，截面上会产 生剪力和弯矩，弯矩的大小与剪力和中性轴距离有关。

材料力学

材料力学

bh3 bh2 12 h 6 2
h
y
z
实心圆
空心圆
z y
z C y d
D
Iz
D 4
64
Iz
D 4 d 4
64 64
4
Wz
D 3
32
d Wz (1 ) D 32
D 3
41
箱形截面
y
Iz Wz ymax
BH bh 12 12 H 2
3 3
x y
y
y
min
xy
x
2 一点处有三个主应力，按代数 值大小排列分别记为 1，2， 3
2 0、（2 0 ） 0、（ 0 ）
x
max
1 2 3
极值剪应力
x y 2 2 max max min ( ) xy 2 2 min
P P P d Pbs t
挤压面
有效挤压面积 dt
双剪——有两个剪切面
Q=P/2
Q
P/2 P P P P/2 二个剪切面 P
Q
三、实用计算及强度条件
实用计算
1、假定剪切面上的应力分布规律；
2、确定破坏应力的试验，所用试件的形状及受力 情况与实际构件相似或相同。
强度条件 剪切强度条件 剪断条件
m=Q/Am [m]
1 2
max
1 3
2
3
2 1
12
2 2 3 23 2 1 3 13 2
五、 复杂应力状态下应力应变关系
1 x x y E
1 y y x E
y

材料力学5-弯曲强度

材料力学5-弯曲强度

1. 杆件轴向拉伸或压缩时的变形
载荷与内力成正比，因此荷载与它所引起的变形成 线性关系：载荷增加一倍，变形增加一倍。
2. 圆轴扭转时的变形
载荷与内力成正比，因此荷载与它所引起的变形成 线性关系：载荷增加一倍，变形增加一倍。
3. 梁的弯曲变形
载荷它所引起的变形成线性关系：载荷增加一倍， 变形增加一倍。 那么，如果变形中有同载荷无关的项，意味着载荷 为0时，梁也有变形。
2.曲率与弯矩的符号关系 M与w''的符号相反。 梁弯曲时轴线曲率：
7.2 用积分法求梁的位移
梁的挠曲线近似微分方程:
式中积分常数C、D由约束条件和连续条件（统称 边界条件）确定。
要求： （1）约束处满足位移约束条件； （2）梁轴中间的点满足连续与光滑条件弯矩方程不连 续时要分段积分。
注意
1. 分段连续弯矩方程必须从原点沿x的正向依 次写出； 2. 对含（x-a）项可不展开，把它视为新变量 积分，更为方便； 3. 挠曲轴是一条连续而光滑的曲线（中间铰链 除外，该处只连续而不光滑）,为此必须满 足连续光滑条件。
7.3 用叠加法计算梁的变形 在材料服从胡克定律（线弹性）、且变形很小（小 变形）的前提下，载荷与它所引起的变形成线性关 系。
弯曲变形的基本概念 1.挠曲线
挠曲线方程：
2.挠度和转角 挠度w：横截面 形心处的铅垂位 移。
ห้องสมุดไป่ตู้
转角θ：横截面绕 中性轴转过的角 度。 规定向y正向的挠 度为正，顺针向 的转角为正。 转角方程
曲线y = f ( x )的曲率为：
几何方法
材料力学方法
又因为挠曲线非常平坦，即w’<<1
第 七 章 梁的位移

材料力学弯曲变形

材料力学弯曲变形

第18页/共34页
三、提高梁的刚度的措 施 由梁在简单荷载作用下的变形表和前面的变形计算可看：
梁的挠度和转角除了与梁的支座和荷载有关外还取决于 下面三个因素：
材料——梁的位移与材料的弹性模量 E 成反比； 截面——梁的位移与截面的惯性矩 I 成反比； 跨长——梁的位移与跨长 L 的 n 次幂成正比。
1 3
(L2
b2 )
e) 跨中点挠度及两端端截面的转角
y
x=
L 2
=
Fb 48EI
(3L2
4b2 );
=
y
x=
L 2
=
Fb 24LEI
L2 4b2
两端支座处的转角——
A
=
Fab(L 6LEI
b)
;
B
=
Fab(L 6LEI
a)
第8页/共34页
讨论：1、此梁的最大挠度和最大转角。
左 侧
1max y1 = 0 x1 = 0
等于各载荷单独作用下的弯矩的代数和。
M = M1 M2 M3 EIyi = M i (x)
EIy1 = M1( x) EIy2 = M 2 ( x) EIy3 = M 3 ( x)
第12页/共34页
叠加法计算梁的变形
EIy = M (x)
y = y1 y2 y3 M (x) = M1 M 2 M3
第5页/共34页
例：求图示悬臂梁自由端的挠度及转角( EI=常数）。
解：a) 建立坐标系并写出弯矩方程
M (x) = F(L x)
b) 写出微分方程并积分
EIy = M (x) = F(L x)
EIy
=
1 2
F
(L

弯矩曲率关系

弯矩曲率关系

1. 基本假定
混凝土受压时的应力-应 变关系
n

2

1 60
(
fcu

50),当n

2时，取n

2
当应力较小时，如 c 0.3 fc时，可取 c Ecc
c fc
c

f
c

1

1


c 0
n


o
0
0 0.002 0.5 fcu 50105
四、受弯构件的试验研究
2. 试验结果
最小配筋率
四、受弯构件的试验研究
2. 试验结果 P
M
超筋 平衡
III
适筋
L/3 L
II 少筋 I O
最小配筋率
c
c
c
c
L/3
(c’<u) c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
As
as
h/2as h h/2as
as
1
i

Zi

截面中心线 s n
As
b
c1 s ci M
N
X 0,
n
ci Ai


' s
As'
s As

N

0
i 1
sAs ci
sAs
M 0,
荷载分 配梁 P

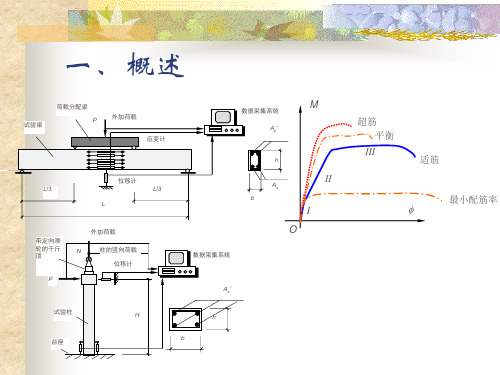
第二章弯矩曲率关系

第二章弯矩曲率关系
X 0,
n

i 1
ci
Ai s' As' s As N 0
n
2） 假定和 值
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )＝0 2 2
3） 由相容方程求出各条带混凝土的应变及钢筋的应变； 4） 由物理关系求出相应的应力，拉区混凝土条带的应变 超过其极限受拉应变时，应对其进行处理；
2） 假定 值
X 0,
n

i 1
ci
Ai s' As' s As N 0
n
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )＝0 2 2
3） 由相容方程求出各条带混凝土的应变及钢筋的应变； 4） 由物理关系求出相应的应力，拉区混凝土条带的应变 超过其极限受拉应变时，应对其进行处理；
5） 将各应力值代入第一平衡方程，判断是否满足平衡条件： 如不满足，需要调整 值直至满足为止，如满足平衡条件， 则由第二平衡方程求出M，然后重复步骤1～5
6） 当符合破坏条件时，停止计算。
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
M - 关系的计算方法之二 ：分级加荷载法
1） 取M＝M＋M
h h/2as
as b
n
As
对钢筋混凝土柱， 有时也可能会出现 s < 0
s s ( s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
as h/2as h h/2as as b 1 i Zi 截面中心线 n As As

材料力学知识点

材料力学知识点

第六章弯曲变形知识要点1、弯曲变形的概念1）、挠曲线弯曲变形后梁的轴线变为挠曲线。

平面弯曲时，挠曲线为外力作用平面内的平面曲线。

2）、平面弯曲时的变形在小变形情况下，梁的任意二横截面绕各自的中性轴作相对转动，杆件的轴线变为平面曲线，其变形程度以挠曲线的曲率来度量。

1》纯弯曲时，弯矩—曲率的关系（由上式看出，若弯曲刚度EI为常数则曲率为常数，即挠曲线为圆弧线）2》横力弯曲时，弯矩—曲率的关系3）、平面弯曲时的位移1》挠度——横截面形心在垂直于梁轴线方向上的线位移，以表示。

2》转角——横截面绕其中性轴旋转的角位移，以表示。

挠度和转角的正负号由所选坐标系的正方向来确定。

沿y轴正方向的挠度为正。

转角的正负号判定规则为，将x轴绕原点旋转90°而与y轴重合，若转角与它的转向相同，则为正，反之为负。

4）、挠曲线近似微分方程5）、受弯曲构件的刚度条件，2、积分法求梁的挠度和转角由积分常数C、D由边界条件和连续性条件确定。

对于梁上有突变载荷（集中力、集中力偶、间断性分布力）的情况，梁的弯矩M(x)不是光滑连续函数，应用上式时，应分段积分，每分一段就多出现两个积分常数。

因此除了用边界条件外，还要用连续性条件确定所有的积分常数。

边界条件：支座对梁的位移（挠度和转角）的约束条件。

连续条件：挠曲线的光滑连续条件。

悬臂梁边界条件：固定端挠度为0，转角为0连续条件：在载荷分界处（控制截面处）左右两边挠度相等，转角相等简支梁边界条件：固定绞支座或滑动绞支座处挠度为0连续条件：在载荷分界处（控制截面处）左右两边挠度相等，转角相等连接铰链处，左右两端挠度相等，转角不等3、叠加原理求梁的挠度和转角1）、叠加原理各载荷同时作用下梁任一截面的挠度和转角等于各个载荷单独作用时同一截面挠度和转角的代数和。

2）、叠加原理的限制叠加原理要求梁某个截面的挠度和转角与该截面的弯矩成线性关系，因此要求：1》弯矩M和曲率成线性关系，这就要求材料是线弹性材料2》曲率与挠度成线性关系，这就要求梁变形为小变形4、弯曲时的超静定问题——超静定梁1）、超静定梁约束反力数目多于可应用的独立的静力平衡方程数的梁称为超静定梁，它的未知力不能用静力平衡方程完全确定，必须由变形相容条件和力与变形间的物理关系建立补充方程，然后联立静力平衡方程与补充方程，求解所有的未知数。

材料力学-弯曲变形(三者关系)

材料力学-弯曲变形(三者关系)

dFS ( x) q ( x) dx
dM ( x) FS ( x)dx
b M a dM ( x) a FS ( x)dx
Mb
dFS ( x) q( x)dx

FSb FSa
b dFS ( x) a q( x)dx
b M b M a a FS ( x)dx
b FSb FS a a q( x)dx
斜直线 M M M 图 M x x 特 征 5 增函数 降函数
降函数 增函数 曲线
M x x
FS2
FS1–FS2=F
有转折
M x
向上突变
M
M2 M1 x
机械基础-材料力学-弯曲变形
2013-2-4 M 2 M1M e
载荷集度、剪力和弯矩间的关系 4、将微分关系转为积分关系
dM ( x) FS ( x) dx
1
2013-2-4
1.25
– qa2
3 2 qa 2 机械基础-材料力学-弯曲变形
M B qa2
qa2 M C M B 2 3qa2 2
2013-2-4
8
用简易作图法画下列各图示梁的内力图。 Me=qa2 FA FD 解：求支反力 q
A B C D
载荷集度、剪力和弯矩间的关系
qa qa FA ; FD 2 2
4
机械基础-材料力学-弯曲变形
2013-2-4
二、剪力、弯矩与外力间的关系
载荷集度、剪力和弯矩间的关系
外 力
无外力段
q=0 水平直线 FS FS
均布载荷段
q<0 q>0
集中力
F
C
集中力偶
Me C

材料力学第7章

材料力学第7章

积分一次： Fb 2 EIw1 x C1 2l 积分二次： Fb 3 EIw1 x C1 x D1 6l
11
CB段（a x l）: 弯矩方程：
Fb M 2 x x F x a l
挠曲线近似微分方程：
Fb EIw2 x F x a l Fb 2 F 2 x x a C2 积分一次： EIw2 2l 2
ቤተ መጻሕፍቲ ባይዱ 1 x 0
Fab l b , B 2 6lEI
Fab l a B = 6lEI
Fl 3 Fl 3 Fl 3 2 EI 6 EI 3EI
7
wmax w x l
例题7.2：图示弯曲刚度为EI的简支梁，受集度为q的均布 荷载作用，试求梁的挠曲线方程和转角方程，并确定其最 大挠度和最大转角。 解：由平衡方程得支座反力 ql FA FB 2 建立坐标系，得梁的弯矩方程为 1 1 2 M x qlx qx 2 2 梁挠曲线近似微分方程
1 3 C ql ， D 0 24
9
梁的转角方程
q w (4 x3 6lx 2 l 3 ) 24 EI
梁的挠曲线方程
(5)
qx w ( x3 2lx 2 l 3 ) 24 EI
最大转角
(6)
max
ql 3 A B 24 EI
2
最大挠度
M ( x) F l x
1
挠曲线近似微分方程
EIw M x F l x 2 两次积分，得 1 2 EIw Flx Fx C 2 1 1 3 2 EIw Flx Fx Cx D 2 6

简支梁弯矩推导

简支梁弯矩推导

简支梁弯矩公式推导过程为：M=FL/4，其中M代表弯矩，F代表作用在梁上的力，L代表梁的长度。

这个公式适用于只有一个集中力作用在梁上的情况。

如果有其他载荷作用在梁上，需要将它们拆分成若干个集中力，并分别计算它们产生的弯矩，最后将它们相加得到总的弯矩。

此外，如果梁的截面发生变化或者梁的材料发生变化，还需要考虑截面形状和材料属性对计算结果的影响。

简支梁的弯矩计算公式是力学中的基础知识，它可以用于求解各种工程问题。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

材料力学弯矩曲率关系推导
一、概述
在材料力学中，弯矩曲率关系是非常重要的一个概念。

它描述了杆件在受到弯曲作用时的变形情况，是理解和分析结构力学问题的基础。

本文将从基本概念入手，介绍弯矩曲率关系的推导过程，并给出实际应用案例。

二、基本概念
1. 弯矩
弯矩是指杆件在受到弯曲作用时所产生的内力。

通常用M表示，单位为牛米（N·m）。

2. 曲率
曲率是指杆件在受到弯曲作用时所产生的变形程度。

通常用ρ表示，单位为米（m）。

3. 弯矩曲率关系
弯矩和曲率之间存在着一定的关系，称为弯矩曲率关系。

它描述了当
外力作用于杆件上时，杆件内部所产生的应力和变形情况。

三、推导过程
1. 假设条件
为了方便推导，我们假设杆件为梁形截面，并且只受到纵向载荷和垂
直于截面平面方向的剪力和弯矩作用。

2. 基本方程
根据材料力学的基本原理，我们可以得到以下方程：
σ = M·y/I
其中，σ表示截面内的应力，M表示弯矩，y表示距离中性轴的距离，I表示截面惯性矩。

3. 推导过程
为了推导出弯矩曲率关系，我们需要对上述方程进行求导。

具体过程如下：
dσ/dy = M/I
d^2σ/dy^2 = d(M/I)/dy = -M/ I^2 · dI/dy
其中，dσ/dy表示应力沿截面高度方向的变化率（即曲率），
d^2σ/dy^2表示曲率沿截面高度方向的变化率（即弯矩曲率关系）。

由于I是与截面形状和尺寸有关的常数，在计算时可以视为已知量。

因此，我们可以将上式改写为：
d^2σ/dy^2 = -M/ I^2 · dI/dx
这就是弯矩曲率关系的基本公式。

它表明了当外力作用于杆件上时，杆件内部所产生的应力和变形情况之间存在着一定的联系。

四、实际应用
1. 弯曲分析
利用弯矩曲率关系，我们可以对杆件的弯曲情况进行分析。

通过计算杆件所受的弯矩和曲率，可以得出杆件内部应力和变形情况，从而判
断其是否满足设计要求。

2. 结构设计
在结构设计中，弯矩曲率关系也是一个非常重要的概念。

通过对结构中各个部分所受的载荷进行分析，并根据弯矩曲率关系计算出所需的截面形状和尺寸，可以保证结构的安全性和稳定性。

3. 工程实践
弯矩曲率关系在工程实践中也有广泛的应用。

例如，在建筑工程中，工程师需要对楼板、梁、柱等各个部分进行弯曲分析，并根据实际情况确定其截面形状和尺寸；在机械制造领域中，工程师需要对各种零件进行弯曲分析，并根据实际情况确定其材料选择和加工工艺。

五、总结
本文介绍了弯矩曲率关系的基本概念和推导过程，并给出了实际应用案例。

通过学习本文，读者可以更加深入地理解材料力学中的弯矩曲率关系，为工程实践提供有力的支持。