土木建筑弯矩曲率关系

梁纯弯曲变形引言梁纯弯曲变形是工程力学中的一个重要概念。

在结构力学和土木工程中，梁是一种常见的结构元素，承受着各种外部荷载。

当外部荷载作用于梁上时，梁会发生变形。

本文将探讨梁在纯弯曲状态下的变形特性和相关的理论基础。

纯弯曲的概念纯弯曲是指梁所受的外部荷载仅产生弯矩作用，而不产生剪力作用。

在梁的纵轴上，上部受拉，下部受压，梁在这种状态下发生弯曲变形。

纯弯曲情况下，梁的截面仅发生弯矩引起的形状变化，并不会发生剪切变形。

纯弯曲对于大跨度的梁和悬臂梁等结构具有重要意义。

纯弯曲变形的理论基础梁纯弯曲变形的理论基础可以通过两种方法进行分析：理论分析和数值分析。

理论分析理论分析方法中，我们可以利用梁的弯矩-曲率关系来分析纯弯曲变形。

弯矩-曲率关系描述了梁截面上的弯矩和截面曲率之间的关系。

根据弯矩-曲率关系，我们可以计算出梁的曲率分布，从而得到梁的变形情况。

此外，利用材料力学中的应力-应变关系，还可以计算出梁截面上的应力分布。

数值分析数值分析方法中，我们可以使用有限元方法来模拟梁的纯弯曲变形。

有限元方法将梁划分为许多小的单元，通过求解弯矩和力的平衡方程，可以得到梁单元上的位移和应力分布。

通过将所有单元的位移组合起来，可以得到整个梁的变形情况。

纯弯曲变形的计算纯弯曲变形的计算依赖于梁的几何形状、材料特性和外部荷载。

常见的计算方法包括：基于梁理论的计算基于梁理论的计算方法适用于简单、均匀截面的梁。

在这种方法中，我们可以使用梁的截面形状和材料性质，通过弯矩-曲率关系计算出梁的曲率分布。

进一步，可以计算出梁的位移、剪力和应力等参数。

基于有限元分析的计算基于有限元分析的计算方法适用于复杂截面的梁。

在这种方法中，我们将梁划分为许多小的单元，并求解每个单元上的位移和应力分布。

通过将所有单元的位移组合起来，可以得到整个梁的变形情况。

梁纯弯曲变形的应用梁纯弯曲变形的应用广泛，特别是在土木工程和结构设计中。

通过对梁的纯弯曲变形进行分析，可以确定梁的合适截面形状和尺寸，以满足其承受的外部荷载要求。

练习1：钢筋混凝土矩形截面：b=300mm，h=600mm，h0=560mm，a s’=25mm，a s=40mm，A s’=157mm2，A s=804mm2，f y’=280MPa，f y=280MPa，E s=200GPa，E c=25.5GPa，f c=13.4MPa，f t=1.54MPa，ε0=0.002，εcu=0.0038，εs u≤10%=0.10。

.利用数值方法计算截面的M~Φ关系，并附简化计算结果M u。

2Φ10h=600mm4Φ16将程序计算出的结果导入excel生成如下表格：图1.纯弯构件截面曲率phi随弯矩M加载曲线图2.纯弯构件截面受压区高度x0随弯矩M加载曲线纯弯构件M-phi曲线数值分析程序(C++)#i#include<iostream>#include<math.h>#include<fstream>#include<iomanip>using namespace std;int main(){cout<<"设计中As=804mm2,As'=157mm2,fy=280MPa,fy'=280MPa,Es=200GPa,Ec=25.5GPa"<<endl;cout<<endl;cout<<" fc=13.4MPa,ft=1.54MPaε0=0.002，εcu=0.0038，εsu<=0.1"<<endl;cout<<endl;//给出题目的基本信息inti;double b,h,as0,as1,x0,c,t,p1,p2,p3,h0,x01,x02,d,f;double k,k1,k2,ms0,ms1,mc,f1,f2,M,sc,m1,m2,m3,mc1,e1,sc1,sc2,q;ofstreamoutfile;b=300;h=600;as0=40;as1=40;h0=h-as0;//给出题目相关参数outfile.open("data.txt");//建立数据输出文件for(mc=0.00000001;mc<=0.0038;mc=mc+0.00001){x01=0.0;x02=600.0;for(x0=0;;){x0=0.5*(x01+x02);ms1=mc/x0*(x0-25);ms0=mc/x0*(h0-x0 );//求出钢筋应变f2=200*ms1*1000;//受压区钢筋应力f1=200*ms0*1000;//受拉区钢筋应力if(f1>280){ f1=280;}if(f1<-280){f2=-280;}if(f2>280){f2=280;}//εsu<=0.1是达不到的，必定小于0.1p1=0.0;m1=0.0; p2=0.0;m2=0.0;p3=0.0;m3=0.0;for( i=0;i<=1000;i++){sc=mc*(i+0.5)/1000;if(sc<0.002){k=13.4*(1000*sc-sc*sc/0.000004);}if(sc>=0.002&&sc<=0.0038){k=13.4;}p1=p1+k*300*x0/1000;m1=m1+k*300*x0/1000*(x0*(i+0.5)/1000);}//受压区混凝土mc1=(600-x0)*mc/x0;e1=1.54/25.5/1000;//对受拉区最下缘做出判断的两个数据if(mc1<=e1)//未开裂情况下受拉区混凝土，f2受压区钢筋f1受拉区钢筋{d=600-x0;for(int j=0;j<=1000;j++){sc1=mc1*(j+0.5)/1000;k1=25.5*sc1*1000;p2=p2+k1*300*d/1000;m2=m2+k1*300*d/1000*(d*(j+0.5)/1000);}t=f1*804+p2;c=f2*157+p1;//此种情况下全结构的压力C和拉力TM=m1+f2*157*(x0-25)+m2+f1*804*(560-x0);//此种情况下的弯矩}if(mc1>=e1)//开裂情况下的受拉区混凝土，f2受压区钢筋f1受拉区钢筋{d=e1*x0/mc;for(int r=0;r<=1000;r++){sc2=e1*(r+0.5)/1000;k2=25.5*sc2*1000;p3=p3+k2*300*d/1000;m3=m3+k2*300*d/1000*(d*(r+0.5)/1000);}t=f1*804+p3;c=f2*157+p1;//此种情况下全结构的压力C和拉力TM=m1+f2*157*(x0-25)+m3+f1*804*(h0-x0);}//此种情况下的弯矩f=(c-t)/c;q=mc/x0;//f为压力和拉力之间的误差比，q为曲率if(fabs(f)<0.01){outfile<<setw(10)<<q<<endl;x0=300;break;}//输出相关数据etw(10)<<x0<< elseif(t<c)//二分法作判断，对x0做循环判断{ x02=x0;x01=x01;}else{ x01=x0;x02=x02;}}}outfile.close();system("pause");return 0;//程序结束}}。

第六章弯曲变形判断弯曲变形1、“平面弯曲梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线”2、“由于挠曲线的曲率与弯矩成正比，因此横截面的挠度与转角也与横截面的弯矩成正比”3、“只要满足线弹性条件，就可以应用挠曲线的近似微分方程”4、“两梁的抗弯刚度相同、弯矩方程相同，则两梁的挠曲线形状相同”5、“梁的挠曲线方程随弯矩方程的分段而分段，只要梁不具有中间铰，梁的挠曲线仍然是一条光滑、连续的曲线。

”6、“最大挠度处的截面转角一定为0”7、“最大弯矩处的挠度也一定是最大”8、“梁的最大挠度不一定是发生在梁的最大弯矩处。

”9、“只要材料服从虎克定律，则构件弯曲时其弯矩、转角、挠度都可以用叠加方法来求”10、“两根几何尺寸、支撑条件完全相同的静定梁，只要所受的载荷相同，则两梁所对应的截面的挠度和转角相同，而与梁的材料是否相同无关”11、“一铸铁简支梁在均布载荷的作用下，当其横截面相同且分别按图示两种情况放置时，梁同一截面的应力和变形均相同”选择弯曲变形1、圆截面的悬臂梁在自由端受集中力的作用，当梁的直径减少一半而其他条件不变时，最大正应力是原来的倍；最大挠度是原来的倍。

若梁的长度增大一倍，其他条件不变，最大弯曲正应力是原来的倍，最大挠度是原来的倍。

A：2； B：16 C：8 D：4；2、y’’=M(x)/EI在条件下成立。

A：小变形； B：材料服从虎克定律；C：挠曲线在xoy面内； D：同时满足A、B、C；3、等直梁在弯曲变形时，挠曲线最大曲率发生在处。

A：挠度最大； B：转角最大 C：剪力最大； D：弯矩最大；4、在简支梁中，对于减少弯曲变形效果最明显。

A：减小集中力P； B：减小梁的跨度；C：采用优质钢； D：提高截面的惯性矩5、板条弯成1/4圆，设梁始终处于线弹性范围内：①σ=My/I Z,②y’’=M(x)/EI Z哪一个会得到正确的计算结果？A：①正确、②正确；B：①正确、②错误； C:①错误、②正确； D：①错误、②错误；6、应用叠加原理求横截面的挠度、转角时，需要满足的条件是。

材料力学梁弯曲理论在结构概念设计中的应用随着现代建筑的快速发展，材料力学梁弯曲理论在结构概念设计中的应用已成为建筑设计的常态。

建筑结构设计是建筑工程的核心和灵魂，它是建筑工程中最重要的部分之一。

因此，在进行建筑结构设计时，必须考虑材料力学梁弯曲理论的使用，以确保建筑结构的稳定性、耐久性和安全性。

一、梁弯曲的基本原理梁是建筑结构中广泛使用的一种构件类型。

在一定的载荷作用下，梁由于其本身结构的形状和材料的力学特性，发生了弯曲。

发生弯曲时，梁的一个面（称为拉应力面）发生拉伸，另一个面（称为压应力面）发生压缩。

弯曲梁的基本原理是通过将梁内部各部分的力学行为分析，确定梁的受力状态，进而确定梁的弯曲半径和变形量等参数。

梁弯曲的基本原理可以通过材料力学梁弯曲理论来描述，其中有两个主要的方程式：弯矩-曲率定理和梁的偏差方程。

弯矩-曲率定理描述了梁曲率与弯矩之间的关系。

梁曲率是指横截面曲率半径的倒数，而弯矩是指梁上某点处的剪力矩。

弯矩-曲率定理表明，在弯矩为常数的情况下，梁的曲率和弯曲角度成反比例关系。

梁的偏差方程描述了梁在弯曲过程中的变形情况，其中涉及梁上各点的弯曲角、横向位移和变形量等参数。

梁的偏差方程是一个重要的方程式，可以用于计算梁的自由挠曲形，并确定梁的初始状态和长期状态。

二、梁弯曲理论在结构概念设计中的应用材料力学梁弯曲理论在结构概念设计中的应用主要包括以下几个方面：1. 建筑结构的初步设计在建筑结构的初步设计中，需要确定建筑结构的几何形状和梁的布置方式。

根据梁的弯曲理论，可以对建筑结构的初步设计进行评估，确定建筑结构的最大载荷和最大变形量，并根据这些数据调整建筑结构的设计方案。

2. 梁的截面设计在梁的设计过程中，需要确定梁的截面积和断面形状。

根据梁弯曲理论，可以计算出梁在最大载荷下的弯曲应力和剪应力，从而确定梁的截面大小和形状。

3. 梁的选材梁的材料选择是建筑结构设计过程中的重要环节。

根据梁的弯曲理论，可以计算出不同材料的截面尺寸，在材料强度相同的情况下，可以选择强度更高的材料，以确保建筑结构的稳定性和安全性。

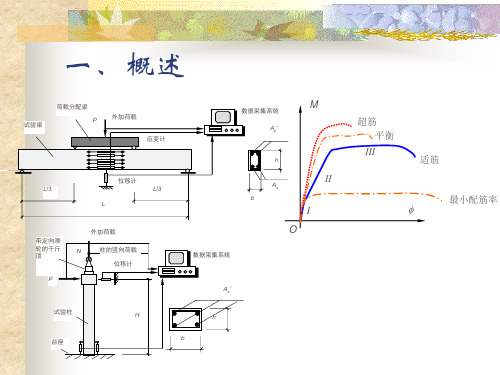
钢筋混凝土梁受弯承载力的极限状态分析一、前言钢筋混凝土梁是建筑结构中常用的梁型，其受弯承载力是设计中必须考虑的重要参数。

本文旨在通过极限状态分析的方法，深入研究钢筋混凝土梁受弯承载力的计算方法，为工程实践提供参考。

二、钢筋混凝土梁的受弯承载力钢筋混凝土梁的受弯承载力可以分为两种状态：弹性状态和破坏状态。

1.弹性状态下的计算方法在弹性状态下，钢筋混凝土梁的受弯承载力可以使用弯矩与曲率的关系式进行计算。

其中，弯矩M与截面曲率κ的关系式为：M = EIκ其中，E为混凝土的弹性模量，I为截面惯性矩，κ为曲率。

钢筋混凝土梁的受弯承载力为：N = Ws + Wc其中，Ws为钢筋的贡献，Wc为混凝土的贡献。

2.破坏状态下的计算方法在破坏状态下，钢筋混凝土梁的受弯承载力可以分为两种情况：钢筋首先达到屈服，或者混凝土首先破坏。

（1）钢筋首先达到屈服当钢筋首先达到屈服时，钢筋的贡献达到最大值。

此时，钢筋混凝土梁的受弯承载力为：N = Asfy + 0.85fcbhα其中，As为钢筋的截面面积，fy为钢筋的屈服强度，fcb为混凝土的轴心抗压强度，h为截面高度，α为中性轴深度与截面高度之比。

（2）混凝土首先破坏当混凝土首先破坏时，混凝土的贡献达到最大值。

此时，钢筋混凝土梁的受弯承载力为：N = 0.85fcbhα + βAsfy其中，β为钢筋的利用系数。

当钢筋截面面积小于等于βfcbhα/fy时，β=1，否则β按以下公式计算：β = 0.85 + 0.15fy/σs其中，σs为钢筋的应力。

三、极限状态分析极限状态分析是一种基于概率统计理论的结构设计方法，其目的是确定结构在极限状态下所能承受的荷载。

在极限状态分析中，首先需要确定荷载的概率分布，然后通过统计方法计算结构的可靠性指标，最后确定结构所能承受的荷载。

对于钢筋混凝土梁的极限状态分析，可以采用可靠度指标β进行计算。

其计算公式为：β = (R - X)/S其中，R为荷载的可靠度指标，X为结构的阈值，S为结构的标准差。

纯弯梁实验报告纯弯梁实验报告引言：纯弯梁是一种在工程结构中广泛应用的构件，在建筑、桥梁和机械等领域都有重要的作用。

本实验旨在通过对纯弯梁的力学性能进行测试和分析，探讨其在不同加载条件下的变形和破坏机理，从而对工程实践中的设计和使用提供参考。

实验设备和方法：实验中使用的设备包括纯弯梁试件、扭力加载器、应变计和数据采集系统等。

首先，将纯弯梁试件固定在试验台上，然后在试件两端施加扭力加载。

通过应变计测量试件表面的应变变化，并通过数据采集系统记录和分析数据。

实验结果与分析：1. 弯矩-曲率关系：在实验中，我们通过加载不同大小的扭矩，测量了纯弯梁试件的曲率变化。

通过绘制弯矩-曲率曲线，我们可以观察到曲率随着弯矩的增加而增加的趋势。

这表明纯弯梁试件在加载过程中会发生弯曲变形，并且变形程度与施加的弯矩大小成正比。

2. 变形模式：在实验过程中，我们还观察到了纯弯梁试件的变形模式。

随着加载扭矩的增加，试件逐渐发生弯曲，并在某一临界点处出现明显的屈曲。

在屈曲之后，试件的变形进一步增加，最终导致破坏。

这种变形模式与纯弯梁的力学性质密切相关，也是工程实践中需要考虑的重要因素。

3. 破坏机理：通过对实验数据的分析，我们可以进一步了解纯弯梁的破坏机理。

在实验中，我们观察到纯弯梁试件在屈曲之后发生了断裂，这表明试件的破坏主要是由于材料的强度不足所致。

当试件受到较大的弯矩时，其内部的应力达到或超过了材料的强度极限，导致试件发生破坏。

结论：通过本次纯弯梁实验，我们对纯弯梁的力学性能有了更深入的了解。

我们发现纯弯梁的变形和破坏与加载的扭矩大小密切相关，而且试件在屈曲之后会发生断裂。

这些结果对于工程实践中的纯弯梁设计和使用具有重要意义。

在实际应用中，我们需要合理选择材料和尺寸，以确保纯弯梁在承受设计弯矩时不发生破坏。

总结：纯弯梁作为一种常见的工程构件，其力学性能的研究对于工程实践具有重要意义。

通过本次实验，我们对纯弯梁的力学性能进行了测试和分析，探讨了其变形和破坏机理。

弯梁的弯距计算公式弯梁是一种常见的结构形式，广泛应用于建筑、桥梁、机械设备等领域。

在设计和分析弯梁结构时，弯距是一个重要的参数，它描述了弯梁在受力作用下的变形情况。

弯距的计算公式是弯梁结构分析的基础，下面我们将介绍弯梁的弯距计算公式及其应用。

弯梁的弯距是指在受力作用下，弯梁截面的中性轴发生偏移的程度。

弯距的大小直接影响着弯梁的受力性能和结构稳定性。

在工程实践中，通常采用弯矩-曲率关系来描述弯梁的受力变形情况，弯距可以通过弯矩和曲率之间的关系来计算。

弯距的计算公式可以通过梁的受力分析和变形理论推导得到。

在弯梁受力分析中，我们通常会得到梁的弯矩分布图，弯矩与曲率之间的关系可以表示为：M = E I κ。

其中，M为弯矩，E为弹性模量，I为截面惯性矩，κ为曲率。

根据弯矩-曲率关系，我们可以得到弯距与弯矩之间的关系：δ = M L / (E I)。

其中，δ为弯距，L为梁的长度。

这就是弯梁的弯距计算公式，通过这个公式我们可以计算出弯梁在受力作用下的弯距大小。

在工程实践中，弯距的计算公式可以应用于弯梁结构的设计和分析中。

通过计算弯距，我们可以评估弯梁在受力作用下的变形情况，进而确定结构的合理性和稳定性。

在设计阶段，我们可以根据弯距的计算结果来选择合适的材料和截面形式，以满足结构的受力要求。

在分析阶段，我们可以通过弯距的计算结果来评估结构的受力性能，为结构的改进和优化提供参考依据。

除了应用于弯梁结构的设计和分析中，弯距的计算公式还可以应用于结构的健康监测和故障诊断中。

通过实测弯距与计算弯距的对比，我们可以及时发现结构的变形和损伤情况，为结构的维护和修复提供科学依据。

总之，弯梁的弯距计算公式是弯梁结构分析的重要工具，它可以帮助我们理解弯梁在受力作用下的变形规律，评估结构的受力性能，指导结构的设计和分析，以及进行结构的健康监测和故障诊断。

在工程实践中，我们应该充分应用弯距的计算公式，不断完善和发展弯梁结构分析理论，为工程结构的安全可靠提供保障。

圆钢管混凝土截面轴力-弯矩-曲率关系实用计算方法丁发兴;张鹏;余志武;欧进萍【期刊名称】《哈尔滨工业大学学报》【年(卷),期】2009(041)012【摘要】为便于有限元分析,建立圆钢管混凝土压弯构件截面轴力-弯矩-曲率关系实用计算方法,基于合理的钢管混凝土数值本构模型,利用截面分层法对圆钢管混凝土压弯构件截面轴力-弯矩-曲率关系进行全过程分析,根据轴压比、钢管屈服强度、混凝土强度等级和含钢率等各主要因素对轴力-弯矩-曲率关系的影响,通过大量参数分析,分别建立圆钢管混凝土压弯构件截面轴力-弯矩相关方程实用计算公式和轴力-弯矩-曲率关系实用计算方法.通过与圆钢管混凝土压弯构件截面轴力-弯矩相关承载力和轴力-弯矩-曲率关系曲线试验结果的对比,验证该实用计算公式和实用计算方法的正确性.研究结果为圆钢管混凝土结构非线性有限元分析奠定基础.测试结果显示了方法的有效性.【总页数】5页(P133-137)【作者】丁发兴;张鹏;余志武;欧进萍【作者单位】中南大学,土木建筑学院,长沙,410075;哈尔滨工业大学,土木工程学院,哈尔滨,150090;中南大学,土木建筑学院,长沙,410075;中南大学,土木建筑学院,长沙,410075;哈尔滨工业大学,土木工程学院,哈尔滨,150090【正文语种】中文【中图分类】TU398【相关文献】1.圆钢管混凝土桥墩弯矩-曲率关系分析 [J], 臧博;朱东生;冯长友;向中富2.带轴力混凝土截面弯矩-曲率计算解析 [J], 陈旭;章胜平;鲁圣鹏;宋高丽;王春华3.带轴力混凝土截面弯矩-曲率计算解析 [J], 陈旭;章胜平;鲁圣鹏;宋高丽;王春华4.高强矩形螺旋钢筋约束高强混凝土剪力墙截面弯矩-曲率计算方法研究 [J], 赵花静;李青宁;赵珺;李书锋;郑玉5.基于ANSYS二次开发的任意截面轴力弯矩的计算方法研究 [J], 周正凡;肖明;汤福平因版权原因，仅展示原文概要，查看原文内容请购买。