迈克尔逊干涉仪测不透明薄膜厚度
- 格式:doc
- 大小:436.00 KB
- 文档页数:13

迈克尔逊干涉仪实验原理迈克尔逊干涉仪是一种利用干涉现象测量光波长、折射率、透明薄膜厚度和其他光学参数的仪器。
它由美国物理学家迈克尔逊于1881年发明,被广泛应用于精密测量和科学研究领域。
迈克尔逊干涉仪的实验原理基于干涉现象,通过光的干涉来实现精确的测量,下面我们来详细了解一下迈克尔逊干涉仪的实验原理。
首先,迈克尔逊干涉仪由光源、分束镜、反射镜、反射镜、透明样品和接收屏幕组成。
当光源发出的平行光束通过分束镜后,会被分成两束光线,一束直接射向反射镜,另一束射向透明样品。
透明样品可以是待测的物体,也可以是用来测量光波长的标准样品。
两束光线分别被反射镜反射后再次汇聚在接收屏幕上,形成干涉条纹。
其次,根据迈克尔逊干涉仪的实验原理,干涉条纹的位置与光程差有关。
光程差是指两束光线在传播过程中所经历的光程差异。
当两束光线相遇时,如果它们的光程差是波长的整数倍,就会产生明显的干涉条纹。
通过测量干涉条纹的位置,可以推导出光波长、透明样品的折射率和厚度等参数。
再次,迈克尔逊干涉仪的实验原理还可以用来测量光源的稳定性和光学元件的质量。
通过观察干涉条纹的变化,可以判断光源的频率稳定性和光学元件的表面平整度。
这对于精密测量和光学研究具有重要意义。
最后,迈克尔逊干涉仪的实验原理在科学研究和工程应用中发挥着重要作用。
它不仅可以用来测量光学参数,还可以用来研究光的波动性质和光学材料的特性。
在现代科学技术领域,迈克尔逊干涉仪被广泛应用于光学仪器的校准、精密测量和光学元件的质量检测。
总之,迈克尔逊干涉仪的实验原理基于光的干涉现象,通过测量干涉条纹的位置来实现精确的光学参数测量。
它在科学研究和工程应用中具有重要作用,为光学领域的发展做出了重要贡献。
希望本文对迈克尔逊干涉仪的实验原理有所帮助,谢谢阅读!。

光学实验中如何利用干涉原理测量薄膜厚度在光学实验中,测量薄膜厚度是一项常见且重要的任务。
利用干涉原理来实现这一测量具有高精度、非接触等优点。
接下来,让我们逐步了解这一精妙的测量方法。
干涉现象是光的波动性的一种重要表现。
当两束或多束光相遇时,它们会相互叠加,从而产生明暗相间的条纹,这就是干涉条纹。
而在测量薄膜厚度的实验中,我们常常利用的是等厚干涉原理。
等厚干涉中,一个典型的例子就是劈尖干涉。
想象一下,有一块平板玻璃,在其一端垫上一小薄片,这样就形成了一个劈尖状的空气薄层。
当一束平行光垂直入射到这个劈尖上时,在劈尖的上、下表面反射的两束光会发生干涉。
假设入射光的波长为λ,薄膜的折射率为 n。
在劈尖干涉中,相邻两条亮条纹(或暗条纹)之间对应的薄膜厚度差为λ/(2n)。
我们通过测量干涉条纹的间距以及已知的波长和薄膜折射率,就能够计算出薄膜的厚度。
为了更准确地测量薄膜厚度,实验中需要注意一些关键因素。
首先是光源的选择。
理想的光源应该具有单色性好、亮度高且稳定的特点。
常用的有激光光源,比如氦氖激光器发出的红光,其波长稳定且单色性极佳。
其次,实验装置的搭建要精确。
例如,要确保入射光垂直照射到薄膜表面,这样可以简化计算和提高测量精度。
同时,观测干涉条纹的设备也需要具备足够的分辨率,以便清晰地分辨出条纹的细节。
在实际操作中,我们可以使用显微镜来观察干涉条纹。
通过调节显微镜的焦距和位置,找到清晰的干涉条纹图像。
然后,使用测量工具(如目镜测微尺)来测量条纹的间距。
还有一种常见的干涉测量薄膜厚度的方法是牛顿环。
将一块曲率半径较大的平凸透镜放在一块平面玻璃上,在两者之间就会形成一个空气薄膜。
当平行光垂直入射时,同样会产生干涉现象,形成明暗相间的同心圆环,即牛顿环。
对于牛顿环,第 m 个暗环的半径 r 与凸透镜的曲率半径 R、入射光波长λ以及薄膜厚度 d 之间存在如下关系:r²=mλR m(m 1/2)λ² / 2 。


迈克尔逊干涉仪的原理与应用在大学物理实验中,使用的是传统迈克尔逊干涉仪,其常见的实验内容是:观察等倾干涉条纹,观察等厚干涉条纹,测量激光或钠光的波长,测量钠光的双线波长差,测量玻璃的厚度或折射率等。
由于迈克尔逊干涉仪的调节具有一定的难度,人工计数又比较枯燥,所以为了激发学生的实验兴趣,增加学生的科学知识,开阔其思路,建议在课时允许的条件下,向学生多介绍一些迈克尔逊干涉仪的应用知识。
这也是绝大多数学生的要求。
下面就向大家介绍一些利用迈克尔逊干涉仪及其原理进行的测量。
一、传统迈克尔逊干涉仪的测量应用1. 微小位移量和微振动的测量[11-14];采用迈克尔逊干涉技术,通过测量KDP晶体生长的法向速率和台阶斜率来研究其台阶生长的动力学系数、台阶自由能、溶质在边界层内的扩散特征以及激发晶体生长台阶的位错活性。
He-Ne激光器的激光通过扩束和准直后射向分束镜,参考光和物光分别由反射镜和晶体表面反射,两束光在重叠区的干涉条纹通过物镜成像,该像用摄像机和录像机进行观察和记录.滤膜用于平衡参考光和物光的强度.纳米量级位移的测量:将迈克尔逊型激光干涉测量技术应用于环规的测量中。
采用633nm稳频的He-Ne激光波长作为测量基准,采用干涉条纹计数,用静态光电显微镜作为环规端面瞄准装置,对环规进行非接触、绝对测量,配以高精度的数字细分电路,使仪器分辨力达到5nm;静态光电显微镜作为传统的瞄准定位技术在该装置中得以充分利用,使其瞄准不确定度达到30nm;精密定位技术在该装置中也得到了很好的应用,利用压电陶瓷微小变动原理,配以高精度的控制系统,使其驱动步距达到5nm。
测振结构的设计原理用半导体激光器干涉仪对微振动进行测量时,用一弹性体与被测量(力或加速度)相互作用,使之产生微位移。
将这一变化引到动镜上来,就可以在屏上得到变化的干涉条纹,对等倾干涉来讲,也就是不断产生的条纹或不断消失的条纹。
由光敏元件将条纹变化转变为光电流的变化,经过电路处理可得到微振动的振幅和频率。

迈克尔孙干涉仪测薄膜厚度实验目的:(1)了解各类型干涉条纹的形成条件,特点,变化规律及相互间的区别;(2)了解迈克耳孙干涉仪的原理,结构,掌握其调节与使用方法;(3)掌握用迈克耳孙干涉仪测量薄膜的方法。
实验仪器:迈克耳孙干涉仪,氦-氖激光器,钠光灯,白炽灯,毛玻 璃屏,薄膜等。
实验原理:测量装置及原理测量装置如图所示:由于钠光源中包含有波长相近的两种波长1λ和2λ,当平面反射d'2M 1M SL钠光G1G2G 2M A薄膜镜1M 缓慢移动时,观察屏中的条纹依次由清晰变模糊,再由模糊变清晰,条纹最模糊时,可见度最小,此时1λ光波生成亮环的地方,恰好是2λ光波生成暗环的地方,即:2211)21(2cos 2λλ+===k k d i d k (1)在1M 臂中垂直插入一折射率n 、厚度为h 的透明薄膜A ,取空气的折射率为1,1M 臂中增加的光程差∆为:)1(2-=∆n h .........(2) 插入薄膜后,条纹可见度最小的现象被破坏,继续沿原方向移动1M 平面镜d ∆的距离,直到再次出现可见度最小的现象为止,此时有: d n h ∆=-2)1(2)1(-∆=n d h ............(3) 则测出d ∆,知道折射率n ,就可计算h实验内容:(1)在迈克尔孙干涉仪换上钠光光源,可直接观察清晰的干涉条纹。
(2)慢慢旋转粗动手轮,改变d 的距离,使视场中心的视见度最小,记录1M 的位置1d 。
(3)在1M 臂中垂直插入薄片A ,可见度最小被破坏,继续沿原方向转动粗动手轮,直到再次出现可见度最小的现象,记录1M 镜的位置0d ;(4)重复(2)(3)步骤,连续测出5组数据,记录在下表中。
求出01d d d -=∆和h ,求出薄膜厚度h 的平均值。
数据记录:迈克尔孙干涉仪最小可见度0d 1d01d d d -=∆h-h注意事项:(1)迈克尔孙干涉仪是精密光学仪器,实验是严禁用手触摸各光学表面。
迈克尔逊干涉仪的使用实验报告英文回答:The Michelson interferometer is an optical instrument that uses interference to measure the speed of light, the index of refraction of a material, and the thickness of a thin film. It was invented by Albert Michelson in 1881, and it is still used today for precision measurements.The Michelson interferometer consists of two mirrors that are placed at a distance of L from each other. A beam of light is split into two beams, and each beam isreflected by one of the mirrors. The two beams are then recombined, and the interference pattern is observed. The interference pattern depends on the difference in the path lengths of the two beams.If the two mirrors are parallel, the interference pattern will be a series of bright and dark bands. The bright bands occur when the path lengths of the two beamsare equal, and the dark bands occur when the path lengths of the two beams differ by half a wavelength.The Michelson interferometer can be used to measure the speed of light by measuring the distance between the mirrors and the frequency of the light. The speed of light is equal to the product of the distance between the mirrors and the frequency of the light.The Michelson interferometer can also be used to measure the index of refraction of a material by measuring the change in the interference pattern when the material is placed in the path of one of the beams. The index of refraction of a material is equal to the ratio of the speed of light in a vacuum to the speed of light in the material.The Michelson interferometer can also be used to measure the thickness of a thin film by measuring the change in the interference pattern when the film is placed in the path of one of the beams. The thickness of the film is equal to half of the wavelength of the light multiplied by the number of bright or dark bands that shift when thefilm is placed in the path of the beam.The Michelson interferometer is a powerful tool thatcan be used to make precision measurements of a variety of physical quantities. It is a versatile instrument that has been used in a wide range of applications, including astronomy, physics, and engineering.中文回答:迈克尔逊干涉仪是一种利用干涉测量光速、材料折射率和薄膜厚度的光学仪器。
3.1.1 迈克尔孙干涉仪(本文内容选自高等教育出版社《大学物理实验》)1881年美国物理学家迈克尔孙(A.A.Michelson)为测量光速,依据分振幅产生双光束实现干涉的原理精心设计了这种干涉测量装置。
迈克尔孙和莫雷(Morey)用此一起完成了在相对论研究中有重要意义的“以太”漂移实验。
迈克尔孙干涉仪设计精巧、应用广泛,许多现代干涉仪都是由它衍生发展出来的。
本实验的目的是了解迈克尔孙干涉仪的原理、结构和调节方法,观察非定域干涉条纹,测量氦氖激光的波长,并增强对条纹可见度和时间相干性的认识。
实验原理1.迈克尔孙干涉仪的结构和原理迈克尔孙干涉仪的原理图如图3.1.1-1所示,A和B为材料、厚度完全相同的平行板,A的一面镀上半反射膜,M1、M2为平面反射镜,M2是固定的,M1和精密丝杆相连,使其可前后移动,最小读数为10-4mm,可估计到10-5mm,M1和M2后各有几个小螺丝可调节其方位。
光源S发出的光射向A板而分成(1)、(2)两束光,这两束光又经M1和M2反射,分别通过A的两表面射向观察处O,相遇而发生干涉,B作为补偿板的作用是使(1)、(2)两束光的光程差仅由M1、M2与A板的距离决定。
由此可见,这种装置使相干的两束光在相遇之前走过的路程相当长,而且其路径是互相垂直的,分的很开,这正是它的主要优点之一。
从O处向A处观察,除看到M1镜外,还可通过A的半反射膜看到M2的虚像M’2,M1与M2镜所引起的干涉,显然与M1、M’2引起的干涉等效,M1和M’2形成了空气“薄膜”,因M’2不是实物,故可方便地改变薄膜的厚度(即M1和M’2的距离),甚至可以使M1和M’2重叠和相交,在某一镜面前还可根据需要放置其他被研究的物体,这些都为其广泛的应用提供了方便。
2.点光源产生的非定域干涉一个点光源S发出的光束经干涉仪的等效薄膜表面M1和M’2反射后,相当于由两个虚光源S1、S 2发出的相干光束(图3.1.1-2)。
用迈克尔逊干涉仪测量单层薄膜的厚度和折射率实验的改进于海峰 蒋晓冬 韩厚年(淮阴工学院 淮安 223003)摘要:迈克尔逊干涉实验是大学物理实验中的一个重要实验,本文对迈克尔逊干涉仪测定薄膜的厚度和折射率实验的传统方法进行了改进,我们对原测量仪器稍做调整,提高了条纹视见度,减少了测量误差,提高了测量精度。
关键词:迈克尔逊干涉仪;光程;薄膜厚度;折射率;等厚干涉;白光干涉引言目前测量薄膜厚度和折射率的方法有多种,例如椭偏法、准波导法等等[1][2]。
其中在实验室中最常用、最简单方便的方法是利用迈克尔逊干涉方法来进行测量。
迈克尔逊干涉仪是一种典型的分振幅双光束干涉装置,可用于观察光的干涉现象,测定单色光的波长,测定光源的相干长度。
附加适当装置后,可以扩大实验范围,其中,用来测量薄膜的厚度和折射率就是其扩展实验之一。
问题提出用迈克尔逊干涉仪测薄膜的厚度和折射率, 是利用在光程差约等于零时观测白光的彩色等厚干涉条纹。
其做法是先调出白光条纹,然后将薄膜放在分光板2G 与反射镜2M 之间(薄膜与光线垂直),或薄膜贴在2M 镜上,再调出零光程差的彩色干涉条纹,反射镜移动距离d与薄透明体厚度l 、透明体折射率n 、空气折射率0n 有关系式:0()d l n n =-但是,利用上述测量单层薄膜的折射率和厚度[3][4] 的过程中存在着诸多的缺陷,首先要看到较好的等厚干涉条纹,要求单层薄膜本身较平整,以往简单的插入薄膜并不能保证薄膜的平整性,而把薄膜贴在2M 镜上,膜与镜之间也容易产生气泡,影响测量的精确性。
再者要求白光等厚干涉条纹的可观测性较强,便于测量。
本实验介绍了用迈克尔逊干涉仪方便,简单、清晰的观测等厚干涉条纹,进而用来测量单层薄膜厚度和折射率的方法。
实验原理用迈克尔逊干涉仪测单层薄膜的厚度和折射率的实验装置如图1所示。
其中反射镜M、2M和半反射镜1G、补偿板2G构成干涉仪的主1体,S为光源,A为一透光性较差的透明膜片,其所产生漫反射可以降低光源在的镜面中的反射,相对增大干涉条纹的亮度,从而增强可观测性。
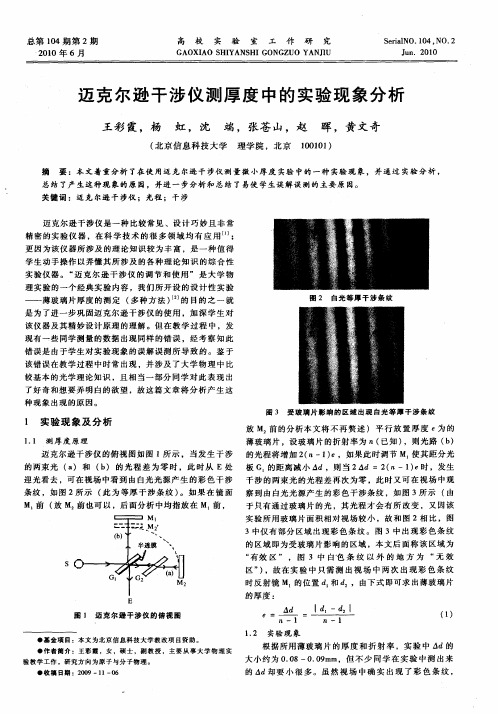
迈克尔逊干涉仪测不透明薄膜厚度摘要:为了测量不透明薄膜的厚度,借助力传感器使薄膜被等厚的空气层所代替,并运用等倾干涉的原理设计了测量装置。
此法通过间接测量,避开了机械螺旋空程差造成的影响,使用力传感器有效减小了挤压形变引起的误差。
在数据处理中,避开了传统逐差法的繁琐,而是直观地用图形对实验结果进行展示,简化和加速了分析处理数据的过程。
实测数据表明,该装置具有良好的重复性和准确性。
关键词:迈克尔逊干涉仪;力传感器;等倾干涉;数据分析目录1 测量装置及简介 (1)1.1迈克尔逊干涉仪和力传感器结构 (1)1.2实验装置介绍 (2)2 实验原理 (3)2.1 迈克尔逊光路原理 (3)2.2 等倾干涉原理 (3)2.3 简化实验数据分析原理 (5)2.4 薄膜厚度可以被等厚空气膜代替原理 (5)3 实验方法 (6)3.1 迈克尔逊干涉仪的调节 (6)3.2测定激光波长 (7)3.3测量薄膜厚度过程 (7)4 实验结果及误差分析 (7)4.1 测量数据和计算结果 (7)4.2实验误差分析 (9)5 实验改进 (9)6 结论 (10)参考文献 (10)引言薄膜的测量历来是用累积法(测一定数量的薄膜总厚度)求得的,但薄膜之间一定存在空隙使测量结果存在较大偏差。
为解决此问题,本文运用迈克尔逊干涉仪,力传感器作为辅助,巧妙地把被测薄膜厚度转换为等厚的空气膜,使得薄膜的厚度被较精确的测量出来。
厚度是薄膜的重要物理参量,越是能被精确地测量出,就越是能把握材料特性,有助于科学的进步。
本文从测量装置,原理,方法及数据误差这几方面进行讨论,并试图提出了些改进方案。
从实验结果来看,能反映出较好的精确度。
1 测量装置及简介测量薄膜厚度的理论依据是:迈克尔逊干涉仪装有蜗轮蜗杆系统,使得其具有很高的测量精度,而力传感器又能显示压力大小,有效减小操作中的挤压形变,两种仪器结合使用,使实验结果更接近于真实值。
1.1迈克尔逊干涉仪和力传感器结构1.1.1迈克尔逊干涉仪的结构迈克尔逊干涉仪的结构如图1所示,其中M1和M2是两个精密磨光的平面镜,它们放置在相互垂直的两臂上,在其背后各有三个调节螺旋,是用来调节镜面的方位的;M2固定不动,M1由精密丝杆控制,可以在臂轴上前后移动,图中11为读数窗口,由此可知M1的移动距离。
仪器前方粗动手轮(图中的13)最小分格值为10-2 mm,右侧微动手轮(图中15)的最小分度值为10-4 mm,可估读至10-5 mm,两个读数手轮构成了蜗轮蜗杆传动系统。
图中的9和10是厚薄和折射率都很均匀的相同玻璃板,9的后面涂有一层薄的银膜,光线到达此处时可以被分为强度差不多的两部分。
1.1.2力传感器结构S型压力传感器的结构如图2所示,螺纹所在的平面为受力面,安装方便,具有很高的测量精度,其稳定性能也比较好,便于控制,是理想的测力装置。
图2 力传感器结构图1.2实验装置介绍在具体测量中要把力传感器固定于迈克尔逊干涉仪导轨上,然后再接于计算机,其连接方式如图3。
计算机软件可以对作用在力传感器上的压力进行实时监测,当计算机数值为最小变化时,说明已充分接触,此时可以作为计录起点。
图3 实验主要装置简易图2 实验原理2.1 迈克尔逊光路原理迈克尔逊干涉仪的光路原理如图4 所示, 平面镜M1 、 M2 严格垂直,M1被很好的固定,M2可沿臂轴前后移动; G1 、G2 为平行等厚的光滑平玻璃板,与两平面镜成45°角,平玻璃板 G1一侧( 图靠右侧) 镀有很薄的银膜,由于可以把光束分成强度差不多的两部分,所以被称作分光板; 平玻璃板 G2 使得光束①和光束②在玻璃煤质中所走的光程相等,被称作补偿板。
光源 s 发出的光线经透镜后,射到G1的半透膜处,分成强度差不多的反射部分①和透射部分②。
光束②经 G2 射到M2后,被反射,后又经 G2 射到半透膜上,经G1反射到观察系统 P ; 光束①射到G1中的半透膜,被其反射到 M1, 继续被反射,经透射到观察屏 P ; 由于这两束光满足光的相干条件,所以在屏上相遇会形成干涉条纹。
图4 迈克尔逊光路原理图2.2 等倾干涉原理在 S 与 G1 之间加上一扩束镜,来提供不同角度的入射光,这样就可以形成等倾干涉条纹。
当 M1⊥M2 时,与镜 M1的法线和镜 M2'的法线皆成θ角的入射 力传感器 计算机迈克尔逊干涉仪光, 经 M1和M2'反射后的两束光( 1 ) 和( 2 )彼此平行(如图5),它们间的光程差可用下式表示:θcos 2d =∆ (1)其中 d 是 M1与 M2'间空气层的厚度,它们属于同一级干涉条纹,并定位于无限远。
这时,通过屏 P 观察到一组明暗相间的同心圆条纹, 其中的每一圆条纹都是等倾角光线叠加的结果, 称为等倾干涉。
中心条纹对应的倾角0=θ,对应的光程差最大,因此也是级数最高的条纹。
为了方便,可以忽略反射光线之间的相位突变,那么圆纹中心出现亮点的条件就是:λk d ==∆2 (2)由上式得中心干涉条纹的级次:λdk 2= (3)移动 M2 让 d 发生变化, 当d 增加时,对于任一级干涉条纹,例如第k 级,必定以减少其cos θk 的值来满足 2dcos θk =k λ,故该干涉条纹向θk 变大的方向移动,这时就会观察到条纹不断从中心生出向外扩展;而且只要间距d 增加2λ, 就会有一个条纹涌出。
相反,只要d 比原来小2λ, 条纹就不断缩进中心。
由此观之,每当光程差增加或减少一个波长λ时, d 就会增加或减少2λ, 也就是M2 移动了2λ 。
设变化△N 个干涉圆环动镜的移动量为 △d , 则有环数的变化△N 与 M2 的移动量△d 之间的关系为:△d =△N · 2λ ( 4 )图5 等倾干涉原理图2.3 简化实验数据分析原理迈克尔逊干涉仪测波长直接得到的是圈数N 和位置d ,对(4)式运用数学工具,对其进行不定积分处理,得d 与N 的关系为:A N d +•=2λ(5)此函数是以N 为自变量 , d 为积分变量,A 为积分常量的一条直线,对此可利用数学方法做 d-N 图(如图6), 此直线的斜率代表的正是波长的一半 , 即2λ。
由此知只要算出直线的斜率就可以轻松得出波长λ。
图6 数据分析原理图2.4 薄膜厚度可以被等厚空气膜代替原理根据式(4)知道,只要能够知道△N 个干涉环对应的动镜M2位置的移动量,就可以测得激光的波长 。
相反的如果我们知道激光的波长,动镜M2移动量又恰好等于被测薄膜的厚度,而且该厚度对应干涉环的变化数目△N 是可以被数出的,那么将各量λ,△N 带入式( 4 ) 就可测定物体的厚度。
这样就有两点说明:一是要使光程的改变正好等于被测厚度的倍数,二是要能记录与之对应干涉的吞吐环数。
为了达到第一点要求,在动镜 M2 后留一很小的空隙,然后固定一个力传感器( 如图7),再把薄膜放入该空隙,转动手轮使薄膜恰好被夹紧,此刻力传感器与 M2 的距离就是薄膜厚度。
但这时的环数还是无法读出, 为了达到第二点要求, 转动手轮使动镜M2向远离传感器方向移动,移动了多远,就有多少的环变化; 之后取出薄膜, 转动手轮使动镜 M2 向贴近传感器的方向移动, 这距离又对应了反方向的干涉环变化, 只要两次移动对应的干涉环变化数相等,M2 所在的位置就是夹有薄膜时M2的位置, 此时力传感器与 M2 之间的距离正好是薄膜厚度。
最后调手轮使M2继续靠近力传感器,直到与其距离刚好为零, 记录最后一步干涉环的变化数为△n ,这环数与膜的厚度相对应。
由(4)式知,被测的薄厚为:x =△n · 2λ (6)图7 实验光路与测量装置原理图3 实验方法3.1 迈克尔逊干涉仪的调节测量前要对迈克尔逊干涉仪进行调节,获得等倾干涉条纹后,进一步操作如下:(1) 点亮激光S ,调节激光器与迈克尔逊干涉仪的分光板G1相同高度,并且处在分光板的中心线上,使之照射加有指针的毛玻璃屏,形成均匀的扩展光源。
(2) 转动粗动手轮,使M1距G1镀膜面的距离和M2至G1镀膜面的距离基本一样,沿垂直于M1的方向观察,将看到指针的三个影子。
(3) 稍微旋转M1和M2背后的三个螺丝,使M1和M2的相对位置发生变化,达到指针双影完全重合为止,这时出现了到干涉条纹,继续调节M1的方向并前后改变M2的位置,直至干涉条纹成圆形为止。
(4) 再仔细调节M1镜下方的两个拉簧螺丝,直到干涉条纹中心到了视场中央,使干涉环中心的移动随观察者的眼睛上下左右移动,但没有条纹的“吐出”或“缩进”现象。
这时,观察到的干涉环形成严格的等倾干涉。
3.2测定激光波长有了等倾干涉条纹后,M1和M2'就达到了较好的平行,继续进行测量:(1)先将微动手轮沿某一方向旋至零,同时看着刻度轮的旋转方向,保持此方向,旋转粗动手轮,清晰的干涉圆环出现在视场中,并且读数窗口基准线对准某一刻度。
(2)慢慢地转动微动手轮,可以观察到视场中心条纹向外一个一个地涌出[1]。
待操作熟练后,记录主尺、粗动手轮和微动手轮上的初始读数,继续转动微动手轮,条纹从中心向外涌出50,100,150,200,250,300时,d的位置。
3.3测量薄膜厚度过程此时已获得严格的等倾干涉条纹,接着进行测量:(1)在动镜M2后留一空隙固定上力传感器,使动镜与测力面平行。
(2)把要测的薄膜放入空隙中,顺时针转动微动手轮使动镜M2向力传感器的方向移动,直至膜刚好被夹住。
(3)转动手轮使动镜M2向左移动,并观察干涉环周期刚好改变15圈;(4)用镊子取出薄膜;(5)向右调动镜M2使干涉环周期改变与(3)相同的圈数,此时动镜M2与测力面之间的空气层厚度正是所测薄膜的厚度;(6)继续右调动镜,直至与力传感器测力面接触,观察此步中干涉环变化了△n ;(7)将上步测得的激光波长λ及△n代人式( 6 ) ,就可计算被测薄膜厚度x 。
4 实验结果及误差分析4.1 测量数据和计算结果3 100 54.62550 0.01585 634 4150 54.64145 0.01595 638 5200 54.65739 0.01594 638 6250 54.67339 0.01600 640 7300 54.68968 0.01629 652由表一数据可计算激光的波长: nm i i 63810101==∑=λλ根据表1中的数据作d-N 图如下:图8 距离d 随N 的变化关系由图8计算得直线的斜率为 k=0.317,到激光的波长为:λ=634 nm表2 测量10次后的薄钢片数据 次数1 2 3 4 5 6 7 8 9 10 环数329 336 324 328 334 335 323 329 331 339 膜厚um 104.29 106.51 102.71 103.98 105.88 106.20 102.39 104.29 104.93 107.46由表2计算薄钢片结果为,平均厚度为 x =104.86umA 类不确定度:um n n i x x x uA 27.0)1()()(2=-=∑-[]2B 类不确定度: um x u B 18.035.03)(===λ△合成标准不确定度: um B A u u u C 32.022=+=总的厚度为: um x )32.086.104(+=4.2实验误差分析实验误差主要来源表现在下列几个方面:(1) 手动旋转微调手轮不连续、读数慢,而且每次确定环数的时候,环的大小都不会绝对一致,环数过多,人眼睛疲劳,造成人为误差。