大学物理 光栅衍射

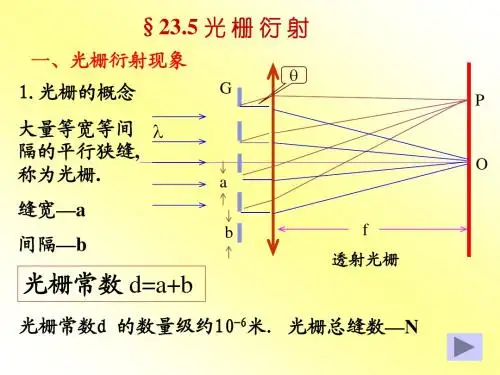
第八讲 光栅 光栅衍射第八讲 光栅 光栅衍射一、光栅衍射现象二、光栅方程三、屏上明条纹的位置四、缺级现象五、光栅光谱一、光栅衍射现象1、光栅：d反射光栅d透射光栅大量等宽等间距的平行狭缝(或反射面)构成的光学元件。

它能等宽、等距地分割入射光的波阵面d = a + b2、光栅衍射光栅衍射是多光束干涉与夫琅禾费单缝衍射的综合结果：来自不同缝的相干光的叠加是多光束干涉，而同一条缝的波阵面上各点发出的衍射光的叠加是单缝衍射。

一系列又窄又亮的明纹也叫主极大多光束干涉单缝衍射光栅衍射：受单缝衍射调制的多光束干涉。

光栅衍射sin θ0I 单I 0单-2-112(λ/a )单缝衍射光强曲线I N 2I 0单48-4-8sin θ(λ/d )单缝衍射 轮廓线光栅衍射光强曲线sin θN 24-8-48(λ/d )多光束干涉光强曲线4 4N d a ,==主极大次极大相邻主极大之间有3个暗纹，2个次级大7光栅狭缝条数越多，明纹越细亮(a)1条缝(f)20条缝(e)6条缝(c)3条缝(b)2条缝(d)5条缝二、光栅方程 0屏fxab()a b +sin θθ()sin a b θ+相邻两缝光线的光程差：= 0123()sin ,,,a b k k θλ+=ﾱﾱﾱK ，光栅方程 明纹、主极大、谱线012sin d k k ,,,θλ==ﾱﾱKoP fScreenLendλθd sin θdθ三、屏上明条纹的位置xtan x f θ=θθθtg sin ≠≠,2,1,0sin ±±==k k d ，λθ单缝衍射光强为零的位置：,3,2,1 sin ±±±=''='k k a ，λθ光栅衍射主极大（明纹）所缺级次：k ad k '=多光束干涉主极大位置：四、缺级现象,3,2,1 ,±±±='k −− k 只能取整数如果某一θ 角同时满足这两个方程，则光栅衍射中k 级主极大消失−− 缺级现象3=da λλaλ2dλ2d λ缺级缺级缺级缺级,2,1,0sin ±±==k k d ，λθ a sin k k ,,,θλﾱﾱ==ﾱﾱﾱ123，例题：用波长为λ=600nm 的单色光垂直照射光栅，观察到第二级明纹出现在sin θ =0.20处，第四级缺级。

大学物理光栅衍射光栅衍射是大学物理中的一项重要内容，它涉及到光的波动性和干涉原理。

本文将从光栅衍射的原理、实验装置、实验方法和结论等方面进行介绍。

一、光栅衍射原理光栅是一种具有周期性结构的衍射器件，它由许多平行且等距的狭缝构成。

当光通过光栅时，会产生一系列明暗相间的衍射条纹，这种现象被称为光栅衍射。

光栅衍射的原理是基于光的波动性和干涉原理。

根据波动理论，光在通过光栅时会产生衍射现象，即光波偏离了直线传播路径。

同时，由于光波的干涉作用，不同狭缝产生的光波相互叠加，形成了明暗相间的衍射条纹。

二、实验装置实验装置主要包括光源、光栅、屏幕和测量工具等。

光源通常采用激光器或汞灯等高亮度光源，以便产生足够的光强度。

光栅是一块具有许多狭缝的透明板，狭缝的数目和间距可以根据实验需要进行选择。

屏幕用于接收衍射条纹，测量工具用于测量衍射条纹的间距和亮度。

三、实验方法实验时，首先将光源、光栅和屏幕按照一定距离放置，确保光束能够照射到光栅上并产生衍射条纹。

然后，通过调整光源的角度和位置，观察衍射条纹的变化。

同时，使用测量工具对衍射条纹的间距和亮度进行测量和记录。

为了获得准确的实验结果，需要进行多次测量并取平均值。

四、结论通过实验，我们可以得出以下1、光栅衍射现象是光的波动性和干涉原理的表现。

2、衍射条纹的间距和亮度受到光源角度和位置的影响。

3、通过测量衍射条纹的间距和亮度，可以推断出光源的角度和位置。

4、光栅衍射现象在光学测量和光学通信等领域具有广泛的应用价值。

大学物理光栅衍射是一个非常重要的实验内容，它不仅有助于我们理解光的波动性和干涉原理，还可以应用于实际生产和科学研究领域。

光，这一神奇的物理现象，是我们日常生活中无处不在的存在。

当我们看到五彩斑斓的世界，欣赏着阳光下波光粼粼的湖面，或是夜空中闪烁的星光，这一切都离不开光的衍射。

在大学物理中，光的衍射是理解波动光学和深入探究光本质的关键。

我们需要理解什么是光的衍射。

实验名称：光栅衍射实验目的：1.进一步掌握调节和使用分光计的方法。

2.加深对分光计原理的理解。

3.用透射光栅测定光栅常数。

实验仪器：分光镜，平面透射光栅，低压汞灯（连镇流器）实验原理:光栅是由一组数目很多的相互平行、等宽、等间距的狭缝(或刻痕)构成的,是单缝的组合体,其示意图如图1所示。

原制光栅是用金刚石刻刀在精制的平面光学玻璃上平行刻划而成。

光栅上的刻痕起着不透光的作用,两刻痕之间相当于透光狭缝。

原制光栅价格昂贵,常用的是复制光栅和全息光栅。

图1中的为刻痕的宽度, 为狭缝间宽度, 为相邻两狭缝上相应两点之间的距离,称为光栅常数。

它是光栅基本常数之一。

光栅常数的倒数为光栅密度,即光栅的单位长度上的条纹数,如某光栅密度为1000条/毫米,即每毫米上刻有1000条刻痕。

图1光栅片示意图图2光线斜入射时衍射光路图3光栅衍射光谱示意图图4载物台当一束平行单色光垂直照射到光栅平面时，根据夫琅和费衍射理论，在各狭缝处将发生衍射，所有衍射之间又发生干涉，而这种干涉条纹是定域在无穷远处，为此在光栅后要加一个会聚透镜，在用分光计观察光栅衍射条纹时，望远镜的物镜起着会聚透镜的作用,相邻两缝对应的光程差为（1）出现明纹时需满足条件（2）（2）式称为光栅方程，其中：为单色光波长；k为明纹级数。

由（2）式光栅方程，若波长已知，并能测出波长谱线对应的衍射角，则可以求出光栅常数d 。

在=0的方向上可观察到中央极强，称为零级谱线，其它谱线，则对称地分布在零级谱线的两侧，如图3所示。

如果光源中包含几种不同波长，则同一级谱线中对不同的波长有不同的衍射角，从而在不同的位置上形成谱线，称为光栅谱线。

对于低压汞灯，它的每一级光谱中有4条谱线：紫色1=435.8nm;绿色2=546.1nm;黄色两条3=577.0nm和4=579.1nm。

衍射光栅的基本特性可用分辨本领和色散率来表征。

角色散率D（简称色散率）是两条谱线偏向角之差Δ 两者波长之差Δ 之比：（3）对光栅方程微分可有（4）由（4）式可知，光栅光谱具有如下特点：光栅常数d越小，色散率越大；高级数的光谱比低级数的光谱有较大的色散率；衍射角很小时，色散率D可看成常数，此时，Δ 与Δ 成正比，故光栅光谱称为匀排光谱。

光栅衍射实验一、实验目的：1.了解光栅的结构及光学原理；2.学会搭建实验模型；3.测左光波波长及光栅常数等。

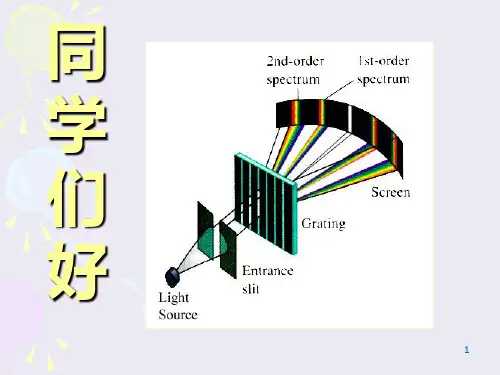
二、实验原理：光栅（grating）是大量等宽、等间距的平行狭缝（或发射而）构成的光学元件。

一般常用的光栅是在玻璃片上刻出大量平行的刻痕，刻痕为不透光部分，两刻痕之间的光滑部分可以透光（相当于狭缝）。

这种利用透射光衍射的光栅称为透射光栅。

精制的光栅，在1mm宽度内刻有数百乃至数千条刻痕。

另外一类是利用两刻痕间的反射光衍射的光柵，如在镀有金属层的表而，上刻出许多平行刻痕，两刻痕间的光滑金属面可以反射光。

这种光栅称为反射光栅（常称为闪耀光栅）。

实际应用中，各类光学设备使用的光栅基本上都是反射光栅。

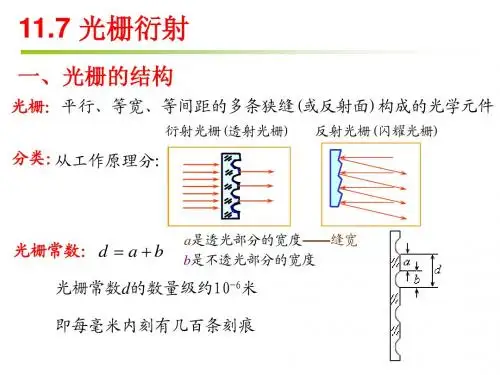
透射光栅和反射光栅的原理如图所示：I.如液单色平疔光取射金光HHW 上(图I).则览hlk 欣縫的光终丙衍射梅简％个方问俗 拓.这岐術射光级又兀相干沙・金抡收腭上久形威明塩的谱縄仙构.呂由5八心瑕定・即«/(>in^A —jiin^? )« *AS< «Af ・O 」2 .......... > ( I )此比琢为允捌力程•勻入射箱“幻U 时・间化为”“W A =止人人•尢恸力程中・"=。

・/>林勾光栩帘数：厂幻入射允波K ・X 亦炸纹级故・ 叫•足人 级明 乂纹的初姑知< mm O-从光栅力•程中町以右刘・如杲入射光不足P 色光・M1W>t 的波・KfijW/tJ V>A 也 各•平tUEJ ・「足型色Jt 将被分解・在中央位宜・K-O ・驱・0处・斤色％仍亜业住一・启・形 欣中央明纹(不级«n>- e 中央明纹刈阿対祢地分命笛AT -I ・2・$・•级允诺・各级光语堆都按波长人小的*?序依次HF 列戚一 如彩色暗绘・広歼就耙厦色•光分解力 Jtitt. (aim .3 所示.於种循團较人色敬的光宁仪為 如光赠仪箸和1W5徑分光器竹.光栅就 处册於用的分光・它能耙坯 件光分解力光带.2.反射•光冊 从透射光柵的光柵方程中可以看 到.透射光柵的零级谱线并没有分光 作用•但零级谱线的光强蜕大・因此 透射光柵的衍射谱线对能量的利用率 足很低的・造成这个现象的原因足. 光冊缝间干涉的零级极大与单经衍射 因子的主极大方向一致.光强主要樂 中在衍射主极大方向.而这个方向上 足縫间干涉的零级.无分光作用.所 以造成了光强的极大浪费.实际应用中・人们总足使用闪維光柵來分光•图4尢线入射至闪塔尢柵发生的衍射它能扱大地捉髙光的利用效皐. 反射光柵光路原理如图4所示.d 足光柵•常数：。

光栅衍射实验是大学物理实验中的一项基础实验，旨在让学生掌握光栅衍射的原理，熟悉分光计的调整与使用，以及光栅常数和光波波长的测量方法。

通过本实验，学生可以加深对光栅衍射规律的理解，为后续学习和研究光学理论奠定基础。

二、实验目的1. 熟悉分光计的调整与使用；2. 学习利用衍射光栅测定光波波长及光栅常数的原理和方法；3. 加深理解光栅衍射公式及其成立条件；4. 掌握光栅光谱的形成原理及特点；5. 熟悉光栅在光学仪器中的应用。

三、实验原理光栅是由一组数目很多的相互平行、等宽、等间距的狭缝（或刻痕）构成的，是单缝的组合体。

当一束单色光垂直照射在光栅上时，各狭缝的光线因衍射而向各方向传播，经透镜会聚相互产生干涉，并在透镜的焦平面上形成一系列明暗条纹。

光栅常数d是相邻两狭缝上相应两点之间的距离，是光栅基本常数之一。

光栅常数的倒数为光栅密度，即光栅的单位长度上的条纹数。

光栅衍射条纹的间距与光栅常数、光波波长和入射角有关。

根据光栅衍射公式，当光栅常数d、光波波长λ和入射角i确定时，衍射条纹的间距可以表示为：Δθ = λ/d其中，Δθ为衍射条纹的角间距。

四、实验仪器与设备1. 分光计：用于调节入射光的方向和测量衍射条纹的角度；2. 光栅：用于产生衍射条纹；3. 低压汞灯：提供单色光源；4. 平面镜：用于反射光；5. 望远镜：用于观察衍射条纹。

1. 将光栅放置在分光计的载物台上，调整分光计使光栅垂直于入射光；2. 调整低压汞灯，使光束垂直照射在光栅上；3. 调整望远镜，使观察者能够清晰地看到衍射条纹；4. 测量衍射条纹的角间距，计算光栅常数和光波波长；5. 改变入射角，观察光栅衍射条纹的变化。

六、实验结果与分析1. 通过实验，我们成功调整了分光计，使光束垂直照射在光栅上，并观察到清晰的衍射条纹；2. 根据光栅衍射公式，我们计算出光栅常数和光波波长，并与理论值进行了比较，误差在可接受范围内；3. 通过改变入射角，我们观察到光栅衍射条纹的变化，验证了光栅衍射公式的正确性。

大学物理实验报告光栅衍射大学物理实验报告：光栅衍射一、实验目的1、深入理解光栅衍射的原理。

2、学会使用分光计测量光栅常数。

3、观察光栅衍射现象，测定衍射光谱中各谱线的波长。

二、实验原理光栅是由大量等宽、等间距的平行狭缝所组成的光学元件。

当一束平行光垂直照射在光栅上时，每条狭缝都将产生衍射，由于各狭缝射出的衍射光之间存在光程差，它们在屏幕上叠加时会发生干涉，从而形成一系列明暗相间的条纹，称为光栅衍射条纹。

根据光栅衍射方程：＼（d\sin\theta ＝ k\lambda\）（其中＼（d\）为光栅常数，＼（＼theta\）为衍射角，＼（k\）为衍射级数，＼（＼lambda\）为入射光波长）。

当光垂直入射时，衍射角\（＼theta\）与衍射条纹的位置\（y\）之间的关系为：＼（＼tan\theta ＝＼frac{y}｛f}＼）（其中＼（f\）为望远镜的焦距）。

三、实验仪器分光计、光栅、汞灯、平面反射镜、放大镜等。

四、实验内容及步骤1、调节分光计（1）目测粗调，使望远镜、平行光管和载物台大致水平。

（2）用自准直法调节望远镜聚焦于无穷远，使望远镜能接收平行光。

（3）调节望远镜光轴与分光计中心轴垂直。

（4）调节平行光管，使其发出平行光，并使其光轴与望远镜光轴重合。

2、放置光栅将光栅放置在载物台上，使光栅平面与入射光垂直，并使光栅刻痕与载物台的平行度调节螺丝平行。

3、观察光栅衍射现象（1）打开汞灯，让平行光垂直照射在光栅上。

（2）通过望远镜观察光栅衍射光谱，注意各级谱线的分布情况。

4、测量光栅常数（1）转动望远镜，使望远镜的十字叉丝对准中央明纹（＼（k ＝0\））的中心，记录此时望远镜的读数\（＼theta_1\）。

（2）依次对准＼（k ＝＼pm1\），＼（＼pm2\）级明纹的中心，记录相应的读数\（＼theta_2\），＼（＼theta_3\），＼（＼theta_4\），＼（＼theta_5\）。

（3）根据光栅衍射方程计算光栅常数＼（d\）。