当前位置：文档之家 › 形体的三面投影图

形体的三面投影图

  • 格式：pptx
  • 大小：1.51 MB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

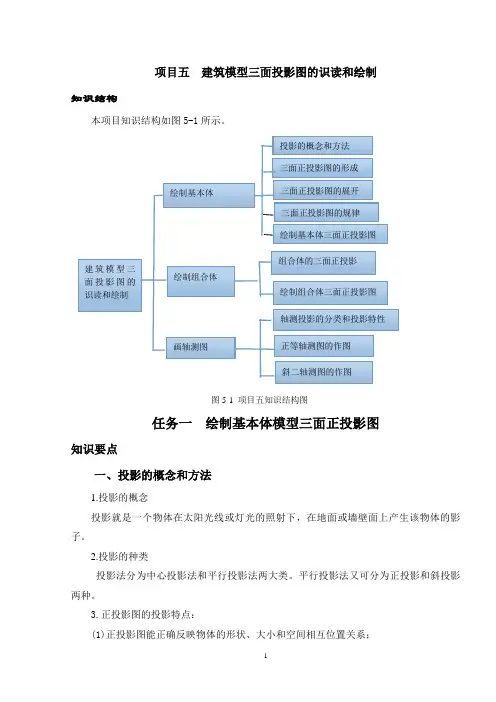
建筑识图项目五建筑模型三面投影图的识读和绘制

建筑识图项目五建筑模型三面投影图的识读和绘制

项目五建筑模型三面投影图的识读和绘制知识结构本项目知识结构如图5-1所示。

图5-1 项目五知识结构图任务一绘制基本体模型三面正投影图知识要点一、投影的概念和方法1.投影的概念投影就是一个物体在太阳光线或灯光的照射下，在地面或墙壁面上产生该物体的影子。

2.投影的种类投影法分为中心投影法和平行投影法两大类。

平行投影法又可分为正投影和斜投影两种。

3.正投影图的投影特点：(1)正投影图能正确反映物体的形状、大小和空间相互位置关系；(2)正投影图作图方便快捷；(3)正投影图的度量性好，按比例可直接量取物体的形状和大小。

正因为正投影图具有以上优点，因而在工程上应用最广泛。

绘制房屋建筑工程图主要用正投影，今后不作特别说明，“投影”即指“正投影”。

二、三面正投影图的形成1.三面正投影体系的设立在三面正投影体系中：水平放置的投影面，称为水平投影面，用H表示；正对观察者的投影面，称为正立投影面，用V表示；右面侧立的投影面，称为侧立投影面，用W表示。

这三个投影面两两相交，交线称为投影轴，其中H面与V面的交线称为OX轴；H面与W面的交线称为OY轴；V面与W面的交线称为OZ轴，且三条投影轴相互垂直的。

三个投影面或三个投影轴的交点O，称为原点。

OX轴可表示长度方向，OY轴可表示宽度方向，OZ轴可表示高度方向。

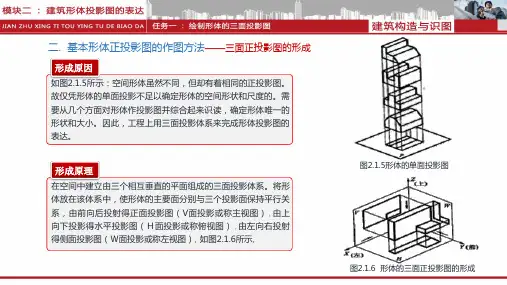
2. 三面正投影图的形成将形体安放于于H面的上方，V面的前方，W面的左侧。

自前向后作正投影，形成形体的正立面投影图或称正立投影图，简称V图；自上而下作正投影，可得形体的水平面投影图或称平面图，简称H图；自左向右作正投影，形成侧立面投影图或称侧立面图，简称W 图。

三、三面正投影图的展开1.将V面及正立面图保持不变，将H面及连同平面图绕OX轴90°，将W面及侧立面图绕OZ轴向右旋转90°，使它们和V面及正立面图处在同一个平面上。

三个正投影图展开后，三条投影轴成为十字交叉轴，OX轴、OZ轴位置不变，原OY轴则被一分为二，在H面内的为OY H；另一条在W面内的标为OY W。

第三章 基本体的三视图

第三章 基本体的三视图

例3：如图所示，已知球面对V面的转向轮廓线上点的1’ 投影，求1”、1；又知它对V的转向轮廓线上的点水平 投影2，求2’、2”。
球面转向轮廓线上点的投影的求解步骤与上一图例相 似，作图过程如图所示。
2’ 1’ 2”
y
1”
2 y
1
练 习 题
1. 根据立体图，找出相对应的三视 图，并在括号内填写相应编号。 2. 根据立体图及所给观察方向，画 出相应的三视图。 3. 根据立体图及所给观察方向，画 出相应的三视图。
1. 根据立体图找出相应三视图，并在括号内填写相应编号。









11

12
请点击解答显示其内容
2. 根据立体图及所给观察方向，画出相应的三视图。
S
请点击解答显示其内容
3. 根据立体图及所给观察方向，画出相应的三视图。
S
请点击解答显示其内容
k


k

n

n
圆的半径？
辅助圆法
k
n

例1: 已知三棱锥棱线上一点的V面投影1′和另一点 的V面投影2′，求两点的其它各面相应投影1″、1及 2、2″。
作图步骤：
y 1“ 2′ 1′ 2″ ⑴过点的V面投影1’作水平投 射线，投射线与W面相应棱线 投影的交点即为投影1”；根 据“宽一致”的投影规律， 在W面投影中量取1”的Y坐标 值，然后在H面相应棱线的投 影上直接量取Y，得H面投影1。 ⑵过点的V面投影2’分别作水 平投射线和垂直投射线，水 平投射线与W面相应棱线投影 的交点即为投影2”，垂直投 射线与H面相应棱线投影的交 点即为投影2。
作投影图时，先画出正六棱柱的水平投影正六边形，再根据 其它投影规律画出其它的两个投影。如图所示。

形体的三面正投影(基本体)

形体的三面正投影(基本体)

图3-3 4种工程形体的投影
2 棱锥
•正棱锥——底面为正 多边形，顶点过底面 中心垂线的棱锥体。
视图特征： 1)反映底面实形的视图 为多边形（三角形的组 合图形）； 2)另两视图均为三角形。
三棱锥的投影图
s
s
b
a c
c
a
b
(b)
c
s
B
a
S C A
3 棱台
•棱台可看成是由棱锥用平行于锥底面的平面截去锥顶而形 成的形体，上、下底面为各对应边相互平行的相似多边形， 侧面为梯形。
【例3.4】如图所示，已知立体表面上的点K的正面投影k'，求其 另外两面的投影k、k"。
(a) 已知条件
(b) 作图方法
【例3.5】如图所示，已知圆柱表面上线段AB的正面投影a'b'， 求其另外两面上的投影。
(a) 已知条件
(b) 作图方法
【例3.6】如图所示，已知圆锥上点K的正面投影k'，求其另两面 上的投影。
【例3.2】如图所示，已知立体表面上直线MK的正面投影m'k'， 试作直线MK的水平投影mk和侧面投影m"k"。
(a) 已知条件
(b) 作图方法
【例3.3】如图所示，已知立体表面点K的正面投影k'，试求其水 平与侧面投影k、k"。
(a) 已知条件
(b) 一般位置直线作为辅助线 求k点的投影
(c) 特殊位置直线作为辅助线 求k点的投影
视图特征： 1)反映底面实形的视图为两个相似多边形和反映侧面的 几个梯形; 2)另两视图均为梯形(或梯形的组合图形)。
2 曲面体的投影
常见的曲面体多是回转体，如圆柱、圆锥、圆球、圆环等。

CH2_三面正投影图解析

CH2_三面正投影图解析

三视图的特性
X
Z
正
高 长 宽 宽
YW
H
YH
B.立体三面投影的两面之间，存在如下关系： 正面投影和侧面投影具有相同的高度——高平齐 水平投影和正面投影具有相同的长度——长对正 重要
侧面投影和水平投影具有相同的宽度——宽相等
课堂练习：对号入座
课堂练习：对号入座
从投射线的方向观 察，不可见的投影 线用虚线表示。
圆锥体的三视图
正面投影的左、右边线 分别是圆锥最左、最右的两 条轮廓素线的投影，这两条 素线把圆柱分为前、后两半， 他们在W面上的投影与回转 轴的投影重合，在H面上的 投影与圆的水平中心线重合。 侧面投影的左、右边线 分别是圆锥最前、最后的两 条轮廓素线的投影，这两条 素线把圆柱分为左、右两半， 他们在V面上的投影与回转 轴的投影重合，在H面上的 投影与圆的竖直中心线重合。

要将几个视图联系起来看 要注意抓特征视图 要弄清视图中“线断”的 含义 要弄清视图中“线框”的 含义
形体分析法 线面分析法
W
X
O
H
Y
棱柱体的三视图
45°
棱锥体的投影特性
Z V s' S s"
在图示情况下，底面的 水平投影反映实形，正 面投影和侧面投影积聚 为水平线。
a' X
A
a H B s b
C a" c" c
W
后棱面SAC的侧面投影积 聚为一条斜线段，正面 投影和水平投影都是三 角形。 左、右两个棱面SAB、 SBC的三个投影均为三角 形。
§2.1 三面正投影图
三面正投影图是采用正投影法将空间几 何元素或几何形体分别投影到相互垂直的三 个投影面（三面投影体系）上，并按一定的 规律将投影面展开成一个平面，把获得的投 影排列在一起，使多个投影互相补充，以便 确切地、唯一地反映表达对象的空间位置或 形状。这种图又称三视图。

建筑制图与识图3立体的投影

建筑制图与识图3立体的投影
3
3.3 切割体的投影
3.3.1 平面切割体的投影
（2）棱面法——面面交线法
将平面立体上参与相交的各棱面， 与截平面求交线，这些交线即围成所 求的平面立体截交线。
3.3 切割体的投影
3.3.1 平面切割体的投影
作图步骤：
1）空间分析及投影分析 a、截平面与立体的相对位置——确定截交线的形状 b、截平面，立体表面与投影面的相对位置——确定截交线的投影特性
PV2
6′ (7′) 7 ′′
例3-8：求作被截五棱柱的三面投影图
4′ (5′) 2′ ( 3′)
PV1
1′
5′′ 3 ′′
6′′
4′′ 2′′ 1′′
3 7(5)
1
2
6(4)
3.3 切割体的投影
3.3.2 曲面切割体的投影
截交线：一般为封闭的平面曲线，特殊情况为直线。 其形状取决于曲面立体的几何特征，以及截平面与曲面立体的相对位置。
c’ （2）绘出圆柱的顶面和底面。
（3）画出正面转向轮廓线和侧面转向轮廓线。
Z
a1’ c1’(d1’) d(d1)
a(a1) c(c1)
d1’
b1’
a1”(b1”) c1’’
c’d’ b’
V a’
D
A
d” B
a”b”
c”W
C
b(b1)
圆柱的投影
正面转向轮廓线 a1’
X
c1’d1’ A1 d(d1)
da11””(b1)”c1” C1b(b1)
曲面上可见与不可见的分界线称为回转面对该投影面的转向轮 廓线，在其他投影面不应画出。
圆柱体的投影
圆柱表面由圆柱面和上下两底面所组成。圆柱面是由一直母线绕与之 平行的轴线回转而成。圆柱上任意一条平行于轴线的直母线称之为素线。

三面投影图(精)

三面投影图(精)

图2.1.8 基本形体的三面正投影图（一）图作图的实例
例 2
作出该(如图2.1.9所示（a）)有曲面形体的三面正投影图。
(a)直观图
作图步骤：
① 分析：注意，该形体中有曲面体，要掌握曲面体轮廓
线的表达方式。 ② 将形体假想的放在三面投影体系当中。放平放正。让 形体更多的面分别平行于V、H、W这三个投影面。按 习惯可先做出其在 V 面上的投影图。如图 2.1.9 （ b ） 注意该投影图中有的面反映了投影的真实性、也有的 面反映了投影的积聚性，还有的面反映了投影的类似 性。还要注意圆柱体的轮廓线的表达。 ③ 运用同样的原理再做出该形体的 H 、 W 面的投影图。 一定要注意投影图之间的对正关系（长对正、高平齐、 宽相等），同样还要注意形体轮廓图线的不可见性。
图2.1.7 三面投影图的展开
三.基本形体投影图作图的实例
例 1
作出该形体的三面正投影图，图2.1.8所示。
作图步骤：
① 将形体假想的放在三面投影体系当中。放 平放 正。让形体更多的面分别平行于V、 H、W这三个影面。按习惯可先做出其在V 面上的投影图。如图2.1.8（b）注意该投 影图中有的面反映了投影的真实性、也有 的面反映了投影的积聚性，还有的面反映 了投影的类似性。 ② 运用同样的原理再做出该形体的H 、W面 的投影图 。一定要注意投影图之间的对 正关系（长对正 、高平齐 、宽相等）， 还要注意形体轮廓图线的不可见性。
二. 基本形体正投影图的作图方法——三面正投影图的形成
形成原因
如图2.1.5所示：空间形体虽然不同，但却有着相同的正投影图。 故仅凭形体的单面投影不足以确定形体的空间形状和尺度的。需 要从几个方面对形体作投影图并综合起来识读，确定形体唯一的 形状和大小。因此，工程上用三面投影体系来完成形体投影图的 表达。

建筑制图

建筑制图
3．剖面图的画法 其步骤如下：
(1)确定剖切平面的位置
所取的剖切平面应是投影面平行面
剖切平面应尽量通过形体的孔、槽等结构的轴线或对称面 (2)画剖面剖切符号并进行标注
在投影图上的相应位置画 上剖切符号并进行编号 (3)画断面、剖开后剩余部分的轮廓线 对照右图c中的1-1剖面图和图b 中的V面投影图，可看出它们既 有共同点，又有不同点。
剖面图由两部分组成的 ： 1、是断面图形（左图b中阴影部分）；
未被切 到
断面
2、是沿投影方向未被切到但能看 到部分的投影（左图b中的杯口）。
名称
自然土壤 夯实土壤 砂、灰土 砂砾石、碎砖
三合土 石材 毛石 普通砖 饰面砖
图例
常用建筑材料图例
备注
名称
混凝土
钢筋混凝土
靠近轮廓线绘 较密的点
木材
泡沫塑料 材 料
b)平面图上的楼地 面标高符号
所注部位 的引出线
c)立面图、剖面图各 部位的标高符号
约3m m 约3mm
a)左边标注时
b)右边标注时
c)右边标注特殊情况时
d)多层标高时
3. 索引符号与详图符号
(1) 索引符号 (2) 索引剖面详图的索引符号 (3) 详图符号
(1) 索引符号
详图的编号
详图绘制在 本张图纸内
在建筑工程和装饰工程中，为了表 示楼面、屋面、墙面及地面等的构造和 所用材料，常用分层剖切的方法画出各 构造层次的剖面图，称为分层局部剖面 图。
5．旋转剖面图
用两个相交的剖切平面（交线垂直于基本投影面）剖开物体，把 两个平面剖切得到的图形，旋转到与投影面平行的位置，然后再进 行投影，这样得到的剖面图称为旋转剖面图。
第三节 断面图

02投影与基本立体三视图

02投影与基本立体三视图

反之，如果点的各个 投影均在直线的同面投 影上，则点在直线上。 在图中，C点在直线AB上，而D、E两点均不满 足上述条件，所以都不在AB直线上。
28
［例1］判断点C是否在线段AB上。
a c● b X Z a
●
c
b YW
o
a c● b YH
因c不在a b上， 故点C不在AB上。
另一判断法?
例2 三棱锥表面取点
应用简单比定理
29
二、 点分割线段成定比
V
a c C b B a c
b
X
X
b a H c
A a c
b
直线上的点分割线段之比等于其投影之比。即： AC/CB=ac/cb=ac/cb 定比定理
30
[例2] 已知直线EF 及点K 的二投影， 试判断:点K 是否在直线EF 线上。
作图步骤：
a′ d′
1）过d作de//ab，交bc于e； 2）由e 得b′c′上求出e′；
b′ e′ c′ X a d
3）又过e′作 平行于 a′b′的 辅助线； 4）由d，在辅助线上求出d′； 5）分别连接a′d ′；及 c′d′，即为所求。
b e
c
2.3 基本立体三视图
2.3.1 三视图
观察者 → 物 体 → 视 图
2.1.2 投影法的分类
投影法
投影面
形体 投射线 投射线
4
中心投影法
平行投影法
平行投影法
投影面
斜投影法
正投影法
形体
投射方向 投影(图)
投影(图)
a)斜投影法
图2.3 平行投影法
b)正投影法
5
2.1.3 正投影的基本性质

三、工程上常用的几种图示法

三、工程上常用的几种图示法

第二章投影的基本知识课外小知识：确定地面点位的方法：地面点的空间位置须由三个参数来确定，即该点在大地水准面上的投影位置（两个参数）和该点的高程。

1．地面点在大地水准面上的投影位置：地面点在大地水准面上的投影位置，可用地理坐标和平面直角坐标表示。

（1）地理坐标是用经度λ和纬度φ表示地面点在大地水准面上的投影位置，由于地理坐标是球面坐标，不便于直接进行各种计算；（2）高斯平面直角坐标利用高斯投影法建立的平面直角坐标系，称为高斯平面直角坐标系。

在广大区域内确定点的平面位置，一般采用高斯平面直角坐标。

高斯投影法是将地球划分成若干带，然后将每带投影到平面上。

本章主要介绍投影的基本概念和分类、正投影的特性以及形体三面正投影图的形成与规律；重点介绍了点、线、面的投影特征和作图方法。

知识目标：1、了解投影的基本概念和分类；2、理解正投影的特性及优缺点；3、掌握点、线、面的投影特征；4、掌握形体三面正投影图的形成；5、掌握三面投影图的规律和作图方法。

能力目标：1、能解释正投影的特性及优缺点；2、能用制图工具仪器绘制工程常见简单形体的三面正投影图；3、能使形体的三面正投影图的尺寸标注符合标准。

开章语：为了使工程构筑物表达得清晰、简洁、明了，工程图样通常应用正投影原理绘制，它是工程制图的基本方法和规律。

《道路工程制图标准》（GB 50162—92）中也规定，结构物的视图宜采用正投影法绘制。

所以，我们必须了解正投影法的投影特性，掌握绘制形体三面正投影图的方法和原理，熟悉《国标》的相关规定。

本章主要介绍了：投影的概念和分类；正投影的特性；三面正投影图的形成及其绘制；形体表面上的点、线、面的投影。

第一节投影的概念和分类一、投影的概念物体在光线的照射下，会在地面或墙面上产生影子，如图2-1-1，桥梁在阳光照射下在水面成影。

图2-1-1 桥梁在阳光下成影图2-1-2（a）是桥台模型在灯光的照射下，在纸面上产生的影子。

这种常见的自然现象，人们把它称为投影现象。

3 三面投影体系

3 三面投影体系

a
A
X
O
点A的水平投影
H
a
点的二面投影图是将空间点向二个投影面作正投影 后，将二个投影面展开在同一个面后得到的。
两面投影图的画法 V a A V a
X
ax a
O
X
ax
O
H H
a
H
展开时，规定V面不动，H面向下旋转90。用投影图 来表示空间点，其实质是在同一平面上用点在二个不同 投影面上的投影来表示点的空间位置。
1、位置关系
• 以主视图为准，俯视 图在它的正下方，左 视图在它的正右侧，
位置固定，不必标注。
2、三视图之间的“三等”关 系
• 主、俯视图长对正。
• 主、左视图高平齐。
• 俯、左视图宽相等。
2.1.3 两点的相对位置和重影 点
1.两点的相对位置
2.重影点
两点的相对位置
两点的相对位置指两 点在空间的上下、前后、 左右位置关系。
Y
① aa ⊥OX轴 aaz = aaY = XA（A到W面的距离） ② aa⊥OZ轴 aax =aa Y = ZA （ A到H面的距离）
③aax= aaz= YA
（A到V面的距离）
??已知点的两个投影，求第三投影。
解法一:
a● ax az
●
a
通过作45°线 使aaz=aax
a● 解法二:
Bb
O
a
b
Cc c
Aa
例题3：根据投影图判断点在空间的位置
b'
V
B
X a' b c' c O C
a A
例题4：画出点（15，5，10）的三面投影及空间位置
a'

4.2三面正投影图

4.2三面正投影图

4.2 三面正投影图
4.2.3 三面正投影图的展开 三个投影图位 置关系是：正立面 图在上方，平面图 在正立面图的正下 方，侧立面图在正 立面图的正右方。 用三面正投影 图表达形体的投影 时，可不画出投影 面的外框线和坐标 三面正投影图的展开 轴。
图4-6
返回
4.2 三面正投影图
4.2.4 三面正投影图的规律 展开后的三面正投影图的投影规律： (1)正立面图能反映形体正立面的形状，形体 的高度和长度，上下、左右的位置关系；平面图 能反映形体水平面的形状，形体的长度和宽度， 前后、左右的位置关系；侧立面图能反映形体侧 立面的形状，形体的宽度和高度，左右、前后的 位置关系，如下图4-7所示。
4.2 三面正投影图
4.2.1 三面投影体系 把三个相互垂直的投影面所构成的一个空间 体系称为三面投影体系，它如同房屋室内一角， 即由两面墙和地面组成，用它来得到三面正投影 图。 在三面投影体系中，处于水平位置的投影面 称为水平投影面，简称水平面或H面，正立位置投 影面称为正立投影面，简称正立面或V面，侧立位 置的投影面称为侧立投影面，简称侧立面或W面。
三面正投影图的规律
返回
4.2 三面正投影图
4.2.5 三面正投影图的作图方法 绘制三面投影图时 ，一般先绘制 V 面投影 图或 H 面投影图，然后 再绘制W面投影图。
两坡屋面房屋立体图
绘制三面正投影图 的具体方法和步骤：
(1) 在图纸上先画 出水平和垂直十字相交 线，作为投影轴，如右 图4-9a所示。 图4-9
4.2.2 三面正投影图的形成 将形体放置在三面正投影体系中，即放置在H 面的上方， V 面的前面， W 面的左方，并尽量让形 体的表面和投影面平行或垂直。 从前往后对正立投影面进行投射，在正立面 上得到正立面投影图，简称正立面图。 从上往下对水平投影面进行投射，在水平面 上得到水平面投影图，简称平面图。 从左往右对侧立投影面进行投射，在侧立面 上得到侧立面投影图，简称侧立面图。 三面正投影图的形成如下图4-5所示。

三面投影图.ppt

三面投影图.ppt
③ 运用同样的原理再做出该形体的H、W面的投影图。
一定要注意投影图之间的对正关系（长对正、高平齐、 宽相等），同样还要注意形体轮廓图线的不可见性。
(b)作形体的主视图（V面投影图） (c)作形体的俯视图（H面投影图）
(d)作形体的左视图（W面投影图）
图2.1.9 基本形体的三面正投影图（二）
图2.1.7 三面投影图的展开
三.基本形体投影图作图的实例
例1
作出该形体的三面正投影图，图2.1.8所示。
作图步骤： ① 将形体假想的放在三面投影体系当中。放
平放 正。让形体更多的面分别平行于V、 H、W这三个影面。按习惯可先做出其在V 面上的投影图。如图2.1.8（b）注意该投 影图中有的面反映了投影的真实性、也有 的面反映了投影的积聚性，还有的面反映 了投影的类似性。 ② 运用同样的原理再做出该形体的H 、W面 的投影图 。一定要注意投影图之间的对 正关系（长对正 、高平齐 、宽相等）， 还要注意形体轮廓图线的不可见性。
图2.1.8 基本形体的三面正投影图（一）
步骤1
步骤2
步骤3
三.基本形体投影图作图的实例
例2
作出该(如图2.1.9所示（a）)有曲面形体的三面正投影图。
(a)直观图
作图步骤：
① 分析：注意，该形体中有曲面体，要掌握曲面体轮廓
线的表达方式。
② 将形体假想的放在三面投影体系当中。放平放正。让
形体更多的面分别平行于V、H、W这三个投影面。按 习惯可先做出其在V面上的投影图。如图2.1.9（b） 注意该投影图中有的面反映了投影的真实性、也有的 面反映了投影的积聚性，还有的面反映了投影的类似 性。还要注意圆柱体的轮廓线的表达。
形成原理
在空间中建立由三个相互垂直的平面组成的三面投影体系。将形 体放在该体系中，使形体的主要面分别与三个投影面保持平行关 系，由前向后投射得正面投影图（V面投影或称主视图），由上 向下投影得水平投影图（Ｈ面投影或称俯视图），由左向右投射 得侧面投影图（Ｗ面投影或称左视图）。如图2.1.6所示。

工程制图 三视图

工程制图 三视图

k


k
圆的半径？
k
辅助圆法
3.3 简单叠加体的三视图
一、简单叠加体的叠加形式及表面过渡关系
⒈ 回转体与回转体叠加
⒉ 回转体与平面体叠加 形体之间 一般有轮廓线 分界
⒊ 平面体与平面体叠加
有实线 有实线
有虚线
无线
两体表面共面时，中间无分界线。
二、简单叠加体的画图方法
例：画出所给叠加体的三视图。 ⑴ 分解形体，弄清它们的叠加方式。
立板 肋板

底板和立板右侧面共面叠加 肋板与底板和立板前后对称叠加
底板
⑵ 逐块画三视图并分析表面过渡关系。
①底板 ②立板 ③肋板 看得见的线画实线 看不见的线画虚线
表面共面， 应无线。
⑶ 检查、加深。
三、简单叠加体的读图方法
⒈ 弄清视图中图线的意义 ① 面的投影 ② 面与面的交线 ③ 回转面轮廓素线 的投影
二、简单叠加体的画图和看图方法
⒈ 画图时一定逐个形体画，同时注意分析表面的 过渡关系，以避免多线或漏线。 ⒉ 看图时切忌只抓住一个视图不放。利用封闭线 框分解形体和分析表面的相对位置关系。
⑵ 棱柱的三视图 在图示位置时，六棱柱 ⑶ 棱柱面上取点
a
(
a b)


b
b
a
2.棱锥 ⑴ 棱锥的组成
由一个底面和若干 侧棱面组成。侧棱线交 A 于有限远的一点——锥 顶。
S
C B
k
a a
ห้องสมุดไป่ตู้
s
s
⑵ 棱锥的三视图
棱锥处于图示位置 ⑶ 在棱锥面上取点 时，其底面ABC是水平 面，在俯视图上反映实 同样采用平面上取 形。侧棱面SAC为侧垂 点法。 面，另两个侧棱面为一 般位置平面。

三讲基本体三面投影

三讲基本体三面投影

截交线的性质：
⒈ 是一封闭的平面多边形。
⒉ 截交线的形状取决于被截立 体的形状及截平面与立体的 相对位置。 截交线的投影的形状取决于 截平面与投影面的相对位置。
⒊ 截交线是截平面与立体表面 的共有线。
一、平面体表面的截交线
• 截交线是一个由直线组成的封闭的平 面多边形。
• 截交线的每条边是截平面与棱面的交线。
V a’
D
A
正面转向轮廓线
d”
B
a”b”
c”W
C
a
b
c
圆柱的投影
a’ c’d’ 侧面转向轮廓线 A
d
X
a
d” a”b” c”
Cb
c
Y
2、圆柱表面上取点
已知圆柱表面上的点M及N正面投影a’、 b’、m′ 和n′，求它们的其余两投影。
b’ a’
(b”) a”
b
a
在圆柱表面上取点
二、圆锥体
1、 圆锥的投影
c’d’
M
A d
m
a
d” m” Ba”(b”) C b c
c”
Y
圆锥的三面投影图
s’
s”
已知圆锥表面的点
M的正面投影m’,求出
M点的其它投影。
m’ a’
1’ c’(d’) d
m”
b’
过m’s’作圆锥表面
d” a’(b’)1” c” 上的素线，延长交底
圆为1’。
a
s
b
m
1 c
图3-14 圆锥的投影及表面上的点
c
Y
图3-11 圆锥的三面投影图
圆锥投影图的绘制：
s’
s”
（1） 先绘出圆锥的对 称线、回转轴线。

第五讲第4章立体投影(一)

第五讲第4章立体投影(一)

第五讲第4章立体的投影（一）本讲的学习目标：掌握平面立体（棱柱、棱锥）的形状特点，掌握曲面立体（圆柱、圆锥、圆球）的形成原理；熟练掌握基本形体的投影特征以及形体表面上点和线的求解方法。

学习的重点：基本形体的投影特征以及形体表面上点和线的求解方法4.1 平面立体的投影图4-1 房屋形体的分析图4-2 水塔形体的分析基本形体：组成形体的最简单但又规则的几何体，叫做基本形体。

基本形体的分类：根据表面的组成情况，基本形体可分为平面立体和曲面立体两种。

平面立体：表面由若干平面围成的基本体，叫做平面立体。

平面立体类型：有棱柱、棱锥、棱台等。

平面体的投影：作平面立体的投影，就是作出组成平面立体的各平面的投影。

4.1.1 棱柱4.1.1.1 棱柱的投影如图4-3所示，有两个三角形平面互相平行，其余各平面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些平面所围成的基本体称为棱柱。

图4-3 三棱柱体当底面为三角形、四边形、五边形……时，所组成的棱柱分别为三棱柱、四棱柱、五棱柱等。

（a）立体图（b）投影图图4-4 三棱柱的三面投影分析其三面投影图：W投影：投影为三角形。

H投影：投影为两个矩形。

V投影：投影为一个矩形。

4.1.1.2 棱柱表面定点和定线【例4-1】如图4-5所示，已知三棱柱上直线AB、BC的V投影，求另外两个投影。

（a）已知条件（b）作图图4-5 三棱柱表面上的点和线【例4-2】如图4-5所示，已知四棱柱表面上点K的V投影和点M的V投影，求它们的另外两投影。

（a）立体图（b）已知条件（c）作图图4-6 四棱柱表面上的点4.1.2 棱锥定义：由一个多边形平面与多个有公共顶点的三角形平面所围成的几何体称为棱锥。

如图4-6所示为三棱锥。

图4-7-1 三棱锥根据不同形状的底面，棱锥有三棱锥、四棱锥和五棱锥等。

当棱锥底面为正n边形时，称为正n棱锥。

4.1.2.1 棱锥的投影1. 棱锥如图4-7所示为一正三棱锥,三棱锥底面ABC是水平面，后棱面SAC是侧垂面，其它两个侧面都是一般面；棱线SB为侧平线，其它两条棱线为一般线。

三视图投影性质及画法

三视图投影性质及画法

(一) 回转体的形成方法
名称 圆 锥 体
圆柱体
圆球体
圆环体
回 转 面 形 成
直母线绕和 它相交的轴线回 转而成圆锥面
O S
直母线绕和 它平行的轴线回 转而成圆柱面
O
A
圆母线绕以 它的直径为轴线 回转而成圆球面
O
圆母线绕和 它的共面但不过 圆心的轴线回转 而成圆环面
O
方
法
和
简
图
A
O
A1 O
O
O
形体 由圆锥面和一个圆 由圆柱面和两个圆 由圆球面围成的 由圆环面围成的
o'
o”
o
以底面对称中心作为坐标原点
二、平面立体及其表面上的点和线
(三) 平面立体的画法
棱线的可见投影画成粗实线，棱线的不可见投影画成细虚线。
注意：
s'
s”
1.所有投影的边缘轮 廓线都是可见的，要用粗 实线画出。
a'
1' c' 2'
2.边缘轮廓线内直线
c
b' s
的可见性，要利用交叉两
1(2)
直线上的重影点来判断。 a
各点投影符合 三面投影特性
俯视图：从上向下做正投射得到的图形。 左视图：从左向右做正投射得到的图形。
§7-1 立体及其表面上的点和线
一、立体的三视图及其投影规律
(一) 三棱锥的三视图
Z
V
s'
s”
a' b'
c'
a”
X
O (c”)
a
sc
b
b” Y
投影过程： (1)建立坐标系; (2)作正投影; (3)投影面展开;

高校高等职业教育《建筑工程制图与识图》教学课件 第3章 基本体的投影

高校高等职业教育《建筑工程制图与识图》教学课件 第3章 基本体的投影

§3.3
3.3.1平面体的截交线
截割体的投影
由于平面体是由平面围成，所以平面体的截交线是封闭的平面折线， 即平面多边形。
求平面立体截交线的步骤：
（1）分析 截交线形状及投影形状； （2）求点 利用截平面的积聚性求棱线与截平面的交点； （3）连线 按一定顺序并根据可见性连线。
§3.3 截割体的投影
圆锥与各种平面立体的相贯线; ➢ 用辅助平面法可求: 圆球与各种平面立体的相贯线。
圆环与各种平面立体的相贯线。
§3.4 相贯体的投影
[例题15] 已知圆柱体与四棱柱相贯的俯视图,补全V、W面投影。
易多线 1’
2’
解题步骤：
1’’(2’’)
3’(5’)
4’(6’)
5’’(6’’)
3’’(4’’)
二、圆锥
投影分析和画法 圆锥的底圆平面为水平面，其
水平投影为圆，且反映实形； 正面投影和侧面投影均积聚为
直线段，长度等于底圆的直径。
投影特点： 一个视图为圆，另两个为三角形。
§3.2
二、圆锥
圆锥表面上取点:
回转体的投影
素线法取点
§3.2
二、圆锥
圆锥表面上取点:
回转体的投影
纬圆法取点
四、圆环
圆环的三视图：
回转体的投影
§3.2
四、圆环
圆环表面取点：
已知圆环面上的 点A、B 的一个 投影，求它们的 另一个投影
回转体的投影
§3.2
四、圆环
回转体的投影
圆环表面取曲线：
已知圆环面上的 曲线AD 水平投 影，求正面投影
§3.1 基本体的投影
[例题3] 补全属于基本回转体表面的点和线段的三面投影。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

5、长、宽、高和方位关系
上
左 右 后 下
上
前
下 后
左 前 右
随堂练习-1
想一想：如图所示蒙古包，小明认为这个
蒙古包可以看成下图所示几何体，并画出了 这个几何体的三视图，你同意小明的做法吗？ 为什么？
主视图
左视图
俯视图
随堂练习-3
找出图中每一物品所对应的主视图：
小结
拓展
• 三视图形成
• 主视图——从前向后投影得到的图 • 俯视图——从上向下投影得到的图 • 左视图——从左向右投影得到的图
V
由前向后投影 主视图： 由上向下投影 俯视图 由左向右投影 左视图
H
W
X
图2
Y
3、三面投影体系的展开
Z V 主视图 X 左视图 YW W
O
俯视图
H YH 图3
4. 三视图的投影规律
主视图视图长对正； 主、左视图高平齐； 俯、左视图宽相等。
俯视图
长对正
45°
宽相等
YW
YH
形体的 三面投影图
主讲老师：李晓丹 交通信息系
旧知回顾
什么是平行正投影法？
物体 投射线
投射线相互平行 且垂直于投影面
900
H
引 入
仅有一个投影面不能够 确定形体的空间形状。
如何解决？
单面正投影
形体的三视图
1、三面投影体系的建立
正立投影面
Z
侧立投影面
V
W
X
H
0
水平投影面
Y
图1
2、三视图的形成
Z
• 画物体的三视图时,应遵循的投影规律:
长对正,高平齐,宽相等.
• 挑战“自我”,提高画三视图的能力
拓展训练
画出圆台的三视图
主视图 主视图 左视图 左视图
俯 视 图
谢谢！